رگرسیون خطی Linear Regression در نرمافزار SPSS
توضیحات مدل رگرسیون خطی برگرفته شده از کتاب روش های پیشرفته آماری و کاربردهای آن
در مباحث مربوط به همبستگی (لینک آنها را میتوانید از اینجا مشاهده کنید) درباره ارتباط و تأثیرپذیری دو کمیت بر روی یکدیگر صحبت کردیم و این ارتباط را به صورت یک اندازه عددی و تحت مفهوم ضریب همبستگی بیان کردیم.
یکی از بزرگترین محدودیت آنالیزهای ضریب همبستگی عدم قابلیت پیشبینی آنها و تعمیم دادن نتایج حاصل از آن به سایر حالتهای مشابه میباشد. علاوه بر آنکه ضریب همبستگی تنها به بیان ارتباط میان دو کمیت میپردازد، به همین دلیل نیاز به ایجاد و استفاده از یک ابزار مفیدتر آماری احساس میشود.
مطالعه پیرامون ماهیت رابطه بین کمیتها را تحلیل رگرسیون Regression Analysis میگوییم. در واقع دو هدف عمده از بررسی روابط میان کمیتها عبارت است از
-
- چگونگی رابطه و میزان تاثیر کمیتها بر روی یکدیگر را مطالعه میکنیم.
- با در اختیار داشتن مقدار برخی از کمیتها، به پیشبینی بقیه کمیتها میپردازیم.
- فرض صفر. معادله و مدل رگرسیونی ایجاد شده مناسب نیست. به معنای اینکه بین X ها و Y رابطه خطی وجود ندارد.
- فرض مقابل. معادله و مدل رگرسیونی ایجاد شده مناسب است. یعنی حداقل بین یکی از X ها و Y رابطه خطی وجود دارد.
- Unstandardized Coefficients (B & Std. Error)
- Standardized Coefficients (Beta)
- t
- Sig
- Confidence Interval for B 95.0%
- Correlations
برخلاف اندازههای عددی انواع مختلف ضرایب همبستگی که تنها دربارهی چگونگی رابطه و میزان تاثیر کمیتها بر روی یکدیگر بحث میکند، رگرسیون به ما این امکان را میبخشد که بتوانیم به هدف مهم قابلیت پیشبینی نیز دست یابیم.
چنانچه علاقمند هستید، مطالب بیشتری دربارهی رگرسیون و تئوریهای آن بدانید، به شما پیشنهاد کتاب روشهای پیشرفته آماری و کاربردهای آن – فصل هشتم را میدهم. با این حال من در این مقاله به دنبال آموزش رگرسیون خطی با استفاده از نرمافزار SPSS هستم. بنابراین از مطالب نظری صرفنظر میکردم و به مباحث کار با نرمافزار میپردازم.
چنانچه علاقمند بودید میتوانید در این لینک پیش فرضهای تحلیل رگرسیون خطی را مشاهده کنید.
مثال رگرسیون خطیExample
به دادههای این مثال که مربوط به متوسط آلودگی هوا در فصل پاییز برحسب واحد PSI در 21 شهر کشور است، توجه کنید. فایل دیتا این مقاله را میتوانید از اینجا Linear Regression with SPSS دریافت کنید.
در این بررسی چند عامل موثر در آلودگی هوای این شهرها مورد مطالعه قرار گرفته است. عواملی که مورد بررسی قرار گرفتهاند عبارتند از تعداد کارخانههای بزرگ (بیشتر از 25 کارگر)، کارخانههای کوچک (کمتر از 25 کارگر)، تعداد وسایل نقلیه و وضعیت سیستم حمل و نقل عمومی در این 21 شهر. به طور حتم عوامل تاثیرگذار دیگری نیز بر روی آلودگی هوا، وجود دارند. با اینحال ما بررسی خود را بر روی این چند عامل انجام دادهایم.
در پی آن هستیم که مدل رگرسیون خطی زیر را به دادهها برازش دهیم.
$ \displaystyle y={{b}_{0}}+{{b}_{1}}{{x}_{1}}+{{b}_{2}}{{x}_{2}}+{{b}_{3}}{{x}_{3}}+{{b}_{4}}{{x}_{4}}$
که در آن $ \displaystyle y$ میزان آلودگی هوا، $ \displaystyle {{x}_{1}}$ تعداد کارخانههای، $ \displaystyle {{x}_{2}}$ تعداد کارخانههای کوچک، $ \displaystyle {{x}_{3}}$ تعداد وسایل نقلیه و $ \displaystyle {{x}_{4}}$ به عنوان یک کمیت کیفی عددی بین 1 تا 6 میباشد (عدد بیشتر بهتر بودن وضعیت سیستم حمل و نقل عمومی آن شهر را نشان میدهد). همانگونه که مشاهده میکنید علاوه بر کمیتهای کمی در مدلهای رگرسیونی میتوان از کمیتهای کیفی نیز استفاده کرد.
ما در این مطالعه به دنبال تعیین میزان تاثیر هر یک از این عوامل بر روی شاخص آلودگی هوا و ساختن مدلی جهت پیشبینی آینده هستیم. در تصویر زیر بخشی از فایل دیتا را مشاهده میکنید.
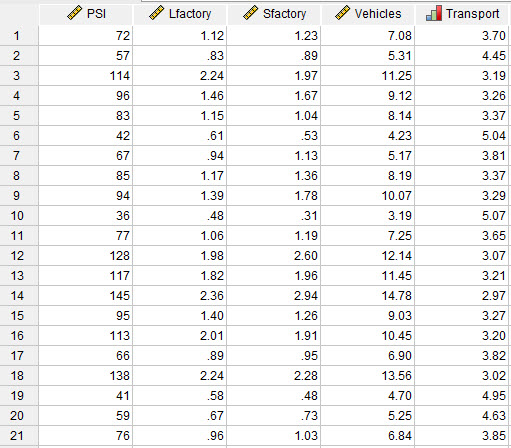
دادههای مثال تحلیل رگرسیون خطی با SPSS به منظور یافتن مدل رگرسیون خطی در نرمافزار SPSS از مسیر زیر استفاده میکنیم.
Analyze → Regression → Linear
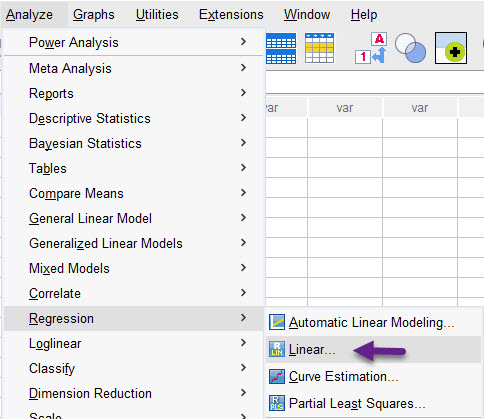
مسیر انجام رگرسیون خطی در نرمافزار SPSS تنظیمات نرمافزارSetting
هنگامی که به مسیر بالا در نرمافزار SPSS میرویم، پنجره زیر با نام Linear Regression برای ما باز میشود.
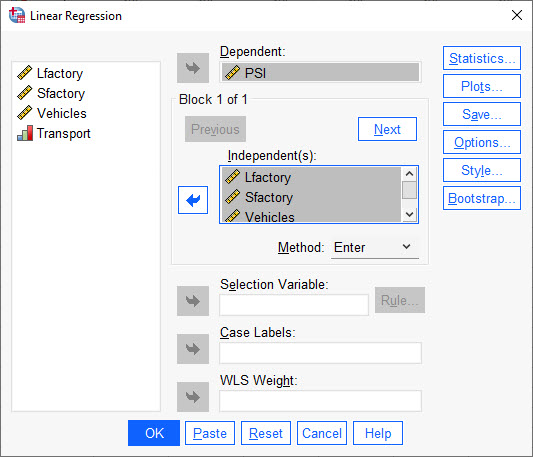
پنجره Linear Regression از آنجا که به دنبال پیشبینی میزان آلودگی هوا هستیم، آلودگی بر حسب PSI به عنوان کمیت وابسته Dependent و کمیتهای تعداد وسایل نقلیه، کارخانههای بزرگ، کارخانههای کوچک و وضعیت سیستم حمل و نقل عمومی، به عنوان کمیتهای مستقل Independent تعریف میشوند.
در پنجره Linear Regression تبها و گزینههای مختلفی وجود دارد که من سعی میکنم به بیان مهمترین آنها بپردازم.
Statistics
در تب
 میتوانیم آمارهها و یافتههای مختلفی جهت بررسی مناسب بودن مدل رگرسیونی برازش شده و پارامترهای براورد شده، به دست بیاوریم. در تصویر زیر میتوانید آنها را ببینید.
میتوانیم آمارهها و یافتههای مختلفی جهت بررسی مناسب بودن مدل رگرسیونی برازش شده و پارامترهای براورد شده، به دست بیاوریم. در تصویر زیر میتوانید آنها را ببینید.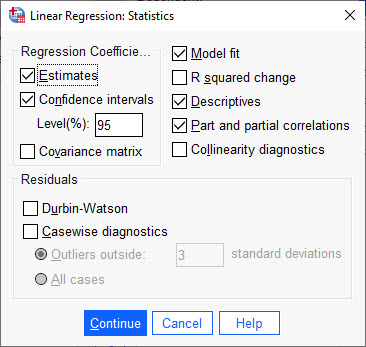
تنظیمات تب Statistics در مدل رگرسیون خطی من در تب Statistics گزینههای مربوط به براورد پارامترها (Estimates) و یافتن فواصل اطمینان 95 درصد (Confidence intervals) آنها را انتخاب کردهام.
به دست آوردن آمارههایی جهت بررسی مناسب بودن مدل رگرسیونی (Model fit)، آمارههای توصیفی از کمیتها (Descriptives)، ضرایب همبستگی پیرسن و جزئی بین هر X با کمیت وابسته (Part and partial correlations)، گزینههایی است که من انتخاب کردهام.
علاقمند بودید دربارهی تشخیص هم خطی (Collinearity diagnostics) در این لینک (تشخیص هم خطی Collinearity Diagnostics در مدل های رگرسیونی) مطالب بیشتری ببینید.
من همچنین دربارهی آمارههای مربوط به باقیماندهها Residuals یعنی دوربین واتسن Durbin-Watson و تشخیص موردی Casewise diagnostics توضیحات و مطالبی نوشتهام. علاقمند بودید، آن را بخوانید. (آزمون دوربین واتسن Durbin-Watson و تشخیص موردی Casewise diagnostics)
Plots
ما از شاخصها و اندازههای عددی به منظور سنجش مناسبت مدل رگرسیونی استفاده میکنیم. همچنین میتوانیم از نمودارهای آماری برای انجام این کار، استفاده کنیم. در این بخش نمودارهایی که از طریق آنها میتوان خوب بودن مدل را بررسی کرد. وجود دارد.
برای رسم اینگونه نمودارها از تب Plot
 استفاده میکنیم. در تصویر زیر آن را ببینید.
استفاده میکنیم. در تصویر زیر آن را ببینید.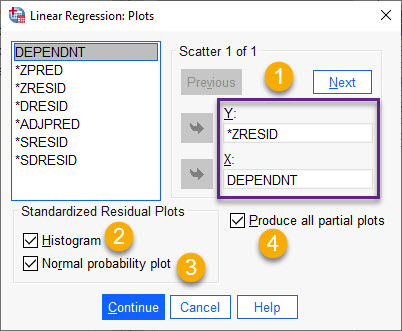
تب Plot برای رسم نمودار در رگرسیون خطی من بخشهای مختلف تصویر بالا را شمارهگزاری کردهام. در ادامه به توضیح آنها میپردازم.
1- نمودار باقیماندههای استاندارد شده (ZRESID) در برابر کمیت وابسته (Dependent)
از نمودارهای مناسب برای نشان دادن معنادار بودن مدل رگرسیونی و مناسب بودن تابع رگرسیونی در برازش دادهها، نمودار پراکنش کمیت پاسخ و مقادیر باقیماندههای نرمالشده است. اگر نقاط این نمودار به صورت پراکنده و به دور از نظم و قاعدهای در اطراف خط صفر پخش شده باشند، نشان میدهد مدل به دست آمده مناسب است.
2- هیستوگرام (Histogram) باقیماندههای استاندارد شده Standardized Residual به منظور مشاهده نحوه فراوانی آنها مفید است. همانگونه که میدانیم یکی از پیشفرضهای انجام تحلیل رگرسیون خطی، نرمال بودن توزیع باقیماندهها است. با استفاده از این هیستوگرام میتوانیم منحنی نرمال باقیماندهها را مشاهده کنیم.
3- نمودار احتمال نرمال (Normal Probability Plot)
یکی از مهمترین تئوریهای مناسب بودن مدل رگرسیون خطی، نرمال بودن باقیماندههای آن است. ما از طریق رسم نمودار Normal Probability Plot میتوانیم به صورت شهودی درکی از نرمال بودن مقادیر باقیمانده داشته باشیم. در این نمودار، هر باقیمانده در مقابل ارزش مورد انتظارش هنگامی که توزیع دادههای باقیمانده نرمال است، رسم میشود. هر چه نقاط نمودار به خط نیمساز نزدیکتر باشند، تبعیت باقیماندهها از توزیع نرمال بیشتر است. اگر نمودار از خط نیمساز انحراف جدی داشته باشد، نتیجه میشود که توزیع باقیماندهها نرمال نیست. در این زمینه علاقمند بودید، این لینک را ببینید. (نمودار احتمال نرمال Normal Probability Plot در مدل های رگرسیونی)
4- نمودارهای رگرسیون جزئی (Partial Regression Plots)
نمودارهای رگرسیون جزئی معمولاً برای شناسایی نقاط اثرگزار Influential Data استفاده می شوند. با استفاده از آنها میتوان اثر افزودن یک کمیت اضافی به مدل را نشان داد، با توجه به اینکه یک یا چند کمیت مستقل دیگر از قبل در مدل وجود دارند. من در این لینک دربارهی این نمودارها بیشتر توضیح دادهام. (گرافهای رگرسیون جزئی در تحلیلهای رگرسیون خطی)
من در تب Plots گزینههای بالا را انتخاب کردهام. هنگام به دست آوردن نتایج و خروجیهای نرمافزار در ادامه بیشتر دربارهی آنها صحبت میکنیم.
Save
تب دیگر در پنجره Linear Regression با نام
 قرار دارد. ما با استفاده از گزینههای این تب میتوانیم، خروجیهای بیشتری از نتایج خود داشته باشیم. اغلب این خروجیها در پنجره دیتا نرمافزار SPSS قرار میگیرند. در تصویر زیر آن را ببینید.
قرار دارد. ما با استفاده از گزینههای این تب میتوانیم، خروجیهای بیشتری از نتایج خود داشته باشیم. اغلب این خروجیها در پنجره دیتا نرمافزار SPSS قرار میگیرند. در تصویر زیر آن را ببینید.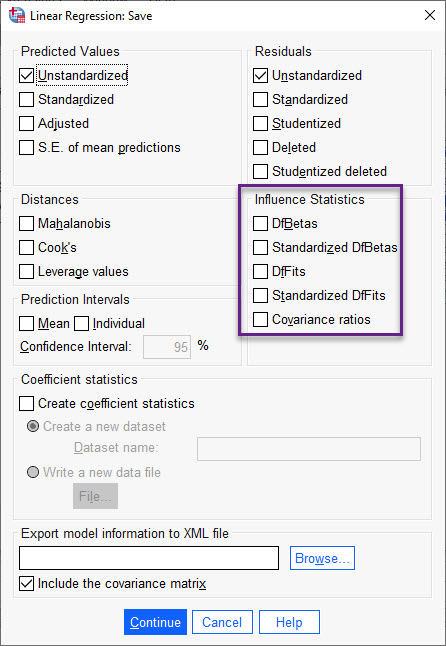
تب Save در تحلیل رگرسیون خطی با SPSS من در این پنجره از نرمافزار خواستهام مقادیر پیشبینی شده Predicted Values و باقیماندههای Residuals مدل رگرسیونی را برای ما نشان دهد. البته من حالت غیراستاندارد شده Unstandardized را انتخاب کردهام. به سادگی میتوانستیم گزینه استاندارد شده Standardized را نیز انتخاب کنیم.
من در پنجره بالا دور کادر Influence Statistics نیز خط کشیدهام. از گزینههای این کادر به منظور بررسی و به دست آوردن دادههای اثرگزار استفاده میشود. در لینک (یافتن نقاط تاثیرگذار یا دادههای موثر Influence Statistics در تحلیل رگرسیونی)، در این موضوع توضیح دادهام. علاقمند بودید آن را بخوانید.
Options
بر روی تب
 بزنید تا پنجره زیر برایتان باز شود.
بزنید تا پنجره زیر برایتان باز شود.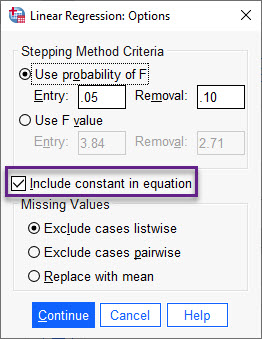
تب Options در مدل رگرسیون خطی نرم افزار SPSS به صورت پیش فرض گزینه Include constant in equation را انتخاب کرده است. با انجام این کار، مدل رگرسیونی شامل ضریب ثابت نیز خواهد بود. معمولاً این کار را توصیه میکنیم. Continue کنید تا به پنجره اصلی Linear Regression برگردید.
در پنجره Linear Regression و بخش Method میتوانید انواع روشهای ورود کمیتهای مستقل (یعنی همان Xها) را مشاهده و انتخاب کنید.
روشهای ورود X ها به مدل من در این لینک (انتخاب روشهای ورود کمیتهای مستقل به مدل رگرسیونی)، در این زمینه بیشتر توضیح دادهام. در این مثال همان روش پیشفرض یعنی Enter انتخاب شده است.
چنانچه بخواهیم تحلیل رگرسیون خطی فقط بر روی محدوده و یا اعداد خاصی از یک Variable انجام شود، میتوانیم از کادر Selection Variable استفاده کنیم. علاقمند بودید در این زمینه، لینک (Selection Variable در مدل های رگرسیونی) را ببینید.
خب، حال OK میکنیم تا بتوانیم به بیان و توضیح نتایج و خروجیهای نرمافزار SPSS در تحلیل رگرسیون خطی بپردازیم.
نتایج تحلیل رگرسیون خطیOutput & Results
در ابتدای نتایج و خروجیهای نرمافزار، جدول با نام Descriptive Statistics قرار دارد. به یاد داشته باشید، ما در تب Statistics از تنظیمات نرمافزار، گزینه Descriptives را انتخاب کردیم.
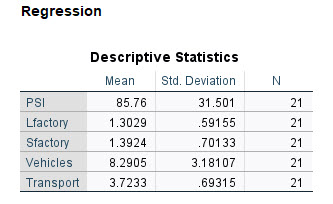
جدول Descriptive Statistics از نتایج این جدول میتوان میانگین، انحراف معیار و تعداد نمونه در هر Variable را به دست آورد. به عنوان مثال جدول بالا نشان میدهد، میانگین آلودگی هوا در 21 شهر مورد بررسی برابر با 85.76 واحد PSI بوده است. همچنین رتبه حمل و نقل عمومی به صورت میانگین، 3.72 واحد به دست آمده است.
جدول دیگر نتایج با نام Correlation نامیده میشود. در این جدول ضرایب همبستگی بین هر کدام از Variable ها با یکدیگر آمده است.
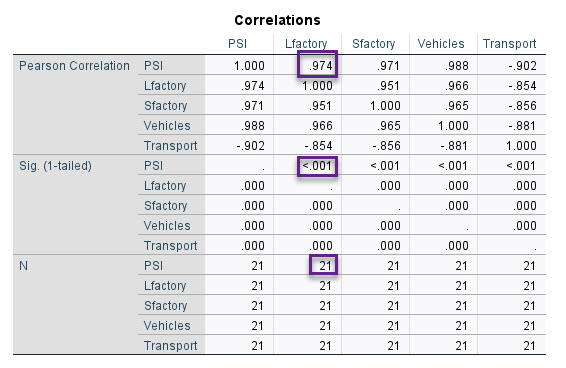
ماتریس Correlations در این جدول همانگونه که مشاهده میکنید، ضریب همبستگی بین هر کدام از X ها با Y و همچنین ضرایب همبستگی بین X ها به دست آمده است.
به عنوان مثال نتایج جدول بالا نشان میدهد ضریب همبستگی بین PSI و تعداد کارخانههای بزرگ Lfactory برابر با 0.974 واحد است. این نتیجه معنادار به دست آمده است (P-value < 0.001) و نشاندهنده وجود ارتباط مثبت و قوی بین آنها میباشد. واضح است که این بررسی بر روی 21 شهر انجام شده است.
جدول بعدی در خروجیهای نرمافزار با نام Variables Entered/Removed دیده میشود.
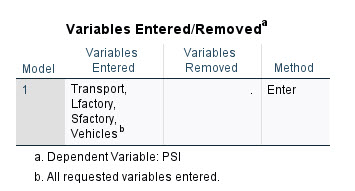
جدول Variables Entered/Removed از آنجا که من روش Enter را در ورود کمیتهای مستقل به مدل رگرسیونی انتخاب کردم، بنابراین همه Variableها همزمان وارد مدل شدهاند و هیچکدام نیز در فرایند اجرای مدل، حذف نشده است. علاقمند بودید در این زمینه لینک (انتخاب روشهای ورود کمیتهای مستقل به مدل رگرسیونی) را ببینید.
جدول بعدی با نام Model Summary از نتایج مفید و پرفایده در هر تحلیل رگرسیونی است. ابتدا آن را ببینید.

جدول Model Summary یکی از مهمترین آمارههایی که با استفاده از آن به سنجش مناسب بودن مدل رگرسیونی به دست آمده میپردازیم، ضریب تعیین یا R Square است. این اماره عددی بین صفر تا یک است و نشان میدهد مدل رگرسیونی به دست آمده تا چه اندازه میتواند درست کار کند و Xها چند درصد میتوانند Y یعنی کمیت پاسخ را توضیح داده و بیان کنند.
به عنوان مثال عدد ضریب تعیین در این مثال برابر با 0.988 شده است (R Square = 0.988). این عدد به وضوح بالا است و نشان میدهد، رگرسیون خطی برازش شده بر دادهها میتواند حدود 98.8 درصد خوب و مناسب باشد.
لازم به ذکر است، ما از ضریب تعیین مدل رگرسیون خطی جهت به دست آوردن اندازه اثر Effect Size نیز استفاده میکنیم. علاقمند بودید لینک (اندازه اثر Effect Size در مدلهای رگرسیون خطی) را مشاهده کنید. یک محاسبه ساده نشان میدهد اندازه اثر این مطالعه حدود 82.33 درصد است $ \displaystyle \left( {{{f}^{2}}=0.8233} \right)$.
بیایید جدول بعدی با نام ANOVA که به آن آنالیز واریانس نیز گفته میشود، را مشاهده کنیم. در ادامه دربارهی آن بیشتر توضیح میدهم.
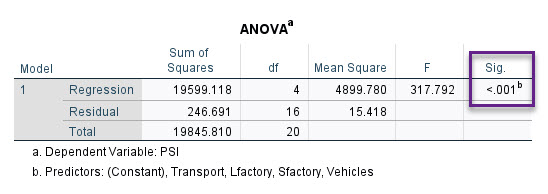
جدول آنالیز واریانس ئر تحلیل رگرسیونی حتماً تا به حال متوجه این نکته شدهاید که هر جا مقدار احتمال P-value محاسبه شده است، فرضیههای آماری وجود داشتهاند که مورد آزمون قرار گرفتهاند، به نظر شما در اینجا چه فرضیهای مورد آزمون قرار گرفته که مقدار احتمال آن در جدول ANOVA گزارش شده است؟ من در ادامه آنها را نوشتهام.
نتیجه به دست آمده در جدول ANOVA بالا، بیانگر رد فرض صفر و پذیرش فرض مقابل است (P-value < 0.001). این مطلب به معنای آن است که حداقل یکی از عوامل کارخانههای بزرگ و کوچک، تعداد وسایل نقلیه یا وضعیت حمل و نقل عمومی، بر آلودگی هوا موثر است. ما در جدول بعدی، یافتههای بیشتری در این زمینه خواهیم داشت.
میتوان بیان کرد که مهمترین یافته در تحلیل رگرسیون خطی، نتایج جدول Coefficients است. تصویر آن را در ادامه میبینید.
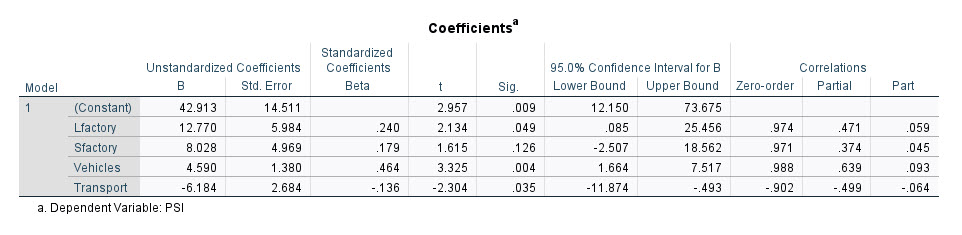
جدول Coefficients در تحلیل رگرسیون خطی در ادامه و به تفکیک بخشها و ستونهای مختلف این جدول را بیان میکنم.
ضرایب رگرسیونی مربوط به هر X در این ستون، براورد شده است. بر مبنای این ستون میتوانید معادله خط بین PSI با سایر Variableهای مستقل را بنویسیم.
$ \displaystyle y=42.91+12.77{{x}_{1}}+8.03{{x}_{2}}+4.59{{x}_{3}}-6.18{{x}_{4}}$
بر مبنای این معادله خط، به دست میآوریم که تعداد کارخانههای کوچک، بزرگ و وسایل نقلیه، بر آلودگی هوا تاثیر مستقیم و مثبت دارند. با این حال بهبود سیستم حمل و نقل عمومی، تاثیر کاهشی بر بیشتر شدن آلودگی هوا در شهرهای مورد بررسی داشته است.
از Std. Error نیز به نام انحراف معیار خطای ضرایب رگرسیونی نام برده میشود. کاربرد این آماره در محاسبه آماره آزمون ضرایب رگرسیونی یعنی t قرار دارد.
یکی از ایراداتی که به ضریب رگرسیونی غیراستاندارد، وارد است این است که واحد محور است و بر مبنای کوچکی یا بزرگی عدد ضریب B نمیتوانیم تاثیر X ها را با یکدیگر مقایسه کنیم. مثلا در این مقاله نمیتوانیم (صرفاً بر مبنای مشاهده عدد ضریب B) بگوییم تاثیر کارخانجات بزرگ بر آلودگی هوا بیشتر است یا تعداد وسایل نقلیه.
به منظور رفع این نقیصه، بهتر است از ضرایب رگرسیونی استاندارد شده Beta استفاده کنیم. این ضرایب از مدل رگرسیونی به دست میآیند که در آن هم Y و هم X ها استاندارد شدهاند. به منظور بررسی بیشتر این مسئله علاقمند بودید به کتاب روشهای پیشرفته آماری و کاربردهای آن – فصل هشتم مراجعه کنید.
در ستون Standardized Coefficients (Beta) عدد ضریب همبستگی استاندارد شده برای هر کدام از Variableها به دست آمده است. نتیجه به دست آمده در این ستون نشان میدهد، بیشترین تاثیر بر آلودگی هوا متعلق به کمیت تعداد وسایل نقلیه و در مرحلهی بعد تعداد کارخانههای بزرگ است.
به یک نکته مهم هم توجه کنید که از نظر تئوری و همواره، علامت مثبت یا منفی ضریب رگرسیونی استاندارد نشده با استاندارد شده، همانند و یکسان است.
آمارهی آزمون در جدول Coefficients دارای توزیع T Student است که مقدار آن در جدول ضرایب قابل مشاهده است. مقدار آماره t برای هر کدام از ضرایب رگرسیونی، از رابطهی زیر به دست میآید.
$ \displaystyle {{t}_{i}}=\frac{{{{b}_{i}}}}{{Se\left( {{{b}_{i}}} \right)}}$
که در آن $ \displaystyle {{{b}_{i}}}$ ضریب رگرسیونی براورد شده برای کمیت i ام است و $ \displaystyle {Se\left( {{{b}_{i}}} \right)}$ به عنوان انحراف معیار خطا همان کمیت در نظر گرفته میشود. نرمافزارهای آماری بر مبنای عدد به دست آمده برای آماره t به محاسبه مقدار احتمال P-value میپردازند.
نرمافزار SPSS، مقادیر احتمال در هر آزمون را با عنوان Sig نمایش میدهد. با استفاده از نتایج به دست آمده در این ستون میتوانیم بگوییم در یک سطح معنیداری خاص (مثلاً پنج درصد) کدام Variableها دارای اثر معنادار بر کمیت وابسته هستند.
به عنوان مثال نتایج ستون Sig جدول ضرایب در این مثال به ما میگوید که تعداد کارخانههای بزرگ (P-value = 0.049) و تعداد وسایل نقلیه (P-value = 0.004) دارای تاثیر افزایشی معنادار بر آلودگی هوا هستند. وضعیت حمل و نقل عمومی در شهرهای مورد بررسی نیز تاثیر معنادار کاهشی بر آلودگی هوا دارد (P-value = 0.035).
به خاطر داشته باشید من در تب Statistics از تنظیمات نرمافزار، گزینه Confidence intervals را فعال کردم. در اینجا میتوانم نتایج این گزینه را مشاهده کنم. در این ستونها کران بالا و پایین 95 درصد برای هر کدام از ضرایب رگرسیونی به دست آمده است.
به این نکته توجه کنید که فاصله اطمینان هنگامی که عدد صفر را در بر دارد به معنای این است که آن Variable فاقد تاثیر معنادار بر Y است و اگر عدد صفر را در بر نداشته باشد به معنای تاثیرگزاری معنادار بر کمیت پاسخ است.
در بخش Correlations سه ستون دیده میشود. من در تصویر زیر آنها را آوردهام.
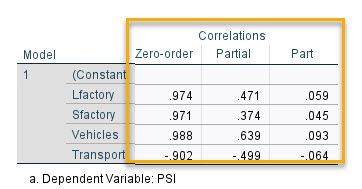
ستونهای Correlation در جدول ضرایب رگرسیونی ستون با نام Zero-order به بیان همبستگی ساده بین هر Variable با کمیت پاسخ میپردازد. نتایج این ستون را میتوانیم در جدول Correlations که ابتدای نتایج دربارهی آنها صحبت کردیم، مشاهده کنید.
ستون با نام Partial به بیان همبستگی جزئی Partial Correlation بین هر Variable با کمیت پاسخ میپردازد. من در لینک (همبستگی جزئی در نرمافزار SPSS) به توضیح و نحوه به دست آوردن این نوع از همبستگیها پرداختهام. علاقمند بودید آن را بخوانید.
در انتها نیز ستون Part وجود دارد. به این نوع همبستگی، همبستگی بخشی Part Correlation و یا نیمه جزئی Semi-Partial Correlation نیز گفته میشود. علاقمند بودید در این زمینه به لینک (همبستگی نیمه جزئی چیست؟) مراجعه کنید.
آخرین جدول در خروجیهای نرمافزار SPSS با نام Residuals Statistics دیده میشود. تصویر زیر را ببینید.
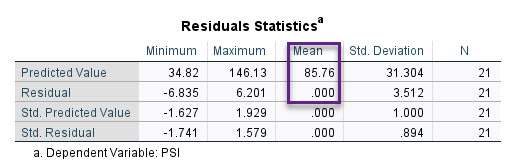
جدول Residuals Statistics در نتایج به دست آمده از این جدول میتوانیم آمارههای توصیفی مربوط به باقیماندههای مدل رگرسیونی و مقادیر پیشبینی شده Y را مشاهده کنیم. خوب است در این جدول به نکات مهم توجه کنیم.
چنانچه دقت کنید عدد به دست آمده برای میانگین مقادیر پیشبینی شده Y برابر با 85.76 است. این عدد دقیقاً برابر با میانگین مقادیر Y در جدول Descriptive Statistics است. به عبارت ساده رابطه $ \displaystyle \bar{y}=\bar{\hat{y}}$ همواره برقرار است.
در یک مدل رگرسیون خطی، میانگین باقیماندهها همواره برابر با صفر است. یعنی $ \displaystyle \bar{e}=0$.
پس از پایان یافتن جداول، گرافها و نمودارها در خروجی نرمافزار SPSS قرار دارد. این گرافها به دلیل انتخاب گزینههای دلخواه در تب Plots، به دست آمدهاند. در ادامه دربارهی آنها صحبت میکنیم.
نمودارها در رگرسیون خطیPlots
در خروجیهای نتایج نرمافزار، اولین گراف با نام هیستوگرام (Histogram) به بیان نحوه پراکندگی فراوانی باقیماندههای استاندارد شده Standardized Residual میپردازد. تصویر زیر را ببینید.
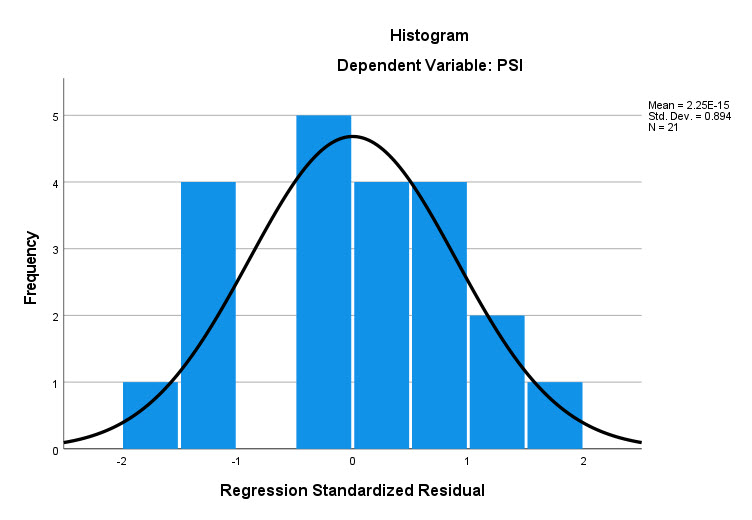
هیستوگرام باقیماندههای استاندارد شده یکی از پیشفرضهای انجام تحلیل رگرسیون خطی، نرمال بودن توزیع باقیماندهها است. با استفاده از این هیستوگرام میتوانیم منحنی نرمال باقیماندهها را مشاهده کنیم. چنانچه به یاد داشته باشید ما در تب Save تنظیمات نرمافزار، گزینه مشاهده باقیماندهها و مقادیر پیشبینی شده Y را انتخاب کردیم. در فایل دیتا، این نتایج به دست آمده است.
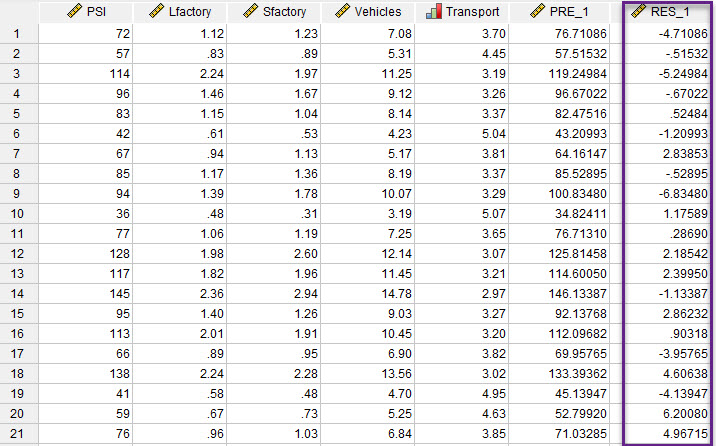
باقیماندهها و مقادیر پیشبینی شده برای کمیت وابسته هیستوگرام بالا، بر روی دادههای ستون RES در فایل دیتا رسم شده است. آزمون نرمال بودن این دادهها را نیز میتوانید با استفاده از نرمافزار SPSS انجام دهیم. علاقمند بودید این لینک را ببینید (آزمون نرمال بودن داده ها Normality Test در نرم افزار SPSS).
گراف دیگری که در خروجی نتایج دیده میشود نمودار احتمال نرمال (Normal Probability plot) است. آن را ببینید.
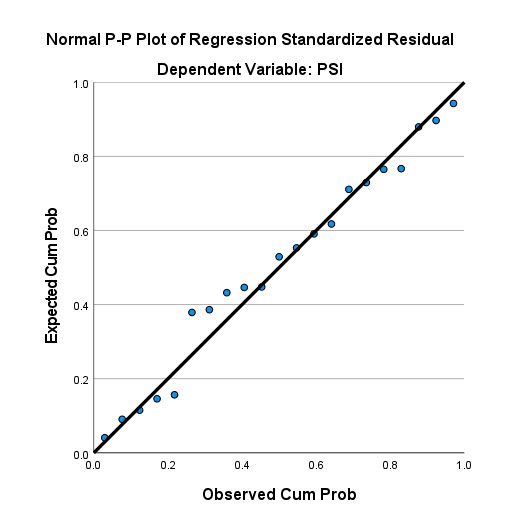
نمودار احتمال نرمال Normal Probability plot دربارهی این نمودار در بخش قبل توضیح دادیم. نمودار احتمال نرمال باقیماندهها در این مثال بیانگر توزیع مناسب باقیماندهها و نرمال بودن آنها است. (نقاط تقریباً در نزدیکی خط نیمساز قرار دارند.)
من در تب Plots از نرمافزار خواستم که گراف باقیماندههای استاندارد شده (ZRESID) در برابر کمیت وابسته (Dependent) را رسم کند. در تصویر زیر آن را ببینید.
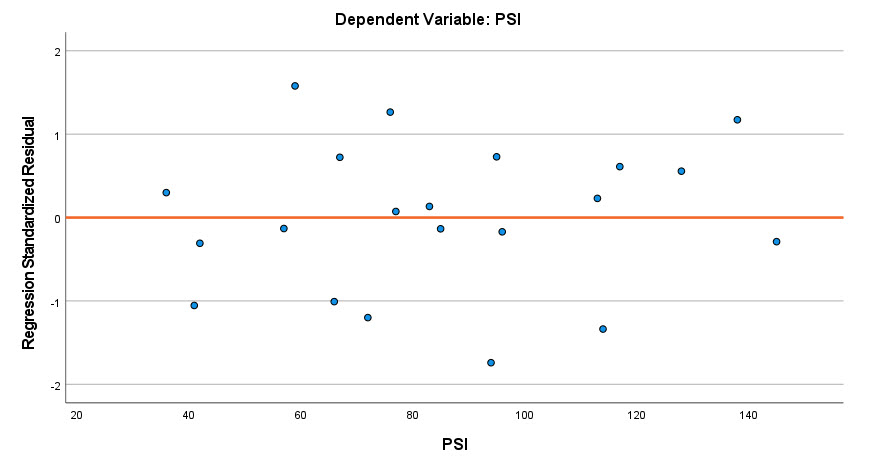
نمودار باقیماندههای استاندارد شده در برابر کمیت وابسته میدانیم که اگر مدل رگرسیونی برازش داده شده بر دادهها مناسب باشد، نمودار باقیماندههادر برابر کمیت پاسخ برازش شده بایستی نسبت به خط صفر متقارن بوده و نقاط حول این خط بطور یکنواخت پراکنده شده باشند.
نمودار بالا نحوهی پراکنش باقیماندههای استانداردشده را در برابر میزان آلودگی هوا نشان میدهد. نقاط به خوبی در اطراف خط صفر پراکنده شدهاند. این مطلب بیانگر برازش خوب معادله رگرسیونی به دست آمده، بر دادهها است.
به یاد داشته باشید در تنظیمات و در تب Plots گزینه Produce all partial plots را جهت به دست آوردن نمودارهای رگرسیون جزئی (Partial Regression plots)، انتخاب کردیم.
در ادامه این گرافها رسم شده است. نمودارها به تفکیک برای هر کدام ار X ها به دست آمده است. من در این لینک دربارهی این نمودارها بیشتر توضیح دادهام. (گرافهای رگرسیون جزئی در تحلیلهای رگرسیون خطی) علاقمند بودید آن را بخوانید.
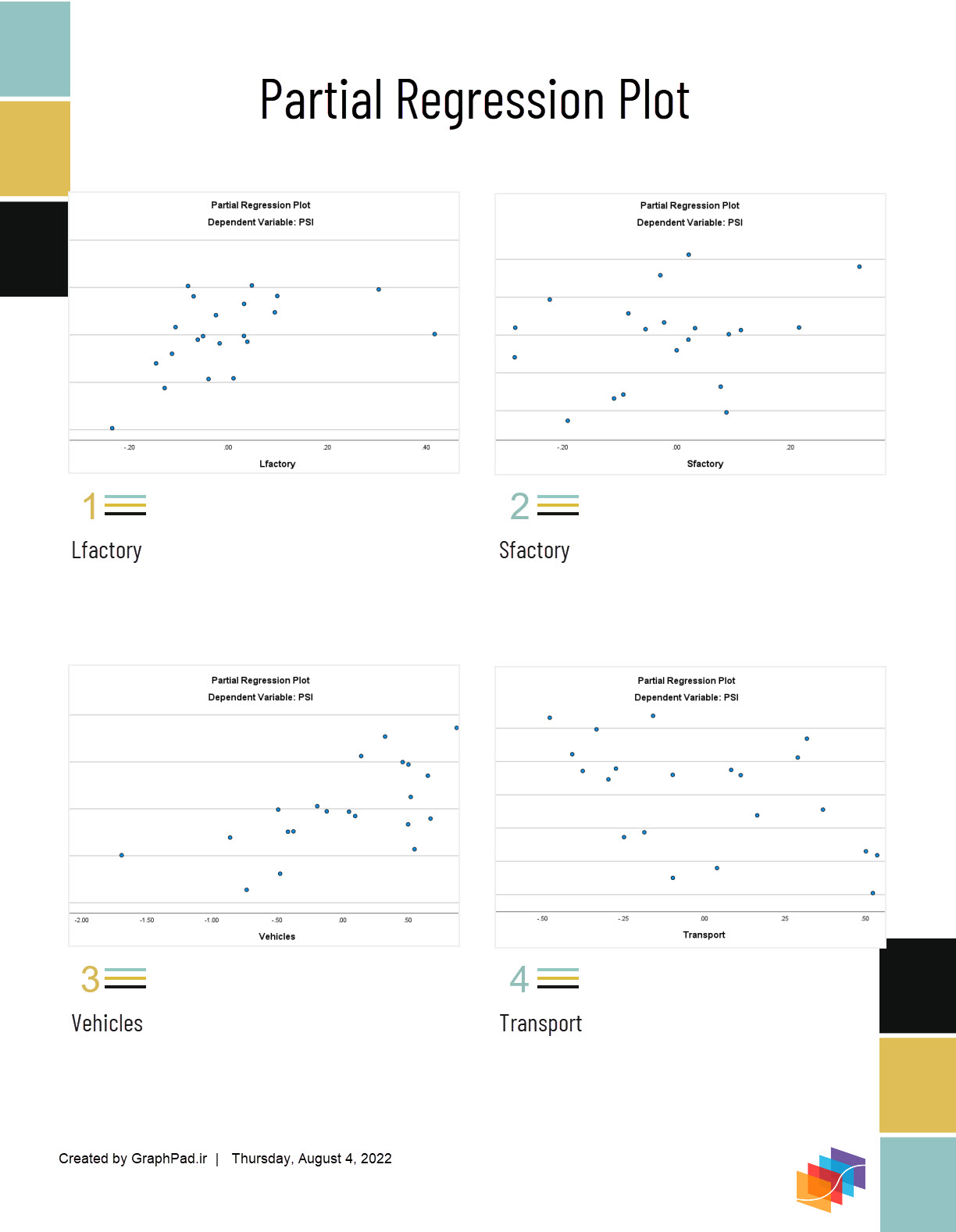
نمودارهای رگرسیون جزئی (Partial Regression plots) در این مقاله به موضوع طراحی مدل رگرسیون خطی Linear Regression با استفاده از نرمافزار SPSS پرداختیم. بیان مطالبی مانند آمارههای مورد استفاده، گرافها و نمودارها، براورد پارامترها و بررسی معیارهای مناسب بودن مدل به دست امده، در این مقاله مورد بررسی قرار گرفت. نحوه تنظیمات نرمآفزار SPSS و انتخاب گزینههای مهم و پرکاربرد، همراه با توضیح و تفسیر نتایج و خروجیةای به دست آمده، از دیگر موضوعات مورد بحث در این متن بود.چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2022). Linear Regression Models in SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/linear-regression-spss/.php
For example, if you viewed this guide on 12th January 2022, you would use the following reference
GraphPad Statistics (2022). Linear Regression Models in SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/linear-regression-spss/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.


