رگرسیون چندگانه Multiple Regression با گراف پد
یکی از بخشهایی که گراف پد در ورژن شماره 8 آن اضافه کرده است، توانایی انجام رگرسیون چندگانه و یا اصطلاحاً Multiple Regression است.
با استفاده از تحلیلهای رگرسیون چندگانه میتوانیم به صورت توام و همزمان اثرات چندین عامل و Variable را بر روی فاکتور پاسخ اندازهگیری کنیم.
ما در آموزش قبلی با نام طراحی مدل رگرسیون خطی Linear Regression با گراف پد پریسم که لینک آن را میتوانید از اینجا دریافت کنید، به انجام رگرسیون خطی ساده پرداختیم.
نکته اینکه رگرسیون خطی ساده به مدلی گفته میشود که تنها یک کمیت مستقل X در مدل وجود داشته باشد و بخواهیم ارتباط بین این X با کمیت پاسخ Y را به دست بیاوریم. مدلی که دارای چندین X باشد به مدل رگرسیون خطی چندگانه شناخته میشود. ما در این نوشتار قصد داریم درباره این مدل و آموزش نحوه انجام آن در نرم افزار گراف پد صحبت کنیم.
مدل آماری رگرسیون خطی چندگانه به صورت زیر نوشته میشود.
y = ß0 + ß1x1 + ß2x2 + … + ßkxk + ε
در این مدل میخواهیم بین x1 , x2 ,…, xk که کمیتهای رگرسیونی هستند با کمیت پاسخ y ارتباط برقرار کنیم. ε نیز به عنوان خطا و اشتباه در پیشبینی، استفاده میشود.
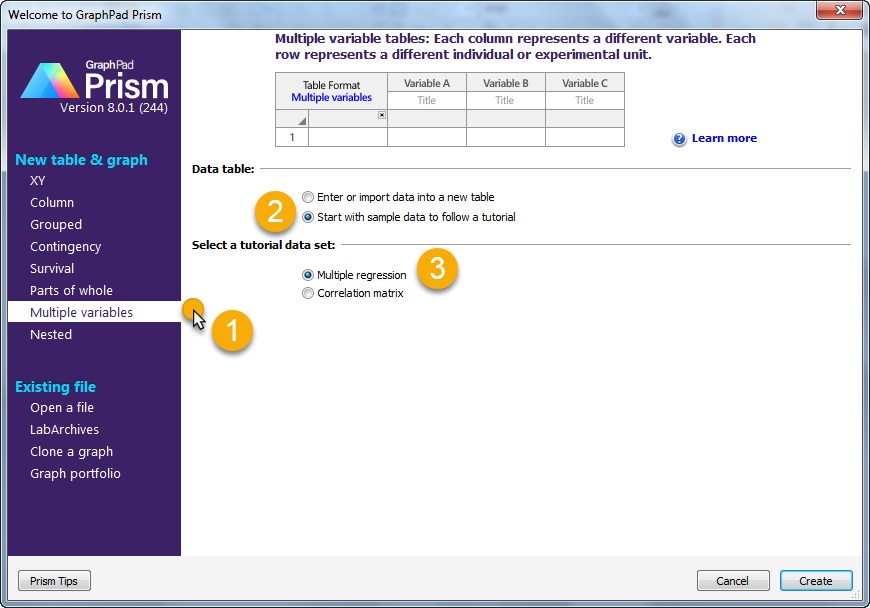
در نرم افزار پریسم 8 مکان انجام این نوع از آنالیز را در شکل زیر مشخص کردهام.
این مثال با نام Multiple regression در دسته تحلیلهای Multiple variables و در بخش Start with sample data to follow a tutorial قرار دارد. فایل مثال را میتوانید از اینجا دانلود کنید.
با Create کردن، دادهها و صفحه زیر برای ما باز خواهد شد. در مثال زیر تاثیر 9 عامل بر روی % Glycosylated hemoglobin بر اساس یک مدل رگرسیون چندبعدی سنجیده شده است.
در هر سطر نتایج مربوط به یک فرد خاص آمده است. در هر ستون نیز نتایج کمیت اندازهگیری شده برای آن فرد بیان شده است. هدف از این مطالعه آن است که بتوانیم با استفاده از مدل رگرسیون خطی چندبعدی، مقدار عددی glycosylated hemoglobin را از روی سایر کمیتها، پیشبینی کنیم.
در دادههای مثال ما، ده ستون دیده میشود. ستون اول با نام % Glycosylated hemoglobin همان Variable وابسته و Y مدل رگرسیونی است که قرار است مورد پیشبینی قرار بگیرد. ۹ ستون دیگر با اسامی
Hip in inches, Waist in inches, Weight in pounds, Height in inches, Male?, Age in years, HDL, Glucose, Total cholesterol
به عنوان Variableهای مستقل و Xهای مدل رگرسیونی، شناخته میشوند. ما میخواهیم با استفاده از این کمیتهای مستقل به برازش یک مدل رگرسیون خطی چندگانه و پیشبینی درصد Glycosylated hemoglobin با استفاده از آنها بپردازیم.
جهت انجام رگرسیون خطی چندگانه، در شیت دادهها، بر روی منوی Analyze کلیک کنید.
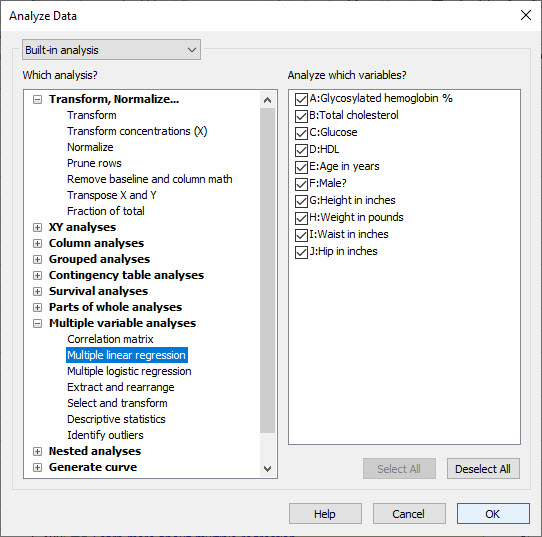
با انجام این کار، پنجره Analyze Data به صورت زیر برای ما باز شود.
در آنجا و از کادر Multiple variable analyses گزینه Multiple linear regression را انتخاب میکنیم. پنجره Parameters Multiple Linear Regression به صورت زیر برای ما باز میشود.
از تب Model و کادر Regression type گزینه Least squares, Assume Gaussian distribution of residuals را انتخاب میکنیم. بر مبنای این انتخاب یک مدل رگرسیون خطی که پارامترهای آن براساس روش کمترین مربعات، برازش میشود، به دست میآید. باقیماندههای این مدل، دارای توزیع نرمال فرض میشود.
البته میتوانستیم در همان شیت دادهها به صورت مستقیم وارد پنجره Parameters Multiple Linear Regression نیز شویم. برای اینکار در بالای منوی Analyze بر روی ابزارک Multiple Linear regression کلیک میکنیم.
در ادامه به توضیح بخشها و گزینههای مختلف پنجره Parameters Multiple Linear Regression که جهت انجام تحلیل رگرسیون خطی چندگانه، استفاده میشود، میپردازیم.
- Model
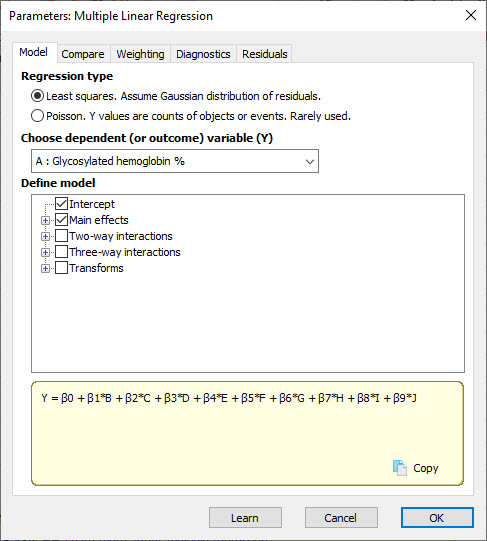
در این تب و در کادر choose dependent (or outcome) variable Y مشخص میکنیم که کمیت پاسخ، کدام است. به سادگی و بر مبنای شیت دادهها میدانیم که نام آن % Glycosylated hemoglobin میباشد. به صورت پیشفرض نیز همین ستون قرار گرفته است.
در کادر Define model میتوانیم نوع مدل رگرسیون خطی چندگانه خود را انتخاب کنیم. میدانیم که هر مدل رگرسیونی میتواند علاوه بر داشتن ضریب ثابت یا همان Intercept و اثرات اصلی Main effects ، شامل اثرات متقابل چند طرفه Interactions نیز باشد. چنانچه تمایل داشته باشیم میتوانیم این اثرات متقابل را نیز به مدل رگرسیونی خود اضافه کنیم.
بر مبنای مدل انتخاب شده در بخش Define model، در کادر زردرنگ پایین میتوانید معادله مدل رگرسیون را مشاهده کنیم.
- Compare
این تب از آن موارد به درد بخور و خاص نرمافزار گراف پد است. با استفاده از آن میتوانیم به مقایسه بین چند منحنی رگرسیونی بپردازیم و پارامترهای به دست آمده از هر مدل را با هم مقایسه کنیم.
از آنجا که در این مثال تنها یک منحنی رگرسیونی داریم، پس همان گزینه پیشفرض No comparison را میپذیریم. اگر به دنبال مقایسه بین دو منحنی رگرسیونی بودیم گزینه which of two models fits best را انتخاب میکنیم.
- Weighting
در این تب میتوانیم به وزندهی کمیت پاسخ Y بپردازیم. بر این اساس Y میتواند به معادلات دیگری تبدیل شود و سپس مدل رگرسیونی بر آن Y جدید تبدیل شده انجام گیرد. در این مثال قصد نداریم بر روی Y و یا همان % Glycosylated hemoglobin تبدیلی انجام دهیم، بنابراین گزینه No weighting را انتخاب میکنیم.
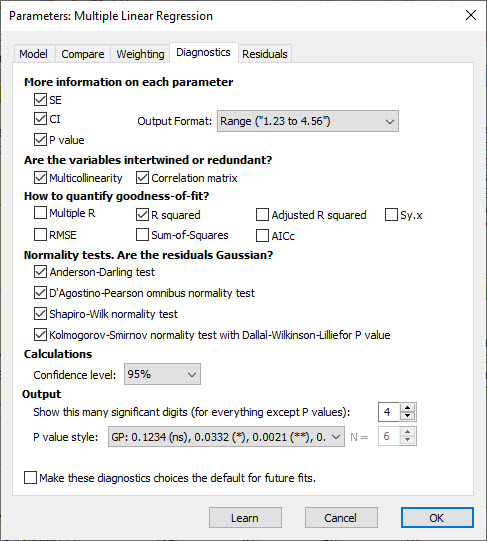
- Diagnostics
در این تب انواع آمارهها و معیارهای مناسبت مدل و نیکویی برازش وجود دارد. بخشهای مختلف آن را مشاهده میکنیم.
در ابتدا بخشی با نام More information on each parameter قرار دارد. در این بخش میتوانیم سه آمارهی SE خطای استاندارد، CI فواصل اطمینان و مقدار احتمال P value به ازای هر کدام از Xهای مدل را به دست آوریم. کادر Output Format نحوه نمایش اعداد را برای ما نشان میدهد.
در ادامه بخشی با نام Are the variables intertwined or redundant مشاهده میشود.
در این بخش دربارهی درهم تنیدگی Intertwined کمیتهای مستقل Xها در یکدیگر و احتمالاً زاید بودن Redundant آنها، صحبت میشود. با استفاده از بررسی همخطی چندگانه Multicollinearity و ماتریس همبستگی Correlation Matrix این موارد ارزیابی میشود.
یک توضیح کوتاه اینکه همخطی به معنای وجود ارتباط قوی و همبستگی بالا در بین Xهای مدل است. هر چند همخطی در همه مدلهای رگرسیونی وجود دارد اما شدت آن، یک نقیصه به حساب میآید. زیرا وقتی دو یا چند X با یکدیگر همخطی بالایی دارند، دیگر لزومی به آمدن همه آنها در مدل رگرسیونی نیست و زاید هستند.
به هرحال ما در این مثال هم در پی محاسبهی هم خطی و هم ماتریس همبستگی هستیم.
در بخش با نام How to quantify goodness-of-fit انواع آمارهها جهت سنجش میزان مناسب بودن مدل رگرسیون خطی چند بعدی آمده است. به صورت پیشفرض نرمافزار R square را انتخاب کرده است.
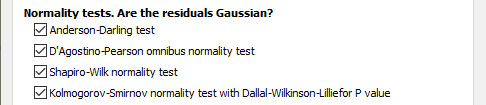
در بخش Normality tests. Are the residuals Gaussian به بررسی نرمال بودن باقیماندههای مدل رگرسیون خطی چند بعدی میپردازیم. این کار با استفاده از آزمونهای آماری با نامهای Kolmogorov-Smirnov, Shapiro-Wilk, D’Agostino-Pearson, Anderson-Darling انجام میشود. به دلخواه میتوانیم یک یا چند آزمون را حذف کنیم.
در بخش calculations به سادگی میتوانیم ضریب اطمینان فاصله اطمینان را مشخص کنیم. به صورت پیشفرض بر روی 95 درصد قرار دارد.
در بخش Output نیز میتوانیم تعداد رقمهای اعشار برای مقدار احتمال P value و قالب نمایش آن را انتخاب کنیم.
- Residuals
انواع گرافهای قابل رسم در تحلیل رگرسیون پواسن در تب Residuals دیده میشود. نرمافزار به صورت پیشفرض نمودار Residual plot که گرافی جهت بررسی باقیماندهها در برابر مقادیر Y پیشبینی شده است را رسم میکند. با استفاده از این گراف میتوانیم میزان درستی پیشبینی مدل رگرسیون خطی براورد شده را به دست بیاوریم. خوب است بقیه گرافها را نیز انتخاب کنیم. گرافهای رسم شده را در فولدر Graphs بعداَ میتوانیم مشاهده کنیم.
در پایان با OK کردن میتوانیم تمام نتایج و نمودارهای رسم شده در تحلیل رگرسیون خطی را مشاهده کنیم.
ابتدا به بررسی شیت نتایج که با نام Multiple lin. reg در فولدر Results پنجره راهبری سمت چپ نرمافزار قرار دارد، میپردازیم.
در این شیت میتوانیم بر مبنای تنظیماتی که در نرمافزار قرار دادیم، تمام تحلیلهای انجام شده رگرسیون خطی چندگانه را مشاهده کنیم. خطوط اولیه نوشته شده در نتایج بیان میکند که کمیت وابسته Dependent variable همان % Glycosylated hemoglobin است. نوع رگرسیون استفاده شده نیز Least squares است، دیده میشود.
ما در ادامه بخشهای مختلف صفحه نتایج را بیان میکنیم.
- Model
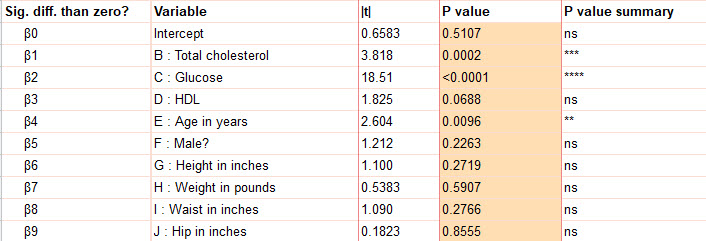
این بخش مهمترین نتایج تحلیل رگرسیون خطی چندگانه را شامل میشود. براورد پارامترهای β0 یعنی ضریب ثابت و β1 تا β9 که به کمیتهای اثرگزار بر % Glycosylated hemoglobin در مدل رگرسیونی مربوط میشوند، در این بخش آمده است.
این براوردها را میتوانیم در ستون با نام Estimate ببینیم. اگر عدد مثبت باشد به معنای تاثیرگزاری مستقیم و همجهت آن Variable با % Glycosylated hemoglobin است و اگر عدد براورد منفی باشد به معنای اثرگزاری وارون بین آن Variable با % Glycosylated hemoglobin است. به عنوان مثال براورد β4 که به معنای Age in years است، عددی مثبت و برابر با ۰.۰۱۳۶۵ به دست آمده است. بنابراین افزایش سن با افزایش % Glycosylated hemoglobin همراه خواهد بود. اندازه عددی ۰.۰۱۳۶۵ نیز بیانگر آن است که به شرط ثابت ماندن بقیه Variableها، افزایش یکسال سن، به اندازه ۰.۰۱۳۶۵ درصد سبب افزایش % Glycosylated hemoglobin میشود.
به عنوان مثال دیگر براورد β5 که به معنای ?Male است، عددی منفی و برابر با ۰.۲۷۶۸- به دست آمده است. بنابراین مرد بودن سبب کاهش % Glycosylated hemoglobin خواهد بود. اندازه عددی ۰.۲۷۶۸- نیز نشان میدهد به شرط ثابت ماندن سایر کمیتها، مرد بودن به اندازه ۰.۲۷۶۸ واحد % Glycosylated hemoglobin را کاهش میدهد.
به همین ترتیب درباره سایر Variableها میتوانیم اظهارنظر کنیم. درباره معنادار بودن و یا فاقد اثرگزاری معنادار در هر Variable بعداَ صحبت خواهیم کرد.
علاوه بر براورد پارامترها، خطای استاندارد و فواصل اطمینان 95 درصد به ازای هر پارامتر نیز در جدول بالا آمده است. خوبی فواصل اطمینان این است که با استفاده از آنها و حتی بدون داشتن مقادیر احتمال P value، میتوانیم تاثیر معناداری یا عدم معنادار آن پارامتر بر پاسخ (در اینجا % Glycosylated hemoglobin) را به دست آوریم.
در این زمینه توضیح اینکه اگر فواصل اطمینان شامل عدد صفر باشند، نتیجه میگیریم آن پارامتر تاثیر معنادار بر Y یا همان پاسخ ندارد. به عنوان مثال در اینجا فاصله اطمینان پارامتر درمان HDL عدد صفر را در بر دارد. بنابراین نتیجه میگیریم HDL بر % Glycosylated hemoglobin اثر معنادار ندارد. ?Male نیز همینگونه است.
اگر هر دو کران فاصله اطمینان از عدد صفر کمتر و منفی باشند، بیانگر وجود ارتباط معنادار آن هم از نوع وارون بین آن X با Y است. در این مثال فاصله اطمینان با هر دو کران منفی، دیده نمیشود.
اگر هر دو کران فاصله اطمینان از عدد صفر بیشتر و مثبت باشند، بیانگر وجود ارتباط معنادار از نوع مستقیم بین آن X با Y است. به عنوان مثال در اینجا Total cholesterol دارای فواصل اطمینان مثبت هستند و بنابراین بر % Glycosylated hemoglobin تاثیر مستقیم افزایشی و معنادار دارد.
به این ترتیب با استفاده از اعداد به دست آمده برای پارامترها میتوانیم % Glycosylated hemoglobin برای هر فرد را محاسبه کنیم. مدل رگرسیون خطی چندگانه در مثال ما به صورت زیر خواهد بود.
y = -1.381 + 0.0068 x1 + 0.0276 x2 – 0.0085 x3 + 0.0136 x4 – 0.2768 x5 + 0.0305 x6 – 0.0027 x7 + 0.0323 x8 – 0.0060 x9
با استفاده از این مدل میتوانیم با قرار دادن Xهای دلخواه به ازای هر فرد حتی خارج از این مطالعه، درصد Glycosylated hemoglobin او را محاسبه کنیم.
- Sig. diff. than zero
آمارهی t به همراه مقدار احتمال P value آزمون، به ازای هر کدام از Xهای مدل، در این بخش بیان شده است.
آنجه که به وضوح دیده میشود و در بخش بالا و بیان فواصل اطمینان نیز به آن اشاره شد، این است که Variableهای مستقل Total cholesterol با (P value = 0.0002) و Glucose با (P value < 0.0001) و Age in years با (P value = 0.0096) بر درصد Glycosylated hemoglobin دارای تاثیر معنادار هستند. در ستون P value summary این کمیتها با ستاره مشخص شدهاند. میدانیم که تعداد ستاره بیشتر به معنای معناداری قویتر است. سایر کمیتها بر درصد Glycosylated hemoglobin تاثیر معنادار ندارند.
- Goodness of Fit
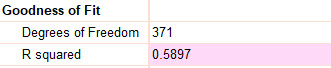
همانگونه که میدانیم R square که در فارسی به آن ضریب تعیین میگوییم عددی بین صفر تا یک است و نشاندهندهی آن است که مدل رگرسیونی به دست آمده تا چه اندازه میتواند پراکندگی دادههای واقعی را تحت پوشش خود قرار دهد. در واقع ضریب تعیین میتواند ابزاری جهت سنجش قدرت پیشبینیکنندگی و خوب بودن مدل باشد. هر چه عدد R square به مقادیر یک نزدیکتر باشد، بیانگر بهتر بودن مدل رگرسیون به دست آمده است.
همانگونه که در جدول بالا مشاهده میکنید اندازه عددی R square برابر با 0.5897 به دست آمده است. این عدد تقریباَ متوسط است و نشان میدهد مدل رگرسیون خطی به دست آمده میتواند ۵۸.۹۷ درصد پراکندگی دادهها را تحت پوشش خود قرار دهد.
- Analysis of Variance
پاسخ به این سوال که مدل رگرسیونی به دست آمده معنادار و قابل قبول است در بخش Analysis of Variance و یا همان آنالیز واریانس آمده است.
مقدار احتمال به دست آمده (P value < 0.0001) به سادگی بیانگر آن است که مدل رگرسیون خطی چندگانه که در این مثال به دست آوردیم، قابل قبول و معنادار است. به عبارت دیگر با استفاده از Variableهای ۹گانه بالا، میتوان با درصد خوبی کمیت پاسخ % Glycosylated hemoglobin را پیشبینی کرد.
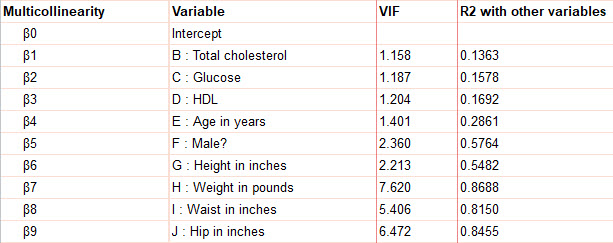
- Multicollinearity
ما در پنجره Parameters Multiple Linear Regression و در تب Diagnostics در بخش Are the variables intertwined or redundant به هنگام تنظیمات مدل، گزینههای Multicollinearity و Correlation Matrix را جهت به دست آوردن نتایج همخطی و ماتریس همبستگی، فعال کردیم. در جدول زیر میتوانید نتایج هم خطی بین Variableها را مشاهده کنید.
هم خطی با آمارهای به نام فاکتور تورم واریانس Variance Inflation Factor (VIF) سنجیده میشود. اندازه VIFها نشان میدهد با همبسته بودن کمیتها به یکدیگر، واریانس ضریب رگرسیونی براورد شده به چه میزان افزایش مییابد.
اگر VIF نزدیک به یک باشد، همخطی بین آن X با کمیتهای دیگر وجود ندارد، اما اگر VIFها از یک بزرگتر باشند، همخطی بین آن X با کمیتهای دیگر وجود دارد. وقتی VIF > 5 باشد، ضریب رگرسیونی به دست آمده برای آن جمله، مناسب نیست و معمولاً آن X را حذف میکنیم.
در جدول بالا کمیتهای Weight in pounds و Waist in inches به همراه Hip in inches دارای مقدار VIF بالایی هستند. به معنای اینکه همخطی شدیدی بین این Variableها با سایر Xها وجود دارد. بنابراین بهتر است به منظور به دست آوردن یک مدل رگرسیونی بهتر، آنها را حذف کنیم. بررسی P value این سه Variable نیز بیانگر عدم تاثیرگزاری معنادار آنها بر کمیت پاسخ است.
در جدول بالا ستون دیگری با نام R2 with other variables دیده میشود. اعداد به دست آمده برای هر کمیت نشان میدهد که اگر آن X نقش Y را در یک مدل رگرسیونی داشته باشد و سپس بین آن X که دیگر Y شده است و سایر X ها یک مدل رگرسیونی برقرار کنیم، در آن صورت، ضریب تعیین این مدل رگرسیونی چقدر خواهد بود.
به عنوان مثال عدد 0.1363 برای Total cholesterol بیان میکند که اگر یک مدل رگرسیونی بین Total cholesterol از یک طرف و هشت Variable دیگر، برقرار کنیم، ضریب تعیین یا همان R2 این مدل رگرسیونی جدید حدود 13.63 درصد خواهد بود.
همانگونه که میدانیم R2 عددی بین صفر و یک است و هرچقدر به یک نزدیکتر باشد، نشاندهندهی وجود ارتباط قویتر بین کمیت پاسخ Y با سایر کمیتهای مستقل Xها میباشد.
در مدلهای رگرسیونی مطلوب آن است که بین Xها همخطی وجود نداشته باشد و اندازههای VIF آن نزدیک به یک و R2 with other variables در اطراف صفر باشد.
- Correlation matrix
در ادامه مباحث هم خطی که در بالا به آن اشاره کردیم، نرمافزار گراف پد ماتریس همبستگی بین کمیتهای مستقل را نیز رسم کرده است. این ماتریس که آرایههای آن عدد ضریب همبستگی بین هر X با X دیگر میباشد، نشان میدهد ارتباط جفتی بین کمیتهای مستقل با یکدیگر چگونه است.
به عنوان مثال عدد 0.1288- نشان میدهد ارتباط بین Total cholesterol و Glucose منفی و حدود 13 درصد میباشد. برای بقیه Xها نیز عدد ضریب همبستگی به دست آمده است.
- Normality of Residuals
یادتان باشد در پنجره Parameters Multiple Linear Regression و در تب Diagnostics در بخش ?Normality tests. Are the residuals Gaussian به هنگام تنظیمات مدل، گزینههای مربوط به بررسی نرمال بودن باقیماندههای مدل رگرسیونی را فعال کردیم. در جدول زیر میتوانید نتایج این بررسی را مشاهده کنید.
بر مبنای هر چهار آزمون مورد بررسی، باقیماندههای مدل، فاقد توزیع نرمال هستند و آزمون نرمال بودن باقیماندهها، رد میشود.
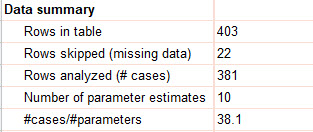
- Data summary
در این بخش خلاصهای از دادههای مثال رگرسیون خطی چند بعدی را مشاهده میکنید. جدول زیر بیان میکند که ۴۰۳ سطر (فرد) مورد بررسی قرار گرفته است. تعداد ۲۲ سطر که تحت عنوان داده گمشده Missing data و شامل افراد دارای عدم پاسخ است، در این مثال دیده میشود. این افراد از مطالعه کنار گذاشته شدهاند. بنابراین ۳۸۱ نفر در این مطالعه آنالیز شدهاند.
تعداد ۱۰ پارامتر یعنی همان پارامترهای β3 ، β2 ، β1 ، β0 تا β9 براورد شدهاند. نسبت تعداد افراد به پارامترها یعنی 381/10 برابر با 38.1 به دست آمده است.
آنچه در این مثال همچنان باقی مانده است، مشاهده و رسم گرافهای متناظر با تحلیل رگرسیون خطی میباشد. در فولدر Graphs پنجره سمت چپ میتوان عناوین پنج شیت از نمودارهای رسم شده در این مثال را مشاهده کرد.
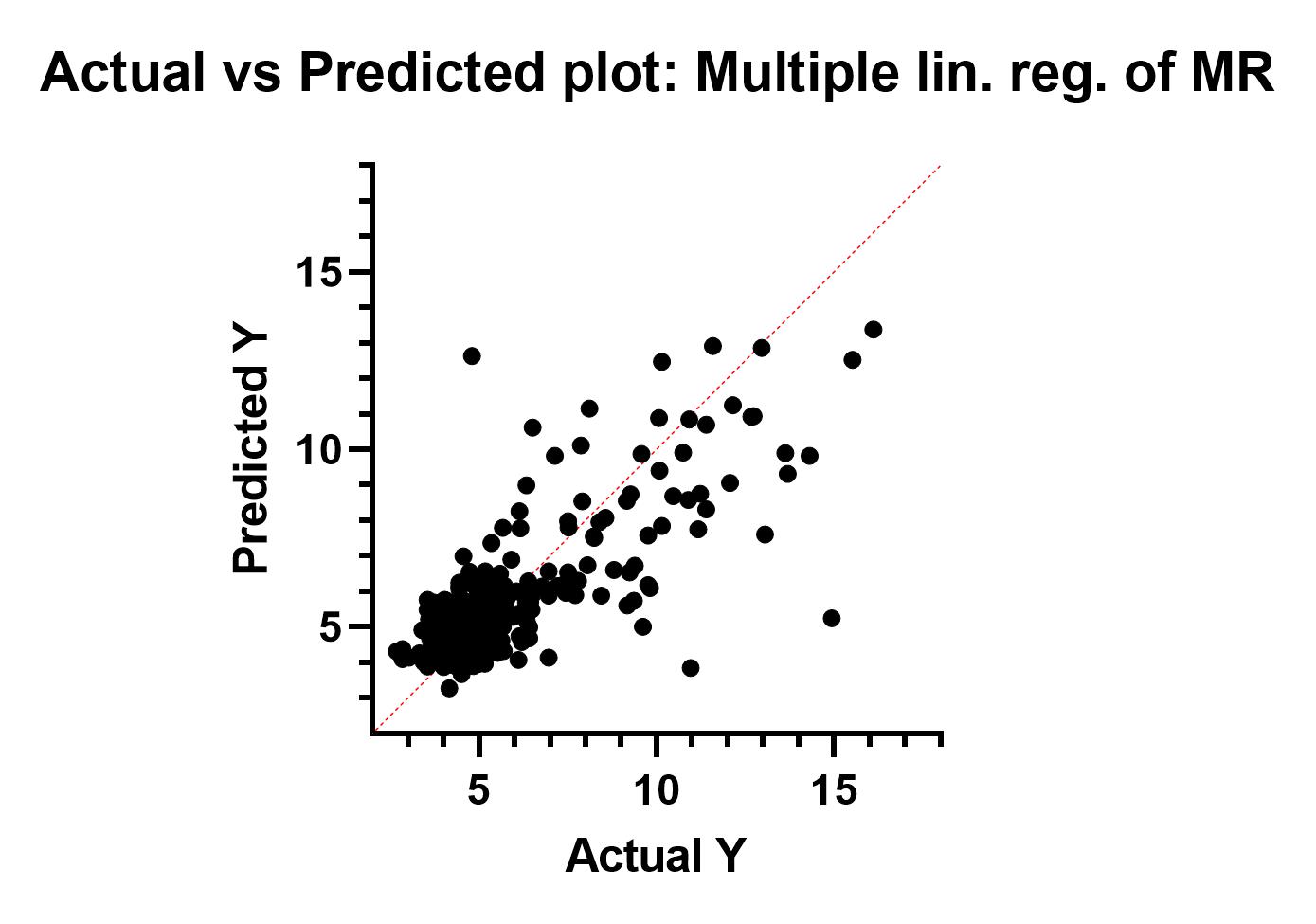
در ادامه به بررسی این گرافها میپردازیم. در ابتدا از گراف Actual vs Predicted plot: Multiple lin. reg شروع میکنیم. شکل آن را در زیر میتوانید ببینید.
در این گراف محور عمودی مقادیر Y پیشبینی شده با استفاده از مدل رگرسیون خطی است. به این معنا که بر مبنای Xهای هر فرد به دست آوردهایم درصد Glycosylated hemoglobin او چقدر میتواند باشد. هر دایره نیز بیانگر یک فرد میباشد.
در محور افقی نیز عدد واقعی % Glycosylated hemoglobin آمده است. دقت کنید که خط نیمساز نقاطی را نشان میدهد که اندازههای واقعی و پیشبینی شده با یکدیگر برابرند. این بهترین حالت برای مدل است که بیانگر خطای صفر پیشبینی میباشد. با این حال همانگونه که مشاهده میکنید، برخی از نقاط از خط نیمساز دور هستند، به معنای اینکه مدل به دست آمده چندان مناسب نیست. در مواردی نیز که نقاط بر روی خط نیمساز و یا اطراف آن هستند، به معنای آن است که مدل رگرسیونی به دست آمده مناسب است و خطای مدل اندک است.
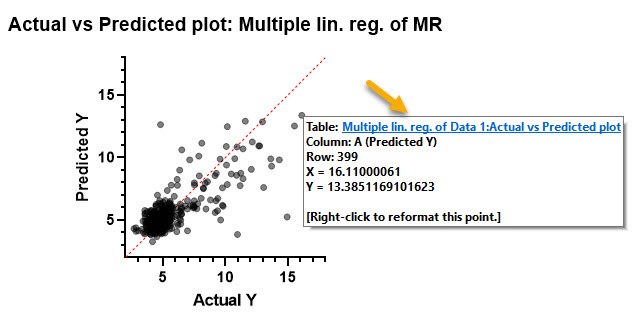
چنانچه علاقمند باشیم اعداد پیشبینی شده Y برای درصد Glycosylated hemoglobin را به ازای هر فرد مشاهده کنیم، میتوانیم در گراف بالا، بر روی یک دایره دلخواه برویم. اطلاعاتی درباره همان نقطه در صفحه گراف برای ما مشخص خواهد شد. به عنوان مثال میتوانیم ببینیم آن نقطه سطر چندم دادهها است، اندازه X آن (در اینجا مقدار واقعی درصد Glycosylated hemoglobin) چقدر است و اندازه Y یعنی پیشبینی درصد Glycosylated hemoglobin برای آن نقطه چقدر خواهد بود.
به عنوان مثال در نقطه انتخابی ما که مربوط به سطر ۳۹۹ است، محور X که همان عدد واقعی درصد Glycosylated hemoglobin است برابر با ۱۶.۱۱ بوده است. برای همین نقطه محور Y که عدد پیشبینی شده برای درصد Glycosylated hemoglobin است برابر با ۱۳.۳۸ شده است. در این نقطه تا حدی خطای پیشبینی دیده میشود.
به همین ترتیب خط آبیرنگ با نام Multiple lin. reg. of Data: Actual vs Predicted plot در کادر بالا دیده میشود. اگر بر روی آن کلیک کنیم به صورت مستقیم به نتایج و شیت Results میرویم. در آنجا یک تب جدید با نام Actual vs Predicted plot ساخته شده است. در زیر میتوانید ببینید.
در این شیت از نتایج، چند ستون دیده میشود. در ستون X با نام Actual Y عدد واقعی درصد Glycosylated hemoglobin به ازای هر فرد دیده میشود. در ستون دیگر با نام Predicted Y به ازای همان فرد، تعداد دفعات پیشبینی شده درصد Glycosylated hemoglobin توسط مدل رگرسیون خطی چند بعدی، مشاهده میشود. فاصله و اختلاف بین این ستونها همان خطا و باقیمانده مدل رگرسیونی نامیده میشود.
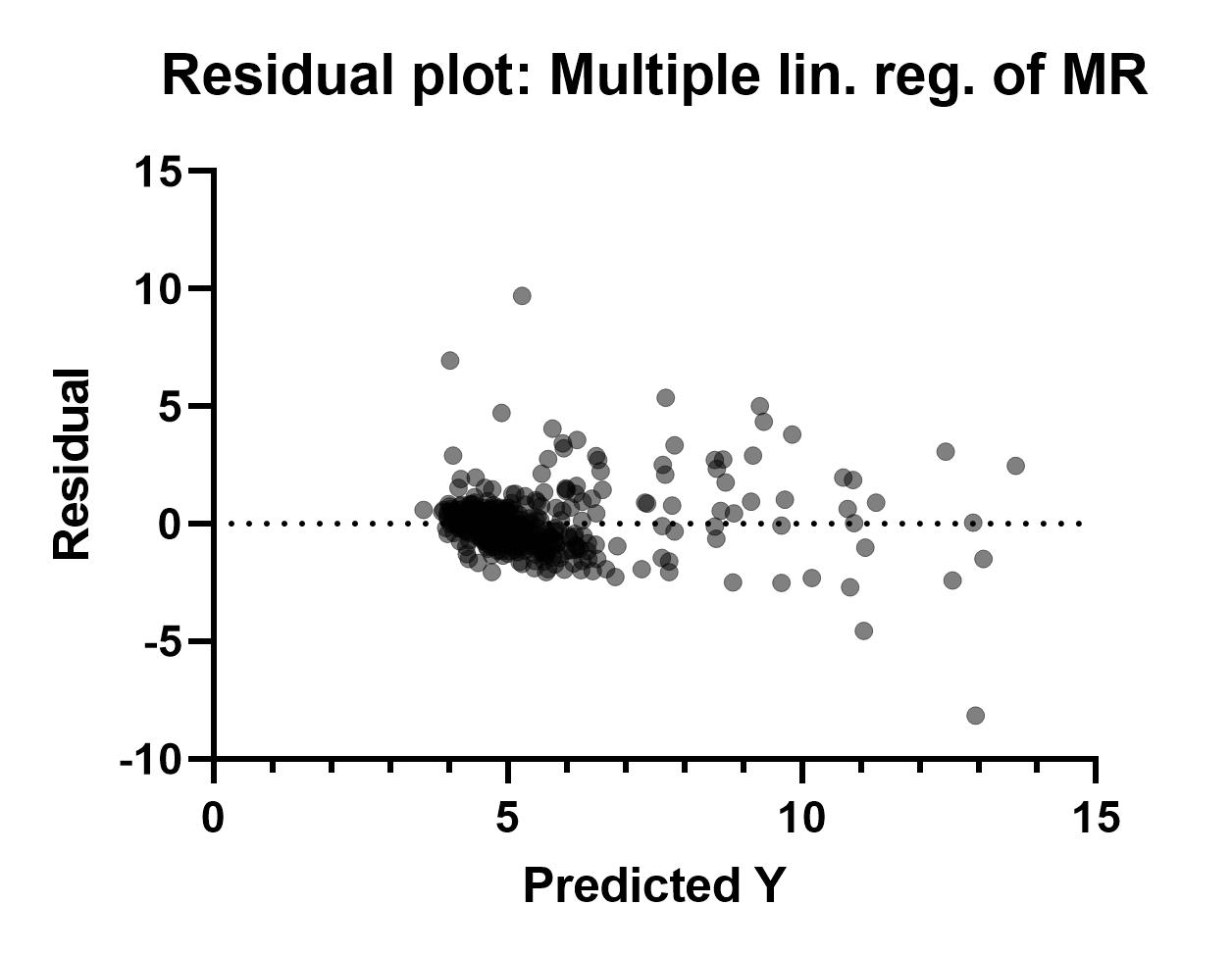
حال به بررسی گراف دیگر با نام Residual plot: Multiple lin. reg. of Data بپردازیم.
در این نمودار میتوانیم باقیماندهها و یا همان خطاهای مدل رگرسیونی به ازای هر فرد را مشاهده کنیم. توضیح اینکه باقیمانده به اختلاف بین مقدار واقعی درصد Glycosylated hemoglobin و مقدار پیشبینی شده برای آن گفته میشود. مدل رگرسیونی خوب است که در گراف بالا نقاط به صورت تصادفی در اطراف خط صفر قرار گرفته باشند. در این مثال تقریباَ چنین چیزی به خوبی دیده میشود.
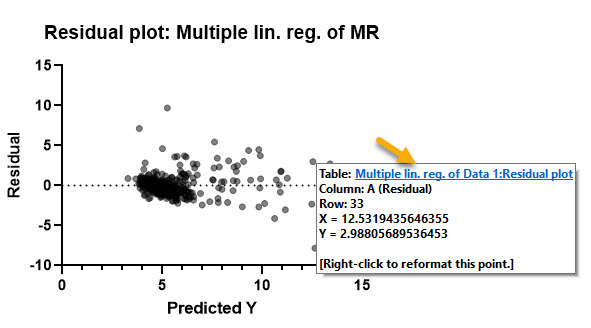
همانند گراف بالا با قرار دادن موس بر روی هر دایره، میتوانیم مختصات X یعنی عدد پیشبینی شده برای درصد Glycosylated hemoglobin و Y یعنی اندازه خطای مدل را مشاهده کنیم.
به عنوان مثال در نقطه انتخابی ما که مربوط به سطر ۳۳ است، محور X که همان عدد پیشبینی شده درصد Glycosylated hemoglobin است برابر با ۱۲.۵۳ شده است. برای همین نقطه محور Y که مقدار خطای مدل رگرسیونی را نشان میدهد برابر با ۲.۹۹ شده است.
با کلیک کردن بر روی عبارت آبی رنگ Multiple lin. reg. of Data: residual plot میتوانیم در شیت نتایج تب دیگری با نام Residual plot به دست میآید. در تصویر زیر میتوانید آن را ببینید.
همانگونه که مشاهده میشود به ازای هر فرد میتوان مقدار عدد پیشبینی شده برای درصد Glycosylated hemoglobin و خطای پیشبینی را مشاهده کرد.
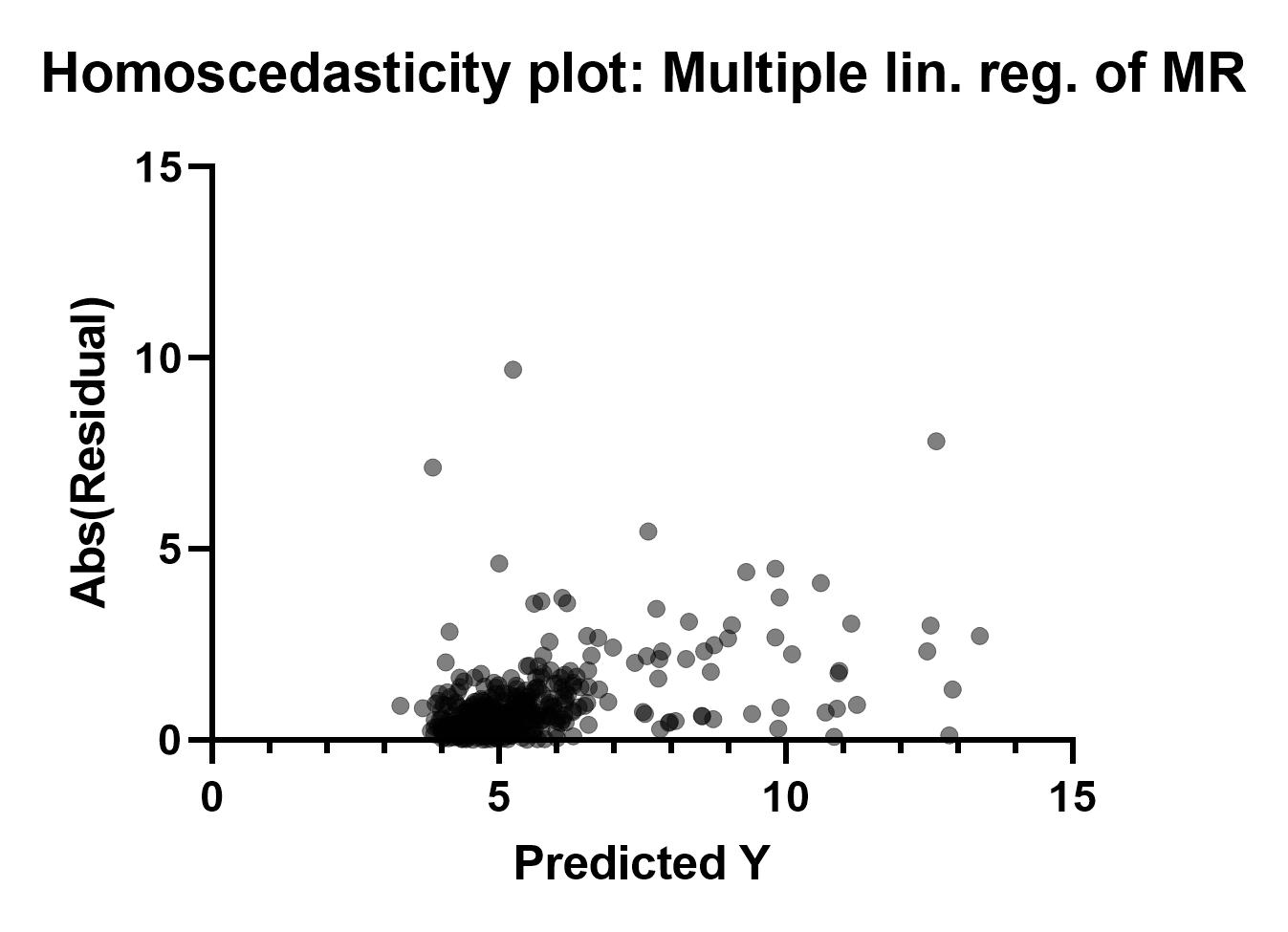
گراف دیگر با نام Homoscedasticity plot: Multiple lin. reg. of MR همان گراف بالا است با این تفاوت که قدر مطلق باقیماندهها در محور عمودی قرار گرفته است. این نکته لازم به ذکر است که باقیماندهها از آنجا که به صورت اختلاف بین مقدار مشاهده شده و عدد پیشبینی شده هستند، میتوانند به صورت مثبت و یا منفی باشند. یعنی در مواردی عدد واقعی بزگتر باشد و باقیمانده مثبت شود و در مواردی عدد پیشبینی شده بزرگتر باشد و باقیمانده منفی شود.
در شکل زیر میتوانید گراف را مشاهده کنید.
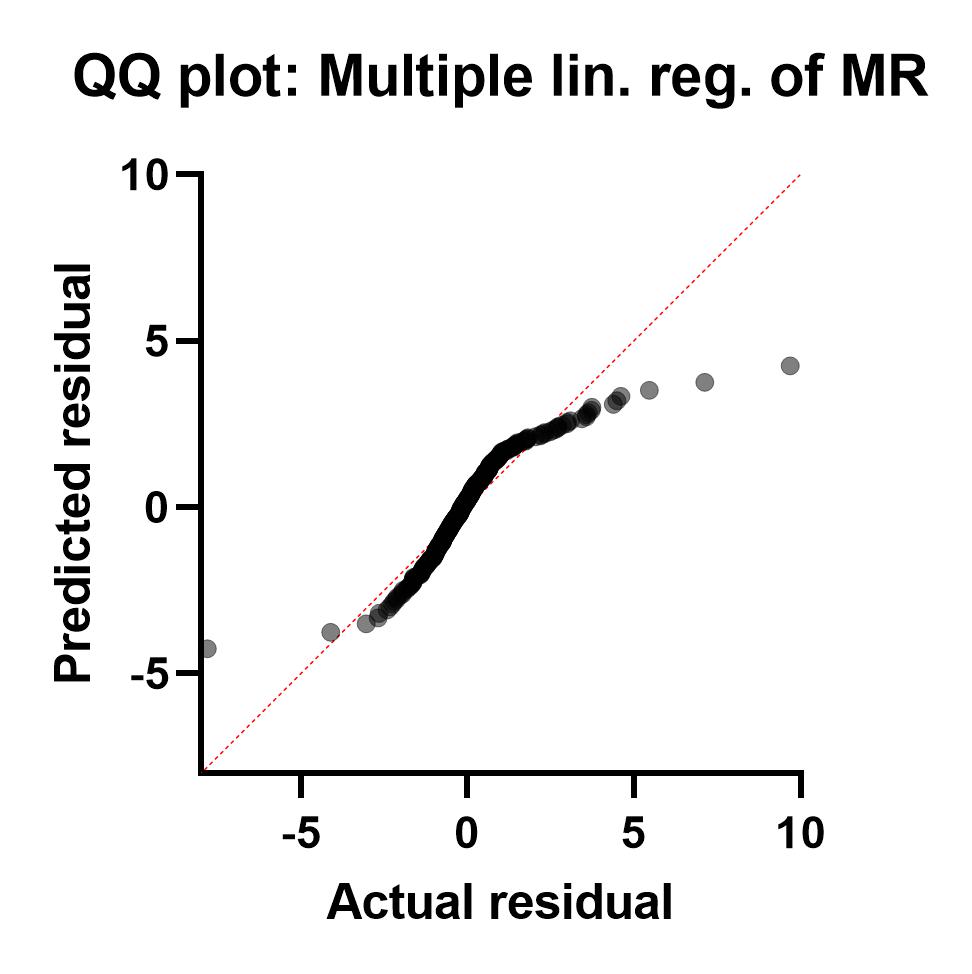
گراف دیگر با نام QQ plot: Multiple lin. reg. of MR دیده میشود. این گراف به بررسی نرمال بودن توزیع باقیماندههای مدل میپردازد. محور افقی گراف بیانگر باقیماندههای واقعی و محور عمودی نشاندهندهی باقیماندههای پیشبینی شده براساس مدل رگرسیونی است. چنانچه دادهها بر روی خط نیمساز قرار بگیرند، نتیجه میگیریم که توزیع باقیماندهها نرمال است.
در شکل زیر میتوانید QQ Plot این مثال را مشاهده کنید. به نظر میرسد انحراف از خط نیمساز زیاد است و توزیع باقیماندههای مدل، نرمال نیست. یادتان باشد در نتایج به دست آمده نیز به این نکته رسیدیم که بر مبنای هر چهار روش Kolmogorov-Smirnov, Shapiro-Wilk, D’Agostino-Pearson, Anderson-Darling توزیع باقیماندهها نرمال نبود. گراف به دست آمده در شکل زیر تاییدی بر این نتیجه است.
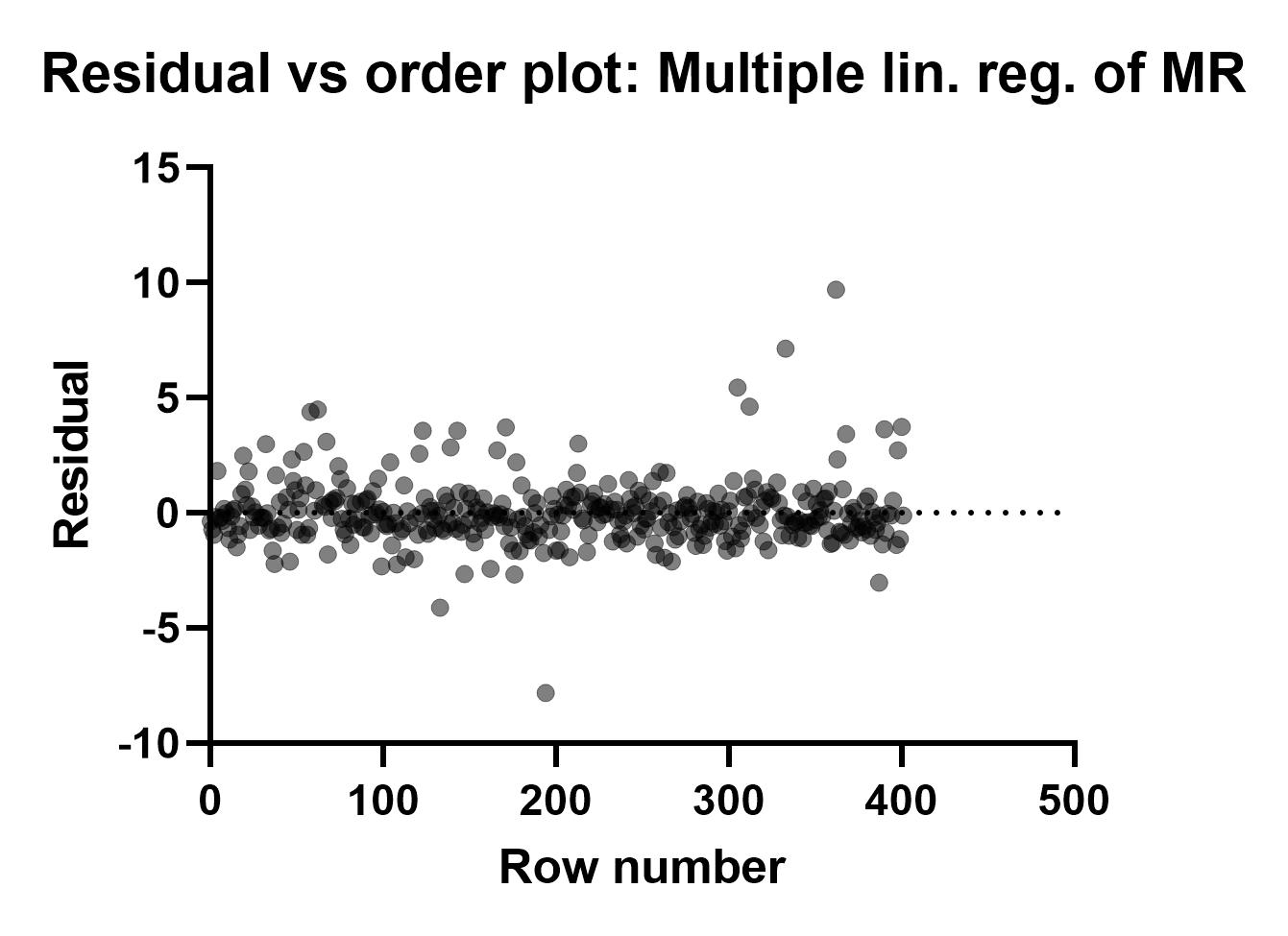
آخرین گراف با نام Residual vs order plot: Multiple lin. reg. of MR به دست آمده است. ابتدا شکل آن را ببینید.
در این تصویر باقیماندهها (محور Y) در برابر ترتیب و ردیف افراد (محور X) قرار گرفتهاند. به معنای اینکه از نفر ابتدا تا نفر انتها (نفر ۴۰۳ام) به ترتیب باقیمانده و خطای مدل رگرسیون خطی به ازای هر کدام از آنها آمده است. همانند گرافهای بالا میتوانیم با قرار دادن موس بر یک نقطه، تب نتایج را مشاهده کنیم.
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2020). Multiple Regression with GraphPad Prism Software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/multiple-regression/.php
For example, if you viewed this guide on 12th January 2022, you would use the following reference
GraphPad Statistics (2020). Multiple Regression with GraphPad Prism Software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/multiple-regression/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.