همبستگی جزئی Partial Correlation در نرم افزار SPSS

همبستگی به مفهوم ارتباط میان دو یا چند کمیت با یکدیگر است و ضریب همبستگی مقدار عددی این ارتباط را بیان می‌کند. وقتی از ضریب همبستگی در جامعه صحبت می‌کنیم با مفهوم پارامتری آن روبه‌رو هستیم که آن را با نماد ρ نشان می‌دهیم و وقتی از جامعه نمونه‌گیری می‌شود، براورد نمونه‌ای آن را با r نمایش می‌دهیم.

دریافت ویدئو آموزش ضرایب همبستگی با نرم‌افزار SPSS

شامل 100 دقیقه ویدئو، 34 اسلاید، فایل‌های دیتا و نتایج نرم‌افزار SPSS

اندازه عددی ضریب همبستگی نزدیک به مقادیر منفی یک به معنای وجود یک ارتباط قوی و وارون است که اندازه‌های عددی دو کمیت در جهت عکس یکدیگر رفتار می‌کنند. اندازه‌های عددی نزدیک به صفر نیز بدان معنا است که تغییرات یک کمیت، اطلاع کمی درباره تغییرات کمیت دیگر در اختیار ما قرار می‌دهد. نکته‌ای که باید در این میان به آن توجه کرد این است که ضریب همبستگی صفر و یا نزدیک صفر را نباید به مفهوم استقلال کمیت‌ها از یکدیگر دانست. هر چند که ضریب همبستگی دو کمیت مستقل از یکدیگر، همواره صفر است.

ضریب همبستگی جزئی

 Partial Correlation Coefficient 

همبستگی جزئی Partial Correlation ابزاری جهت بررسی رابطه خطی Linear Relationship بین دو کمیت پیوسته است که در عین حال تاثیر یک یا چند کمیت پیوسته دیگر (معمولاً از آن‌ها تحت عنوان کمیت‌های کمکی Covariate یا کنترلی Control نام برده می‌شود) را کنترل می‌کند.

نکته بسیاری از تحلیل‌های همبستگی جزئی را می‌توان با استفاده از رگرسیون چندگانه Multiple Regression مورد بررسی قرار داد. گاهی توصیه می‌شود به جای استفاده از ضریب همبستگی جزئی از رگرسیون‌های چندگانه استفاده کنید. به هر حال شما می‌توانید مطالعات مربوط به اندازه اثر و رابطه بین کمیت‌ها را هنگامی که با کنترل کننده‌ها روبه‌رو هستید، هم به صورت همبستگی‌های جزئی و هم تحلیل‌های رگرسیونی انجام دهید.

پیش فرض‌های انجام تحلیل همبستگی جزئی

 Assumptions 

هنگامی که تصمیم می‌گیرید داده‌های خود را با استفاده از همبستگی جزئی آنالیز کنید، بخشی از فرآیند تحلیل، شامل بررسی پیش فرض‌هایی است تا مطمئن شوید داده‌هایی که می‌خواهید تحلیل کنید واقعاً می‌توانند با استفاده از این روش آنالیز شوند. ما در یک تحلیل Partial Correlation با پنج پیش‌فرض روبه‌رو هستیم.

قبل از اینکه شما را با این پنج فرض آشنا کنیم، تعجب نکنید اگر هنگام تحلیل داده‌های خود، یک یا چند مورد از این فرضیات نقض شد (یعنی برآورده نشد).

زمانی که با داده‌های دنیای واقعی کار می‌کنید، به جای نمونه‌های کتاب درسی، (که اغلب به شما نشان می‌دهد چگونه یک همبستگی جزئی را زمانی که همه چیز خوب پیش می‌رود، انجام دهید) به شما نشان می‌دهد، حتی زمانی که داده‌های شما برخی از مفروضات را براورده نمی‌کنند، اغلب راه حلی برای غلبه بر آن وجود دارد. ابتدا، بیایید به این پنج فرض نگاهی بیندازیم.

 پیش‌فرض 2  در یک تحلیل همبستگی جزئی لازم است یک یا چند Covariate و یا همان Control Variables داشته باشیم. در غیر این صورت مطالعه ما از نوع همبستگی ساده که با نام Bivariate شناخته می‌شود، خواهد بود.

 پیش‌فرض 3  باید یک رابطه خطی بین کمیت‌ها وجود داشته باشد. یعنی همه جفت کمیت‌های ممکن، باید یک رابطه خطی را نشان دهند. این کار را می‌توان با استفاده از یک Scatter Plot انجام داد.

 پیش‌فرض 4  هیچ نقطه پرت قابل توجهی Significant Outliers نباید وجود داشته باشد. نقاط پرت صرفاً نقاط داده منفردی در داده‌های شما هستند که از الگوی معمول پیروی نمی‌کنند. همبستگی جزئی به موارد پرت حساس است، که می‌تواند تاثیر بسیار زیادی بر روی خط بهترین تناسب و ضریب همبستگی داشته باشد و منجر به نتیجه‌گیری نادرست در مورد داده‌ها شود. بنابراین، بهترین کار این است که هیچ داده پرتی وجود نداشته باشد یا به حداقل برسد. بررسی وجود داده‌های پرت را می‌توانیم با استفاده از رسم یک Box Plot در نرم‌افزار SPSS انجام دهیم.

 پیش‌فرض 5  کمیت‌های شما باید حداقل به طور تقریبی توزیع نرمال داشته باشند Approximately Normally Distributed. برای انجام این کار، باید نرمال بودن دو بعدی Bivariate Normality را برای هر جفت کمیت داشته باشید، اما ارزیابی این فرض دشوار است، بنابراین روش ساده‌تری معمولاً استفاده می‌شود که به موجب آن وجود توزیع نرمال برای هر کمیت به صورت جداگانه آزمایش می‌شود. این را می‌توان با استفاده از آزمون نرمال بودن Shapiro-Wilk یا kolmogorov-Smirnov انجام داد.

در این جا خوب است به این نکته اشاره کنم که وجود واژه Approximately می‌تواند به ما این یافته را برساند که عدم نرمال بودن داده‌ها، همچنان نتایج تحلیل همبستگی جزئی را معتبر، نگه خواهد داشت. بنابراین چنانچه در بررسی نرمالیتی، توزیع نرمال داشتن داده‌ةای شما تایید نشد، همچنان می‌توانید از Partial Correlation استفاده کنید.

مثال همبستگی جزئی

 Example 

به عنوان مثال می‌خواهیم رابطه بین برخی از شاخص‌های قلبی و عروقی مانند chol، crp و sbp را به دست بیاوریم. با این حال کمیت‌هایی مانند وزن و یا سن افراد باید در این مطالعه کنترل شوند. بنابراین خوب است جهت سنجش رابطه بین شاخص‌ها، از وزن و سن به عنوان کنترل کننده‌ها در یک تحلیل همبستگی جزئی استفاده کنیم.

 بیایید این بحث را با استفاده از نرم‌افزار SPSS توضیح دهیم. فایل دیتای این مثال را می‌توانید از اینجا و با نام Partial Correlation Coefficient دریافت کنید.

در ابتدا به بررسی پیش فرض‌های پنج گانه بالا می‌پردازیم. واضح است که شاخص‌ها، سن و وزن دارای مقیاس Scale و پیوسته هستند. همچنین ما در این مطالعه کمیت‌های سن و وزن را به عنوان کنترل کننده داریم. بنابراین تا اینجا پیش فرض‌های 1 و 2 جهت انجام تحلیل همبستگی جزئی، تایید می‌شود.

پیش فرض شماره 3 به وجود رابطه خطی بین کمیت‌ها، اشاره می‌کند. همان‌گونه که بیان کردیم این کار را می‌توانیم با استفاده از رسم گراف‌هایی با نام Scatter Plot انجام دهیم. من در این لینک (رسم نمودار پراکنش Scatter Plot با استفاده از نرم‌افزار SPSS) به آموزش نمودارهای پراکنش پرداخته‌ام، می‌توانید آن را ببینید.

پیش‌فرض شماره 4 به بررسی وجود داده‌های پرت در مطالعه می‌پردازد. این کار را می‌توانیم با استفاده از رسم گراف‌های Box Plot انجام دهیم. به همین ترتیب من در لینک رسم نمودار جعبه ای Box Plot با استفاده از نرم‌افزار SPSS به آموزش این گراف‌ها و یافتن داده‌های پرت با استفاده از آن‌ها پرداخته‌ام. آن را مشاهده کنید.

پیش فرض شماره 5 نرمال بودن توزیع داده‌ها را بیان می‌کند. در لینک آزمون نرمال بودن داده ها Normality Test در نرم افزار SPSS، می‌توانید به بررسی وجود توزیع نرمال در داده‌ها بپردازید.

حال بیایید به موضوع اصلی این مقاله یعنی تحلیل همبستگی جزئی بپردازیم. جهت انجام این تحلیل از مسیر زیر در نرم‌افزار SPSS استفاده می‌کنیم.

Analyze → Correlate → Partial 

پنجره زیر با نام Partial Correlation برای ما باز می‌شود.

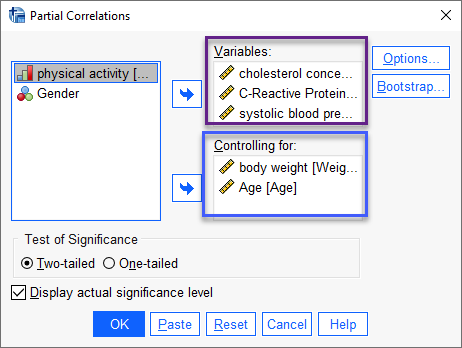
در کادر Variables همان کمیت‌هایی را که می‌خواهیم ضریب همبستگی بین آن‌ها به دست بیاید، قرار می‌دهیم. در واقع ما در این مطالعه می‌خواهیم همبستگی و رابطه بین شاخص‌های chol، crp و sbp را به دست بیاوریم.

از آن‌جا که وزن و سن به عنوان کمیت‌های کنترلی و کووریت، مطرح هستند، بنابراین آن‌ها را در بخش controlling for قرار می‌دهیم.

چنانچه علاقمند باشیم، نتایج بیشتری به دست بیاوریم، بر روی تب Options بزنید، با این کار وارد پنجره زیر می‌شویم.

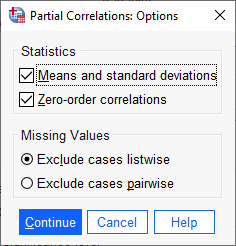
در این پنجره گزینه‌های Means and standard deviations و Zero-order correlations را انتخاب می‌کنیم. این کار سبب می‌شود آماره‌های توصیفی از کمیت‌ها و همچنین ماتریس همبستگی ضرایب بدون در نظر گرفتن کنترل کننده‌ها، در خروجی نتایج به دست بیاید.

نتایج و خروجی‌های نرم‌افزار

 Output 

Continue کرده و سپس OK می‌کنیم. به این ترتیب نتایج و خروجی‌های زیر در Output نرم‌افزار SPSS به دست می‌آید.

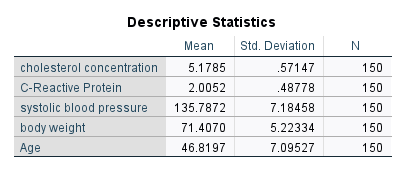
در ابتدا و در جدول بالا، آماره‌های توصیفی مانند میانگین، انحراف معیار و تعداد نمونه به ازای هر کدام از کمیت‌های مطالعه، بیان شده است. به سادگی می‌توانید آن‌ها را در جدول بالا ببینید.

در ادامه نتایج، جدول با نام Correlation در خروجی نرم‌افزار دیده می‌شود.

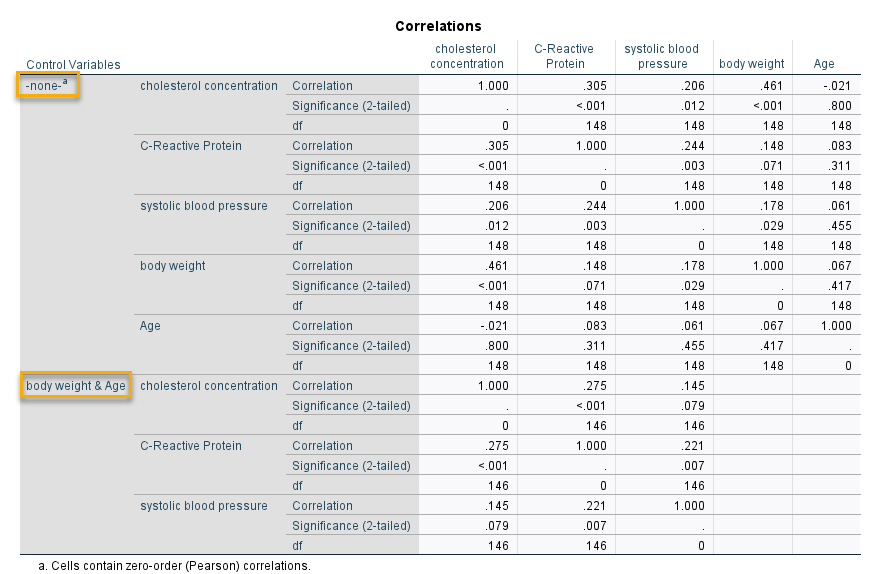
جدول Correlation در دو بخش بیان شده است. یک بخش با نام none که در آن ضریب همبستگی از نوع پیرسن، بین هر کدام از کمیت‌ها به دست آمده است.

به عنوان مثال ضریب همبستگی بین chol و crp عدد 0.305 شده است. در این جدول می‌توانید عدد ضریب همبستگی پیرسن به همراه مقدار احتمال معناداری Sig را مشاهده کنید. نتایج این بخش مربوط به حالتی است که ما هیچ کمیت کنترل کننده و کووریت نداریم و همگی Variable ها، مستقل در نظر گرفته شده‌اند.

بخش دیگر جدول Correlation مربوط به حالتی است که سن و وزن تحت عنوان کنترل کننده، وارد تحلیل‌های همبستگی شده است. نتایج این بخش همان موضوع همبستگی جزئی و بررسی رابطه بین کمیت‌ها، با حضور مداخله‌گرها است.

به عنوان مثال همان رابطه بین chol و crp با ورود کنترل کننده‌های با نام سن و وزن، تعدیل می‌شود و عدد ضریب همبستگی جزئی بین آن‌ها برابر با 0.275 و البته همچنان معنادار، به دست می‌آید.

معنادار بودن رابطه بین chol و crp بدون در نظر گرفتن کنترل‌ها و با در نظر گرفتن کنترل کننده‌ها، نشان می‌دهد که سن و وزن تاثیر کمی بر کنترل رابطه chol و crp دارند.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2022). Partial Correlation Coefficient in SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/partial-correlation-spss/.php

For example, if you viewed this guide on 12^th January 2022, you would use the following reference

GraphPad Statistics (2022). Partial Correlation Coefficient in SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/partial-correlation-spss/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.