انواع مدل‌های خطی تعمیم یافته GLM و GEE در نرم افزار SPSS

 Types of Generalized Linear Models  

مجموعه آموزش نرم‌افزار SPSS

کامل‌ترین مجموعه فارسی زبان آموزش نرم‌افزار SPSS

 

من در این مقاله می‌خواهم به بیان و توضیح هر کدام از این مدل‌ها و شرایط کار با آن‌ها بپردازم. در واقع این مقاله به دلیل اهمیت انتخاب درست نوع مدل در تحلیل‌های تعمیم یافته GLM و GEE نوشته شده است. در این مقاله در پی این هستیم که به شرح و توضیح زمان کاربرد معادلات و مدل‌های موجود در منوی آنالیزهای تعمیم یافته در نرم‌افزار SPSS بپردازیم.

ابتدا خوب است بدانیم که در نرم‌افزار SPSS می‌توانیم تحلیل‌های تعمیم یافته GLM و GEE را با استفاده از مسیر زیر پیدا کرده و انجام دهیم. ما در ادامه و مقالات دیگر به نحوه کار با این مدل‌ها و دلایل کاربرد آن‌ها خواهیم پرداخت.

پنجره انواع مدل‌ها

 Type of Models 

هنگامی که در SPSS به مسیر مدل‌های خطی تعمیم یافته Generalized Linear Models (GLM) و معادلات براوردکننده تعمیم یافته Generalized Estimating Equations (GEE) می‌رویم، پنجره زیر باز می‌شود.

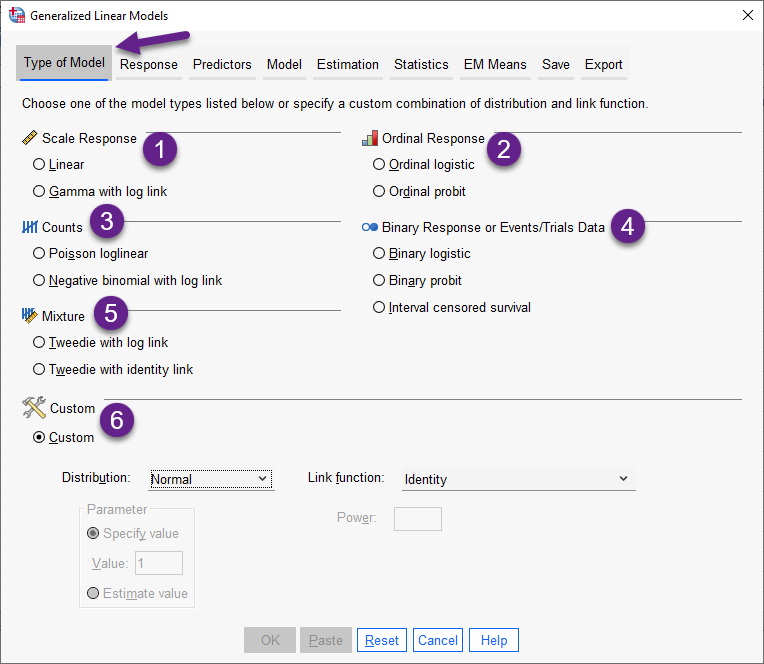
در این پنجره می‌توانیم انواع مدل‌های تعمیم یافته موجود در نرم‌افزار SPSS را ببینیم. همان‌گونه که گفتم ما در این مقاله می‌خواهیم صرفاً درباره‌ی این پنجره و مدل‌های موجود در آن صحبت کنیم. من پنجره Type of Model و بخش‌های مختلف آن را شماره‌گزاری کرده‌ام، در ادامه به ترتیب درباره‌ی هر کدام از این بخش‌ها صحبت می‌کنم.

نکته موضوع مهمی که قبل از شروع بحث و بیان مدل‌های تعمیم یافته وجود دارد، این است که نحوه انتخاب و یا دلیل کار کردن با هر کدام از این مدل‌ها به ماهیت و توزیع داده‌های کمیت پاسخ و وابسته یا همان Dependent Variable بستگی دارد. به معنای اینکه ابزار در اختیار ما جهت اینکه از کدام مدل استفاده کنیم، همان نوع داده‌های کمیت پاسخ Response است. در واقع ما کاری به کمیت‌های مستقل Independent Variable ها نداریم و آنچه که باعث می‌شود یکی از مدل‌ها و معادلات تعمیم یافته را برای کار خود مناسب ببینیم و دیگری را مناسب نداریم، کمیت پاسخ مطالعه ما خواهد بود.

نکته دیگر با اهمیت در اینجا انتخاب تابع پیوند Link function است. این تابع به ما نشان می‌دهد که ارتباط بین کمیت پاسخ با کمیت‌های مستقل چگونه و از طریق چه تابع ریاضی انجام شود. در واقع تابع پیوند تبدیلی است که بر روی داده‌های پاسخ اعمال می‌شود. پس از آن تحلیل بر روی داده‌های تبدیل شده انجام می‌شود. در این زمینه در ادامه بیشتر صحبت می‌کنیم.

خب، حال بیایید به توضیح هر کدام از بخش‌های پنجره Type of Model بپردازیم.

 1. Scale Response  هنگامی که کمیت پاسخ مطالعه از نوع عددی Scale باشد از مدل‌های موجود در این بخش استفاده می‌کنیم. این مدل‌ها به صورت زیر هستند.

این مدل هنگامی استفاده می‌شود که توزیع داده‌های پاسخ (کمیت وابسته مطالعه) از نوع نرمال باشد. همچنین این انتخاب سبب می‌شود تابع پیوند بین DV و IVها، به صورت Identity تعریف شود. این تابع پیوند به صورت $ \displaystyle f\left( x \right)=x$ تعریف می‌شود. به معنای ساده یعنی اینکه تبدیلی بر روی داده‌های پاسخ انجام نمی‌شود و تحلیل بر روی خود داده‌ها رخ می‌دهد. خوب است این نکته را بدانید که تابع پیوند از نوع Identity می‌تواند بر روی هر تابع توزیعی استفاده شود.

شاید این سوال را بپرسید که تابع پیوندها را از کجا می‌توان انتخاب کرد. پاسخ به این سوال در تصویر زیر قرار دارد.

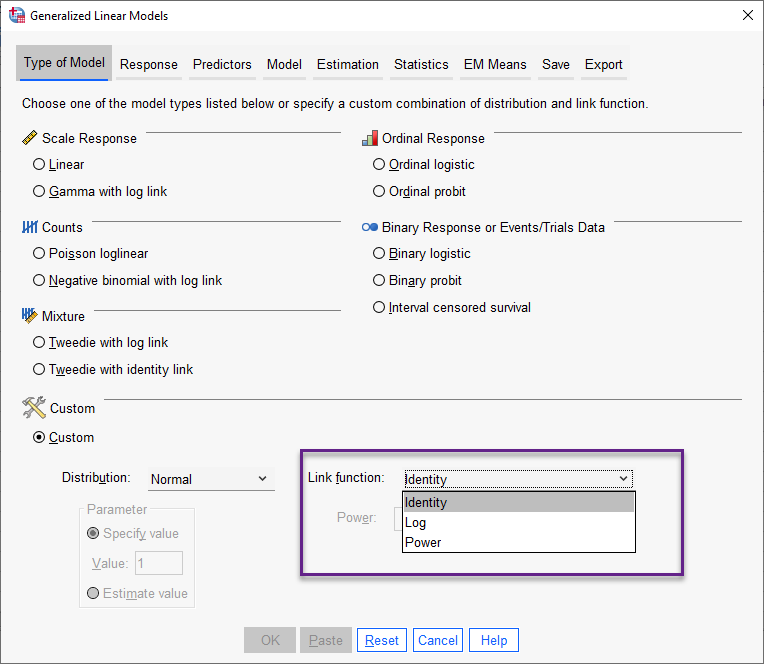
همان‌گونه که در تصویر بالا مشاهده می‌کنید، توابع پیوند در کادر Link function پنجره Type of model قرار دارند. در زمینه انواع توابع پیوند علاقمند بودید می‌توانید این لینک را ببینید.

هنگامی که ما گزینه‌ی Linear را انتخاب می‌کنیم، به صورت پیش‌فرض نرم‌افزار تابع پیوند Identity را برای داده‌های ما قرار می‌دهد و همان‌گونه نیز که گفتم این گزینه بر روی داده‌های عددی دارای توزیع نرمال، انتخاب می‌شود.

هنگامی که توزیع داده‌های پاسخ از نوع گاما باشد، از این مدل استفاده می‌کنیم. این مدل بر روی داده‌های فقط مثبت (بزرگتر از صفر) که به سمت داده‌های مثبت بزرگ چوله هستند، اجرا می‌شود. معمولاً از این مدل که می‌توان آن را رگرسیون گاما Gamma Regression نیز نامید، در مطالعات مربوط به بیمه و بازرگانی استفاده می‌شود. همچنین از این مدل در مطالعات پزشکی مربوط به بیماری‌های نادری که سری زمانی رخداد آن‌ها پراکنده است، استفاده می‌شود. در این لینک می‌توانید توضیحاتی درباره‌ی فرمول و تئوری توزیع گاما مشاهده کنید.

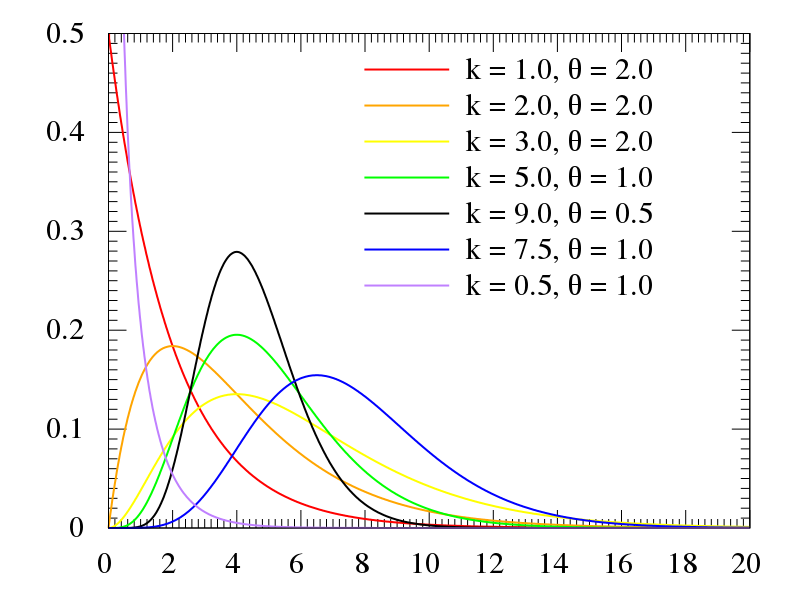
در تصویر زیر می‌توانید چند گراف با تابع احتمال توزیع گاما را مشاهده کنید. داده‌ها در توزیع گاما به شکل‌های زیر می‌توانند پراکنده شوند. این گراف‌ها همگی توزیع گاما با پارامترهای مختلف هستند.

در تصویر زیر می‌توانید یک مدل رگرسیون گاما بر روی داده‌های فرضی را مشاهده کنید. در واقع هنگامی که نمودار پراکنش ما به صورت زیر باشد، انتخاب مدل Gamma می‌تواند بهترین گزینه باشد.

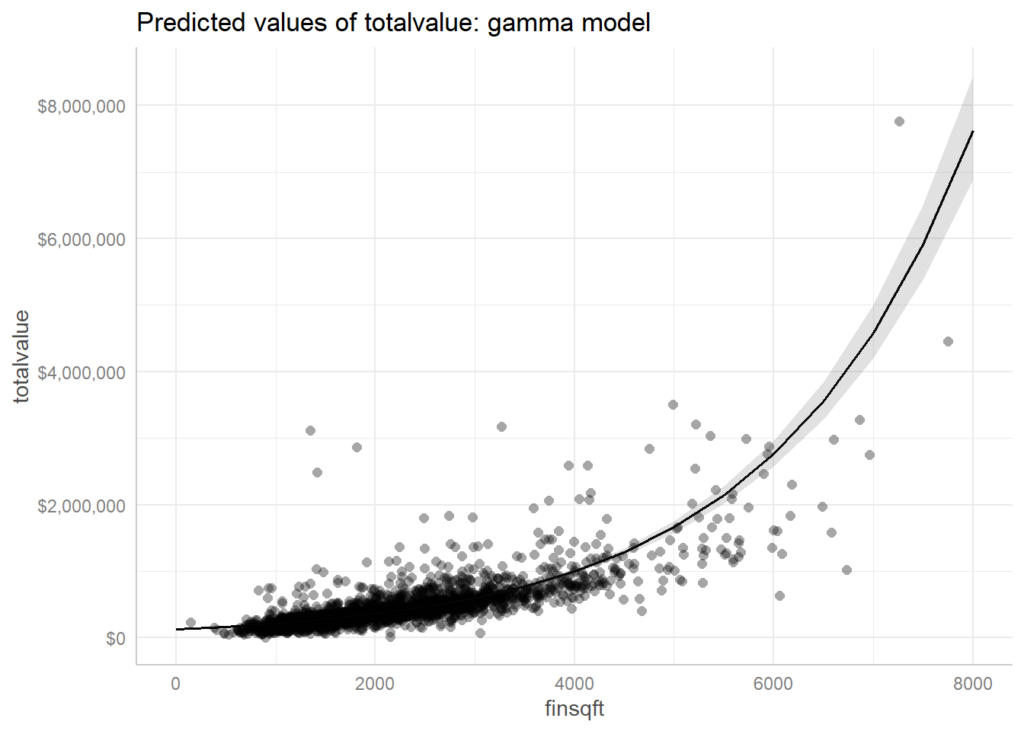
نکته دیگر اینکه انتخاب گزینه Gamma در کادر Linear Response سبب می‌شود تابع پیوند یا همان Link function به صورت log link تعریف شود. توضیح این‌که تابع پیوند از نوع log link به صورت تابع $ \displaystyle f\left( x \right)=\log \left( x \right)$ تعریف می‌شود. به معنای اینکه هنگام استفاده از گزینه Gamma، داده‌های کمیت پاسخ به لگاریتم خود تبدیل می‌شوند و سپس آنالیز بر روی داده‌های لگاریتمی انجام می‌شود.

 2. Ordinal Response  هنگامی که کمیت پاسخ مطالعه رتبه‌ای و ترتیبی Ordinal باشد از مدل‌های موجود در این بخش استفاده می‌کنیم. این مدل‌ها به صورت زیر هستند.

مثال‌های زیادی از مدل‌های رگرسیون ترتیب می‌توان بیان کرد. به عنوان مثال من در این و این مقاله به توضیح آن‌ها پرداخته‌ام. به عنوان مثال در مطالعه‌ای که کمیت پاسخ آن تحت عنوان رضایت و به صورت رتبه‌بندی است، می‌توان از این مدل استفاده کرد. در این گزینه، تابع پیوند تحت عنوان Cumulative logit تعریف می‌شود. این تابع به صورت $ \displaystyle f\left( x \right)=\ln \left( {\frac{x}{{1-x}}} \right)$ بیان می‌شود. خوب است این نکته را بدانیم که این تابع پیوند فقط برای کمیت‌های پاسخ رتبه‌ای و چندجمله‌ای Multinomial مناسب است. علاقمند بودید درباره‌ی مدل رگرسیون چند‌جمله‌ای این لینک را ببینید.

در این گزینه نیز توزیع و Measure داده‌های پاسخ به صورت ترتیبی و رتبه‌ای است. با این حال تفاوت آن با گزینه‌ی قبلی این است که تابع پیوند در این گزینه Cumulative probit تعریف می‌شود. این تابع به صورت $\displaystyle f\left( x \right)={{\Phi }^{{-1}}}\left( x \right)$ بیان می‌شود. که در آن $ \displaystyle {{\Phi }^{{-1}}}$ تحت عنوان وارون تابع توزیع تجمعی نرمال استاندارد، تعریف می‌شود. به بیان ساده اینکه با انتخاب این گزینه داده‌های کمیت پاسخ به داده‌های مبتنی بر معکوس توزیع تجمعی نرمال خود، تبدیل می‌شوند.

علاقمند بودید درباره‌ی مدل رگرسیون پروبیت این لینک را ببینید. من در سایت گراف پد درباره‌ی آن چند مقاله نوشته‌ام. در اینجا نیز بیان می‌کنیم که این تابع پیوند فقط برای کمیت‌های پاسخ رتبه‌ای و چندجمله‌ای Multinomial مناسب است.

 3. Counts  هنگامی که کمیت پاسخ مطالعه از نوع فراوانی، شمارش و تعداد باشد از مدل‌های موجود در این بخش استفاده می‌کنیم. این مدل‌ها به صورت زیر هستند.

این یک مدل رگرسیون غیرخطی با نام رگرسیون پواسن Poisson Regression است و هنگامی استفاده می شود که پدیده مورد بررسی خود دارای توزیع آماری پواسن Poisson Distribution باشد. داده‌های این مدل باید غیر منفی (صفر و بزرگتر) باشند. توزیع پواسون را می توان به عنوان تعداد وقوع رویداد مورد علاقه در یک دوره زمانی ثابت در نظر گرفت. مثال‌های توزیع پواسن را می‌تواند تعداد نقص‌ها در یک سیستم تولیدی، تعداد تصادفات، تعداد افراد مبتلا به یک بیماری خاص و یا تعداد بازدیدکنندگان یک وب سایت در هر ساعت باشد. درباره‌ی مدل رگرسیون پواسن می‌توانید این لینک را در سایت گراف پد ببینید.

تابع پیوند در این گزینه از نوع log به صورت $ \displaystyle f\left( x \right)=\log \left( x \right)$ تعریف می‌شود. به معنای اینکه داده‌های کمیت پاسخ که دارای توزیع پواسن هستند، به لگاریتم خود تبدیل می‌شوند و سپس آنالیز بر روی داده‌های لگاریتمی انجام می‌شود. خوب است این نکته را بدانیم که تابع پیوند log link می‌تواند بر روی داده‌های هر نوع توزیعی اجرا شود.

هنگامی که داده‌های پاسخ دارای توزیع دو جمله‌ای منفی باشند، از این گزینه استفاده می‌کنیم. این توزیع را می‌توان به عنوان تعداد آزمایش‌های مورد نیاز برای مشاهده k موفقیت در نظر گرفت و برای داده‌های با مقادیر صحیح غیر منفی (صفر و بزرگتر) مناسب است. داده‌های توزیع دوجمله‌ای منفی فقط می‌توانند دو نتیجه داشته باشند، یکی موفقیت و دیگری شکست. آنچه که در مطالعه و تحلیل نیز قرار می‌گیرد، تعداد تکرارها و آزمایش‌ها جهت رسیدن به تعداد مشخصی موفقیت است. این یک نکته کلیدی و تمایز استفاده از مدل رگرسیون دوجمله‌ای منفی از مدل رگرسیون پواسن است.

توزیع دوجمله‌ای منفی در مطالعات مالی، مهندسی و زیست شناسی کاربردهای متنوعی دارد. به عنوان مثال مدل‌سازی تعداد معوقات وام قبل از انجام تعداد معینی از پرداخت‌ها و یا مدل‌سازی تعداد عیوب در یک محصول تولیدی قبل از تولید تعداد معینی از محصولات.

هنگامی که Negative binomial with log link را انتخاب می‌کنیم، مقدار عددی پارامتر این توزیع به صورت پیش‌فرض، یک (1) در نظر گرفته می‌شود. چنانچه بخواهیم پارامترهای توزیع را به دلخواه و مبتنی بر داده‌های خود قرار دهیم، این کار را می‌توانیم با استفاده از کادر Custom در پایین پنجره Type of Model انجام دهیم. تصویر زیر را ببینید.

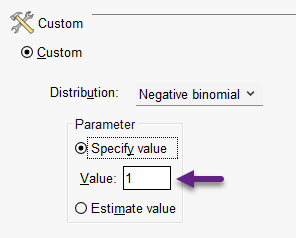
چنانچه از نرم‌افزار بخواهیم پارامتر توزیع را برای ما براورد کند، گزینه‌ی Estimate value را انتخاب می‌کنیم. خوب است این نکته را بدانید هنگامی که عدد پارامتر صفر (0) تنظیم شود، استفاده از این توزیع معادل استفاده از توزیع پواسون خواهد بود.

تابع پیوند در این گزینه از نوع log link به صورت $ \displaystyle f\left( x \right)=\log \left( x \right)$ تعریف می‌شود. به معنای اینکه داده‌های کمیت پاسخ، به لگاریتم خود تبدیل می‌شوند و سپس آنالیز بر روی داده‌های لگاریتمی انجام می‌شود.

 4. Binary Response or Events/Trials Data  هنگامی که داده‌های کمیت پاسخ به صورت باینری (صفر و یک) باشند از مدل‌های موجود در این بخش استفاده می‌کنیم. این مدل‌ها به صورت زیر هستند.

احتمالاً با این مدل رگرسیونی آشنا هستید. مدل رگرسیون باینری لجستیک هنگامی که Dependent Variable از نوع باینری باشد، به وفور مورد استفاده قرار می‌گیرد. در این لینک سایت گراف پد می‌توانید با آن به صورت کامل آشنا شوید.

تابع پیوند در این مدل به صورت logit یعنی $ \displaystyle f\left( x \right)=\log \left( {\frac{x}{{1-x}}} \right)$ تعریف می‌شود.

در اینجا نیز داده‌ها به صورت باینری هستند. تفاوت آن با گزینه قبلی در تابع پیوند آن است. link function در اینجا به صورت پروبیت و با فرمول $\displaystyle f\left( x \right)={{\Phi }^{{-1}}}\left( x \right)$ بیان می‌شود. که در آن $ \displaystyle {{\Phi }^{{-1}}}$ تحت عنوان وارون تابع توزیع تجمعی نرمال استاندارد، تعریف می‌شود.

در سایت گراف پد و در لینک رگرسیون پروبیت باینری در مسیر مدل‌های خطی تعمیم یافته، آموزش همین گزینه را مشاهده کنید. علاقمند بودید این لینک را هم ببینید.

این گزینه هنگامی انتخاب می‌شود که ما با آنالیز بقا در داده‌های خود روبه‌رو باشیم. معمولاً بازه بقا سانسورشده، هنگامی استفاده می‌شود که رخ دادن پیشامد مورد علاقه (Event) قابل مشاهده نیست و تنها می‌دانیم که در یک بازه زمانی رخ داده است. در این زمینه علاقمند بودید می‌توانید این مقاله را بخوانید.

همچنین در موضوع مفاهیم اساسی آنالیز بقا می‌توانید این لینک و آموزش کامل آن را در این لینک سایت گراف پد مشاهده کنید.

تابع پیوند در مدل بازه بقا سانسور شده به صورت Complementary log-log یعنی تابع $ \displaystyle f\left( x \right)=\log \left( {-\log \left( {1-x} \right)} \right)$ تعریف می‌شود.

 5. Mixture  همان‌گونه که از نام این بخش برمی‌آید، مدل‌های موجود در آن هنگامی که داده‌های کمیت پاسخ دارای توزیع آمیخته Mixture باشند مورد استفاده قرار می‌گیرد. داده‌ها در این مدل‌ها از ترکیب توزیع‌های پواسن و گاما ساخته می‌شوند.

این ترکیب سبب می‌شود بتوانیم داده‌های فقط مثبت و در عین حال وجود احتمال بزرگتر از صفر در مقدار ثابت صفر را نیز داشته باشیم. بنابراین در این مدل‌ها، کمیت پاسخ می‌تواند صفر نیز باشد (فقط منفی نباید باشد). مقدار ثابت پارامتر توزیع تویدی Tweedie می تواند هر عددی بزرگتر از یک و کوچکتر از دو باشد. در واقع در داده‌هایی که فراوانی زیادی در اطراف صفر و تعداد معدودی دیتا با اندازه خیلی بزرگ داریم، مدل‌های رگرسیون Tweedie‌ می‌تواند مفید باشد.

این مدل‌ها به صورت زیر هستند.

در این حالت مدل تویدی دارای تابع پیوند لگاریتمی به صورت $ \displaystyle f\left( x \right)=\log \left( x \right)$ تعریف می‌شود.

در این حالت تابع پیوند مدل به صورت Identity یعنی به صورت $ \displaystyle f\left( x \right)=x$ تعریف می‌شود.

در زمینه کاربرد مدل‌های Tweedie خوب است این مطلب را بدانیم که مدل‌سازی داده‌های هزینه بهداشتی به دلیل ماهیت چوله به راست این داده‌ها و وجود تعداد زیاد داده‌های نزدیک به صفر، دشوار است. یک راه‌حل رایج برای مدل‌سازی داده‌های هزینه، استفاده از مدل گاما در GLM است که می‌تواند به ماهیت چوله به راست توزیع بپردازد. با این حال، محدودیت‌هایی برای مدل گاما وجود دارد، به‌ویژه وقتی صحبت از هزینه‌های صفر به میان می‌آید. به دلیل اینکه توزیع گاما به داده‌های بزرگتر از صفر می‌پردازد.

راه‌حل جایگزین استفاده از چارچوب مدل Tweedie GLM است که در آن می‌توانیم به دلیل وجود ترکیب توزیع گاما با پواسن، جهت حل مسئله هزینه‌های صفر استفاده کنیم. در این مثال استفاده از مدل‌های Tweedie سبب می‌شود بتوانیم به طور همزمان احتمال نتیجه صفر، یعنی عدم استفاده از مراقبت‌های بهداشتی و هزینه‌های مستمر برای کاربران خدمات بهداشتی را مدل‌سازی کنیم. یک مثال خوب می‌تواند این مقاله باشد. علاقمند بودید آن را ببینید.

گراف زیر که من آن را رسم کرده‌ام، هیستوگرام داده‌های دارای توزیع Tweedie است. هنگامی که با چنین داده‌هایی روبه‌رو هستیم که فراوانی زیادی در اطراف نقطه صفر قرار گرفته است و بقیه داده‌ها دارای توزیع گاما، چوله به راست هستند، بهترین گزینه همین مدل Tweedie می‌باشد.

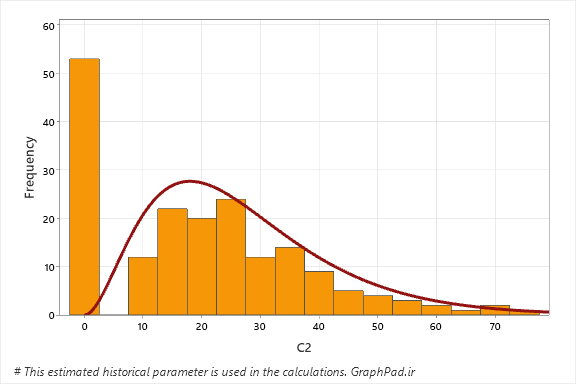
 6. Custom  حال اگر خودمان ایده‌ای داشته باشیم که داده‌های پاسخ ما دارای توزیع خاصی است و بخواهیم تابع پیوند دیگری بر روی داده‌ةا تعریف کنیم، نرم‌افزار SPSS این امکان را در بخش Custom قرار داده است تا بتوانیم بر مبنای ایده‌ی خود، توزیع و تابع پیوند خاصی را انتخاب کنیم.

در تصویر زیر می‌توانید توابع پیوند و توزیع‌های موجود را مشاهده کنید.

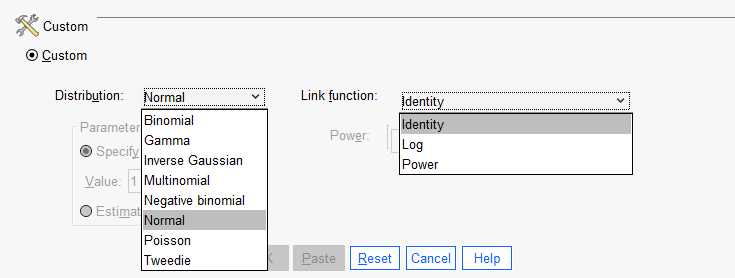
.یک توضیح کوتاه اینکه تابع پیوند Power به صورت $ \displaystyle f\left( x \right)={{x}^{\alpha }}$ تعریف می‌شود.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2024). Types of generalized linear models in SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/types-of-generalized-linear-models-spss.php

For example, if you viewed this guide on 12^th January 2024, you would use the following reference

GraphPad Statistics (2024). Types of generalized linear models in SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/types-of-generalized-linear-models-spss.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.