مدل های آمیخته خطی Linear Mixed Models در نرم‌افزار SPSS

 Mixed Models 

در مدل‌های خطی Linear Model (LM) یا مدل‌های خطی تعمیم یافته General Linear Model (GLM) با دو مفهوم و دو سر رابطه روبه‌رو هستیم. یکی از آن‌ها کمیت وابسته یا همان Dependent Variable (DV) است و سمت دیگر رابطه با نام کمیت‌های مستقل یا همان Independent Variable (IV) نامیده می‌شود.

مطالعه این مقالات به شما کمک می‌کند که دریابید اثر ثابت و تصادفی چیست، به چه چیزی ثابت و یا تصادفی گفته می‌شود و همچنین نحوه آنالیز و بیان تحلیل‌های آنالیز واریانس با اثر تصادفی چگونه است. در این زمینه چنانچه علاقمند بودید خوب است مقاله (تحلیل مولفه های واریانس Variance Components) را هم بخوانید.

مدل خطی آمیخته، انعطاف‌پذیری مدل‌سازی نه فقط بر مبنای میانگین داده‌ها، بلکه بر مبنای واریانس‌ و کوواریانس‌های آنها را نیز فراهم می‌کند. در واقع باید بیان کرد که فهم مدل‌های آمیخته کمی پیچیده‌تر از سایر مدل‌های خطی آماری مانند آنالیز واریانس و یا کوواریانس است و نیاز به دانستن برخی مقدمات و تئوری‌های آماری دارد. من در لینک‌های بالا سعی کرده‌ام ابتدا به بیان این مقدمات بپردازم.

 

مثال مدل‌های آمیخته Mixed Models

 Example 

آشنایی با مدل‌های آمیخته را از یک مثال شروع می‌کنم. سعی کرده‌ام در این مثال اجزای تشکیل دهنده Mixed Model را قرار دهم. فهم این مثال کمک می‌کند درک درستی از مدل‌های آمیخته داشته باشیم و بتوانیم به تحلیل آن‌ها با استفاده از نرم افزار SPSS بپردازیم. پس از آن به بیان تئوری مدل‌های آمیخته خواهیم پرداخت.

فرض کنید یک موسسه آموزشی می‌خواهد به بررسی چند متد آموزشی و تاثیر این متدها بر نمره نهایی دانش‌آموزان در سطح کشور بپردازد. من اسم متدهای آموزشی را به اختصار A, B و C بیان می‌کنم. موسسه به دنبال بررسی اثرگزاری متدها مبتنی بر جنسیت دانش‌آموزان نیز بوده است، بنابراین یک فاکتور دیگر با نام جنسیت وارد مطالعه می شود. واضح است که تا این‌جا مثال ما آنالیز واریانس با اثرات ثابت (نوع متد و جنسیت دانش‌آموز) است که نام آن Two-way ANOVA است.

حال فرض کنید می‌خواهیم سطح سواد والدین دانش‌آموزان را نیز به عنوان یک کنترل‌کننده و Covariate وارد مطالعه کنیم. به این ترتیب هم‌زمان با دانش‌آموز، والدین او هم تحت پرسش قرار گرفته و برای آن‌ها نیز یک نمره به نام اندازه سواد به دست آمده است. بنابراین مطالعه ما به آنالیز کوواریانس دو طرفه با اثرات ثابت یعنی Two-way ANCOVA تبدیل می‌شود.

تا اینجا مطالعه ما فقط دارای اثرات ثابت است و در آن خبری از اثرات تصادفی نیست. با این حال باید به دو نکته مهم توجه شود. موسسه آموزشی نمی‌تواند همه‌ی مدارس کشور را بررسی کند. از طرف دیگر در هر مدرسه هم نمی‌تواند همه‌ی دانش‌آموزان را نیز مورد سنجش قرار دهد. بنابراین یک نمونه تصادفی از مدارس کشور و همچنین یک نمونه تصادفی از دانش‌آموزان هر مدرسه، انتخاب می‌شود. ورود این دو کمیت یعنی یکی نمونه تصادفی از مدارس و دیگری نمونه تصادفی از دانش‌آموزان هر مدرسه سبب می‌شود، مطالعه ما به Mixed Model که هم دارای اثر ثابت و هم اثر تصادفی است، تبدیل شود.

اجازه دهید یک بخش دیگر نیز به این مدل آمیخته اضافه شود و آن هم اینکه بررسی و ارزشیابی دانش‌آموز و والدین آن‌ها در پایان هر ماه تکرار می‌شود. یعنی به ازای هر فرد 7 نمره (این مطالعه در هفت ماه انجام شده است) وجود دارد.

در تصویر زیر بخشی از فایل دیتا این مثال را مشاهده می‌کنید. از اینجا می‌توانید داده‌ها و نتایج این مثال را دریافت کنید.

 

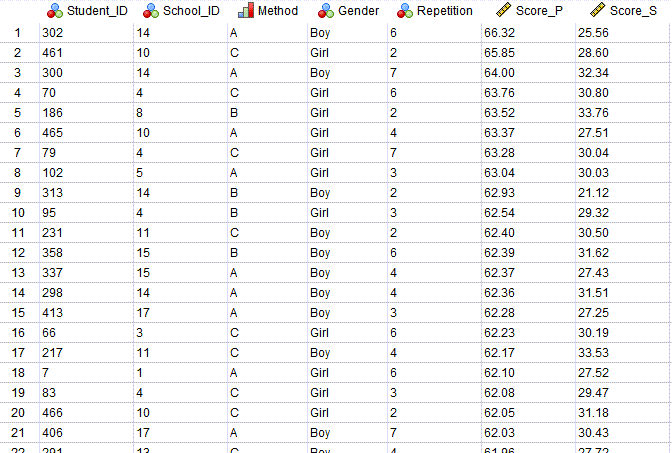
این مثال شامل بررسی 475 دانش‌آموز از 17 مدرسه در سراسر کشور است. از هر دانش‌آموز و والدین او نیز هفت بار آزمون گرفته شده و نمرات به دست آمده است. در ادامه من به تعریف هر ستون در فایل دیتا پرداخته‌ام.

Student_ID. در این ستون، شماره شناسایی هر کدام از دانش‌آموزان آمده است. این ستون، اعدادی از 1 تا 475 (تعداد دانش‌آموزان مورد مطالعه) را دارد.

School_ID. شماره شناسایی هر مدرسه در این ستون به صورت اعدادی از 1 تا 17 (تعداد مدارس مورد بررسی) نوشته شده است.

Method. روش و متد آموزشی مورد استفاده برای هر دانش‌آموز، اینجا نوشته شده است. این متدها به صورت کدهای A, B و C آمده است.

Gender. جنسیت دانش‌آموزان در این ستون دیده می‌شود.

Repetition. بیانگر شماره تکرار (از 1 تا 7) آزمون می‌باشد. عدد نوشته شده در این ستون نشان می دهد، نمره هر فرد مربوط به کدام تکرار آزمون بوده است.

Score_P. نمره به دست آمده به ازای والدین در هر بار تکرار، اینجا نوشته شده است.

Score_S. نمره به دست آمده دانش‌آموز در هر بار تکرار، اینجا نوشته شده است. این ستون به عنوان Dependent Variable مطالعه شناخته می‌شود.

همان‌گونه که بیان کردیم، هدف ما این است که دریابیم آیا متد آموزشی بر نمره به دست آمده دانش‌آموزان، اثرگزار است یا خیر. در این بررسی جنسیت دانش‌آموز، نوع متد و نمرات والدین به عنوان اثرات ثابت و شماره مدرسه به عنوان اثر ثابت وارد مدل خواهد شد.

نکته مهمی که در اینجا وجود دارد و ما در مقاله اثرات ثابت یا تصادفی هم به آن پرداختیم، این است هنگامی که ما فاکتوری را به عنوان اثر تصادفی در نظر می‌گیریم، از آن‌جا که این فاکتور، نمونه تصادفی از یک کل است و از آن کل به تصادف انتخاب شده است، بنابراین نتایج به دست آمده بر مبنای این فاکتور را می‌توانیم به آن مجموعه بزرگتر تعمیم دهیم. در واقع Random Factor این قابلیت را دارد که به مجموعه بزرگتری که از آن می‌آید، گسترش یابد. این مطلب در این مثال به معنای این است که ما نتایج به دست آمده از بررسی 17 مدرسه را می‌توانیم به همه‌ی مدارس تعمیم دهیم.

 

تئوری مدل‌های آمیخته

 Formulas 

مدل آمیخته این مثال را می‌توان به صورت زیر نوشت.

$ \displaystyle {{y}_{{ij}}}=\mu +{{\beta }_{1}}Metho{{d}_{{ij}}}+{{\beta }_{2}}Gende{{r}_{{ij}}}+{{\tau }_{i}}+{{\gamma }_{{ij}}}+{{\varepsilon }_{{ij}}}\begin{array}{*{20}{c}} {} \end{array}\left\{ {\begin{array}{*{20}{c}} {i=1,2,….,k} \\ {j=1,2,….,n} \end{array}} \right\}$

در این مدل، $ \displaystyle {{y}_{{ij}}}$ به عنوان اندازه عددی کمیت وابسته برای i امین مدرسه و j امین دانش‌آموز، $ \displaystyle \mu $ اثر ثابت، $ \displaystyle {{\tau }_{i}}$ اثر تصادفی i امین مدرسه و به تصادف انتخاب شده، $ \displaystyle {{\gamma }_{{ij}}}$ اثر تصادفی انتخاب j امین دانش‌آموز از مدرسه i ام و $ \displaystyle {{\varepsilon }_{{ij}}}$ خطای مطالعه برای i امین مدرسه و j امین نفر، می‌باشد.

 چند نکته 

خوب است در اینجا به چند نکته در زمینه شروع کار و تحلیل با مدل‌های آمیخته، اشاره کنم. ابتدا اینکه کمیت وابسته باید عددی Scale باشد. فاکتورها و مولفه‌های اثر ثابت و تصادفی لازم است گروه‌بندی Categorical در نظر گرفته شده باشند. کمیت‌های کمکی که به آن‌ها Covariate گفته می‌شود، باید کمی و عددی باشند. افراد و موضوعات که نرم‌افزار به آن‌ها Subjects می‌گوید و همچنین کمیت بیان کننده تکرار، می‌توانند از هر نوع اندازه‌گیری‌ها یعنی Nominal، Ordinal و یا Scale در نظر گرفته شوند.

در یک مدل آمیخته خطی Linear Mixed Model که در این مقاله درباره‌ی آن حرف می‌زنیم، Dependent Variable به صورت خطی با عوامل ثابت، تصادفی و کمیت‌های کمکی مرتبط فرض می‌شود. دانستن این موضوع مهم است که اثرات ثابت میانگین کمیت وابسته را مدل می‌کنند. اثرات تصادفی ساختار کوواریانس کمیت وابسته را مدل می‌کنند. چنانچه در یک مطالعه چندین اثر تصادفی داشته باشیم، آن‌ها مستقل از یکدیگر در نظر گرفته می‌شوند و ماتریس‌های کوواریانس جداگانه برای هر یک محاسبه می‌شود. به همین ترتیب تکرارها ساختار کوواریانس باقیمانده‌ها را مدل می‌کنند. Dependent Variable نیز دارای توزیع نرمال فرض می‌شود.

 

تنظیمات نرم‌افزار در مدل‌های آمیخته

 Setting 

حال بیایید به همان مثال بالا و بررسی اثرات ثابت و تصادفی فاکتورهای جنسیت، متد آموزشی، نمره والدین، مدرسه و دانش‌آموز بر روی نمره نهایی دانش‌آموزان، بپردازیم. از مسیر زیر در نرم‌افزار SPSS جهت تحلیل مدل‌های آمیخته به صورت خطی، استفاده می‌کنیم.

 Analyze → Mixed models → Linear  

در این صورت پنجره زیر با نام Linear Mixed Models: Specify Subjects and Repeated برای ما باز می‌شود.

 

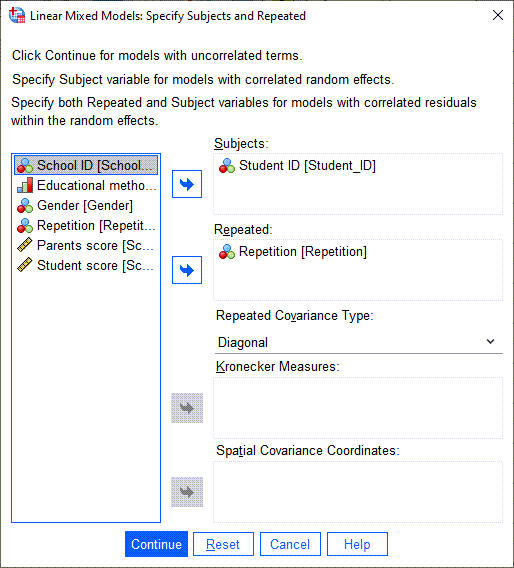
در کادر Subjects کمیت بیان کننده شماره شناسایی دانش‌آموزان یعنی Student_ID قرار می‌گیرد. در کادر Repeated نیز همان Variable نشان دهنده شماره تکرار آزمون با نام Repetition قرار گرفته است.

پنجره بالا به ما امکان می‌دهد افراد و تکرارها را در نرم‌افزار معرفی کنیم. البته انتخاب کمیت‌ها در ابن پنجره ضروری نیست و بدون آن‌ها نیز نرم‌افزار می‌تواند تحلیل آمیخته را انجام دهد. من در ادامه سعی کردم بیشتر درباره‌ی بخش‌های Subjects و Repeated صحبت کنم.

 Subjects  ابتدا بیایید درباره‌ی کادر Subjects حرف بزنیم.

یک Subject، یک واحد مشاهده است که می‌توان آن را مستقل از سایر Subject ها در نظر گرفت. آن‌ها افراد، نمونه‌ها و کیس‌های انسانی یا غیرانسانی هستند که مورد مطالعه قرار می‌گیرند. به عنوان مثال، عدد فشار خون از یک بیمار در یک مطالعه پزشکی را می‌توان مستقل از عدد سایر بیماران در نظر گرفت.

هنگامی که برای هر Subject، تکرار انجام می‌شود و می‌خواهید همبستگی بین مشاهدات را مدل‌سازی کنید، تعریف Subject ها اهمیت پیدا می‌کند. به عنوان مثال، ممکن است انتظار داشته باشید که فشار خون در یک بیمار، فقط در طول ویزیت‌های متوالی با هم مرتبط باشند.

نکته مهمی که در اینجا وجود دارد و من می‌خواهم به آن اشاره کنم این است که لازم نیست حتماً سابجکت‌ها به عنوان افراد و Case ها انتخاب شوند. ما می‌توانیم حتی آن‌ها را با فاکتورهای چند سطحی نیز تعریف کنیم. برای مثال، می‌توانیم جنسیت و رده‌های سنی را به‌عنوان Subject در نرم‌افزار، قرار دهیم. این کار سبب می‌شود بتوانیم این ایده را مدل کنیم که به عنوان مثال مردان بالای 65 سال شبیه یکدیگر هستند اما از مردان کمتر از 65 سال و زنان مستقل می‌باشند.

همه‌ی کمیت‌های قرار گرفته در کادر Subjects جهت طراحی ساختار کوواریانس باقیمانده Residual Covariance استفاده می‌شوند. همچنین می‌توانید از برخی یا همه‌ی آن‌ها برای طراحی ساختار کوواریانس اثرات تصادفی Random-Effects Covariance نیز استفاده کنید.

 Repeated  چنانچه Subject های ما دارای تکرار باشند، یعنی هر کدام چندین بار در تایم‌ها یا وضعیت‌های مختلف، اندازه‌گیری شده باشند، در این کادر Variable بیان‌کننده تکرار را قرار می‌دهیم. برای مثال کمیتی با نام Week می‌تواند در یک مطالعه تعریف شود و مقادیر به دست آمده برای 10 هفته مشاهدات را در یک تحقیق پزشکی مشخص کند. در این صورت ما کمیت Week را در این کادر قرار می‌دهیم.

در پنجره بالا بخش‌های دیگری به عنوان مثال Repeated Covariance Type دیده می‌شود. با استفاده از گزینه‌های مختلف این بخش می‌توانیم ساختار کوواریانس باقیمانده‌ها را انتخاب کنیم. در این زمینه و همچنین سایر بخش‌های پنجره بالا علاقمند بودید این لینک را ببینید.

هنگامی که در پنجره Specify Subjects and Repeated که می‌توان آن را پنجره ورود به تحلیل مدل‌های آمیخته دانست، کمیت‌های مناسب را تعریف می‌کنیم، Continue کرده و وارد پنجره Linear Mixed Models می‌شویم. در تصویر زیر آن را می‌بینید.

 

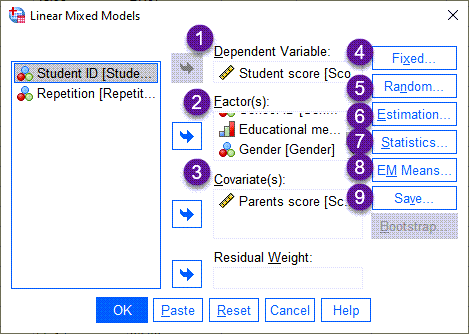
من پنجره تنظیمات بالا را شماره‌گزاری کرده‌ام و به ترتیب به توضیح هر کدام می‌پردازم.

 1  در کادر Dependent Variable که همان کمیت وابسته مطالعه است، ستون Student score یعنی نمرات آزمون هر فرد، قرار می‌گیرد.

 2  در کادر Factor(s) فاکتورهای مطالعه اعم از ثابت یا تصادفی، قرار می‌گیرند. نوع متد آموزشی، جنسیت و شماره شناسایی مدرسه در این بخش قرار گرفته است.

 3  این مطالعه دارای یک کووریت یعنی نمرات والدین هر دانش‌آموز نیز می‌باشد. به همین دلیل Parents score در کادر Covariate(s) قرار می‌گیرد.

 4  از اینجا به بعد وارد تب‌ها و آپشن‌های مختلف تنظیمات مدل‌های آمیخته خواهیم شد. در تب می‌توانیم مدل مبتنی بر فاکتورهای اثر ثابت را به نرم‌افزار بدهیم. در تصویر زیر این تب آمده است.

 

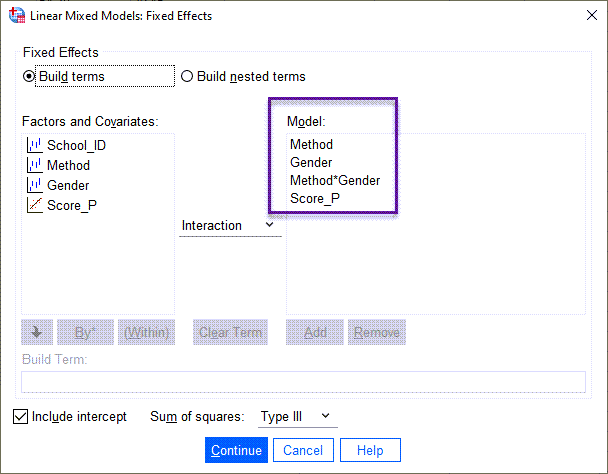
من در این تب از نرم‌افزار SPSS خواسته‌ام فاکتورهای دارای اثر ثابت جنسیت، متد آموزشی و نمره والدین را به صورت اثرات اصلی Main Effect و اثر متقابل بین جنسیت و متد را به صورت Interaction Effect وارد مدل اثر ثابت کند. در زمینه سایر تنظیمات این پنجره و به ویژه ساختن فاکتورهای آشیانه‌ای Nested Terms علاقمند بودید این لینک را ببینید.

 5  همان‌گونه که قبلاً بیان کردیم یک مدل آمیخته دارای دو بخش اثرات ثابت و اثرات تصادفی است. در تب می‌توانیم مدل مبتنی بر فاکتورهای اثر تصادفی را به نرم‌افزار بدهیم. در تصویر زیر این تب آمده است.

 

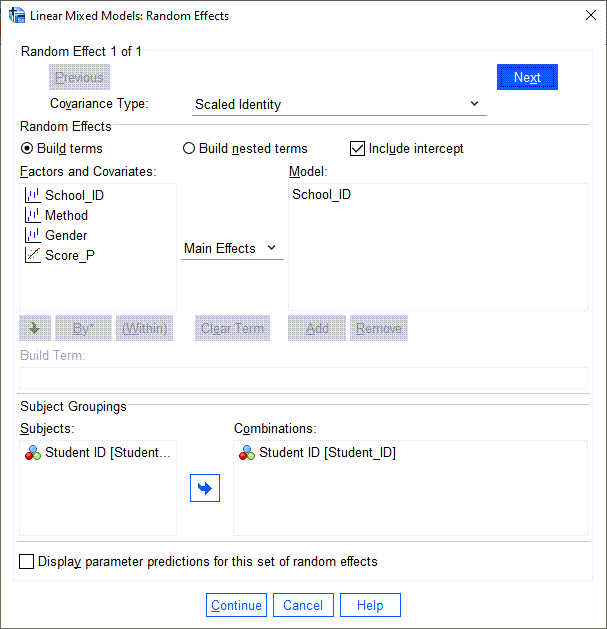
در پنجره Random Effects و در بخش Covariance Type گزینه‌ی Scaled Identity انتخاب شده است. این بخش به ما امکان می‌دهد ساختار کوواریانس را برای مدل اثرات تصادفی مشخص کنیم. گزینه‌ی Scaled Identity که من آن را انتخاب کرده‌ام دارای ساختار واریانس ثابت است. در این ساختار فرض بر این است که ارتباطی بین هیچ یک از فاکتورها وجود ندارد. علاقمند بودید درباره‌ی سایر گزینه‌ها و توضیح آن‌ها این لینک را ببینید.

در کادر Random Effects فاکتورهای اثر تصادفی را در مدل قرار می‌دهیم. در این مثال فاکتور School_ID را در قسمت Model گذاشته‌ام. همچنین گزینه‌ی Intercept را نیز انتخاب کرده‌ام. چنانچه بخواهید چندین مدل اثر تصادفی بسازید، روی Next کلیک کنید تا مدل بعدی ساخته شود. پس از آن می‌توانید روی Previous کلیک کنید تا مدل‌های موجود به عقب برگردد. هر مدل اثر تصادفی مستقل از مدل اثر تصادفی دیگر است. یعنی برای هر کدام ماتریس‌های کوواریانس جداگانه محاسبه خواهد شد.

بخش دیگر پنجره بالا با نام Subject Groupings گفته می‌شود. من در اینجا کمیت شماره شناسایی دانش‌آموزان را در کادر Combinations قرار داده‌ام. به خاطر داشته باشید این همان Variable ای بود که در پنجره ابتدایی و شروع تحلیل مدل‌های آمیخته آن را به عنوان Subjects در نرم‌افزار معرفی کردیم.

 6  در تب تنظیمات براورد پارامترهای مدل آمیخته، قرار دارد. در تصویر زیر این تب آمده است.

 

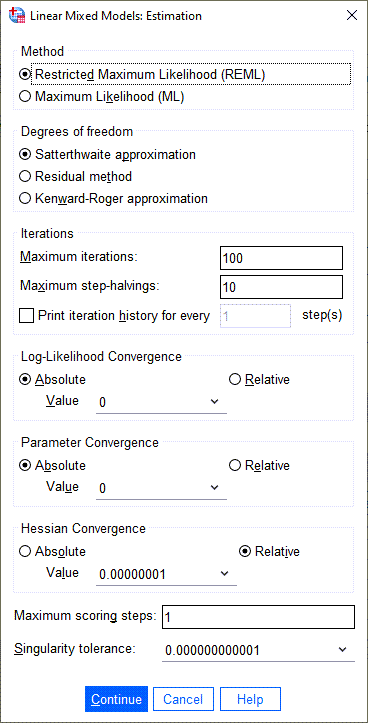
تنظیمات این تب معمولاً به صورت پیش‌فرض نرم‌افزار است و ما کاری با آن‌ها نداریم. علاقمند بودید در این لینک می‌توانید چیزهای بیشتری درباره‌ی این تب و گزینه‌های مختلف آن بدانید.

 7  در تب آماره‌های خروجی و قابل نمایش در نتایج مدل آمیخته، قرار دارد. در تصویر زیر این تب آمده است.

من در این تب گزینه‌های مختلفی را جهت نمایش آماره‌های توصیفی و براورد نتایج مدل آمیخته انتخاب کرده‌ام. انتخاب این گزینه‌ها به دلخواه انجام می‌شود. درباره‌ی گزینه‌های مختلف تب بالا، این لینک را ببینید. بعداً و به هنگام به دست آمدن نتایج در خروجی‌های نرم‌افزار SPSS درباره‌ی این گزینه‌ها بیشتر صحبت می‌کنیم.

 8  در تب می‌توانیم میانگین‌های حاشیه‌ای به ازای هر کدام از سطوح فاکتورهای دارای اثر ثابت را به دست آوریم. همچنین در اینجا و با انتخاب گزینه‌ی Compare main effects این امکان وجود دارد که به مقایسه‌ی گروه‌های مختلف اثرات اصلی با یکدیگر بپردازیم. با نوشتن Syntax در محیط برنامه‌نویسی نرم‌افزار SPSS می‌توانیم به مقایسه‌ی گروه‌های مختلف اثرات متقابل با یکدیگر هم بپردازیم. در این زمینه این لینک و این لینک در سایت گراف پد را ببینید.

 

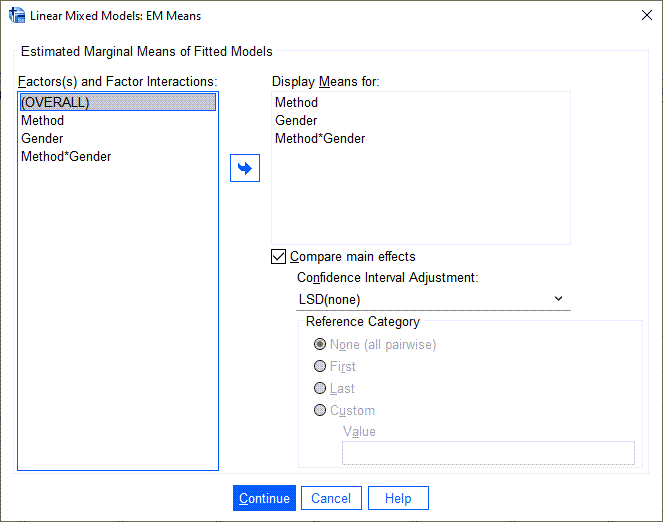
در تصویر بالا پنجره EM Means آمده است. من از نرم‌افزار خواسته‌ام برای جنسیت، متد آموزشی و اثر متقابل بین آن‌ها میانگین‌های حاشیه‌ای Marginal Means را به دست آورد. همچنین به مقایسه بین میانگین‌های حاشیه‌ای نمرات دانش‌آموزان در بین دختر و پسر و متدهای آموزشی بپردازد.

مقایسه بین گروه‌ها می‌تواند بر مبنای روش LSD بدون تعدیل و یا روش‌های بونفرونی و Sidak همراه با تعدیل Adjustment انجام شود. تصحیح بونفرونی و یا Sidak برای کاهش شانس به دست آوردن نتایج مثبت کاذب (خطای نوع اول) یعنی رد فرض صفر در صورتی که فرض صفر درست است، استفاده می‌شود. این کار به ویژه هنگامی که تعداد مقایسه‌های دوگانه زیاد است، توصیه می‌شود.

 9  چنانچه بخواهیم برخی از نتایج و خروجی‌های نرم‌افزار را در فایل دیتا و به ازای هر فرد مشاهده کنیم، گزینه‌های تب این کار را برای ما انجام می‌دهند. در تصویر زیر این تب آمده است.

 

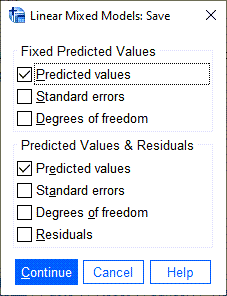
به عنوان مثال من در تب بالا از نرم‌افزار خواسته‌‌ام مقادیر پیش‌بینی خود از کمیت وابسته یعنی نمره دانش‌آموز را بر مبنای مدل اثر ثابت (بدون اثرات تصادفی) و همچنین بر مبنای مدل آمیخته (شامل اثرات ثابت و تصادفی) به دست آورد. در ادامه خواهیم دید که این انتخاب سبب می‌شود در فایل دیتا ستون‌های جدیدی ایجاد شود و مقادیر برازش شده نمره به ازای هر فرد در هر تکرار آزمون را به ما نشان دهد. در این زمینه می‌توانید این لینک را ببینید.

 

نتایج و خروجی‌های نرم‌افزار

 Results 

حال OK کنید. در این صورت می‌توانید نتایج و خروجی‌های نرم‌افزار SPSS در آنالیز مدل‌های آمیخته را مشاهده کنید. در ابتدا جدول زیر با نام Case Processing Summary مشاهده می‌شود. این یک جدول طولانی است که من بخش‌هایی از آن را در تصویر زیر آورده‌ام.

 

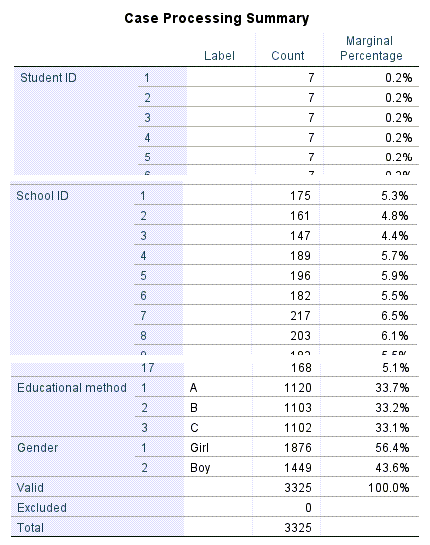
در این جدول تعداد فراوانی و درصد هر کدام از سطوح و گروه‌های Variable های مطالعه، آمده است. با استفاده از نتایج این جدول به عنوان مثال می‌توانیم دریابیم در هر گروه آموزشی چند نفر بوده است و یا در هر مدرسه چند دانش‌آموز به تصادف انتخاب شده است.

جدول بعدی نتایج نیز با نام Descriptive Statistics مشاهده می‌شود. من بخش‌هایی از این جدول را در تصویر زیر آورده‌ام.

 

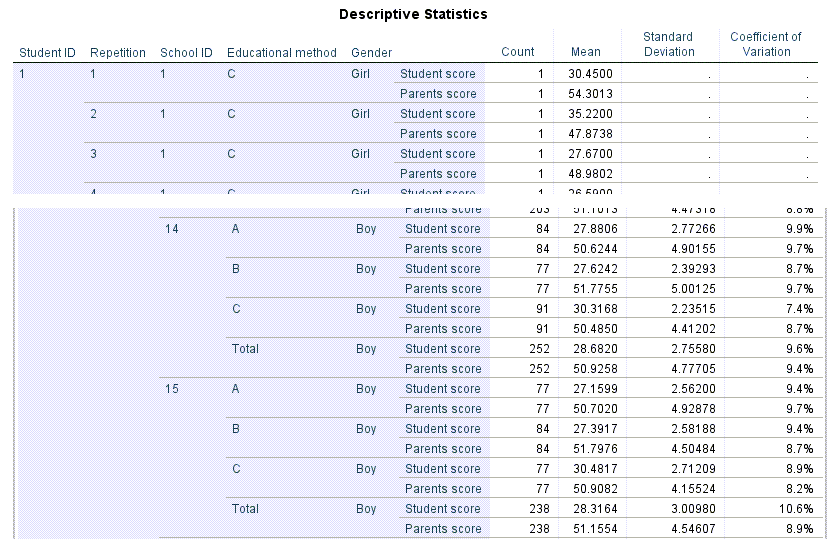
در این جدول می‌توانید آماره‌های توصیفی شامل میانگین، انحراف معیار و ضریب پراکندگی Coefficient of Variation، به ازای هر کدام از سطوح کمیت‌ها را مشاهده کنید. به عنوان مثال می‌توانیم آماره‌های توصیفی میانگین و انحراف معیار نمرات دانش‌آموزان در بین دختران مدرسه شماره 7 و متد آموزشی A که برابر با 24.48 و 2.19 شده است را به دست بیاوریم.

جدول دیگر با نام Model Dimension که به آن ابعاد مدل می‌گوییم در تصویر زیر آن را می‌بینید.

 

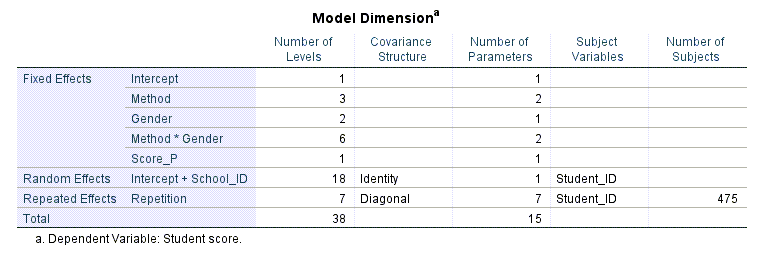
این جدول خلاصه‌ای از مدل آمیخته را نشان می‌دهد. مدل ما اثرات ثابت که شامل متد، جنسیت، اثر متقابل جنسیت و متد و نمره والدین دانش‌آموز و همجنین اثر تصادفی شماره مدرسه (مدارس به تصادف انتخاب شده‌اند) را ارایه می‌دهد. برای هر اثر، تعداد سطوح اثر و تعداد پارامترهای در نظر گرفته شده توسط اثر در مدل آمیخته، گزارش شده است. ساختار کوواریانس و کمیت‌هایی که افراد و تکرارها را تعریف می‌کنند، در جدول بالا بیان شده است.

در نتایج نرم‌افزار، جدول دیگری با نام Information Criteria که به آن معیارهای اطلاع می‌گوییم، دیده می‌شود. در تصویر زیر آن را ببینید.

 

ما از نتایج این جدول به منظور مقایسه‌ی بین چند مدل با یکدیگر استفاده می‌‌کنیم. شاخص‌هایی مانند -2 (Restricted) Log Likelihood، شاخص اطلاع آکائیک (AIC) و معیار بیزی شوارتز (BIC) از جمله مواردی هستند که در این جدول آمده‌اند. معمولاً بیان می‌شود مدلی که این شاخص‌ها در آن کمتر باشد، در مقایسه با مدل دیگر بهتر است.

البته ما در اینجا ابزاری در اختیار داریم تا بتوانیم دریابیم آیا مدل به صورت معنادار بهتر است یا با مدل دیگر تفاوتی ندارد. برای انجام این کار لازم است اختلاف عددی -2 (Restricted) Log Likelihood بین مدل‌ها به دست بیاید. پس از آن عدد به دست آمده را با آماره توزیع کای اسکوئر Chi square با تعداد درجات آزادی برابر با اختلاف تعداد پارامترهای براورد شده مدل‌ها، مقایسه کنیم. در این صورت اگر آماره توزیع کای اسکوئر عددی بیشتر از اختلاف لگاریتم نسبت درستنمایی باشد، می‌گوییم مدل‌ها با یکدیگر اختلاف معنادار ندارند و اگر Chi square عدد کمتری را نشان دهد، می‌گوییم مدل‌ةا با هم اختلاف معناداری دارند و آن مدلی بهتر است که معیارهای اطلاع در آن کوچکتر باشد.

جدول مهم دیگر در خروجی‌های نرم‌افزار، جدول Fixed Effects است. من در تصویر زیر آن را آورده‌ام.

 

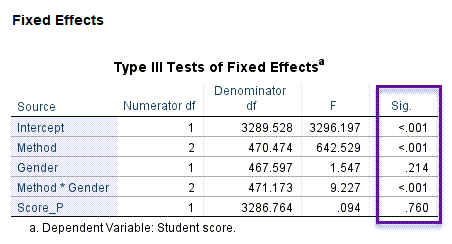
این جدول به بررسی تاثیر فاکتورهای اثر ثابت بر روی کمیت وابسته مطالعه یعنی نمره دانش‌آموزان، می‌پردازد. بر مبنای این نتایج در می‌یابیم که جنسیت تاثیر معنادار بر نمره آزمون ندارد (P-value = 0.214). با این حال متد آموزشی (P-value < 0.001) و اثر متقابل جنسیت و متد (P-value < 0.001) بر نمره آزمون تاثیر معنادار دارد. همچنین به دست آورده‌ایم که نمره والدین و سطح سواد آن‌ها بر نمره دانش‌آموزان تاثیر معنادار ندارد (P-value = 0.760). به این نکته توجه کنید که در این جدول از آزمون F استفاده شده است.

از جدول‌های پرکاربرد در مدل‌های آمیخته جدول زیر با نام Estimates of Fixed Effects است. این جدول به ما کمک می‌کند تا بتوانیم به مقایسه نمرات دانش‌آموزان در بین سطوح و گروه‌های مختلف فاکتورهای اثر ثابت با یکدیگر بپردازیم. مثلاً بتوانیم دختران را با پسران و یا متد آموزشی A را با C مقایسه کنیم. جدول زیر را ببینید.

 

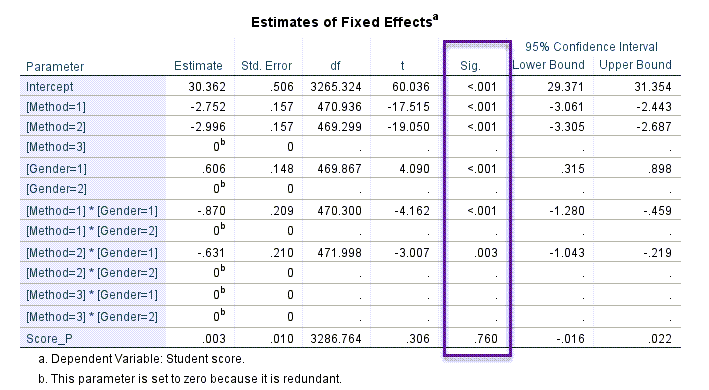
همان‌گونه که از جدول بالا دیده می‌شود، در هر اثر، یکی از گروه‌ها به عنوان رفرنس قرار گرفته می‌شود و بقیه گروه‌ها با آن مقایسه می‌شوند. به عنوان مثال براورد Estimate منفی به دست آمده برای متد A و B نشان می‌دهد، متد C دارای نمرات بیشتری نسبت به این متدها بوده است. این بیشتر بودن نیز معنادار به دست آمده است. به این نکته توجه کنید که در این جدول از آزمون t استفاده شده است.

برای جنسیت، پسران به عنوان رفرنس قرار گرفته است. عدد مثبت براورد شده برای دختران نشان می‌دهد، دختران دارای نمرات آزمون بالاتری نسبت به پسرها بوده‌اند. جالب توجه است که در این‌جا مقایسه معنادار به دست آمده است (P-value < 0.001). دلیل این مطلب را می‌توان تفاوت در نوع آزمون‌ها (یکی آزمون F و دیگری آزمون t دانست). دلیل دیگر وجود اثرات متقابل در مطالعه است. اگر ما مدل آمیخته‌ای بدون وجود اثر متقابل بین جنسیت و متد، بر این داده‌ها برازش دهیم، می‌توانیم مشاهده کنیم که جنسیت همانند جدول بالا معنادار نخواهد بود.

همچنین در جدول بالا مقایسه اثرات متقابل با یکدیگر نیز انجام شده است. در این جدول مقادیری که عدد ستون Estimate برای آن‌ها صفر در نظر گرفته شده است، به عنوان رفرنس و مقایسه با سایر گروه‌ها، قرار می‌گیرند.

در جدول زیر با نام Correlation Matrix for Estimates of Fixed Effects که من بخش‌هایی از آن را آورده‌ام، ضریب همبستگی بین سطوح مختلف هر کدام از فاکتورهای اثر ثابت، در مقایسه با سطح رفرنس آمده است.

 

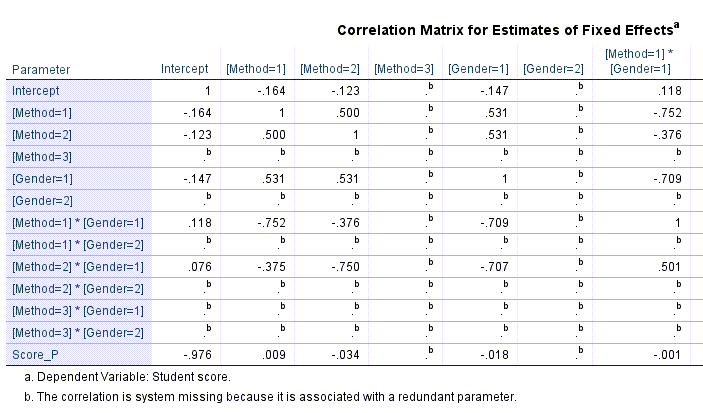
به عنوان مثال عدد 0.531 موجود در جدول بالا نشان می‌دهد، رابطه بین نمره دانش‌آموزان دختر با متد آموزشی A در مقایسه با دانش‌آموزان پسر یک رابطه مثبت و مستقیم و اندازه ضریب همبستگی (مجانبی) آن برابر با 0.531 است.

همچنین در ادامه می‌توانید جدول Covariance Matrix for Estimates of Fixed Effects را مشاهده کنید.

 

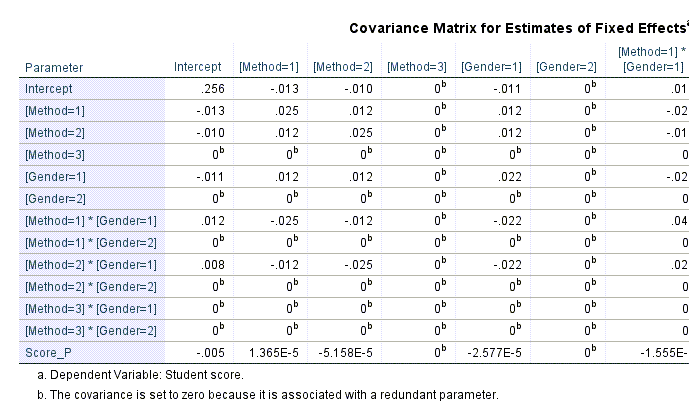
این جدول همانند جدول بالا است و از آنجا که ضریب همبستگی‌ها از روی کوواریانس ساخته می‌شوند، در اینجا ماتریس کوواریانس بین سطوح مختلف هر کدام از فاکتورهای اثر ثابت، در مقایسه با سطح رفرنس، آمده است.

خب حال بیایید به بررسی فاکتورهای با اثر تصادفی در این مثال بپردازیم. جدول زیر با نام Estimates of Covariance Parameters کوواریانس براورد شده اثرات تصادفی را نشان می‌دهد.

 

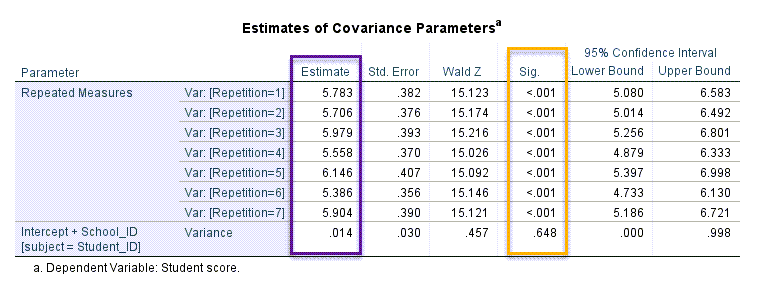
برای فهم بهتر این جدول لازم است یکبار دیگر مقاله اثرات تصادفی در آنالیز واریانس Random Effects ANOVA را مطالعه کنیم. من در آن مقاله بیان کردم که آزمون فرضیه‌ها در یک مدل اثرات تصادفی به صورت زیر خواهد بود.

$ \displaystyle {{H}_{0}}:\sigma _{\tau }^{2}=0\begin{array}{*{20}{c}} {} & {vs} & {} \end{array}{{H}_{1}}:\sigma _{\tau }^{2}>0$

در واقع وقتی مطالعه ما آنالیز از نوع اثرات تصادفی است، مقایسه میانگین‌ها دیگر مناسب نیست زیرا گروه‌ها به صورت تصادفی انتخاب می‌شوند و ما اصولاٌ از اثرات تصادفی استفاده می‌کنیم به دلیل اینکه قابل تعمیم به جمعیت بزرگتر خود هستند.

در یک مطالعه با اثر تصادفی به جای اینکه به نتایج هر گروه به تصادف انتخاب شده علاقمند باشیم (کاری که در یک مطالعه اثر ثابت انجام می‌دهیم) به بررسی اثر همه‌ی گروه‌ها علاقه‌مند هستیم. بنابراین آزمون فرضیه ما در یک طرح اثرات تصادفی، مقایسه میانگین بین گروه‌ها نیست. بلکه فرضیه صفر و جایگزین را به صورت بالا تعریف می‌کنیم.

در اینجا فرض صفر یعنی $ \displaystyle \sigma _{\tau }^{2}=0$ به معنای این است که پراکندگی و انحراف معیار، بین گروه‌های اثر تصادفی وجود ندارد. به بیان دیگر گروه‌ها مانند هم هستند و اثر معنادار بر کمیت وابسته Y ندارند.

از طرف دیگر فرض جایگزین یعنی $ \displaystyle \sigma _{\tau }^{2}>0$ به معنای این است که پراکندگی و انحراف معیار، بین گروه‌های اثر تصادفی وجود دارد و آن‌ها مشابه هم نیستند.

حال جدول بالا یعنی جدول کوواریانس براورد شده اثرات تصادفی نشان می‌دهد در همه‌ی تکرارها (شش بار آزمون تکرار شده بود)، فرض صفر به معنای برابر بودن واریانس نمرات، رد می‌شود و می‌پذیریم که در هر تکرار واریانس و پراکندگی نمرات دانش‌آموزان، معنادار است (P-value < 0.001). عدد و مقدار واریانس نیز برای هر تکرار در ستون Estimate آمده است.

نکته دیگری که از جدول بالا به دست می‌آید این است که فرضیه برابر بودن واریانس‌ها برای اثر تصادفی مولفه مدرسه (به خاطر داشته باشید ما به تصادف 17 مدرسه را انتخاب کرده بودیم) تایید می‌شود (P-value = 0.648). این مطلب نشان می‌دهد واریانس نمرات دانش‌آموزان از یک مدرسه به مدرسه دیگر با یکدیگر تفاوت معنادار ندارد. به این صورت که فاکتور مدرسه تاثیر معناداری بر نمرات دانش‌آموزان در آزمون‌ها ندارد.

در ادامه و خروجی‌های نرم‌افزار جدول Correlation Matrix for Estimates of Covariance Parameters دیده می‌شود.

 

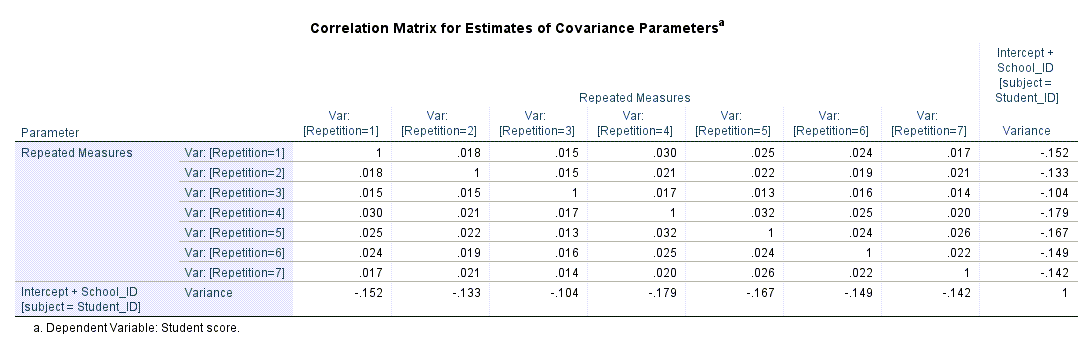
در این جدول ماتریس همبستگی بین براوردهای کوواریانس اثرات تصادفی، به دست آمده است. در واقع این جدول ضرایب همبستگی پارامترهای جدول بالاتر از خود یعنی جدول Estimates of Covariance Parameters را نشان می‌دهد. نتایج این جدول تاحدی بیانگر پایین بودن ضریب همبستگی بین پارامترهای براورد شده اثرات تصادفی با یکدیگر می‌باشد.

همچنین علاوه بر ماتریس همبستگی بالا، ماتریس کوواریانس بین براوردهای کوواریانس اثرات تصادفی نیز به دست آمده است.

 

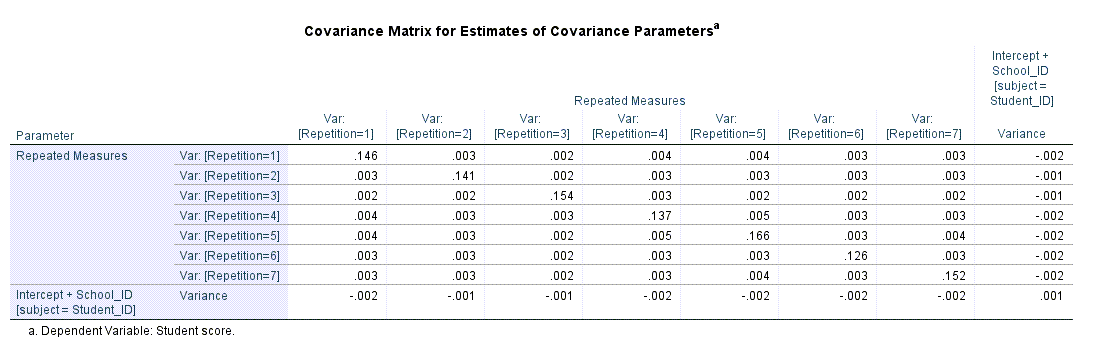
در ادامه نتایج جدول زیر با نام Random effect covariance (G) کوواریانس اثر تصادفی، دیده می‌شود. من در تصویر زیر بخشی از این جدول را آورده‌ام.

 

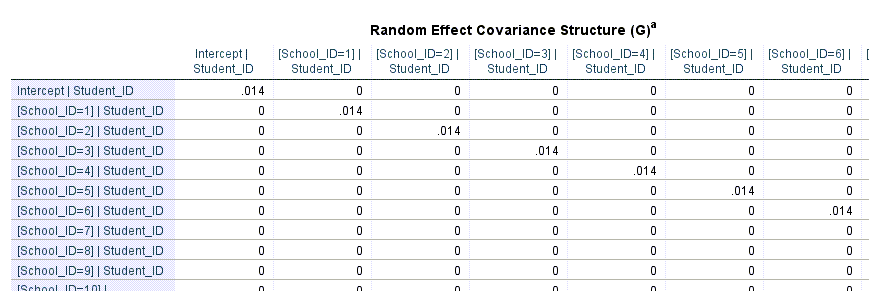
نتایج این جدول به انتخاب ما در تنظیمات نرم‌افزار و در پنجره Random Effects بخش Covariance Type، بستگی دارد. به خاطر داشته باشید ما در آن‌جا گزینه‌ی Scaled Identity را انتخاب کردیم. این گزینه‌ی دارای ساختار واریانس ثابت است. در این ساختار فرض بر این است که ارتباطی بین هیچ یک از فاکتورها وجود ندارد. این مطلب یعنی استقلال بین فاکتورها، توجیه می‌کند که چرا اعداد غیر از قطر در جدول بالا برابر با صفر به دست آمده‌اند.

این جدول نشان می‌دهد اثر تصادفی شماره شناسایی مدرسه واریانسی برابر با 0.014 دارد. خوب است به این نکته توجه کنید که ما در یک مدل آمیخته فرض می‌کنیم که اثر تصادفی درای توزیع احتمال نرمال با میانگین صفر و واریانس $\displaystyle \sigma _{\tau }^{2}$ است. در جدول بالا مقدار عددی $ \displaystyle \sigma _{\tau }^{2}$ را به دست آورده‌ایم.

نکته دیگر، از آن جا که شماره هر دانش‌آموز به عنوان Subject Variable وارد شده است، نتایج مبتنی بر شماره شناسایی هر دانش‌آموز به دست آمده است.

همچنین می‌توانیم جدول کوواریانس باقیمانده‌ها Residual Covariance (R) Matrix دیده می‌شود.

 

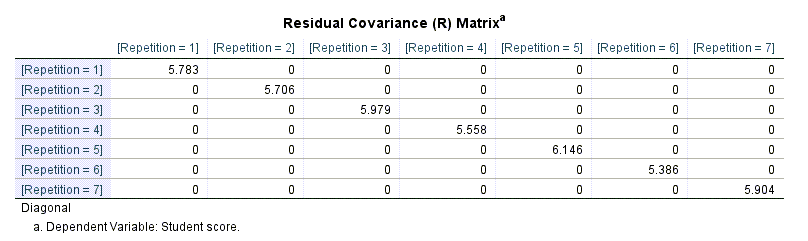
همان‌گونه که قبلاً بیان کردیم، در یک مدل آمیخته، تکرارها ساختار کوواریانس باقیمانده‌ها را مدل می‌کنند. در این جدول از آن‌جا که تکرارها مستقل از یکدیگر در نظر گرفته می‌شوند، بنابراین کوواریانس بین آن‌ها صفر است. در جدول بالا نیز مشاهده می‌کنید که آرایه‌های غیرقطر برابر با صفر به دست آمده‌اند.

آرایه‌های روی قطر، مقدار عددی کوواریانس باقیمانده‌های هر تکرار را نشان می‌دهند. هر چقدر این عدد بزرگتر باشد نشان می‌دهد، همبستگی بین نمرات دانش‌آموزان در آن تکرار بیشتر بوده است.

خروجی‌های بعدی که با نام میانگین‌های حاشیه‌ای براورد شده Estimated Marginal Means آمده‌اند، نتایج مفیدی هستند که به تفکیک به ازای هر کدام از فاکتورهای اثر ثابت متد آموزشی، جنسیت و اثر متقابل بین آن‌ها به دست آمده‌اند.

 

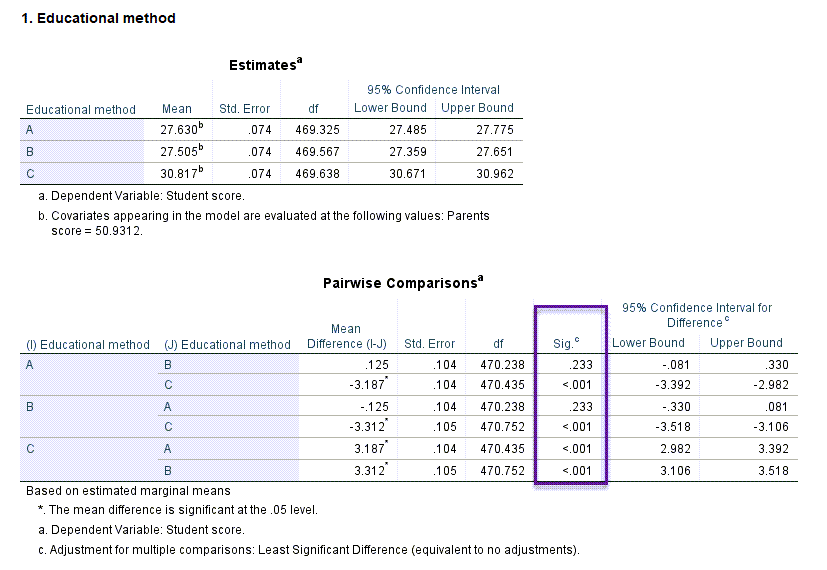
در این جدول میانگین‌های حاشیه‌ای براورد شده نمرات دانش‌آموزان همراه با فواصل اطمینان آن به ازای هر کدام از متدهای آموزشی به دست آمده است. همچنین در جدول بعدی با نام Pairwise Comparisons به مقایسه میانگین حاشیه‌ای نمرات دانش‌آموزان در هر متد آموزشی با متد دیگر پرداخته شده است.

نتایج به دست آمده در جدول بالا نشان می‌دهد میانگین نمرات در متد A و B با هم تفاوتی ندارند (P-value = 0.233). با این حال روش آموزشی C هم با A و هم با B متفاوت است (P-value < 0.001) و به صورت معنادار دارای میانگین نمرات بالاتری به دست آمده است.

همچنین در ادامه می‌توانید جدول میانگین‌های حاشیه‌ای براورد شده نمرات دانش‌آموزان به ازای دختر و پسر را مشاهده کنید.

 

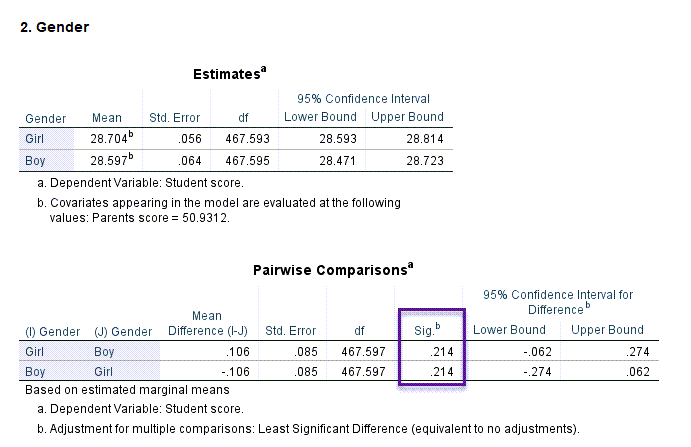
نتایج به دست آمده نشان می‌دهد دختران کمی بهتر از پسر و میانگین آن‌ها بالاتر بوده است، با این حال این نتیجه معنادار به دست نیامده است (P-value = 0.214).

در نهایت می‌توانید جدول میانگین‌های حاشیه‌ای اثرات متقابل متد آموزشی و جنسیت را مشاهده کنید.

 

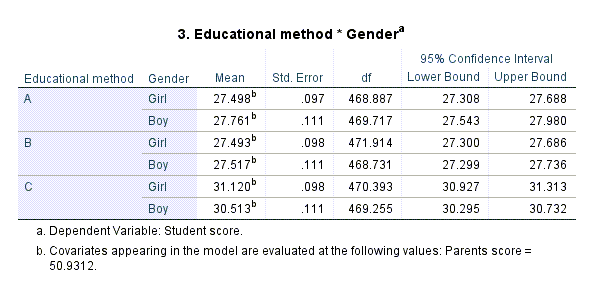
در این جدول میانگین نمرات دانش‌آموزان به ازای هر کدام از متد آموزشی به تفکیک دختر و پسر به دست آمده است. واضح است که این نتایج ناقص است و یک چیزی ندارد و آن جدول با نام Pairwise Comparisons است که به مقایسه میانگین حاشیه‌ای نمرات دانش‌آموزان در هر متد آموزشی و هر جنسیت با متد و جنسیت دیگر بپردازد. برای به دست آوردن این جدول لازم است در نرم‌افزار، برنامه Syntax نوشته شود. در این زمینه من در سایت گراف پد دو مقاله نوشته‌ام. علاقمند بودید در اینجا و اینجا آن‌ها را بخوانید. در این مقالات، من نحوه نوشتن Syntax در مطالعات دارای اثر متقابل جهت به دست آوردن جدول مقایسه‌های چندگانه را آورده‌ام.

به خاطر داشته باشید در تنظیمات تب از نرم‌افزار خواستیم مقادیر پیش‌بینی خود از کمیت وابسته یعنی نمره دانش‌آموز را بر مبنای مدل اثر ثابت (بدون اثرات تصادفی) و همچنین بر مبنای مدل آمیخته (شامل اثرات ثابت و تصادفی) به دست آورد. انتخاب این گزینه‌ها سبب می‌شود در فایل دیتا ستون‌های جدیدی ایجاد شود. در تصویر زیر آن‌ها را ببینید.

 

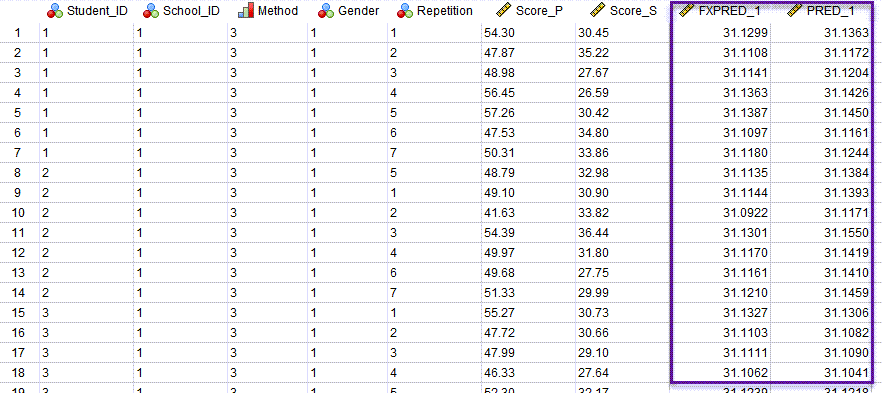
همان‌گونه که مشاهده می‌کنید در فایل دیتا یک ستون با نام Fixed Predicted Values و دیگری با نام Predicted Values اضافه شده است. این ستون‌ها بر مبنای مدل بر مبنای اثر ثابت (داده‌های ستون به نام FXPRED_1) و همچنین مدل بر مبنای آمیخته (داده‌های ستون PRED_1) به پیش‌بینی و براورد نمره هر دانش‌آموز در هر بار تکرار پرداخته است. همان‌گونه که می‌دانیم اختلاف عددی بین مقدار نمره واقعی مشاهده شده و مقدار پیش‌بینی شده توسط مدل ثابت یا آمیخته، تحت عنوان خطا یا Error شناخته می‌شود.

 

 

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2024). Mixed Model Analysis of Variance in SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/mixed-models-linear-spss/.php

For example, if you viewed this guide on 12^th January 2024, you would use the following reference

GraphPad Statistics (2024). Mixed Model Analysis of Variance in SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2024, from https://graphpad.ir/mixed-models-linear-spss/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.