اثرات تصادفی در آنالیز واریانس Random Effects ANOVA با نرم‌افزار SPSS

 Random-Effects 

سوال خوب است در ابتدا به یک سوال پاسخ دهیم. سوال این است که از کجا بدانیم اثرات و فاکتورهای اصلی مطالعه ما از نوع ثابت هستند یا تصادفی. در واقع آن‌ها Random Effect Factor هستند و یا Fix Effect Factor؟ کدامیک ثابت هستند و کدامیک تصادفی؟ یا به عبارت بهتر اثر ثابت و یا تصادفی چه تفاوتی با هم دارند؟

پاسخ به این سوال‌ها در این نکته نهفته شده است که گروه‌ها و سطوح مختلف فاکتورها چگونه انتخاب شده‌اند؟ آیا آن‌ها شامل یک مجموعه سطوح بزرگنری بوده‌اند و از درون یک مجموعه بزرگتر به تصادف انتخاب شده‌اند و یا اینکه از یک مجموعه بزرگتر نبوده‌اند و گروه‌های ثابتی هستند.

به عنوان یک مثال ساده، جنسیت که شامل دو گروه مردان و زنان است، در هر مطالعه‌ای به عنوان یک اثر ثابت یا Fix Factor در نظر گرفته می شود. ساده است به دلیل اینکه ما دو گونه جنسیت بیشنر نداریم. در واقع ما انواع مختلف جنسیت نداریم که بخواهیم برخی از این گونه‌ها را به تصادف انتخاب کنیم و گونه‌های انتخاب شده را در مطالعه قرار دهیم.

به عنوان مثال دیگر فرض کنید ما در یک مطالعه اقلیم شناسی بخواهیم، تاثیر سطوح و گونه‌های مختلف اقلیمی و سرزمینی کشور را بر روی بارش باران به عنوان کمیت وابسته به دست بیاوریم. از آن‌جا که ما گونه‌های مختلف اقلیمی و سرزمینی داریم، می‌توانیم برخی از آن‌ها را به تصادف انتخاب کنیم. در این حالت کمیت مستقلی که به عنوان فاکتور اقلیم شناخته می شود و شامل چندین گونه است، به دلیل اینکه از این گونه‌ها یک مجموعه بزرگتر گونه‌ها انتخاب شده‌اند، به عنوان فاکتور تصادفی یا Random Factor وارد مدل و نرم‌افزار می‌شوند.

 

مثال آنالیز واریانس با اثرات تصادفی

 Example 

فرض کنید در یک کارخانه که محصول خاصی را تولید می‌کند می‌خواهیم تاثیر اپراتور دستگاه بر روی کیفیت نهایی محصول به دست آمده را اندازه‌گیری کنیم. نکته‌ای که وجود دارد این است که از آن‌جا که ما با تعداد زیادی اپراتور روبه‌رو هستیم، بنابراین همه آن‌ها را نمی‌توانیم وارد مطالعه کنیم، بلکه می‌بایست یک نمونه تصادفی از این اپراتورها را انتخاب کنیم. در این حالت “اپراتور” به عنوان یک فاکتور با اثر تصادفی، در مطالعه قرار می‌گیرد.

در تصویر زیر می‌توانید بخشی از فایل دیتا این مثال را مشاهده کنید. از اینجا می‌توانید داده‌ها و نتایج این مثال را دریافت کنید.

 

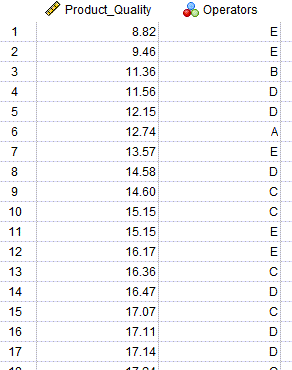
در این داده‌ها ستون با نام Product_Quality به عنوان کیفیت عددی محصول و ستون Operators به عنوان اپراتور دستگاه که در 5 گروه قرار گرفته‌‌اند، آمده است. همان‌گونه که بیان کردیم از آن‌جا که اپراتورهای دستگاه از جامعه بزرگتر همه‌ی اپراتورها انتخاب شده‌اند، بنابراین اپراتور به عنوان یک مولفه و اثر تصادفی بر کیفیت محصول در نظر گرفته می‌شود.

هدف ما در این مطالعه این است که دریابیم آیا نوع اپراتور دستگاه، بر کیفیت نهایی محصول اثرگزار است یا خیر. نکته مهمی که در اینجا وجود دارد و ما در مقاله اثرات ثابت یا تصادفی هم به آن پرداختیم، این است هنگامی که ما فاکتوری را به عنوان اثر تصادفی در نظر می‌گیریم، از آن‌جا که این فاکتور، نمونه تصادفی از یک کل است و از آن کل به تصادف انتخاب شده است، بنابراین نتایج به دست آمده بر مبنای این فاکتور را می‌توانیم به آن مجموعه بزرگتر تعمیم دهیم. در واقع Random Factor این قابلیت را دارد که به مجموعه بزرگتری که از آن می‌آید، گسترش یابد.

این مطلب در این مثال به معنای این است که ما نتایج به دست آمده از بررسی این 5 نوع اپراتور بررسی شده را می‌توانیم به همه‌ی اپراتورها تعمیم دهیم و بگوییم آیا نوع اپراتور بر کیفیت محصول اثر دارد یا اثری ندارد.

خوب است به این نکته هم اشاره کنیم که نام دقیق آنالیز این مثال آنالیز واریانس اثرات تصادفی یک طرفه One-way Random Effects Analysis of Variance است. یک طرفه به این دلیل که فقط یک کمیت مستقل Independent Variable (نوع اپراتور) در این مثال وجود دارد.

 

تئوری آنالیز واریانس با اثرات تصادفی

 Formulas 

یک طرح واریانس یک طرفه با اثرات تصادفی، به صورت زیر تعریف می‌شود.

$ \displaystyle {{y}_{{ij}}}=\mu +{{\tau }_{i}}+{{\varepsilon }_{{ij}}}\begin{array}{*{20}{c}} {} \end{array}\left\{ {\begin{array}{*{20}{c}} {i=1,2,….,k} \\ {j=1,2,….,n} \end{array}} \right\}$

در این طرح، $ \displaystyle {{y}_{{ij}}}$ به عنوان اندازه عددی کمیت وابسته برای i امین گروه تصادفی و j امین نفر، $ \displaystyle \mu $ اثر ثابت، $ \displaystyle {{\tau }_{i}}$ اثر i امین گروه در بین k گروه به تصادف انتخاب شده و $ \displaystyle {{\varepsilon }_{{ij}}}$ خطای مطالعه برای i امین گروه تصادفی و j امین نفر، می‌باشد.

از آنجا که در این طرح هم جمله خطا یعنی $ \displaystyle {{\varepsilon }_{{ij}}}$ و هم اثر $ \displaystyle {{\tau }_{i}}$ کمیت تصادفی (Random Variable) هستند، بنابراین می‌توانیم آن‌ها را به صورت توزیع احتمال نرمال زیر بنویسیم.

$ \displaystyle {{\varepsilon }_{{ij}}}\sim N(0,{{\sigma }^{2}})\begin{array}{*{20}{c}} {} & \And & {} \end{array}{{\tau }_{i}}\sim N(0,\sigma _{\tau }^{2})$

از آنجا که $ \displaystyle {{\tau }_{i}}$ و $\displaystyle {{\varepsilon }_{{ij}}}$ از یکدیگر مستقل هستند، بنابراین واریانس‌های $ \displaystyle {{\sigma }^{2}}$ و $ \displaystyle \sigma _{\tau }^{2}$ به عنوان مولفه‌های واریانس Variance Components نامیده می‌شوند. در این زمینه این مقاله را ببینید.

 نکته مهم 

ما معمولاً عادت کرده‌ایم هنگامی که آنالیز واریانس انجام دهیم به آزمون مقایسه میانگین در بین گروه‌های کمیت مستقل مطالعه خود بپردازیم. از آن‌جا که آنالیز واریانس را بیشتر در مدل‌های اثر ثابت دیده‌ایم، بنابراین این مقایسه صحیح و درست است. با این حال وقتی مطالعه ما آنالیز واریانس از نوع اثرات تصادفی است، مقایسه میانگین‌ها دیگر مناسب نیست زیرا گروه‌ها به صورت تصادفی انتخاب می‌شوند و ما اصولاٌ از اثرات تصادفی استفاده می‌کنیم به دلیل اینکه قابل تعمیم به جمعیت بزرگتر خود هستند.

در یک مطالعه با اثر تصادفی به جای اینکه به نتایج هر گروه به تصادف انتخاب شده علاقمند باشیم (کاری که در یک مطالعه اثر ثابت انجام می‌دهیم) به بررسی اثر همه‌ی گروه‌ها علاقه‌مند هستیم. بنابراین آزمون فرضیه ما در یک طرح اثرات تصادفی، مقایسه میانگین بین گروه‌ها نیست. بلکه فرضیه صفر و جایگزین را به صورت زیر تعریف می‌کنیم.

$ \displaystyle {{H}_{0}}:\sigma _{\tau }^{2}=0\begin{array}{*{20}{c}} {} & {vs} & {} \end{array}{{H}_{1}}:\sigma _{\tau }^{2}>0$

فرض صفر یعنی $ \displaystyle \sigma _{\tau }^{2}=0$ در اینجا به معنای این است که پراکندگی و انحراف معیار، بین گروه‌های اثر تصادفی وجود ندارد. به بیان دیگر گروه‌ها مانند هم هستند و اثر معنادار بر کمیت وابسته Y ندارند.

از طرف دیگر فرض جایگزین یعنی $ \displaystyle \sigma _{\tau }^{2}>0$ به معنای این است که پراکندگی و انحراف معیار، بین گروه‌های اثر تصادفی وجود دارد و آن‌ها مشابه هم نیستند.

 

حل مثال آنالیز واریانس با اثرات تصادفی

 Results 

حال بیایید به همان مثال بالا و بررسی اثر تصادفی اپراتور دستگاه بر روی کیفیت محصول بپردازیم. از مسیر زیر در نرم‌افزار SPSS جهت تحلیل آنالیز واریانس با اثر تصادفی، استفاده می‌کنیم.

 Analyze → General Linear model → Univariate  

در این صورت پنجره زیر با نام Univariate برای ما باز می‌شود.

 

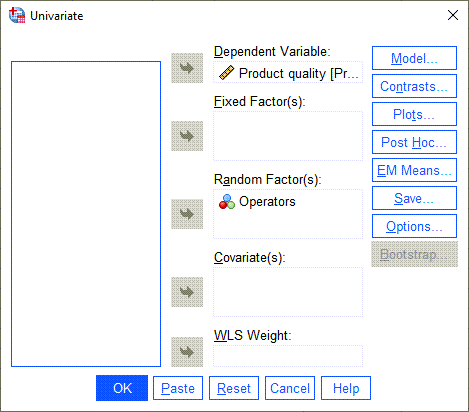
در کادر Dependent Variable که همان کمیت وابسته مطالعه است، کیفیت محصول و در کادر Random Factor(s) اپراتور دستگاه قرار می‌گیرد. با همین انتخاب انجام تحلیل واریانس با اثر تصادفی (Operators در کادر Random Factor قرار گرفته است)، قابل امکان است. با این حال چنانچه بخواهیم نتایج و خروجی‌های بیشتری نیز داشته باشیم، می‌توانیم تب‌ها و گزینه‌های دیگر نرم‌افزار را نیز مشاهده کنیم.

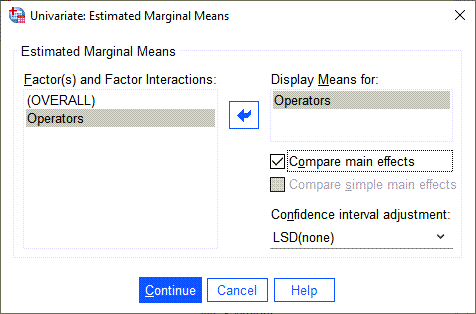
به عنوان مثال با استفاده از تب می‌توانیم به مقایسه هر کدام از اپراتورهای دستگاه با یکدیگر بپردازیم. در تصویر زیر پنجره و تنظیمات آن را می‌بینید.

 

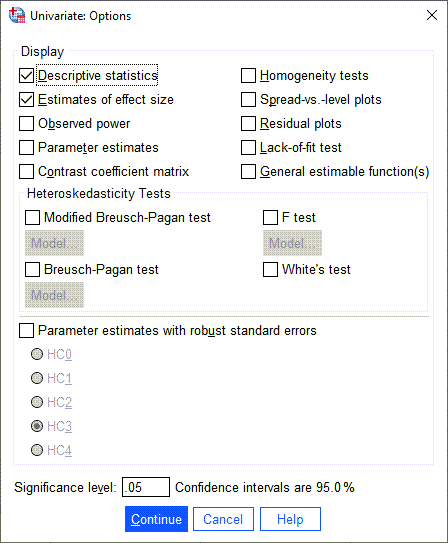
همچنین در تب می‌توانیم گزینه‌ها و امکانات بیشتری جهت مشاهده نتایج به دست آوریم. یافته‌هایی مانند آماره‌های توصیفی، براورد اندازه اثر، آزمون همگنی واریانس و یا آزمون‌های ناهمواریانسی (در این زمینه علاقمند بودید این لینک را ببینید) در این تب قرار دارند. من برای این مثال برخی از گزینه‌ها را انتخاب کرده‌ام.

 

در تب می‌توانیم به رسم نمودار کیفیت محصول به ازای هر کدام از اپراتورهای دستگاه بپردازیم. تصویر پنجره این تب را مشاهده می‌کنید.

 

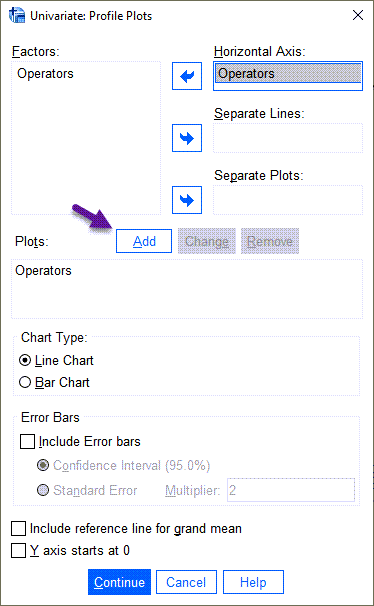
در پنجره تنظیمات Plots لازم است گزینه Add را بزنیم. در این پنجره نرم‌افزار SPSS انتخابی جهت رسم نمودار خطی و یا میله‌ای برای ما قرار داده است.

حال OK کنید. در این صورت می‌توانید نتایج و خروجی‌های نرم‌افزار SPSS در آنالیز واریانس اثرات تصادفی را مشاهده کنید.

در ابتدا جدول زیر با نام Descriptive Statistics مشاهده می‌شود.

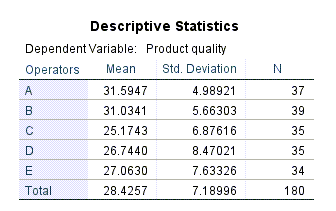
در این جدول می‌توانید آماره‌های توصیفی شامل میانگین، انحراف معیار و تعداد نمونه به ازای هر کدام از 5 اپراتور به تصادف انتخاب شده را مشاهده کنید.

جدول دیگر با نام Tests of Between-Subjects Effects مهمترین نتیجه در این آنالیز است. در تصویر زیر آن را می‌بینید.

 

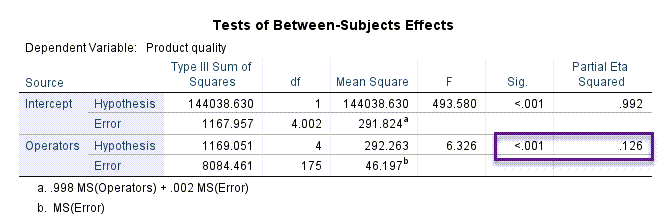
در این جدول به بررسی آزمون فرضیه زیر پرداخته شده است.

$ \displaystyle {{H}_{0}}:\sigma _{\tau }^{2}=0\begin{array}{*{20}{c}} {} & {vs} & {} \end{array}{{H}_{1}}:\sigma _{\tau }^{2}>0$

نتیجه به دست آمده بیانگر رد فرض صفر در سطح معنی‌داری $ \displaystyle \left( {\alpha =0.05} \right)$ است. این نتیجه نشان می‌دهد پراکندگی و واریانس کیفیت محصول در بین اپراتورهای دستگاه (این اپراتورها به تصادف انتخاب شده‌اند) با یکدیگر متفاوت است. این مطلب بیانگر تاثیرگزاری معنادار نوع اپراتور بر کیفیت محصول می‌باشد $ \displaystyle \left( {P-value<0.001,{{\eta }^{2}}=0.126} \right)$.

نکته دیگری که در این جدول وجود دارد، وجود دو منبع برای Error است. شاید برای شما سوال پیش بیاید که چرا ما با دو خط برای Error مواجه هستیم. در واقع به خاطر داشته باشید در یک مطالعه آنالیز واریانس با اثرات ثابت، فقط یک منبع برای Error نمایش داده می‌شود.

پاسخ سوال این است که ما در یک مدل اثرات تصادفی با دو خطا روبه‌رو هستیم. یک خطا، خطای اندازه‌گیری و براورد است که در همه‌ی مدل‌های انالیز واریانس و یا کوواریانس (و در حالت کلی‌تر همه‌ی مدل‌های خطی) وجود دارد. ما به این خطا خطای تصادفی و یا Random Error می‌گوییم. این همان خطایی است که با نام Error در منبع مربوط به اثرات تصادفی (در این مثال به نام Operators) دیده می‌شود و عدد مجموع مربعات SS آن برابر با 8084.46 شده است. به این نکته دقت کنید که اگر ما مدل اثرات تصادفی را به صورت یک مدل اثرات ثابت می‌شویم، باز هم همین مقدار عددی SS خطا را برای Error در مدل اثرات ثابت مشاهده می‌کردیم.

خطای دیگر در یک مدل اثرات تصادفی به خطای انتخاب تصادفی گروه‌های Random Factor از جامعه‌ی بزرگتر خود مربوط می‌شود. به یاد بیاورید که گفتیم در یک مدل اثرات تصادفی، گروه‌های Independent Variable به صورت تصادفی از یک مجموعه بزرگتر انتخاب می‌شوند. در جدول بالا این خطا با نام Error در زیر منبع Intercept نوشته شده است. مقدار عددی مجموع مربعات SS برای این خطا برابر با 1167.96 به دست آمده است.

در اینجا جدول دیگری با نام Expected Mean Squares وجود دارد. در تصویر زیر آن را می‌بینید.

 

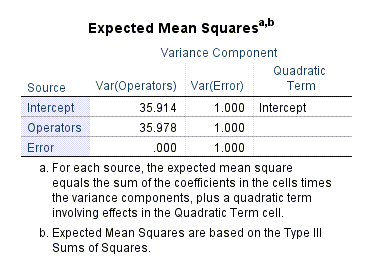
از میانگین مربعات مورد انتظار Expected Mean Square (EMS) به منظور براورد آماره F (و در نتیجه یافتن مقدار احتمال جهت تعیین معنادار بودن یا نبودن فاکتور مورد بررسی) استفاده می‌شود. در این موضوع و نحوه‌ی محاسبه آماره‌های این جدول علاقمند بودید می‌توانید این لینک و این لینک را ببینید.

از دیگر جدول‌ها و نتایج مفید در این مثال جدول Pairwise Comparisons می‌باشد. آن را ببینید.

 

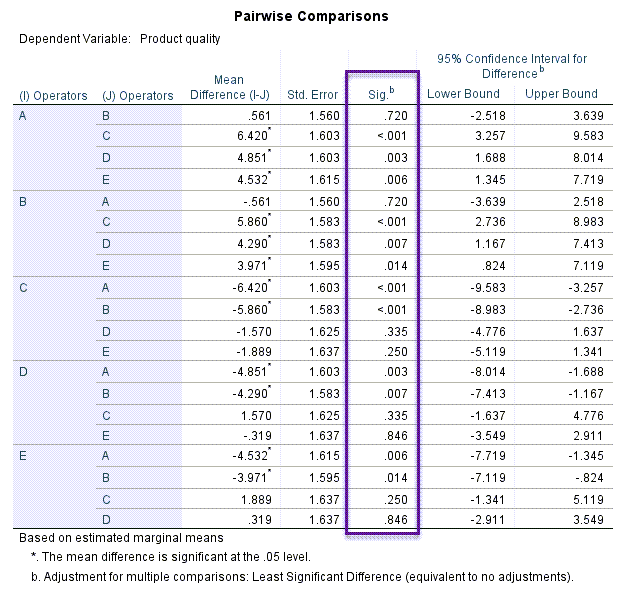
در این جدول به مقایسه کیفیت محصول در بین هر کدام از اپراتورها با اپراتور دیگر پرداخته شده است. به عنوان مثال این جدول نشان می‌دهد کیفیت محصول اپراتور نوع A از همه‌ی اپراتورها (به جز B) به صورت معنادار بیشتر است. کیفیت محصول اپراتور A از B نیز بیشتر است، منتهی این بیشتر بودن معنادار به دست نیامده است $ \displaystyle \left( {P-value=0.720} \right)$. بقیه‌ی نتایج را نیز می‌توانید در جدول بالا مشاهده کنید.

همچنین در پلات زیر می‌توانید نمودار کیفیت محصول به ازای هر کدام از اپراتورهای انتخاب شده را مشاهده کنید.

 

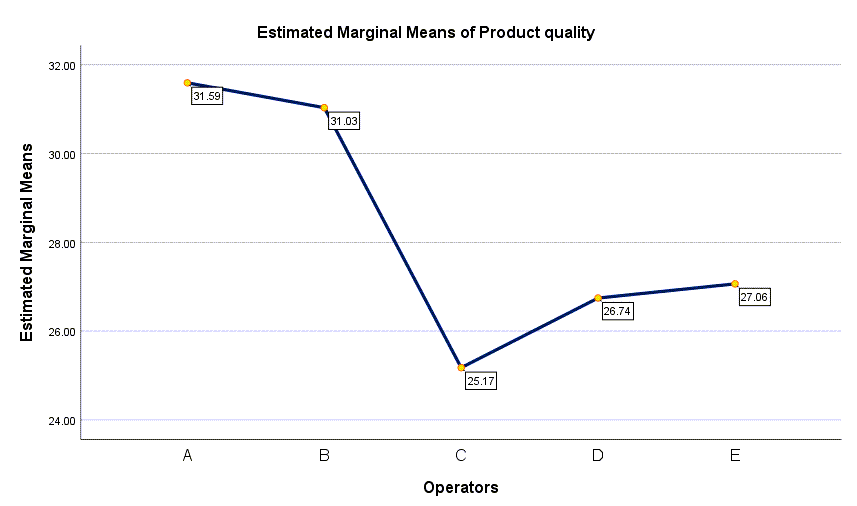
همان‌گونه که در این نمودار مشاهده می‌کنید، بیشترین کیفیت محصول مربوط به اپراتور A با عدد میانگین 31.59 و کمترین کیفیت محصول به اپراتور C با عدد میانگین 25.17 اختصاص دارد.

 

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2024). Random Effects ANOVA with SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/random-effects-anova-spss/.php

For example, if you viewed this guide on 12^th January 2024, you would use the following reference

GraphPad Statistics (2024). Random Effects ANOVA with SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2024, from https://graphpad.ir/random-effects-anova-spss/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.