مقایسه میانگین در طرح دو نمونه وابسته Paired-Samples T Test

توضیحات مقایسه میانگین در طرح دو نمونه وابسته برگرفته شده از کتاب روش های پیشرفته آماری و کاربردهای آن

دریافت ویدئو آموزش آزمون‌های مقایسه میانگین با SPSS

شامل 80 دقیقه ویدئو، 105 اسلاید، فایل‌های دیتا و نتایج نرم‌افزار SPSS

 

آنچه در مقاله قبلی به آن پرداختیم بررسی یک صفت در دو جامعه مستقل از یکدیگر بود، (مقایسه میانگین در طرح دو نمونه مستقل Independent-Samples T Test) با این حال بسیار اتفاق می‌افتد که بخواهیم دو صفت را در یک جامعه مورد بررسی قرار دهیم و یا این‌که بخواهیم یک صفت را در یک جامعه و در دو حالت قبل و بعد از یک رویداد بررسی کنیم.

من در این مقاله به دنبال این هستم که به مقایسه میانگین نمونه در دو گروه وابسته به یکدیگر بپردازم. به این مطالعه Paired-Samples T Test گفته می‌شود. این کار را با استفاده از نرم‌افزار SPSS انجام خواهیم داد. فایل دیتا این مقاله را می‌توانید از اینجا دریافت کنید.

در تصویر زیر بخشی از فایل دیتا را مشاهده می‌کنید. در این فایل به بررسی چند شاخص قلبی و عروقی مانند crp ،chol و sbp بر روی وزن افراد می‌پردازیم. 150 نفر مرد و زن که میزان فعالیت بدنی و همچنین وزن قبل و بعد آن‌ها پس از یک مداخله ورزشی به دست آمده، در این مثال گزارش شده است.

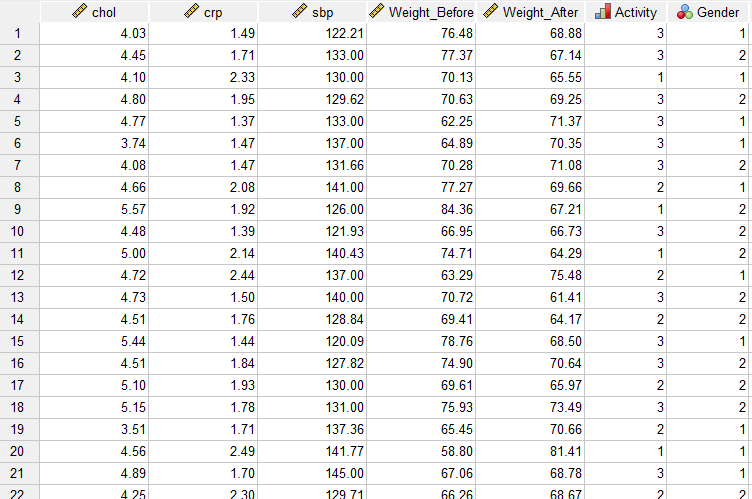
به عنوان یک مثال دیگر فرض کنید محقق می‌خواهد میانگین وزن قبل و بعد از مداخله ورزشی افراد را با یکدیگر مقایسه کند. او می‌خواهد فرضیه زیر را آزمون کند.

$ \displaystyle {{H}_{0}}:{{\mu }_{{\left( {Before,Weight} \right)}}}={{\mu }_{{\left( {After,Weight} \right)}}}\begin{array}{*{20}{c}} {} & {vs} & {} \end{array}{{H}_{1}}:{{\mu }_{{\left( {Before,Weight} \right)}}}\ne {{\mu }_{{\left( {After,Weight} \right)}}}$

ما می‌خواهیم علاوه بر آزمون فرضیه بالا، اندازه اثر اختلاف میانگین وزن قبل و بعد از مداخله را نیز محاسبه کنیم.

یکی از پیش‌فرض‌های انجام تحلیل پارامتری Paired-Samples T Test نرمال بودن داده‌ها در هر کدام از وزن‌های قبل و بعد از مداخله است. بنابراین ابتدا باید آزمون نرمالیتی انجام شود. در زمینه آزمون‌های نرمال، علاقمند بودید این لینک‌ها را ببینید. آزمون نرمال با استفاده از نرم‌افزار گراف پد و چگونه داده‌ها را به توزیع نرمال تبدیل کنیم؟

برای انجام آزمون نرمالیتی از مسیر زیر در نرم‌افزار SPSS استفاده می‌کنیم.

Analyze → Nonparametric Tests → Legacy Dialogs → 1-Sample K-S 

پنجره زیر با نام One-Sample Kolmogorov-Smirnov Test برای ما باز می‌شود.

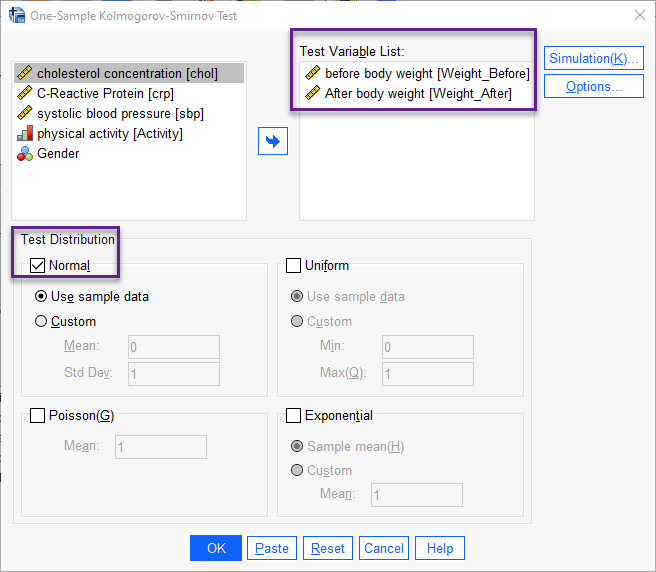
در کادر Test Variable List وزن‌های قبل و بعد از مداخله را قرار می‌دهیم. در بخش Test Distribution نیز گزینه Normal را انتخاب می‌کنیم. با OK کردن، جدول نتایج آزمون نرمالیتی در پنجره Output نرم‌افزار SPSS قابل مشاهده است.

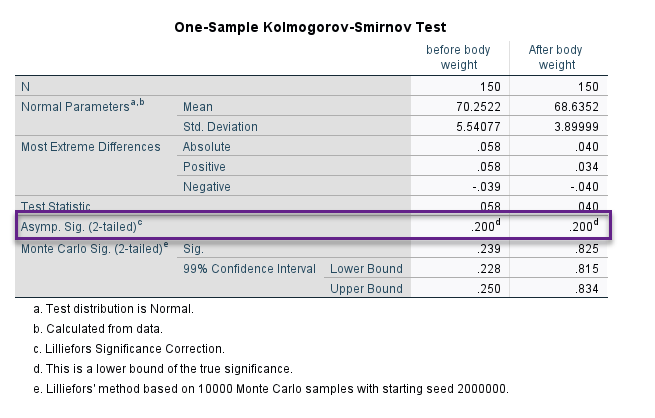
نتیجه به دست آمده در جدول One-Sample Kolmogorov-Smirnov Test بالا، بیانگر نرمال بودن داده‌های وزن هم قبل و هم بعد از مداخله است. بنابراین می‌توانیم از آزمون پارامتری Paired-Samples T Test استفاده کنیم.

برای انجام این آزمون از مسیر زیر در نرم‌افزار SPSS استفاده می‌کنیم.

Analyze → Compare Means → Paired-Samples T Test 

در این مسیر، پنجره زیر با نام Paired-Samples T Test برای ما باز می‌شود.

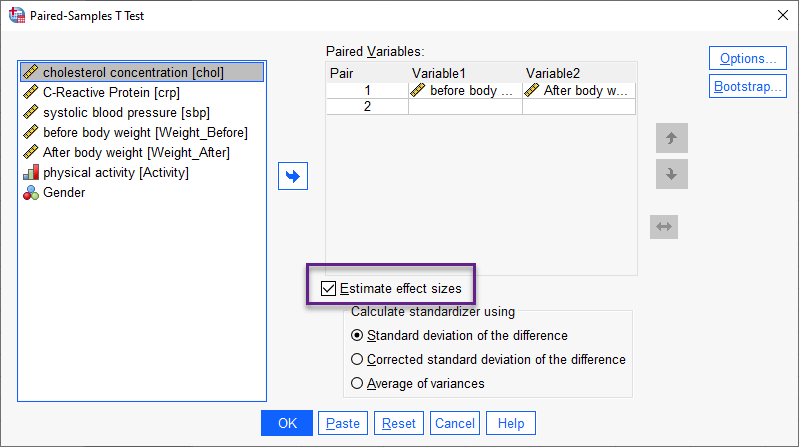
در کادر Paired Variables کمیت‌های وزن قبل و بعد از مداخله را قرار می‌دهیم. از آنجا که می‌خواهیم اندازه اثر را نیز محاسبه کنیم، گزینه Estimate effect sizes را انتخاب می‌کنیم. با OK کردن در پنجره و محیط Output نرم‌افزار SPSS نتایج و جداول زیر به دست می‌آید. درباره‌ی آن‌ها توضیح می‌دهیم.

در ابتدای نتایج جدول Paired-Samples Statistics دیده می‌شود. در این جدول آماره‌های توصیفی شامل تعداد نمونه، میانگین، انحراف معیار و انحراف معیار از میانگین برای وزن قبل و بعد از مداخله افراد به دست آمده است. این جدول نشان می‌دهد میانگین وزن قبل و بعد به ترتیب برابر با 70.25 و 68.63 کیلوگرم شده است.

در خروجی نتایج جدول دیگری با نام Paired Samples Test دیده می‌شود.

در این جدول نتایج آزمون فرضیه بالا یعنی مقایسه میانگین وزن قبل و بعد افراد به دست آمده است. نتیجه به دست آمده نشان می دهد میانگین وزن قبل و بعد از مداخله با یکدیگر اختلاف معنادار دارند (P-value = 0.004).

اندازه اثر اختلاف قبل و بعد نیز که ما در این متن به دنبال آن بودیم در جدول زیر با نام Paired Samples Effect Sizes این یافته به دست آمده است.

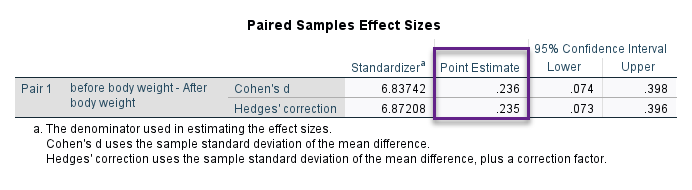
اندازه اثر بر مبنای روش‌های Cohen’s d و Hedges’ correction به دست آمده است. عدد براورد شده برای اندازه اثر اختلاف بین میانگین وزن قبل و بعد از مداخله افراد برابر با 0.236 و 0.235 است. این Effect Size بیانگر وجود اندازه اثر تقریباً ضعیف و تاحدی متوسط اختلاف بین وزن قبل و بعد است.

در جدول Paired Samples Effect Sizes، فواصل اطمینان 95 درصد برای اندازه اثر نیز به دست آمده است. به عنوان مثال فاصله اطمینان 95 درصد برای d کوهن برابر با (0.398 ,0.074) گزارش می‌شود. چنانچه به توضیحات بیشتری در زمینه اندازه اثر و Effect Size علاقمند هستید، این لینک را در سایت گراف پد ببینید. (اندازه اثر در آزمون‌های مقایسه میانگین)

Effect Size می‌تواند عددی مثبت و یا منفی باشد. من در عبارات زیر محدوده‌های مختلف عدد براورد شده برای قدرمطلق Effect Size را بیان کرده‌ام.

•     اندازه اثر 0.2 = d و کمتر را یک اندازه اثر کوچک و غیرمعنادار بیان می‌کنیم.
•     اندازه اثر d بین 0.2 و 0.5  را اندازه اثر متوسط گزارش می‌کنیم.
•     اندازه اثر d بین 0.5 و 0.8  اندازه اثر بزرگ و قوی بیان می‌شود
•     اندازه اثر d > 0.8 نیز به عنوان یک اندازه اثر بسیار قوی گزارش می‌شود.