آزمون ناپارامتری من ویتنی Mann-Whitnety U Test با نرم افزار SPSS

 Mann-Whitney 

دریافت مجموعه آموزش آزمون‌های ناپارامتری

شامل 350 دقیقه ویدئو، فایل دیتا و نتایج SPSS

برخلاف آزمون Independent-Samples T، آزمون من ویتنی به شما امکان می‌دهد بسته به فرضیاتی که در مورد توزیع داده‌های خود می‌کنید، نتایج متفاوتی بگیرید. این نتیجه‌گیری‌ها می‌تواند از بیان ساده این که آیا این دو جمعیت با یکدیگر تفاوت دارند تا تعیین اینکه آیا میانه گروه‌ها با یکدیگر تفاوت دارد، قرار بگیرد. این نتیجه‌گیری‌های متفاوت به شکل توزیع داده‌های شما بستگی دارد که در ادامه درباره‌ی آن توضیح خواهیم داد.

انجام هر آزمون و تحلیل آماری نیاز به برقراری تعدادی پیش فرض و چارچوب‌های آنالیز دارد. بنابراین در ابتدا مناسب است درباره‌ی این موضوع صحبت کنیم.

پیش فرض‌های آزمون من ویتنی

 Assumptions 

قبل از اینکه بخواهیم درباره‌ی نحوه انجام آزمون من ویتنی در نرم‌افزار SPSS صحبت کنیم، پیش فرض‌های مختلفی را توضیح می‌دهیم که لازم است داده‌های شما با آن‌ها مطابقت داشته باشند تا آزمایش Mann-Whitney U نتیجه معتبری به شما بدهد. این پیش فرض‌ها به صورت زیر هستند.

کمیت وابسته شما باید در مقیاس ترتیبی یا پیوسته اندازه‌گیری شود. نمونه‌هایی از کمیت‌های ترتیبی شامل طیف لیکرت (مثلاً مقیاس 5 گزینه‌ای از کاملاً موافقم تا کاملاً مخالفم). نمونه‌هایی از کمیت‌های پیوسته عبارتند از زمان (اندازه‌گیری شده بر حسب ساعت)، هوش (اندازه‌گیری شده با استفاده از نمره IQ)، عملکرد در یک آزمون (از 0 تا 100)، وزن (بر حسب کیلوگرم).

کمیت مستقل شما باید از دو گروه طبقه‌بندی شده و مستقل تشکیل شده باشد. نمونه کمیت‌های مستقلی که این معیار را برآورده می‌کنند شامل جنسیت (مرد یا زن)، وضعیت اشتغال (شاغل یا بیکار)، فرد سیگاری (بله یا خیر) است.

مشاهدات باید از یکدیگر مستقل باشند، به این معنی که هیچ رابطه‌ای بین مشاهدات در هر گروه یا بین خود گروه‌ها وجود نداشته باشد. برای مثال، باید در هر گروه شرکت‌کنندگان متفاوتی وجود داشته باشد و هیچ شرکت‌کننده‌ای در بیش از یک گروه نباشد. این پیش فرض بیشتر یک موضوع طراحی مطالعه است تا چیزی که بتوانید آن را آزمایش کنید.

هنگامی که کمیت وابسته شما در هر دو گروه مستقل، فاقد توزیع نرمال هستند، می‌توان از آزمون Mann-Whitney استفاده کرد. با این حال، برای اینکه بدانید چگونه نتایج آزمون Mann-Whitney را تفسیر کنید، باید تعیین کنید که آیا دو توزیع شما (یعنی توزیع نمرات برای هر دو گروه کمیت مستقل) شکل یکسانی دارند یا خیر. برای درک بهتر به نمودار زیر نگاه کنید.

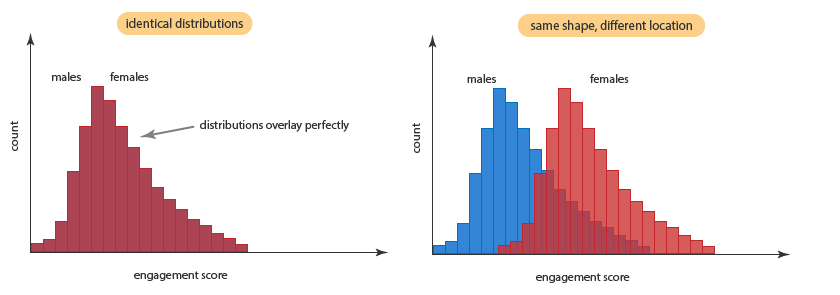
در دو نمودار بالا، توزیع نمرات برای مرد و زن شکل یکسانی دارد. در نمودار سمت چپ، نمی‌توانید توزیع نمرات را برای مردان و یا زنان به صورت جداگانه ببینید، به دلیل اینکه کاملاً بر یکدیگر منطبق هستند. با این حال، در نمودار سمت راست، حتی اگر هر دو توزیع، یک شکل دارند، با این حال مکان متفاوتی دارند. به این معنا که توزیع یکی از گروه‌های کمیت مستقل دارای مقادیر بالاتر یا کمتری نسبت به توزیع دیگر است. در مثال ما زنان دارای اعداد بالاتری نسبت به مردان هستند.

وقتی داده‌های خود را تحلیل می‌کنید، بسیار بعید است که دو توزیع یکسان باشند، اما ممکن است شکل مشابه داشته باشند. اگر شکل مشابهی دارند، می‌توانید از آزمون Mann-Whitney جهت مقایسه میانه‌های کمیت وابسته در دو گروه استفاده کنید. با این حال، اگر دو توزیع شکل متفاوتی دارند، فقط می‌توانید از آزمون من ویتنی برای مقایسه میانگین رتبه‌ها Mean Rank استفاده کنید.

مثال آزمون من ویتنی

 Example 

غلظت کلسترول در خون با خطر ابتلا به بیماری قلبی مرتبط است، به طوری که غلظت بالاتر کلسترول، نشان‌دهنده سطح بالاتر خطر و غلظت کمتر، بیانگر سطح خطر کمتر است. هم ورزش و هم کاهش وزن می‌توانند غلظت کلسترول را کاهش دهند. با این حال، مشخص نیست که آیا ورزش یا کاهش وزن برای کاهش غلظت کلسترول بهترین انتخاب است. بنابراین، یک محقق تصمیم گرفت بررسی کند که آیا ورزش یا مداخله کاهش وزن در کاهش سطح کلسترول مؤثر است یا خیر. برای این منظور، محقق نمونه‌ای تصادفی از مردان غیرفعال را که دارای اضافه ورن بودند، انتخاب کرد. سپس این نمونه به طور تصادفی به دو گروه تقسیم شد. گروه الف تحت یک رژیم غذایی کنترل شده با کالری (گروه “رژیم غذایی”) و گروه ب یک برنامه تمرینی (گروه “ورزش”) را انجام دادند. به منظور تعیین اینکه کدام برنامه درمانی موثرتر است، غلظت کلسترول بین دو گروه در پایان برنامه‌های درمانی مقایسه شد.

در تصویر زیر می‌توانید بخشی از داده‌ها را مشاهده کنید. فایل این مثال را از اینجا Mann-Whitnety U Test دریافت کنید.

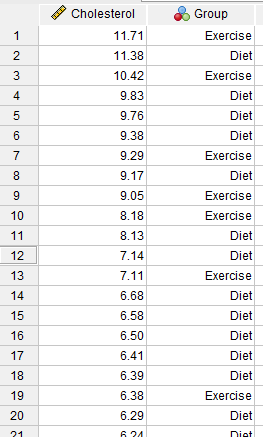
در داده‌های بالا غلظت کلسترول کمیت وابسته است که با نام Cholesterol آمده است. داده‌های کمیت مستقل نیز که به صورت گروه‌های رژیم غذایی Diet و ورزش Exercise قرار گرفته، در ستون با نام Group آمده است. از آنجایی که کمیت مستقل ما دو گروه داشت – “رژیم غذایی” و “ورزش” – به گروه رژیم غذایی مقدار 1 و به گروه ورزش مقدار 2 دادیم. اگر دو گروه خود را برچسب گزاری نکنید، نرم افزار SPSS نمی‌تواند بین آنها تمایز قائل شود و آزمون Mann-Whitney U اجرا نمی‌شود.

خب حال موضوعی که وجود دارد و من در پیش فرض شماره (4) بالا به آن پرداختم، به دست آوردن شکل توزیع داده‌ها در بین گروه‌های کمیت مستقل است. این کار به من کمک می‌کند تا بدانم چه نتیجه‌ای از آزمون من ویتنی برایم به دست می‌آید و تفسیر نتایج آن چیست.

برای انجام این کار کافی است، هیستوگرام داده‌ها را رسم کنید. در لینک (رسم هیستوگرام Histogram با نرم‌افزار SPSS) می‌توانید آموزش رسم هیستوگرام را مشاهده کنید.

من در شکل زیر نمودار فراوانی داده‌های غلظت به ازای هر کدام از گروه‌های ورزش و رژیم غذایی را رسم کرده‌ام. آن را ببینید.

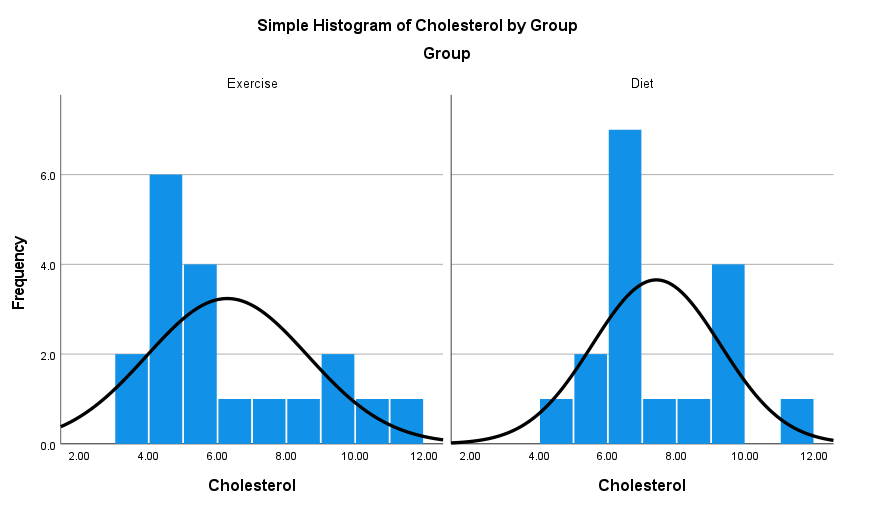
آنچه که از گراف بالا به دست می‌آید این است که به نظر نمی‌رسد، توزیع داده‌های غلظت در بین هر دو گروه مشابه با هم است و شکل هیستوگرام آن‌‌ها تا حدی مشابه با هم است. بنابراین می‌توانیم بگوییم که از آزمون Mann-Whitney جهت مقایسه میانگین‌های رتبه‌ای غلظت در دو گروه استفاده می‌کنیم.

یک نکته دیگری نیز که خوب است به آن بپردازیم این است که داده‌های غلظت در دو گروه رژیم غذایی و ورزش فاقد توزیع نرمال است $\displaystyle \left( {P-valu{{e}_{{Exercise}}}=0.001,\begin{array}{*{20}{c}} {} & {P-valu{{e}_{{Diet}}}=0.009} \end{array}} \right)$. چنانچه علاقمند هستید با استفاده از لینک (آزمون نرمال بودن داده ها Normality Test در نرم افزار SPSS) می‌توانید فرضیه نرمال بودن داده‌ها را آزمون کنید.

جهت انجام تحلیل ناپارامتری من ویتنی دو مسیر و رویه جداگانه در نرم‌افزار SPSS وجود دارد. من در ادامه هر یک را توضیح می‌دهم.

 Analyze → Nonparametric Tests → Legacy Dialogs → 2 Independent Samples 

با استفاده از مسیر بالا، پنجره زیر با نام Two-Independent-Samples Tests برای ما باز می‌شود.

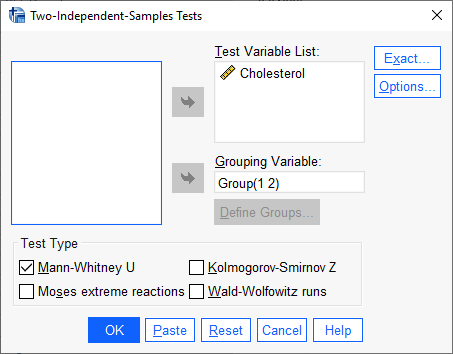
در این پنجره که مربوط به تنظیمات آزمون‌های ناپارامتری دو نمونه مستقل در نرم‌افزار SPSS است، داده‌‌‌های Cholesterol در کادر Test Variable List قرار می‌گیرد. همچنین ستون Group که در آن رژیم غذایی و یا ورزش را برای هر فرد مشخص کردیم، در بخش Grouping Variable قرار می‌گیرد. در اینجا لازم است با استفاده از دکمه به نرم‌افزار کدهای 1 و 2 که با استفاده از آن رژیم غذایی و یا ورزش را تعریف کردیم، معرفی کنیم.

چنانچه علاقمند باشیم برخی از آماره‌های توصیفی نیز برای ما ارایه شود، می‌توانیم از دکمه وارد پنجره زیر شویم و گزینه‌های Descriptive و Quartiles را انتخاب کنیم.

خب، حال OK‌ کنید و در ادامه نتایج و خروجی‌های نرم‌افزار SPSS که با استفاده از مسیر بالا به انجام آزمون من ویتنی پرداختیم را مشاهده کنید.

نتایج آزمون من ویتنی

 Results 

در پنجره Output می‌توانید خروجی‌های به دست آمده از آزمون ناپارامتری Mann-Whitney U را ببینید.

در ابتدای نتایج، جدول Descriptive Statistics آمده است. در تصویر زیر آن را می‌بینید.

آماره‌های توصیفی این جدول بدون در نظر گرفتن گروه‌های رژیم غذایی و ورزش، بر روی همه داده‌ها (36 مورد) به دست آمده است. نتایج مربوط به Group آن نیز قابل اعتنا نیست و به نظرم از ایرادات نرم‌افزار SPSS است که برای یک Variable از نوع گروه‌بندی شده Nominal آماره‌های توصیفی ارایه می‌دهد. صرفاً در جدول Descriptive Statistics بالا نتایج مربوط به سطر Cholesterol برای ما معتبر است.

جدول بعدی در خروجی‌های نرم‌افزار، با نام Ranks Table قرار دارد. در تصویر زیر آن را ببینید.

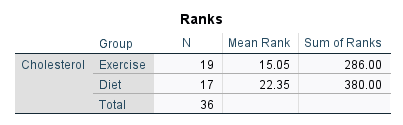
جدول بالا که از آن با نام جدول رتبه‌ها Ranks Table یاد می‌شود، خروجی آزمون Mann-Whitney U را ارایه می‌دهد. میانگین رتبه Mean Ranks و مجموع رتبه‌ها Sum of Ranks را برای دو گروه مورد آزمایش (گروه‌های ورزش و رژیم غذایی) نشان می‌دهد.

شاید برای شما این سوال پیش بیاید که منظور از رتبه‌ها و میانگین و مجموع آن‌ها چیست؟

من پاسخ به این سوال را به صورت کامل در کتاب روش‌‌های پیشرفته آماری و کاربردهای آن داده‌ام. علاقمند بودید به فصل دهم این کتاب مراجعه کنید.

جدول بالا بسیار مفید است زیرا نشان می‌دهد که کدام گروه را می‌توان دارای غلظت کلسترول بالاتری در نظر گرفت، این همان گروهی است که بالاترین میانگین رتبه را دارد. در این مثال، گروه رژیم غذایی بالاترین غلظت کلسترول را داشته است.

در نهایت در خروجی‌های نرم‌افزار جدول دیگری با نام Test Statistics دیده می‌شود.

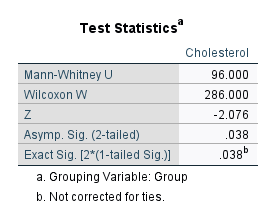
در این جدول می‌توانیم به فرضیه برابر بودن غلظت کلسترول در افراد دارای رژیم غذایی و یا ورزش پاسخ دهیم. قبلاً و بر مبنای عدم مشابه بودن توزیع غلظت در دو گروه نشان دادیم که آزمون من ویتنی می‌تواند فرضیه برابر بودن میانگین‌های رتبه‌ای را تست کند.

نتیجه جدول بالا نشان‌دهنده وجود اختلاف معنادار در میانگین رتبه‌ای غلظت کلسترول بین افراد رژیم غذایی و ورزش است $ \displaystyle \left( {U=96.00,\begin{array}{*{20}{c}} {} & {P-value=0.038} \end{array}} \right)$. به این ترتیب نتیجه می‌گیریم که غلظت کلسترول در گروه رژیم غذایی به طور معنی‌داری بیشتر از گروه ورزش است.

خب، حال بیایید از مسیر دیگری به بیان تحلیل ناپارامتری من ویتنی بپردازیم. این مسیر در ورژن‌های جدید نرم‌افزار SPSS قرار داده شده است و به نظر دارای نتایج و خروجی‌های بیشتری است.

 Analyze → Nonparametric Tests → Independent Samples 

هنگامی که از مسیر بالا جهت انجام آزمون‌های ناپارامتری در نمونه‌های مستقل استفاده می‌کنیم، پنجره زیر با نام Nonparametric Tests Two or More Independent Samples برای ما باز می‌شود. در تصویر زیر آن را ببینید.

ما با استفاده از این مسیر و پنجره تنظیمات بالا، نه فقط می‌توانیم آزمون من ویتنی که به بررسی دو گروه مستقل از یکدیگر می‌پردازد را انجام دهیم، بلکه قادر هستیم که آزمون‌های ناپارامتری دارای بیشتر از دو گروه مستقل را نیز انجام دهیم. در ادامه به توضیح هر کدام از بخش‌ها و تب‌های این پنجره می‌پردازیم.

Objective

 در این تب سه گزینه وجود دارد. انتخاب هر کدام به شما اجازه می‌دهد که هدف از آزمون ناپارامتری خود را مشخص کنید.

• Automatically compare distributions across groups

با انتخاب این گزینه به نرم‌افزار اجازه می‌دهیم، بر مبنای تعداد گروه‌های مستقل مثال، آزمون مناسب را انتخاب کند. بر این مبنا نرم‌افزار، آزمون Mann-Whitney U را برای داده‌های دارای 2 گروه مستقل و ANOVA یک طرفه Kruskal-Wallis را برای داده‌های با k گروه مستقل، اعمال می‌کند. معمولاً به صورت پیش‌فرض همین گزینه را می‌پذیریم.

• Compare medians across groups

با انتخاب این گزینه، آزمون میانه برای مقایسه میانه‌های مشاهده شده در گروه‌ها استفاده می‌شود. این گزینه برای حالتی مناسب است که شکل توزیع داده‌های کمیت وابسته، در هر کدام از گروه‌های کمیت مستقل، مشابه با یکدیگر باشد.

• Custom analysis

هنگامی که می‌خواهید تنظیمات آزمون را به صورت دستی در تب Settings اصلاح کنید، این گزینه را انتخاب کنید. انتخاب این گزینه به شما امکان می‌دهد تا کنترل دقیقی بر آزمون‌های انجام شده و گزینه‌های آنها داشته باشید. سایر آزمون‌های ناپارامتری موجود در برگه تنظیمات عبارتند از Kolmogorov-Smirnov، Moses extreme reaction، و Wald-Wolfowitz برای نمونه‌های دارای دو گروه مستقل و آزمون ناپارامتری Jonckheere-Terpstra برای نمونه‌های دارای k گروه. یک فاصله اطمینان اختیاری (براورد Hodges-Lehmann) نیز برای نمونه‌‌های با دو گروه مستقل موجود است. همه این موارد را می‌توانید در تب Settings مشاهده کنید.

با استفاده از گزینه‌های این تب، کمیت‌های وابسته و مستقل را وارد نرم‌افزار می‌کنیم.

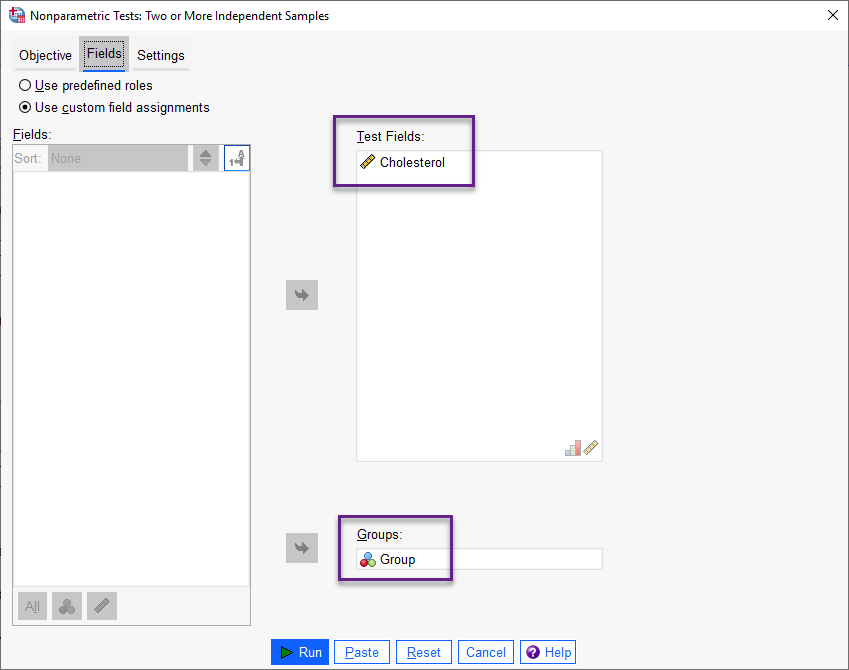
در کادر Test Fields کمیت وابسته غلظت کلسترول Cholesterol و در کادر Groups کمیت مستقل گروه‌بندی که با همان نام Groups در داده‌ها تعریف شده است، قرار می‌گیرد.

در این تب می‌توانیم انواع آزمون‌های ناپارامتری قابل انجام برای نمونه‌های مستقل را مشاهده کنیم. هنگامی که در تب Objective گزینه Automatically compare distributions across groups را انتخاب می‌کنیم، در تب Settings نیز به صورت پیش‌فرض گزینه Automatically choose the tests based on the data فعال است.

همان‌گونه که قبلاً نیز گفتیم، انتخاب این گزینه سبب می‌شود که نرم‌افزار به صورت خودکار و بر مبنای تعداد گروه‌های مستقل، آزمون آماری ناپارامتری مناسب داده‌ها را برای ما انجام دهد.

با این حال انتخاب گزینه Customize tests باعث می‌شود، به دلخواه بتوانیم آزمون ناپارامتری مورد علاقه را انجام دهیم. در تصویر زیر این آزمون‌ها را ببینید.

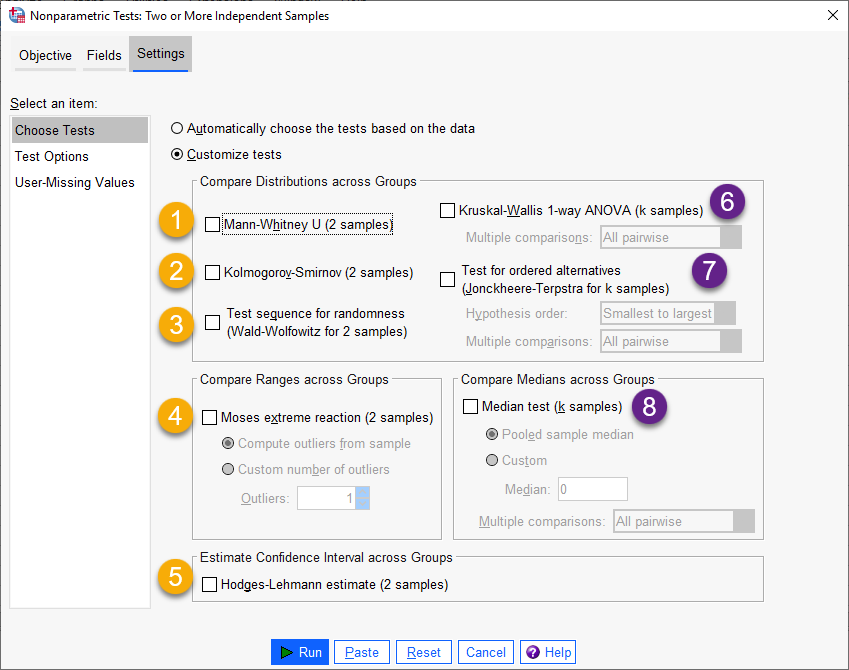
آزمون‌های ناپارامتری بالا به دو دسته کلی آزمون‌های مربوط به دو نمونه مستقل و k نمونه مستقل، تقسیم می‌شوند. من هر کدام را شماره‌گزاری کرده‌ام و در ادامه به توضیح هر یک می‌پردازم. همچنین نتایج مربوط به هر آزمون نیز که بر روی داده‌های این مثال انجام می‌شود، آمده است.

Mann-Whitney U. همان آزمون من ویتنی است که در این متن درباره‌ی آن صحبت می‌کنیم. با استفاده از آن می‌توانیم به مقایسه میانه و یا میانگین رتبه‌ها در دو گروه مستقل بپردازیم. همچنین از این آزمون می‌توان جهت تست همانندی توزیع دو نمونه مستقل، استفاده کرد.

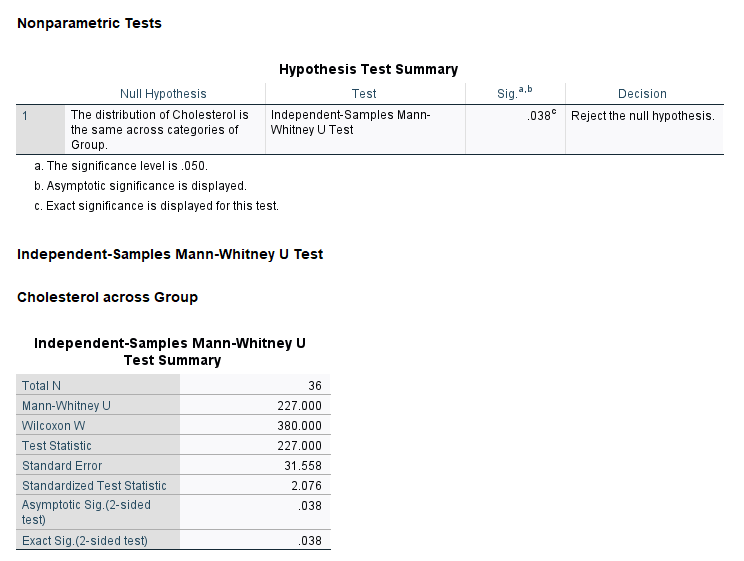
در جدول بالا، نتیجه آزمون من ویتنی آمده است. مقدار احتمال به دست آمده (P-value = 0.038) بیانگر رد فرضیه مشابه بودن توزیع داده‌های غلظت در گروه‌های رژیم غذایی و ورزش است.

در گراف زیر هیستوگرام فراوانی غلظت در هر کدام از گروه‌ها آمده است.

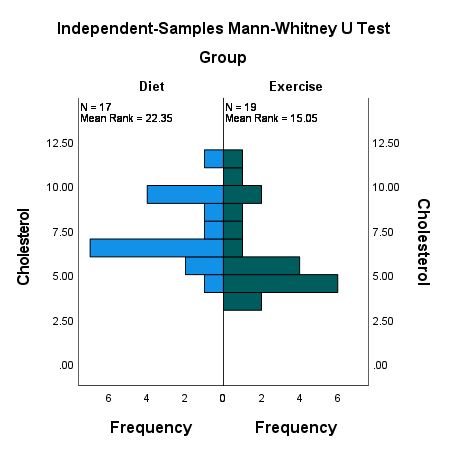
Kolmogorov-Smirnov. این آزمون برای کارهای با دو نمونه مستقل انجام می‌شود، منتهی به هرگونه تفاوت در میانه، پراکندگی، چولگی دو توزیع نمونه‌ها حساس است.

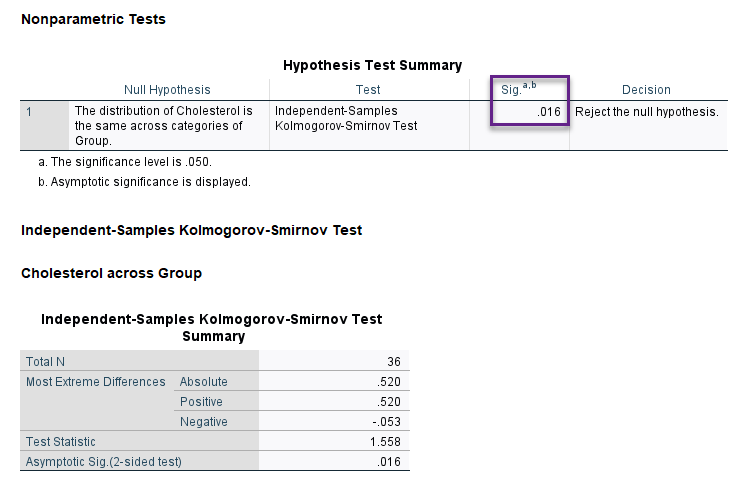
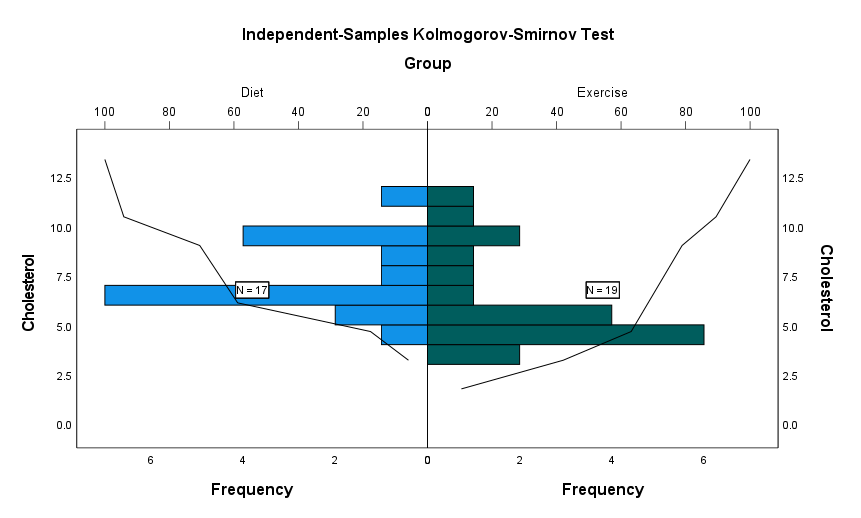
در اینجا نیز آزمون کلموگروف – اسمیرنف به دست آمده بیانگر رد فرضیه مشابه بودن توزیع داده‌ها در گروه‌های مستقل مورد بررسی است (P-value = 0.016).

Test sequence for randomness (Wald-Wolfowitz). آزمون Wald-Wolfowitz برای بررسی اینکه آیا دو نمونه تصادفی از جمعیتی با توزیع یکسان آمده اند یا خیر استفاده می‌شود. این تست می‌تواند تفاوت‌های میانگین یا پراکندگی یا هر جنبه مهم دیگری را بین دو جمعیت تشخیص دهد. در این زمینه بیشتر علاقمند بودید این مقاله را بخوانید.

در اینجا نتیجه به دست آمده از آزمون Wald-Wolfowitz از آن‌جا که بر ایده تصادفی بودن نمونه‌ها استوار است، اختلاف معنادار بین غلظت خون در گروه‌های ورزش و رژیم غذایی را نشان نمی‌دهد (P-value = 0.312).

Moses extreme reaction. این آزمون معمولاً به منظور مقایسه رنج Range و دامنه دو نمونه مستقل، استفاده می‌شود. این آزمون یکی از گروه‌ها را به عنوان گروه کنترل Control Group و دیگری را گروه آزمایش Experimental Group در نظر می‌گیرد.

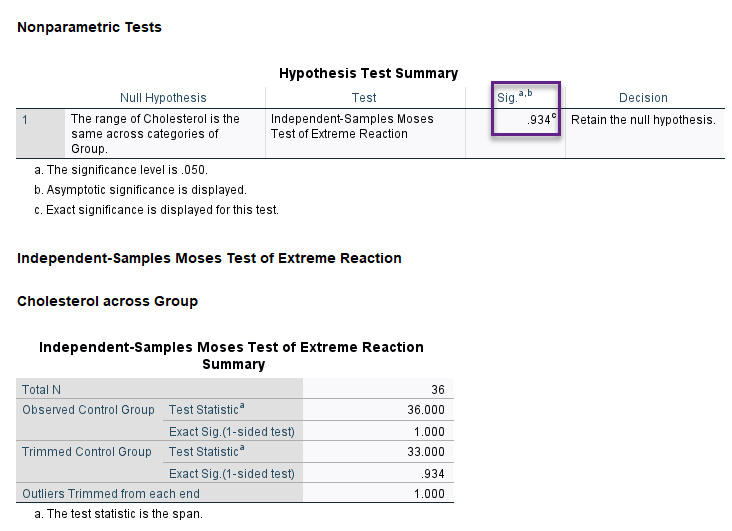
فرض صفر در این آزمون کمی متفاوت از آزمون‌‌های ناپارامتری بالا است. نتیجه به دست آمده (P-value = 0.934) نشان می‌دهد، رنج داده‌های غلظت در گروه‌های تغذیه و ورزش اختلاف معناداری با یکدیگر ندارند و در یک محدوده مشابه هستند.

Estimate Confidence Intervals across Groups. Hodges-Lehman estimate. با استفاده از این روش می‌توانیم به براورد فاصله اطمینان اختلاف بین میانه داده‌های غلظت در هر کدام از گروه‌های مستقل بپردازیم.

در اینجا بهتر است این نکته را بیان کنیم که با یک آزمون آماری به معنای واقعی آن (فرض صفر، مقابل و مقدار احتمال) روبه‌رو نیستیم. عدد 1.475 (مثبت یا منفی بودن چندان اهمیتی ندارد) نشان می‌دهد، اختلاف بین میانه غلظت کلسترول در گروه تغذیه با گروه ورزش برابر با 1.475 واحد و فاصله اطمینان 95% اختلاف بین میانه‌ها، به صورت (2.331 ,0.088) به دست می‌آید. البته در اینجا به یک نکته مهم فکر کنید و آن وجود یا عدم وجود صفر در بازه اطمینان به دست آمده است.

Kruskal-Wallis 1-way ANOVA. در این قسمت با آزمون‌های ناپارامتری دارای بیشتر از دو گروه مستقل، روبه‌رو هستیم. از آن‌جا  که این مثال مربوط به آزمون‌های با دو گروه مستقل (مانند آزمون ناپارامتری من ویتنی) است، بنابراین علاقمند بودید به لینک (آزمون ناپارامتری کروسکال والیس kruskal-Wallis 1-way ANOVA با نرم افزار SPSS) مراجعه کنید.

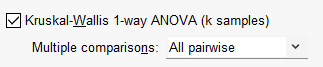
آزمون کروسکال والیس تعمیم یافته ناپارامتری آزمون Mann-Whitney هنگامی که با بیشتر از دو گروه مستقل روبه‌رو هستیم و همچنین متناظر ناپارامتری آنالیز واریانس یک طرفه است. در این مسیر می‌توانیم با استفاده از کادر Multiple comparisons به مقایسه‌های متعدد گروه‌های مستقل با یکدیگر بپردازیم.

 Test for ordered alternatives (Jonckheere-Terpstra). این آزمون جایگزین مناسبی برای Kruskal-Wallis است هنگامی که k نمونه مستقل دارای ترتیب طبیعی هستند. در این زمینه لینک (آزمون ناپارامتری Jonckheere-Terpstra با نرم افزار SPSS) را مطالعه کنید.

به عنوان مثال، k نمونه ممکن است k دمای افزایشی را نشان دهند. فرض صفر در این آزمون این است که توزیع داده‌های کمیت وابسته در هر کدام از گروه‌های کمیت مستقل، با یکدیگر مشابه است. فرض جایگزین نیز این است که با افزایش دما (به عنوان مثال)، اندازه‌های عددی کمیت پاسخ نیز افزایش می‌یابد. در واقع فرض جایگزین به صورت ترتیبی است.

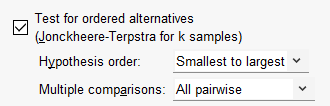
همان‌گونه که در گزینه‌های نرم‌افزار مشخص است، فرض جایگزین می‌تواند به حالت Smallest to largest باشد، که به معنای آن است که پارامتر مکان (مانند میانه) گروه اول کمتر یا مساوی با گروه دوم است و این گروه کمتر یا مساوی با گروه سوم است و به همین ترتیب.

چنانچه فرض جایگزین نیز بر روی گزینه Largest to smallest قرار بگیرد، به این معنا است که پارامتر مکان (مانند میانه) گروه اول بزرگتر یا مساوی با گروه دوم است و این گروه نیز بزرگتر یا مساوی با گروه سوم است و به همین ترتیب.

برای هر دو گزینه، فرضیه جایگزین بر این مبنا است که پارامترهای مکان گروه‌ها با هم برابر نیستند. همچنین در این آزمون نیز می‌توانیم با استفاده از کادر Multiple comparisons به مقایسه‌های متعدد گروه‌های مستقل با یکدیگر بپردازیم.

Compare Medians across Groups (Medians Test). از این آزمون جهت بررسی همانند بودن میانه‌ها (k نمونه) استفاده می‌شود. Median Test می‌تواند از میانه نمونه تلفیقی Pooled sample median (محاسبه شده بر مبنای مجموعه داده) یا یک مقدار دلخواه به عنوان میانه فرضی استفاده کند.

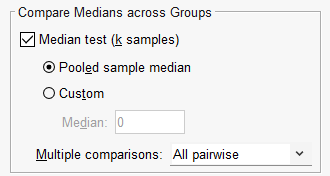
همانند آزمون ناپارامتری قبلی، در در این آزمون نیز می‌توانیم با استفاده از کادر Multiple comparisons به مقایسه‌های متعدد گروه‌های مستقل با یکدیگر بپردازیم.

در همان تب Settings و از بخش Test Options می‌توانیم به دلخواه خود سطح معناداری و فواصل اطمینان را قرار دهیم. نرم‌افزار SPSS به صورت پیش‌فرض این اعداد را به ترتیب 0.05 و 95.0 درصد قرار داده است.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2023). Mann-Whitney non-parametric test with SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/mann-whitney-spss/.php

For example, if you viewed this guide on 12^th January 2023, you would use the following reference

GraphPad Statistics (2023). Mann-Whitney non-parametric test with SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2023, from https://graphpad.ir/mann-whitney-spss/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.