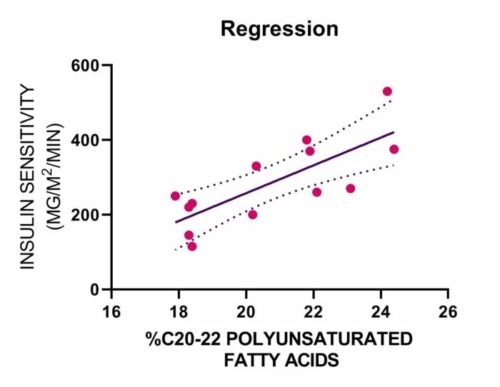
رگرسیون حداقل مربعات معمولی Ordinary Least Squares regression (OLS)
رگرسیون حداقل مربعات معمولی (OLS)، به عنوان رگرسیون خطی Linear Regression نامیده میشود. رگرسیون حداقل مربعات معمولی (OLS) تکنیک رایج برای براورد ضرایب معادلات رگرسیون خطی است که رابطه بین یک یا چند Variable مستقل و یک کمیت وابسته (رگرسیون خطی ساده یا چندگانه) را توصیف میکند.
Ordinary Least Squares regression (OLS)
حداقل مربعات Least Squares بیانگر روشی جهت مینیمم کردن مجموع مربعات خطا (SSE) Sum of Squares of Errors است. خوب است بدانیم ماکزیمم درستنمایی Maximum Likelihood و روش تعمیمیافته تخمینگر گشتاورها Generalized Method of Moments Estimator، رویکردهای جایگزین OLS هستند.
من در لینک (رگرسیون خطی Linear Regression در نرمافزار SPSS) به بیان انجام تحلیل رگرسیون خطی با استفاده از نرمافزار SPSS پرداختهام. علاقمند بودید آن را ببینید.
کمی معادله ببینیم
Equations for the Ordinary Least Squares Regression
سوالی که مطرح می شود این است که فرمول حداقل مربعات معمولی: معادله مدل چیست؟ در واقع ما در اینجا با چه فرمول رگرسیونی روبهرو هستیم؟ رابطه زیر را ببینید. مدل رگرسیونی OLS به صورت زیر نوشته میشود.
$ \displaystyle Y={{\beta }_{0}}+\sum\limits_{{i=1}}^{p}{{{{\beta }_{i}}}}{{X}_{i}}+\varepsilon $
در این رابطه، Y همان کمیت وابسته، $ \displaystyle {{\beta }_{0}}$ ضریب ثابت Intercept، $ \displaystyle {{X}_{i}}$ کمیت مستقل (i=1 to p)، $ \displaystyle {{{\beta }_{i}}}$ ضریب رگرسیونی کمیت iام و $ \displaystyle \varepsilon $ خطای تصادفی با میانگین صفر و واریانس $ \displaystyle {{\sigma }^{2}}$ است.
نکتهای که در اینجا وجود دارد و ویژگی متمایز رگرسیون OLS است، این است که براورد پارامترهای مدل رگرسیونی یعنی $ \displaystyle {{{\beta }_{i}}}$ ها به گونهای انجام میشود که $ \displaystyle \varepsilon $ یعنی خطای تصادفی رگرسیون OLS دارای میانگین صفر و واریانس $ \displaystyle {{\sigma }^{2}}$ باشد.
مثال فرض کنید میخواهیم ارتفاع گیاهان را بر مبنای تعداد روزهایی که در آفتاب سپری کردهاند پیشبینی کنیم. قبل از قرار گرفتن در معرض نور خورشید، آنها 30 سانتیمتر هستند. گیاه پس از یک روز قرار گرفتن در معرض آفتاب 1 میلی متر (0.1 سانتی متر) رشد میکند. بنابراین در اینجا گزارههای زیر را داریم.
- Y همان ارتفاع گیاه است.
- X تعداد روزهای قرار گرفته گیاه در زیر نور خورشید است.
- $ \displaystyle {{\beta }_{0}}$ برابر با 30 سانتیمتر است، زیرا مقداری از Y است اگر X = 0 باشد.
- $ \displaystyle {{\beta }_{1}}$ برابر با 0.1 سانتمتر است، زیرا اندازه رشد گیاه در اثر قرار گرفتن یک روز بیشتر در معرض آفتاب را نشان میدهد.
به عنوان مثال گیاهی که به مدت 5 روز در معرض آفتاب قرار میگیرد دارای ارتفاع براوردی Y = 30 + 0.1 * 5 = 30.5 سانتیمتر است. البته این یافته همیشه دقیق نیست، به همین دلیل باید خطای تصادفی ε را در نظر بگیریم.
نکتهای که در این میان وجود دارد این است که قبل از پیشبینی، ما باید ضرایب β را پیدا کنیم. ما فقط با وارد کردن جدولی شامل ارتفاع چند گیاه به همراه تعداد روزهایی که آنها در آفتاب سپری کردهاند، شروع میکنیم. اگر میخواهید در مورد محاسبات بیشتر بدانید، ادامه مطلب را بخوانید.
فرمولها و براورد پارامترها
How do ordinary least squares (OLS) work?
هدف روش OLS به حداقل رساندن مجموع مربعات اختلاف بین مقادیر مشاهده شده و پیشبینی شده است. یعنی در واقع میخواهیم عبارت زیر را مینیمم کنیم.
$ \displaystyle \text{to minimize}\begin{array}{*{20}{c}} {} & {{{{\sum\limits_{{j=1}}^{n}{{\left( {{{y}_{j}}-{{{\hat{y}}}_{j}}} \right)}}}}^{2}}=\sum\limits_{{j=1}}^{n}{{e_{j}^{2}}}} \end{array}$
بر این مبنا، برداز ضرایب β را به صورت زیر براورد میکنیم.
$\displaystyle \hat{\beta }={{\left( {{X}’X} \right)}^{{-1}}}{X}’Y$
$ \displaystyle \hat{Y}=X\hat{\beta }=X{{\left( {{X}’X} \right)}^{{-1}}}{X}’Y$
حتی می توانیم واریانس σ² خطای تصادفی ε را با فرمول زیر به دست بیاوریم.
$ \displaystyle {{{\hat{\sigma }}}^{2}}=\frac{{{{{\sum\limits_{{j=1}}^{n}{{\left( {{{y}_{j}}-{{{\hat{y}}}_{j}}} \right)}}}}^{2}}}}{{n-p}}=\frac{{\sum\limits_{{j=1}}^{n}{{e_{j}^{2}}}}}{{n-p}}$
در این رابطه n تعداد نمونه و p تعداد ضرایب رگرسیونی مدل OLS است.
مثال عددی
What is the intuitive explanation of the least squares method?
به طور شهودی، هدف روش حداقل مربعات معمولی به حداقل رساندن خطای پیشبینی، بین مقادیر پیشبینیشده و واقعی است. ممکن است کسی بپرسد که چرا ما به جای مینیمم کردن مجموع خطاها، مجموع مربعات خطاها را میخواهیم مینیمم کنیم.
خطاها میتوانند اعدادی مثبت و یا منفی باشد. خوب است این نکته را بدانیم که بر مبنای روش OLS، مجموع خطاها برابر با صفر است. یعنی $ \displaystyle \sum\limits_{{j=1}}^{n}{{{{e}_{j}}}}=0$
به عنوان مثال، اگر مقادیر واقعی شما 2، 3، 5، 2، و 4 و مقادیر پیشبینی شده شما 3، 2، 5، 1، 5 باشد، خطای کل به صورت زیر
$ \displaystyle \left( {5-4} \right)+\left( {1-2} \right)+\left( {5-5} \right)+\left( {2-3} \right)+\left( {3-2} \right)=1-1+0-1+1=0$
و میانگین خطا $ \displaystyle 0/5=0$ خواهد بود که میتواند منجر به نتیجهگیری نادرست شود. چرا که این نتیجه به دست میآید که ما هیچ خطایی نداریم و میانگین خطای ما صفر است.
با این حال، اگر مجموع مجذور خطا را محاسبه کنید،
$ \displaystyle {{\left( {5-4} \right)}^{2}}+{{\left( {1-2} \right)}^{2}}+{{\left( {5-5} \right)}^{2}}+{{\left( {2-3} \right)}^{2}}+{{\left( {3-2} \right)}^{2}}=4$
نتیجه خواهد شد. بنابراین میانگین مجذور خطا به صورت $ \displaystyle 4/5=0.8$ میباشد. با در نظر گرفتن جذر آن، Sqrt (0.8) = 0.89 را به دست میآوریم، بنابراین به طور متوسط، پیشبینی ما 89% با مقدار واقعی متفاوت است.
پیشفرضهای رگرسیون OLS
What are the assumptions of Ordinary Least Squares (OLS)?
جهت انجام رگرسیون حداقل مربعات معمولی Ordinary Least Squares regression (OLS) به برقراری تعدادی پیشفرض آماری نیاز است. من در ادامه آنها را آوردهام.
- پیش فرض 1
کمیت وابسته Dependent Variable که به آن پاسخ Response و Y نیز گفته میشود، باید در مقیاس پیوسته Scale اندازهگیری شوند. به عنوان مثال زمان (برحسب ساعت)، هوش (با استفاده از نمره IQ)، عملکرد امتحان (از 0 تا 100)، وزن (برحسب کیلوگرم) و غیره.
- پیش فرض 2
کمیتهای مستقل Independent Variables که به آنها پیشبینی کننده Predictor و یا X گفته میشود، نیز باید به صورت پیوسته Continuous اندازهگیری شده باشند.
- پیش فرض 3
باید یک رابطه خطی linear relationship بین X و Y وجود داشته باشد. در حالی که روشهای مختلفی برای بررسی رابطه خطی وجود دارد، پیشنهاد میکنیم با استفاده از نمودارهای پراکنش Scatter Plots استفاده کنید. در این لینک (رسم نمودار پراکنش Scatter Plot با استفاده از نرمافزار SPSS) میتوانید آموزش رسم آنها را ببینید. با استفاده از این گرافها میتوانید به صورت بصری پراکندگی دادهها را به منظور خطی بودن بررسی کنید. نمودار پراکندگی شما ممکن است چیزی شبیه به یکی از موارد زیر باشد.
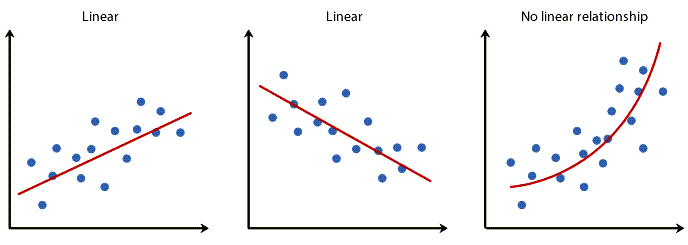
اگر رابطه نمایش داده شده در نمودار پراکندگی شما خطی نیست، باید یک تحلیل رگرسیون غیرخطی انجام دهید، یک رگرسیون چند جملهای Polynomial Regression انجام دهید یا دادههای خود را تبدیل کنید، این کار را میتوانید با استفاده از SPSS انجام دهید.
- پیش فرض 4
نباید نقاط پرت Outliers قابل توجهی وجود داشته باشد. نقطه پرت یک نقطه داده مشاهده شده است که عدد پاسخ آن با مقدار پیشبینی شده توسط معادله رگرسیون بسیار متفاوت است. به این ترتیب، نقطه پرت نقطهای در یک نمودار پراکنش خواهد بود که (به صورت عمودی) از خط رگرسیون دور است و نشان میدهد که باقیمانده Residual و خطای زیادی دارد، گرافهای زیر را ببینید.
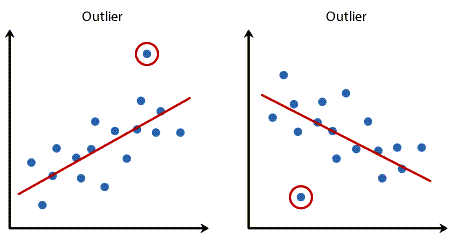
مشکل دادههای پرت این است که میتوانند تاثیر منفی بر تحلیل رگرسیون داشته باشند (به عنوان مثال، تناسب معادله رگرسیون را کاهش دهند) که برای پیشبینی مقدار کمیت وابسته (پاسخ) بر اساس کمیت مستقل (پیشبینی کننده) استفاده میشود. وجود دادههای پرت دقت پیشبینی نتایج شما را کاهش میدهند. خوشبختانه، هنگام استفاده از SPSS برای اجرای رگرسیون خطی، میتوانید به راحتی معیارهایی را برای کمک به تشخیص موارد پرت در نظر بگیرید. با استفاده از تشخیص موردی casewise diagnostics که یک فرآیند ساده هنگام استفاده از SPSS است، میتوانید نقاط پرت را تشخیص دهید. علاقمند بودید در این لینک (آزمون دوربین واتسن Durbin-Watson و تشخیص موردی Casewise diagnostics) میتوانید آموزش آن را ببینید.
همچنین با استفاده از رسم نمودارهای جعبهای که آموزش آن را میتوانید در این لینک ببینید (رسم Box Plot با استفاده از نرمافزار SPSS) میتوانیم به شناسایی و یافتن دادههای پرت، اقدام کنیم. در این زمینه میتوانید این آموزش را هم ببینید. (تشخیص داده پرت با استفاده از Grubbs’ Test در Minitab)
- پیش فرض 5
مشاهدات باید از یکدیگر مستقل باشند. این کار را به سادگی میتوانید با استفاده از آزمون دوربین-واتسن Durbin-Watson بررسی کنید. در این زمینه لینک (آزمون دوربین واتسن Durbin-Watson و تشخیص موردی Casewise diagnostics) را ببینید.
- پیش فرض 6
یکی دیگر از پیشفرضهای انجام تحلیل رگرسیون خطی برقرار بودن مفهومی به اسم هم واریانسی و یا Homoscedasticity است. در این زمینه توصیه میکنم حتماً مقاله آزمونهای ناهم واریانسی Heteroscedasticity Tests در نرم افزار SPSS را مطالعه کنید.
هم واریانسی به این معنا است که باید خطای مدل که به آن Residual و باقیمانده هم گفته میشود، دارای ثبات در واریانس باشد. مفهوم ثبات در واریانس هم به معنای این است که خطاهای مدل نباید با مقادیر عددی برازش شده برای Dependent Variable یا همان کمیت پاسخ، مرتبط و وابسته باشند.
به نمودارهای پراکندگی زیر که سه مثال ساده ارایه میدهند نگاه کنید. دو مورد از دادههایی که این فرض را نقض میکنند (به نام ناهم واریانسی Heteroscedasticity) و یک مورد از دادههایی که این فرض را برآورده میکند (به نام هم واریانسی Homoscedasticity).
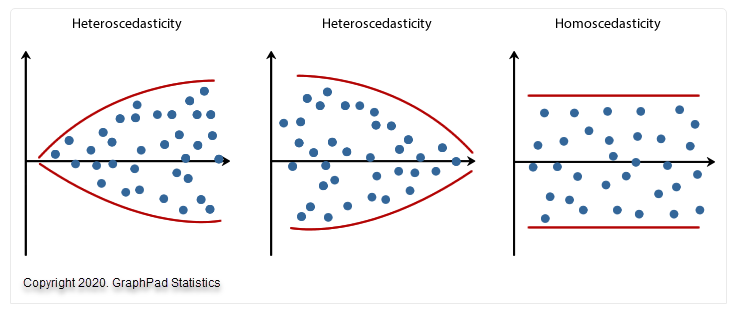
- پیش فرض 7
باقیماندهها یا همان Residuals باید به طور تقریبی نرمال باشند (Approximately Normally). در اینجا یک نکته بسیار مهم وجود دارد. آنالیز رگرسیون خطی نسبت به نقض فرض نرمال بودن باقیماندهها اصطلاحا استوار Robust است. به این معنی که این فرض میتواند تا حدی نقض شود و همچنان نتایج معتبری ارایه دهد. ما با استفاده از نمودار احتمال نرمال میتوانیم به بررسی این فرض بپردازیم. علاقمند بودید لینک (نمودار احتمال نرمال Normal Probability Plot در مدل های رگرسیونی) را ببینید. همچنین در این زمینه لینک بررسی نرمال بودن دادهها را مشاهده کنید (آزمون نرمال بودن دادهها Normality Test در نرمافزار SPSS).
محدودیتها و مزایای OLS
What are the advantages and limitations of OLS?
قبل از اینکه بخواهم دربارهی امتیازات و ویژگیهای رگرسیون OLS صحبت کنم، خوب است بدانید محدودیتهای رگرسیون OLS از محدودیت وارونگی ماتریس X’X ناشی می شود: به خاطر داشته باشید ما در براورد ماتریس ضرایب همبستگی از وارون ماتریس X’X استفاده میکنیم. لازم است که رتبه ماتریس X’X برابر با p+1 باشد و اگر اینگونه نباشد برخی مشکلات عددی در براورد مانریس β ایجاد میشود.
از مزایای رگرسیون OLS مفهومی به نام انتخاب کمیتها Selection Variables است. من در لینک (Selection Variable در مدل های رگرسیونی) در این موضوع توضیح دادهام. انتخاب خودکار کمیتها در صورتی انجام میشود که کاربر تعداد بالایی از Variable ها را در مقایسه با تعداد مشاهدات انتخاب کند. از نظر تئوری تعداد Variableها میتواند تا n-1 باشد، زیرا با مقادیر بیشتر، ماتریس X’X غیرقابل تبدیل میشود.
حذف برخی از کمیتها ممکن است بهینه نباشد. در برخی موارد ممکن است لازم باشد کمیتی را به مدل اضافه نکنیم زیرا با برخی از Variableهای دیگر هم خطی داشته باشد. در این زمینه علاقمند بودید لینک (تشخیص هم خطی Collinearity Diagnostics در مدل های رگرسیونی) را ببینید.
به همین دلیل و همچنین بررسی مواردی که Variableهای توضیحی یعنی کمیتهای مستقل زیادی در مدل رگرسیونی وجود دارد، روشهای دیگری مانند رگرسیون حداقل مربعات جزئی Partial Least Squares regression (PLS) توسعه یافته و به وجود آمده است.
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2022). Ordinary Least Squares regression. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/ordinary-least-squares-regression/.php
For example, if you viewed this guide on 12th January 2022, you would use the following reference
GraphPad Statistics (2022). Ordinary Least Squares regression. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/ordinary-least-squares-regression/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.