آزمون روند خطی Test for Linear Trend در نرم‌افزار Prism

 Test for Linear Trend 

دریافت آموزش تحلیل‌های مقایسه‌ای با Prism

شامل 150 دقیقه ویدئو، فایل‌های مثال، دیتا و نتایج نرم‌افزار Prism

شاید برای شما جالب باشد که بگویم آزمون روند خطی Test for Linear Trend اصولاً یک روش تحلیل مقایسه‌ای است و در رده آزمون‌های آنالیز واریانس قرار می‌گیرد.

من در ادامه و در این مقاله به بیان تعریف و نحوه‌ی انجام این آزمون با استفاده از نرم‌افزار Prism می‌پردازم.

آزمون روند خطی

 Test for Linear Trend 

برای فهم آزمون روند خطی بیایید از اینجا شروع کنیم که آنالیز واریانس (یکطرفه) چیست؟ پاسخ این است هنگامی که می‌خواهیم یک Dependent را در بین گروه‌های مختلف یک Independent مقایسه کنیم، از One-way ANOVA استفاده می‌کنیم. در این لینک می‌توانید اطلاعات بیشتری درباره‌ی آنالیز واریانس یک طرفه به دست آورید.

حال اگر این گروه‌ها، ترتیبی و رتبه‌ای باشند مثلاً گروه‌های سنی، دوزهای مختلف دارو و یا زمان‌های مختلف، در این صورت استفاده از آزمون روند خطی به ما نشان می‌دهد که آیا بین گروه‌ها روند افزایشی (یا کاهشی) معنادار وجود دارد یا خیر. در واقع آنالیز واریانس وجود اختلاف بین گروه‌ها را به نشان می‌دهد و آزمون روند خطی وجود روند بین گروه‌ها را.

Prism می‌تواند روند خطی را به عنوان بخشی از آزمایش پیگیری پس از ANOVA یک طرفه (اما نه دو یا سه طرفه) آزمایش کند. این یک انتخاب در تب Multiple Comparisons تنظیمات ANOVA یک طرفه است.

نکته توجه داشته باشید که محاسبات ANOVA (به جز این تست روند) به طور کامل ترتیب نوشته شدن ستون‌ها (گروه‌ها) در نرم‌افزار را نادیده می‌گیرد. می‌توانید به‌طور تصادفی ترتیب ستون‌ها را به هم بزنید و دقیقاً همان نتایج ANOVA را دریافت کنید. بنابراین اگر ستون‌ها نقاط زمانی یا غلظت‌ها یا هر چیزی را نشان می‌دهند که می‌توان آن‌ها را به صورت عددی گزارش کرد، خوب فکر کنید که آیا ANOVA بهترین راه برای تحلیل داده‌های شما است یا خیر. اگر گروه‌ها را می‌توان به صورت عددی گزارش کرد، (مثلاً دوزهای دارو) بنابراین بهتر است به جای انجام ANOVA و به دنبال آن آزمون روند خطی، داده‌ها را با رگرسیون خطی (یا غیر خطی) برازش دهید.

خب، حال بیایید در موضوع این مقاله یعنی آزمون روند خطی، یک مثال با همدیگر ببینیم.

داده‌های زیر را که در بخش Column نرم‌افزار Prism وارد شده است، مشاهده می‌کنید. این داده‌ها اندازه‌گیری یک کمیت عددی در بین گروه‌های سنی مختلف را نشان می‌دهد. می‌دانیم که با استفاده از آزمون One-way ANOVA می‌توانیم دریابیم که آیا کمیت عددی در بین گروه‌های سنی، متفاوت است یا خیر. در واقع آنالیز واریانس یک طرفه در اینجا به ما کمک می‌کند که بفهمیم آیا سن عامل اثرگزاری بر این کمیت عددی هست یا نیست.

با این حال همان‌گونه که قبلاً نیز گفتیم در این مقاله در پی این هستیم که دریابیم آیا یک روند افزایشی (یا کاهشی) در بین گروه‌های سنی مشاهده می‌شود یا خیر. به عبارت دیگر سوال ما این است که آیا کمیت مورد بررسی با افزایش سن (همان‌گونه که مشاهده می‌کنید گروه‌های سنی به ترتیب افزایش کنار هم قرار گرفته‌اند)، روند افزایشی (یا کاهشی) دارد یا ندارد. فایل دیتا این مثال را می‌توانید از اینجا Test for Linear Trend دریافت کنید. در تصویر زیر داده‌ها را مشاهده می‌کنید.

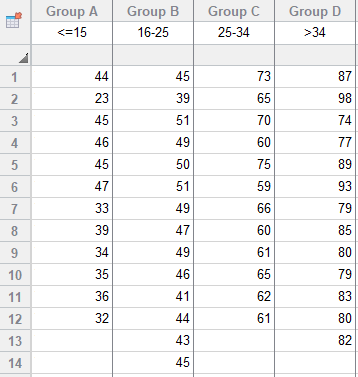
آزمون روند خطی یکی از گزینه‌های موجود در آنالیز واریانس نرم‌افزار Prism است. این گزینه با نام Test for linear trend between column mean and left-to-right column order در تب Multiple Comparisons پنجره‌ی Parameters One-Way ANOVA قرار دارد.

از مسیر زیر می‌توانیم آن را ببینیم.

 Analyze → Column Analyses (One-way ANOVA) → Multiple Comparisons  

در ادامه نتایج و خروجی‌های نرم‌افزار آمده است.

نتایج آزمون

 Results 

هنگامی که OK می‌کنیم در بخش Results یک شیت جدید با نام Test for trend ایجاد می‌شود. در تصویر زیر می‌توانید آن را ببینید.

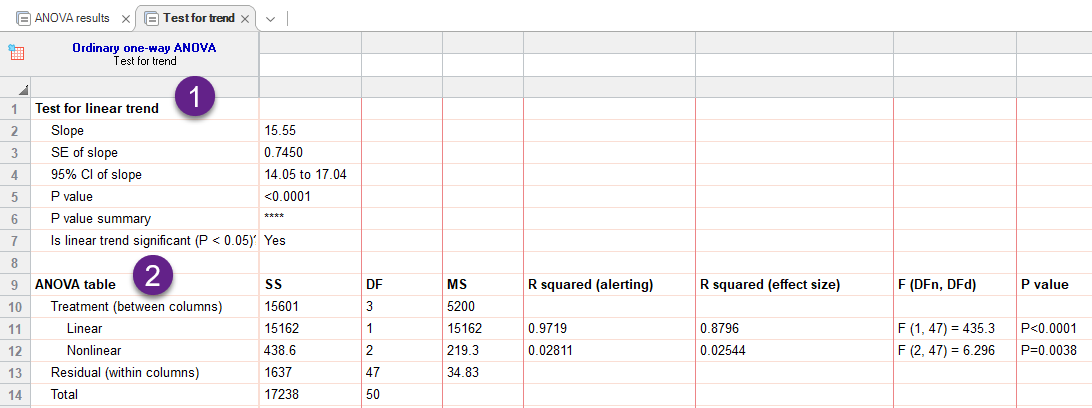
این شیت از نتایج که به بررسی آزمون روند خطی می‌پردازد، دارای بخش‌های با نام Test for linear trend و ANOVA table است. من آن‌ها را شماره گزاری کرده و در ادامه به توضیح هر یک می‌پردازم.

 1  بخش با نام Test for linear trend نتایج موثر مربوط به آنالیز روند خطی را نشان می‌دهد.

Slope یا شیب، میزان عوض شدن مقدار میانگین با رفتن از یک ستون به ستون دیگر سمت راست است. هر چقدر این عدد بزرگتر باشد (در این مثال Slope = 15.55 به دست آمده است) به معنای وجود روند قوی‌تر در بین ستون‌ها (گروه‌ها) خواهد بود. مقادیر شیب نزدیک به صفر، نشان‌دهنده عدم وجود روند در بین گروه‌ها است.

نرم‌افزار Prism جهت محاسبه این شیب از کتاب زیر صفحات 952-940

Altman, D. G. 1991 Practical statistics for medical research.  Chapman and Hall

و همچنین کتاب زیر صفحات 213-212 و 220-219 استفاده می‌کند.

علاقمند بودید به این کتاب‌ها می‌توانید مراجعه کنید.

در ادامه نتایج نرم‌افزار در این بخش، انحراف خطا از شیب SE of Error و فواصل اطمینان 95 درصد برای شیب نیز به دست آمده است.

آنچه در نتایج این بخش اهمیت دارد و ما به دنبال آن بودیم، آزمون روند خطی در بین ستون‌ها (در این مثال منظور از ستون‌ها همان گروه‌های سنی است) می‌باشد. فرض صفر در این آزمون، عدم وجود روند خطی و فرض مقابل بیانگر وجود رابطه خطی است. مقدار احتمال به دست آمده P-value < 0.0001 نشان می‌دهد فرض صفر رد شده و می‌پذیریم که یک روند خطی در بین گروه‌های سنی دیده می‌شود.

مشاهده‌ی آماره‌های توصیفی و به ویژه میانگین کمیت مورد بررسی در هر کدام از گروه‌های سنی (جدول زیر) به ما این نکته را نشان می‌دهد که روند معنادار و تایید شده بین گروه‌ها، به صورت یک روند افزایشی و صعودی خود را نشان می‌دهد. به طوری که میانگین در گروه سنی پانرده سال و کمتر، از عدد 38.25 در یک روند صعودی، به عدد 83.54 سال در گروه سنی بالاتر از 34 سال، رسیده است.

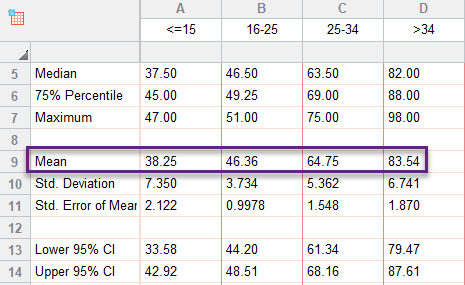
 2  بخش دیگر نتایج با نام ANOVA table دیده می‌شود.

در این جدول نتایج آنالیز روند خطی و یک تحلیل روند غیرخطی که نرم‌افزار آن را انجام می‌دهد، آمده است. موضوع مهم در این خروجی R square ها و P value ها می‌باشد. نرم‌افزار برای هر کدام از آنالیزهای خطی و غیرخطی این نتایج را جداگانه ارایه می‌کند.

ابتدا بیایید از R square ها شروع کنیم. همان‌گونه که از رگرسیون می‌دانیم این اعداد در بازه بین صفر تا یک قرار دارند. در اینجا دو R square یکی با نام R squared (alerting) و دیگری با نام R squared (effect size) گزارش شده است.

R squared (alerting) در واقع کسری از واریانس بین میانگین‌های گروهی است که با روند خطی (و غیرخطی) محاسبه می‌شود.

به همین ترتیب R squared (effect size) کسری از کل واریانس است که توسط روند خطی (و غیرخطی) محاسبه می‌شود.

از آنجایی که واریانس بین میانگین‌های گروه، همیشه کمتر از واریانس کل است، بنابراین R squared (alerting) همیشه بالاتر از اندازه اثر R squared (effect size) است.

هر چقدر اعداد R square بیشتر باشد به معنای وجود روند قوی‌تر (خطی یا غیرخطی) در داده‌ها می‌باشد. در این مثال اندازه‌های R squared (alerting) = 0.9719 و R squared (effect size) = 0.8796 بیانگر وجود روند خطی قوی در بین گروه‌های سنی می‌باشد. قبلاً نشان دادیم که این روند صعودی و افزایشی است.

به همین ترتیب در جدول ANOVA table دو مقدار احتمال P value مشاهده می‌شود. یکی برای Linear و دیگری برای Nonlinear.

مقدار احتمال روند خطی که عدد آن در این مثال به صورت P value < 0.0001 به دست آمده است، این فرضیه صفر را آزمایش می‌کند که هیچ روند خطی بین میانگین و ترتیب گروه‌ها وجود ندارد. اگر مقدار P کوچک است، نتیجه بگیرید که یک روند خطی معنی دار آماری وجود دارد. یعنی هنگامی که در جدول داده‌ها از چپ به راست می‌روید، گروه‌ها تمایل به بالاتر (یا پایین‌تر شدن) دارند.

مقدار احتمال روند غیرخطی که مقدار آن در این مثال برابر با P value = 0.0038 به دست آمده است، نشان می‌دهد که احتمالاً (علاوه بر روند خطی) یک روند غیرخطی نیز در بین میانگین و ترتیب ستون‌ها وجود دارد.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2023). Test for Linear Trend in Prism software. Statistical tutorial and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/test-for-linear-trend-prism/.php

For example, if you viewed this guide on 12^th January 2023, you would use the following reference

GraphPad Statistics (2023). Test for Linear Trend in Prism software. Statistical tutorials and software guides. Retrieved January, 12, 2023, from https://graphpad.ir/test-for-linear-trend-prism/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.