مدل رگرسیون پواسن Poisson Regression در نرم‌افزار SPSS

 Poisson Regression 

هنگامی که می‌خواهیم داده‌های خود را با استفاده از رگرسیون پواسون تحلیل کنیم، لازم است برخی از پیش‌فرض‌های این آنالیز را بدانیم. بیان این نکته لازم است هنگامی می‌توانیم و مناسب است که از Poisson Regression استفاده کنیم که این پیش‌فرض‌ها برقرار باشد. البته آن‌ها مطلب پیچیده‌ای نیستند و در اغلب مطالعات دارای کمیت وابسته شمارشی (دارای توزیع پواسن) دیده می‌شوند. بیایید یکبار آن‌ها را مرور کنیم.

 پیش‌فرض 1.   واضح است هنگامی که می‌خواهیم از مدل رگرسیون پواسن استفاده کنیم، کمیت پاسخ باید از نوع شمارش، فراوانی و تعداد باشد. به این نکته دقت کنید که اگر تعداد واحدهای شمارش زیاد باشد، بهتر است از مدل رگرسیون دیگری مانند خطی و یا گاما استفاده کنید.

 پیش‌فرض 2.   هنگامی که از رگرسیون نام می‌بریم لازم است، کمیت‌های مستقل یا همان X ها نیز در مدل باشند. بنابراین در یک مدل رگرسیون پواسن باید یک یا چند Independent Variable (IV) وجود داشته باشد. IV ها می‌توانند عددی، رتبه‌ای و یا اسمی باشند. آن‌ها عوامل اثرگزار بر DV هستند که ما می‌خواهیم میزان و چگونگی تاثیر آن‌ها بر کمیت پاسخ را به دست بیاوریم.

 پیش‌فرض 3.   مشاهدات باید از یکدیگر مستقل باشند. یعنی یک مشاهده نمی‌تواند اطلاع و یافته‌ای در مورد مشاهده دیگر ارایه دهد. این یک فرض بسیار مهم است. به این نکته توجه کنید که فقدان مشاهدات مستقل بیشتر یک موضوع طراحی مطالعه است.

 پیش‌فرض 4.   داده‌های کمیت پاسخ باید دارای توزیع پواسن Poisson Distribution باشند. فرضیه پواسن بودن داده‌ها را به سادگی با استفاده از یک آزمون نیکویی برازش Goodness of fit می‌توان انجام داد. در این زمینه می‌توانید این لینک را ببینید.

 پیش‌فرض 5.   یکی از ویژگی‌های توزیع پواسن، برابر بودن میانگین و واریانس در داده‌های مرتبط با ان است. بنابراین هنگامی که می‌خواهید از مدل رگرسیون پواسن استفاده کنید، مقادیر عددی آماره‌های توصیفی آن را بررسی کنید. البته هنگامی که روی داده‌های واقعی کار می‌کنیم، بسیار کم اتفاق می‌افتد که میانگین و انحراف معیار دقیقاً یکسان باشند (حتی با وجود تایید فرضیه پواسن بودن داده‌ها). به دلیل اینکه همیشه در داده‌های واقعی مقداری انحراف از توزیع پواسن (یا هر توزیع آماری دیگری) وجود دارد و به همین دلیل P-value وجود دارد و گزارش می‌شود. بنابراین می‌توان پیش‌فرض شماره 5 را اینگونه نوشت که میانگین و واریانس داده‌ها در نزدیکی قابل قبول از یکدیگر باشند.

من در مقاله با عنوان انواع مدل‌های خطی تعمیم یافته GLM و GEE در نرم‌افزار SPSS، به بیان مدل‌های موجود در نرم‌افزار پرداختم. مدل رگرسیون پواسن که می‌خواهم در این مقاله درباره‌ی آن صحبت کنم، یکی از همان انواع مدل‌های تعمیم است. بنابراین ابتدا این مقاله را مطالعه کنید. حال بیایید با یک مثال از رگرسیون پواسن شروع کنیم.

 

مثال رگرسیون پواسن

 Example 

در یک مطالعه که بر روی 100 نفر انجام شده، نتایجی مانند تعداد عود تومور به ازای هر بیمار، گروه درمانی، تعداد و اندازه بزرگترین تومور هر فرد در ابتدای مطالعه به دست آمده است.

هدف ما در این مطالعه این است که رابطه‌ای بین تعداد تومور با نوع گروه درمانی، تعداد و سایز تومور ابتدای مطالعه، به دست بیاوریم. از آن‌جا که کمیت پاسخ ما تعداد و شمارش است که دارای توزیع پواسن می‌باشد، بنابراین از مدل‌های رگرسیون پواسن استفاده می‌کنیم. در تصویر زیر بخشی از داده‌های این مثال را مشاهده می‌کنید.

فایل دیتا این مقاله را می‌توانید از اینجا Poisson Regression دریافت کنید.

 

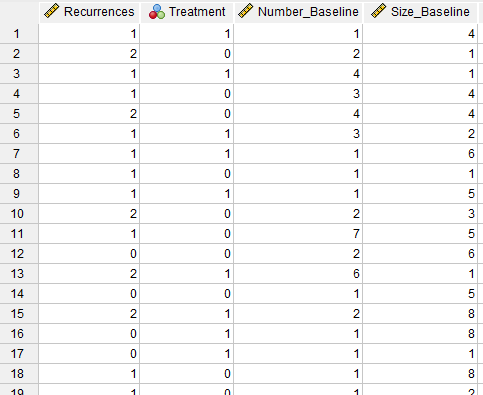
همان‌گونه که مشاهده می‌کنید داده‌ها در چهار ستون بیان شده‌اند. ستون با نام Recurrences همان کمیت پاسخ Y مدل رگرسیون پواسن است که خود دارای توزیع پواسن است و تعداد عود تومور به ازای هر بیمار را نشان می‌دهد.

ستون Treatment نشان می‌دهد فرد در گروه درمان با کد 1 و یا در گروه کنترل با کد صفر قرار دارد.

ستون Number of Tumors at Baseline و Size of Largest Tumor at Baseline به ترتیب نشان‌دهنده‌ی تعداد و اندازه بزرگترین تومور هر فرد در ابتدای مطالعه می‌باشند.

جهت به دست آوردن مدل رگرسیون پواسن در نرم‌افزار SPSS از مسیر زیر استفاده می‌کنیم.

Analyze → Generalized Linear Models → Generalized Linear Models 

 

تنظیمات نرم‌افزار در مدل پواسن

 Setting 

هنگامی که به مسیر بالا در نرم‌افزار SPSS می‌رویم، پنجره زیر با نام Generalized Linear Models برای ما باز می‌شود.

 

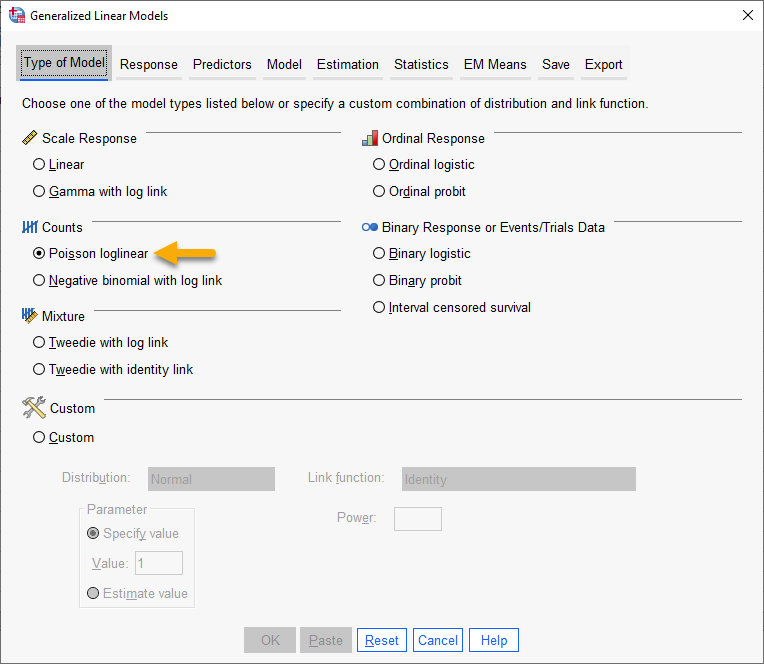
در این پنجره و از بخش Counts گزینه Poisson loglinear را انتخاب می‌کنیم. انتخاب این گزینه و این بخش به این دلیل است که داده‌های کمیت پاسخ ما از نوع شمارشی و دارای توزیع پواسن است. در ادامه من درباره‌ی سایر تب‌های مورد نیاز در این پنجره صحبت می‌کنم.

بر روی تب  بزنید. وارد پنجره زیر می‌شوید.

 

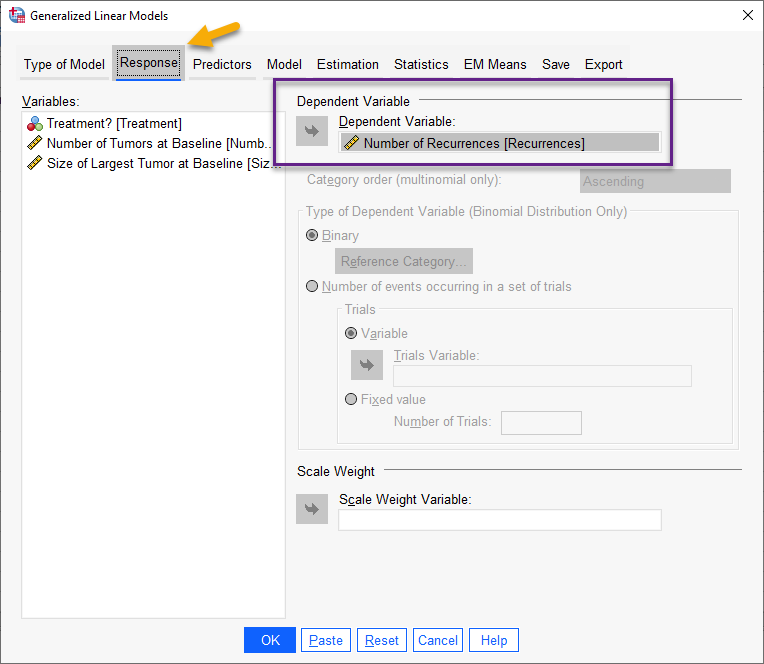
در این تب لازم است، کمیت پاسخ Response مدل رگرسیون پواسن، تعیین شود. از آن‌جا که ما می‌خواهیم رابطه بین تعداد عود تومور و سایر Xها را به دست بیاوریم، بنابراین ستون با نام Number of Recurrences را در کادر Dependent Variable قرار می‌دهیم.

بر روی تب  بزنید. در این صورت وارد پنجره زیر می‌شوید.

 

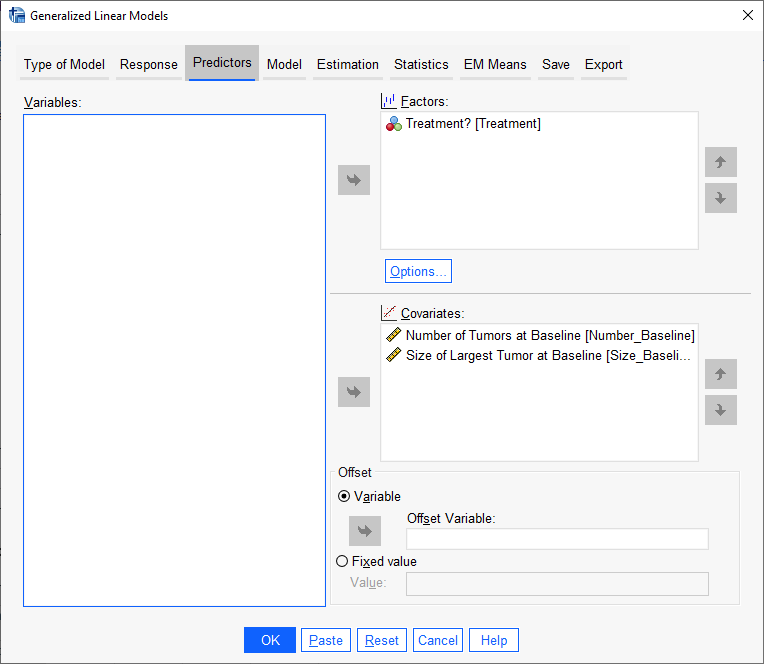
در تب Predictors لازم است X های مدل رگرسیون پواسن را به نرم‌افزار معرفی کنیم. معمولاً کمیت‌های اسمی و گاهی اوقات رتبه‌ای به عنوان Factor و کمیت‌های عددی Scale به عنوان Covariate در این مدل قرار می‌گیرند. ما هم در پنجره بالا همین کار را انجام دادیم. یعنی Treatment که نشان‌دهنده گروه درمان یا کنترل است در بخش Factors و تعداد و اندازه تومور در بخش Covariates قرار می‌گیرند.

در این پنجره بخش دیگری با نام Offset دیده می‌شود. در توضیح این مطلب بیان می‌کنیم که اصطلاح Offset به معنای یک پیش‌بینی کننده “ساختاری” است. یعنی وارد مدل می‌شود اما ضریب رگرسیونی آن توسط مدل براورد نمی‌شود، ورود آن نیز به مدل به دلیل این است که بتواند به بهبود براورد سایر X های موجود در مدل کمک کند. این مطلب به ویژه در مدل‌های رگرسیون پواسون که هر فرد می‌تواند سطح متفاوتی از قرار گرفتن در معرض رویداد مورد علاقه (در اینجا عود تومور) را داشته باشد، مفید است.

به عنوان مثال در اینجا سن بیمار می‌تواند به عنوان یک Offset Variable وارد مدل شود. به دلیل اینکه تفاوت مهمی در احتمال عود تومور بین فردی با سن 70 سال و فردی با سن 30 سال وجود دارد. به این نکته نیز دقت کنید که اگر کمیتی به عنوان Offset‌ در نظر گرفته شود دیگر نمی‌تواند به عنوان Covariate و یا Factor وارد مدل شود. وارون این موضوع نیز برقرار است.

در مرحله‌ی بعد بر روی تب  بزنید تا وارد پنجره زیر شوید.

 

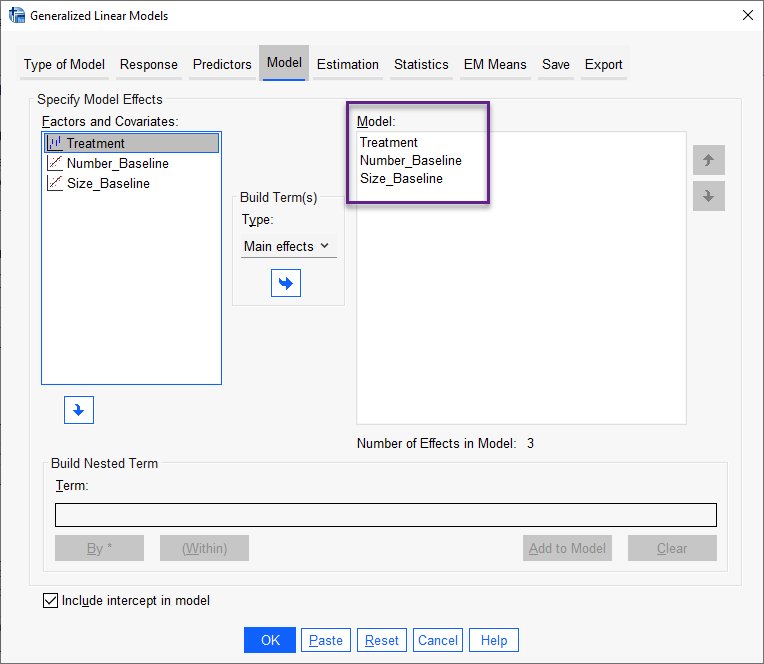
در این پنجره هر سه X مدل رگرسیون پواسن یعنی درمان، تعداد و اندازه تومور را در کادر Model قرار می‌دهیم.

همچنین صرفاً می‌خواهیم اثرات اصلی Main effects آن‌ها را به دست بیاوریم و با Interactionها مثلا اثر متقابل درمان*سایز و یا اثر متقابل تعداد*سایز کاری نداریم. به همین دلیل در بخش Type گزینه Main effects را انتخاب می‌کنیم. تیک گزینه Include intercept in model را هم که به صورت پیش فرض نرم‌افزار SPSS قرار دارد، انتخاب می‌کنیم.

در این پنجره، بخشی با عنوان Build Nested Term وجود دارد. در این روش می‌توانید فاکتورهای تو در تو (آشیانه‌ای) برای مدل خود بسازید. اثرات تو در تو برای مدلسازی اثر یک عامل یا کمیت کمکی که مقادیر آن با سطوح عامل دیگر برهمکنش ندارد مفید هستند. به عنوان مثال، یک فروشگاه زنجیره‌ای مواد غذایی ممکن است میزان هزینه خرید مشتریان خود را در چندین مکان فروشگاه دنبال کند. از آنجایی که هر مشتری فقط در یکی از این مکان‌ها خرید کرده است، می‌توان گفت که تاثیر مشتری درون تاثیر مکان فروشگاه قرار دارد. بنابراین مکان فروشگاه می‌تواند به عنوان یک Nested Variable وارد مدل شود.

در تب Estimation روش‌ها و گزینه‌ةای جهت براورد پارامترهای مدل قرار دارد. در تصویر زیر ببینید.

 

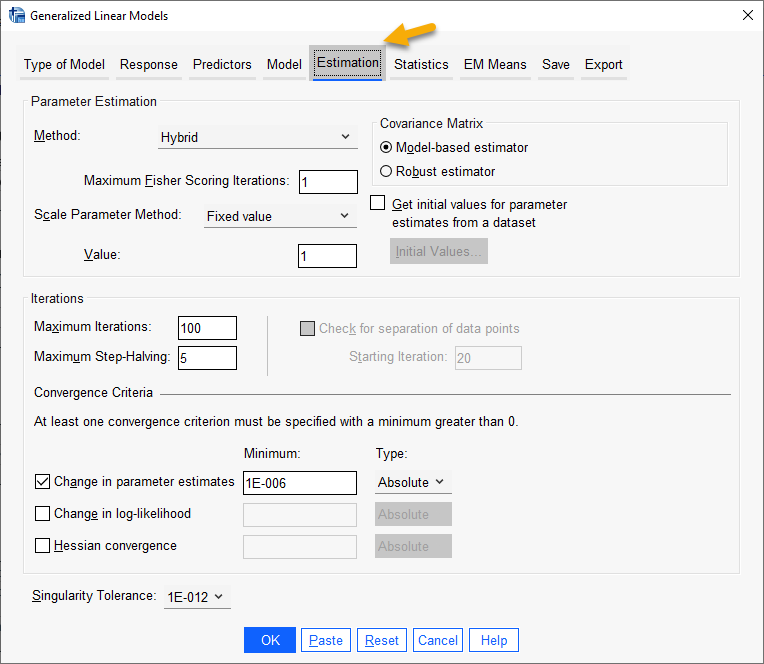
معمولاً گزینه‌های پیش‌فرض نرم‌افزار در این پنجره انتخاب و قرار داده می‌شود. در این موضوع علاقمند بودید این لینک را در سایت IBM ببینید.

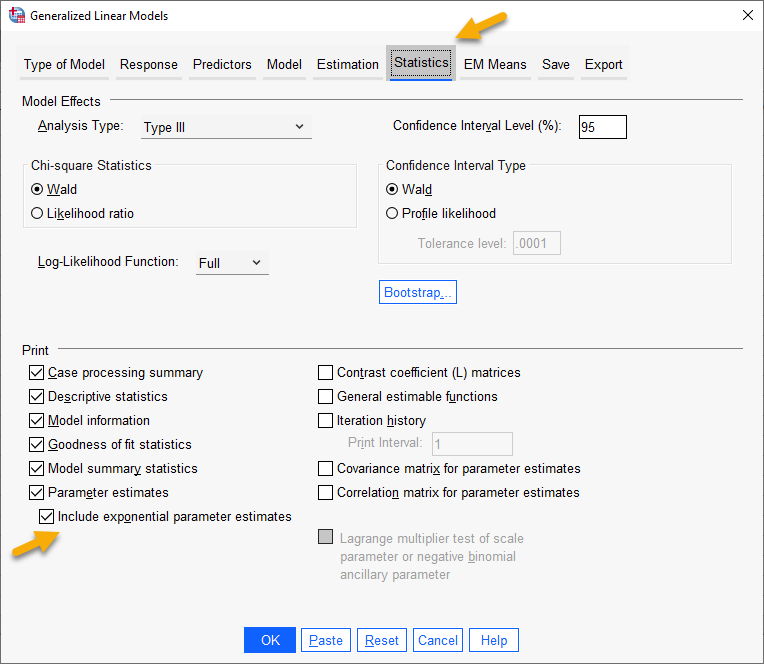
همچنین در پنجره زیر می‌توانید تب Statistics را مشاهده کنید. ما گزینه‌های پیش‌فرض نرم‌افزار در این تب را نیز می‌پذیریم و قرار می‌دهیم. من در اینجا علاوه بر تنظیمات نرم‌افزار گزینه Include exponential parameter estimates را هم انتخاب کرده‌ام. در این زمینه علاقمند بودید این لینک را ببینید.

 

در تب EM Means می‌توانیم میانگین‌های حاشیه‌ای Marginal Means براورد شده برای هر کدام از گروه‌ها و سطوح مختلف فاکتورهای موجود در مدل و یا اثرات متقابل مدل را مشاهده کنیم. ما همچنین در این تب می‌توانیم به مقایسه سطوح و گروه‌های مختلف اثرات متقابل با یکدیگر بپردازیم.

 

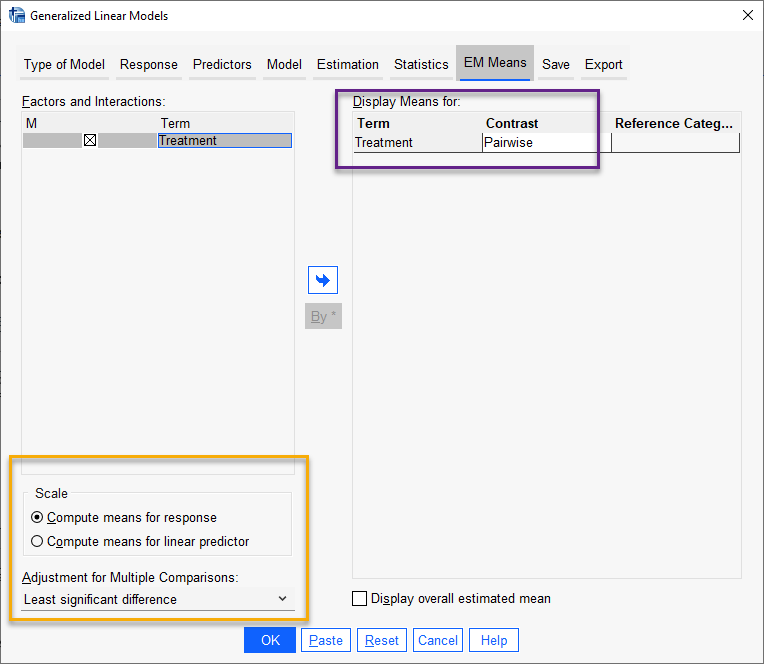
البته در این مثال اثر متقابل نداشته‌ایم. با این حال با انتخاب گزینه Pairwise می‌توانیم به مقایسه سطوح فاکتورهای مختلف با یکدیگر بپردازیم.

در پایین پنجره EM Means کادر دیگری با نام Scale دیده می‌شود. بر مبنای گزینه‌های این بخش می‌توانیم میانگین‌های حاشیه‌ای کمیت پاسخ را بر روی داده‌های اصلی Response و یا بر روی داده‌های تبدیل شده (بر مبنای تابع پیوند انتخاب شده)، به دست آورد.

بخش دیگر این پنجره که با نام Adjustment for Multiple Comparisons مشخص شده است، به تعدیل مقایسه‌های چندگانه می‌پردازد. این کار هنگامی انجام می‌شود که تعداد مقایسه‌های چندگانه متعددی داشته باشیم. با انجام این کار احتمال به دست آوردن نتایج معنادار بر مبنای شانس و تصادف کاهش می‌یابد و صرفاً مقایسه‌های کاملاً معنادار با مقادیر احتمال اندک، معنادار گزارش می‌شود.

در کادر بازشو این کادر می‌توانیم انواع روش‌های تعدیل را مشاهده کنیم. شاید معروفترین آن‌ها همان بونفرونی باشد. در این موضوع می‌توانید این لینک را ببینید.

 

در تب Save می‌توانیم یافته‌ها و اطلاعات بیشتری از نتایج تحلیل را در قالب فایل دیتا به دست بیاوریم. انتخاب هر کدام از گزینه‌های این پنجره سبب می‌شود یک ستون جدید به فایل دیتا اضافه شده و نتایج گزینه انتخاب شده در آن ستون قرار گیرد. این لینک را ببینید.

 

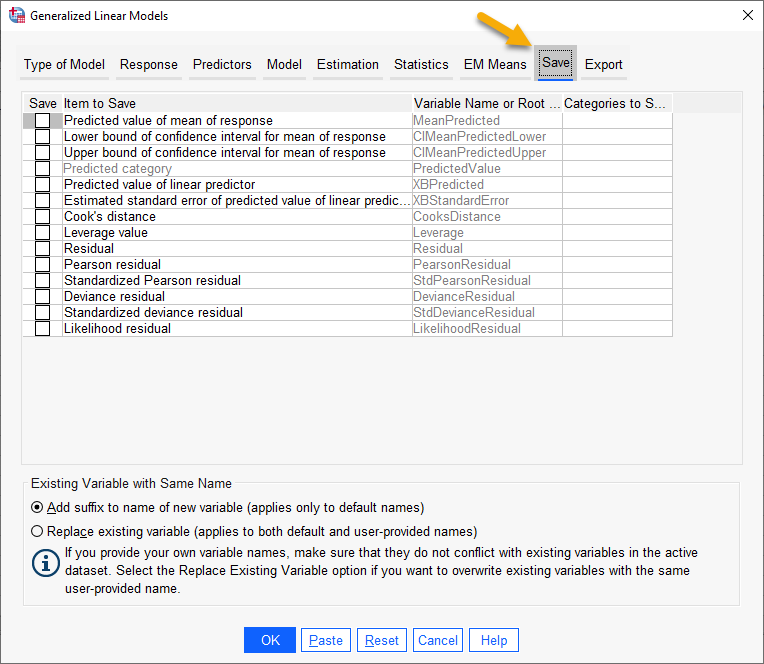
در نهایت تب Export در پنجره Generalized Linear Models دیده می‌شود. با استفاده از این تب می‌توانید خروجی‌ها و برخی از براورد پارامترهای مدل را در قالب یک فایل دیتا جدید، مشاهده کنیم. در این زمینه می‌توانید این لینک را ببینید.

 

نتایج تحلیل رگرسیون پواسن

 Poisson Regression Results 

در ابتدای نتایج و خروجی‌های نرم‌افزار SPSS جدول Model Information قرار دارد.

 

در این جدول بیان می‌شود که Dependent Variable مطالعه Number of Recurrences است. توزیع احتمال نیز به دلیل اینکه کمیت پاسخ به صورت شمارش و تعداد است، پواسن Poisson تعریف می‌شود. همچنین تابع پیوند ما لگاریتمی Probit است.

در جدول Categorical Variable Information اطلاعات توصیفی شامل تعداد و درصد به ازای هر کدام از گروه‌های فاکتور مطالعه یعنی Treatment (که نقش Independent Variable را دارد) به دست آمده است.

 

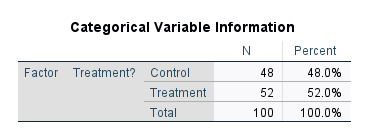
نتایج جدول بالا نشان می‌دهد 48 نفر در گروه کنترل و نفر 52 نیز در گروه درمان قرار دارند.

در جدول Continuous Variable Information آماره‌های توصیفی برای کمیت‌های پیوسته مطالعه یعنی تعداد عود، تعداد تومور و سایز بزرگترین تومور به دست آمده است.

 

جدول بالا نشان می‌دهد میانگین تعداد دفعات عود تومور 0.96 و انحراف معیار آن 1.348 است. بهترین چیزی که می‌توانید از این جدول بدست آورید این است که آیا ممکن است در تحلیل شما پراکندگی بیش از حد وجود داشته باشد (پیش‌فرض شماره 5 رگرسیون پواسون). می توانید این کار را با در نظر گرفتن نسبت واریانس (مربع ستون “Std. Deviation”) به میانگین (ستون “Mean”) برای کمیت وابسته انجام دهید. در مثال ما نتیجه زیر به دست می‌آید.

$ \displaystyle S{{d}^{2}}/M={{\left( {1.348} \right)}^{2}}/0.96=1.89$

عدد 1.89 به دست آمده (این نسبت در توزیع دقیق پواسن برابر با یک است) نشان می‌دهد قبل از اینکه X ها را اضافه کنیم، کمی بیش‌پراکندگی وجود دارد. با این حال، هنگامی که همه کمیت‌های مستقل به رگرسیون پواسون اضافه شدند، باید این فرض را بررسی کنیم.

در جدول Goodness of Fit نتایجی مبنی بر نیکویی برازش به دست آمده است.

 

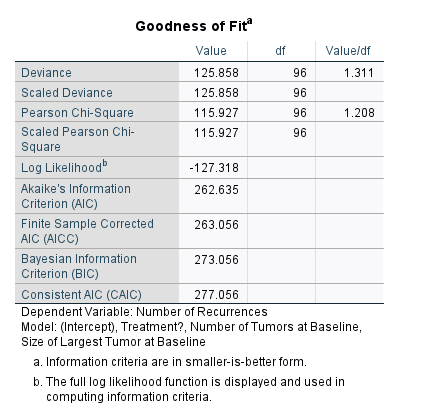
این جدول معیارهایی را ارایه می‌دهد که برای مقایسه با مدل‌های دیگر مفید است. در هر مدلی که شاخص‌هایی مانند AIC و BIC در آن کمتر باشد، می‌توان نتیجه گرفت آن مدل بهتر است. البته که ابزارهای تصمیم‌گیری دیگری نیز وجود دارد.

علاوه بر آن Value/df که بیانگر نسبت آماره آزمون بر درجه آزادی است، ابزار خوبی است که می‌تواند بیانگر مناسب بودن مدل برازش شده در نظر گرفته شود. این نسبت برای رگرسیون پواسون باید نزدیک به 1.0 باشد. یعنی یک نسبت معقولی بین درجه آزادی آزمون و آماره آزمون وجود داشته باشد.

خوب است این نکته را بدانید که درجه آزادی آزمون از رابطه‌ی زیر به دست می‌آید.

$\displaystyle df=n-\left( {\sum\limits_{{i=1}}^{p}{{\left( {{{k}_{i}}-1} \right)+1+Cov+MD}}} \right)$

در این رابطه، n تعداد نمونه، k تعداد سطوح و لول‌های هر فاکتور موجود در مدل، p تعداد فاکتورهای مطالعه، Cov تعداد کوریت‌های موجود در مدل و MD تعداد داده‌های گمشده است. به عنوان مثال ما در اینجا 100 نمونه داشته‌ایم. یک فاکتور با دو سطح (کنترل و درمان) و تعداد دو کوریت در مدل وجود دارد. داده گمشده نیز نداریم. بنابراین رابطه $ \displaystyle df=100-\left( {\left( {2-1} \right)+1+2+0} \right)=96$ وجود دارد.

در مثال ما نسبت Value/df برابر با 1.208 (بر مبنای آزمون پیرسن کای – اسکوئر) به دست آمده است. در این نسبت مقدار 1 نشان‌دهنده پراکندگی همسان است در حالی که مقادیر بیشتر از 1 نشان‌دهنده پراکندگی بیش از حد و اعداد کمتر از 1 بیانگر عدم پراکندگی است.

معمولاً در مثال‌ها و مطالعات رایج‌ترین نوع نقض فرض، همسانی پراکندگی بیش از حد است. یعنی مشاهده اعداد بزرگتر از 1. با این حال در این مثال، مقدار 1.208 بعید است که نقض جدی این فرض باشد و می‌پذیریم که داده‌ها دارای توزیع پواسن با پراکندگی همسان هستند.

جدول بالا فاقد آزمون آماری و در نتیجه مقدار احتمال است که نرم‌افزار SPSS در ستونی با نام Sig نشان می‌دهد. در عوض جدول بعدی نتایج با نام Omnibus Test دارای آزمون آماری است. آن را ببینید.

 

در این جدول مدل برازش شده (در اینجا رگرسیون پواسن) با مدل فقط شامل ضریب ثابت (یعنی بدون هیچ‌کدام از Xها) مقایسه و آزمون شده است. نتیجه Omnibus Test نشان می‌دهد، مدل رگرسیونی برازش شده معنادار است. مفهوم این جمله این است که حداقل یکی از Xها دارای تاثیر معنادار بر کمیت پاسخ تعداد عود تومور است.

اکنون که می‌دانید اضافه کردن همه کمیت‌های مستقل یک مدل پواسن از نظر آماری معنی‌دار ایجاد می‌کند، می‌خواهید بدانید که کدام X ها از نظر آماری معنادار هستند. در بخش بعدی به این موضوع پرداخته می‌شود.

در جدول بعدی با نام Tests of Model Effects تاثیر هر کدام از X ها به صورت جداگانه بر روی Y (تعداد عود) آزمون شده‌اند. آن را ببینید.

 

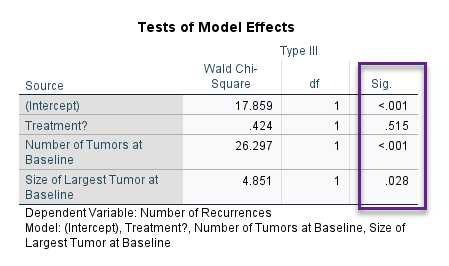
نتایج جدول بالا نشان می‌دهد درمان تاثیر معنادار بر Y ندارد (P-value=0.515). با این حال تعداد تومور (P-value<0.001) و اندازه بزرگترین تومور (P-value=0.028) دارای تاثیر معنادار بر تعداد عود می‌باشد.

جدول بعدی با نام Parameter Estimates در ادامه آمده است. تصویر آن را بینید.

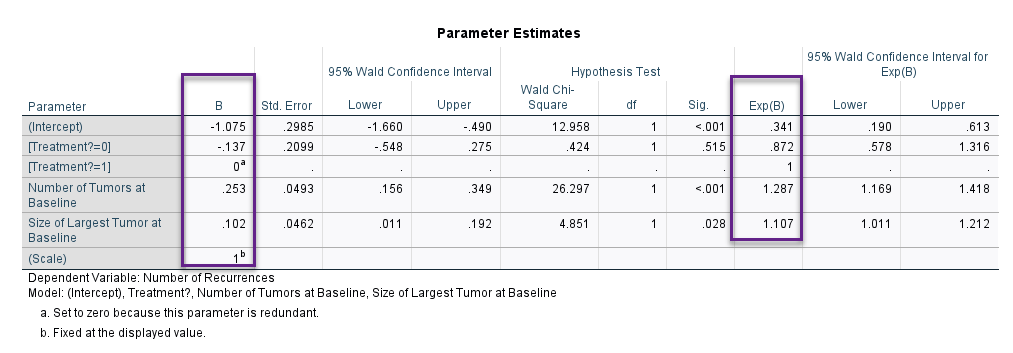
مثبت بودن ضریب رگرسیونی Size (B=0.102)، بیانگر آن است که افزایش سایز تومور، به افزایش احتمال پیشامد (عود تومور) منجر می‌شود. این نتیجه معنادار به دست می‌آید (P-value = 0.028). مقدار عددی شانس رخداد که به صورت 1.107 = Exp(B) نمایش داده می‌شود، نشان می‌دهد افزایش هر واحد سایز تومور، شانس عود تومور را حدود 1.11 برابر افزایش می‌دهد.

یافته دیگر این است که تعداد تومور نیز تاثیر معنادار و قوی بر عود تومور، در افراد مورد بررسی دارد (B=0.253, P-value < 0.001). در این‌جا نیز مقدار عددی شانس رخداد 1.287 = Exp(B) به دست آمده است. این عدد نشان می‌دهد افزایش هر واحد تعداد تومور، شانس عود تومور را حدود 1.29 برابر افزایش می‌دهد.

با این حال و همان‌گونه که قبلاً نیز گفتیم، درمان فاقد تاثیر معنادار بر عود است. هر چند ضریب رگرسیونی آن برای گروه کنترل منفی به دست آمده است (B=-0.137) و نشان می‌دهد افراد گروه کنترل شانس عود کمتری نسبت به افراد گروه درمان دارند، با این حال این یافته معنادار نیست (P-value = 0.515).

در ادامه خروجی‌های نرم‌افزار SPSS، نتایج با نام Estimated Marginal Means: Treatment? دیده می‌شود.

 

در این جدول میانگین‌های حاشیه‌ای تعداد عود تومور به ازای هر کدام از گروه‌های کنترل و درمان آمده است. خطای استاندارد و فواصل اطمینان 95 درصد نیز براورد شده است. نتایج این جدول به وضوح نشان می‌دهد میانگین عود تومور در گروه کنترل در مقایسه با گروه درمان کمتر است. این همان نتیجه‌ای بود که ما در جدول Parameter Estimates به آن رسیده بودیم. یعنی منفی بودن ضریب رگرسیون پواسن گروه کنترل نسبت به گروه درمان.

از دیگر نتایج این بخش جدول Pairwise Comparisons می‌باشد. در این جدول به مقایسه دو به دو گروه‌های فاکتور درمان، با یکدیگر مقایسه شده است.

 

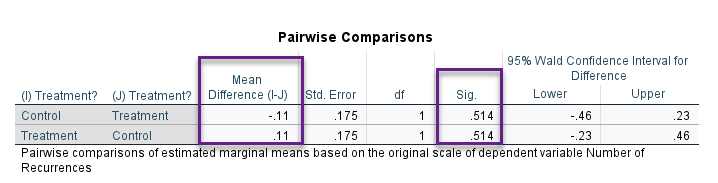
فاکتور درمان فقط دارای دو گروه بوده است. چنانچه فاکتورهای دیگری نیز در این مطالعه وجود داشت می‌توانستیم نتایج این جدول را بهتر و با یافته‌های بیشتر ببینیم.

در نهایت نیز در خروجی نرم‌افزار جدول با نام Overall Test Results آمده است.

 

در این جدول می‌توانید نتیجه آزمون کلی همه‌ی مقایسه‌های دو به دو جدول Pairwise Comparisons را مشاهده کنید. مقدار احتمال به دست آمده در این جدول همان عدد جدول Pairwise Comparisons می‌باشد. دلیل این مطلب آن است که در جدول مقایسه‌های دو به دو، فقط دو گروه کنترل و درمان وجود داشته است. بنابراین نتایج جدول Pairwise Comparisons با جدول Overall Test Results مشابه خواهد بود.

 

 

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2022). Poisson regression model in SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/poisson-regression-spss/.php

For example, if you viewed this guide on 12^th January 2022, you would use the following reference

GraphPad Statistics (2022). Poisson regression model in SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/poisson-regression-spss/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.