ضریب همبستگی درون رده ای Intraclass Correlation Coefficient (ICC)
توضیحات تحلیل پایایی برگرفته شده از کتاب روش های پیشرفته آماری و کاربردهای آن- انتشارات جامعهنگر
پایایی Reliability یک پرسشنامه به معنای آن است که ابزار اندازهگیری تا چه اندازه نتایج یکسانی به دست میدهد. یعنی اگر پرسشنامه را در یک فاصله زمانی، چندین بار به گروه یکسانی بدهیم، نتایج حاصل تا چه اندازه میتواند مشابه باشد.
هر چند این موضوع پذیرفته شده است که نمیتوان انتظار داشت این نتایج به طور کامل یکسان باشد چرا که آزمودنی ما غالباً انسان است که در شرایط محیطی و ذهنی گوناگون میتواند به یک پرسش، پاسخهای نهچندان یکسانی دهد. پایایی یک اندازه عددی قابل سنجش است.
چرا از همبستگی درون ردهای استفاده میکنیم؟
در این لینک درباره پایایی بین ارزیابان یا همان Interrater Reliability توضیح دادیم و بیان کردیم که بهترین روش به منظور به دست آوردن این نوع پایایی، مفهومی به اسم ضریب همبستگی درون رده ای Intraclass Correlation Coefficient یا به صورت مخفف ICC است.
در این نوشتار قصد داریم درباره ICC و روشها و مدلهای مختلف به دست آوردن آن صحبت کنیم.
خاطرتان باشد در همان متن Interrater Reliability بیان کردیم هنگامی که بخواهیم میزان توافق و پایایی بین دو ارزیاب را به دست بیاوریم به سادگی میتوانیم از ضریب کاپا استفاده کنیم. حال اگر تعداد ارزیابها بیشتر از دو نفر باشد، استفاده از ICC ها کاربرد پیدا میکند.
در ابتدا و جهت توضیح ضریب همبستگی درون رده ای بیایید از یک مثال شروع کنیم. پس از آن میتوان با فهم و درک بهتری درباره انواع مختلف مدلهای ICC صحبت کرد.
مثال ضریب همبستگی درون رده ای (ICC)
کمیته بین المللی المپیک در پاسخ به انتقادات رسانهای، در پی بررسی نمرات و امتیازات داده شده توسط داوران آموزش دیده این کمیته است. در این بررسی میخواهیم میزان پایایی و قابل اعتماد بودن نمرات اختصاص داده شده را اندازهگیری کنیم. فایل این مثال را میتوانید با نام ICC.sav از اینجا دریافت کنید.
این مثال مربوط به امتیازات داده شده توسط هشت داور به 300 اجرای ژیمناستیک است. هر سطر نشاندهنده عملکرد و اجرای یک نفر است. داوران از اجراهای یکسانی دیدن کردهاند و هر داور به صورت جداگانه به هر کدام از 300 اجرا، امتیاز داده است.
از آنجا که تعداد داوران و یا همان ارزیابان بیشتر از دو نفر است، میتوانیم از پایایی نوع Interrater و ضریب همبستگی درون رده ای یا همان ICC استفاده کنیم.
خوب است این نکته را بدانید که ICC یک روش ار نوع آنالیز واریانس ANOVA است که در آن پاسخها (Responses) همان نمرات اختصاص داده شده توسط ارزیابان و داوران است.
نکته نکته با اهمیت دیگری که در این میان مهم است و در آینده و بیان توضیحات بیشتر درباره ICC، مورد توجه ما قرار خواهد گرفت، مفهومی به نام منابع تنوع Sources of Variation است. برای درک این مفهوم به مثال بالا برگردیم.ساختار مثال بالا شامل بخشهای زیر است.
الف) 300 نفری که به آنها امتیاز و نمره داده شده است.
ب) هشت داوری که به هر فرد، نمره و امتیاز دادهاند.
این بخشها هر کدام میتوانند به صورت تصادفی از یک مجموعه بزرگتر انتخاب شده باشند. یعنی هم ۳۰۰ نفر اجرا کنندگان میتوانند از بین تعداد زیاد شرکتکنندگان به تصادف انتخاب شده باشند و هم هشت نفر داوران میتوانند از یک مجموعه بزرگتر داوران، به صورت تصادفی انتخاب شده باشد.
ما میتوانیم این مثال را یک طرح و مدل تصادفی دو طرفه یعنی Two-way Random بدانیم، که هر دو جزء آن یعنی اجراکنندگان (کسانی که به آنها امتیاز و نمره داده میشود) و داوران (کسانی که نمره و امتیاز میدهند) به صورت تصادفی از یک مجموعه بزرگتر انتخاب میشوند.
یک حالت دیگر را نیز میتوانیم فرض کنیم. در این حالت، ارزیابان و داوران امتیاز دهنده، ثابت و یکتا بوده و بخشی از یک مجموعه بزرگتر داوران نیستند. این مدل و طرح را آمیخته دو طرفه یا Two-way Mixed مینامیم.
بیایید یک حالت انتزاعی دیگر را نیز درنظر بگیرید. گفتیم که هر داور به ۳۰۰ نفر اجراکننده یکسان، نمره میدهد. حال اگر هر داور به افراد متفاوت و اجراکنندگان مختلفی امتیاز بدهد، ما این طرح را یک طرفه تصادفی One-way Random نامگزاری میکنیم. در این حالت نمیدانیم هر نمره توسط کدام داور، داده شده است.
بنابراین ما در یک مطالعه از نوع پایایی Inter-Rater با سه مدل Two-way Random یا Two-way Mixed و در برخی موارد One-way Random روبهرو هستیم. سعی میکنیم در ادامه درباره آنها بیشتر حرف بزنیم.
نوع خوب است در اینجا به دو نوع ضریب همبستگی درون ردهای یا همان ICC، نیز اشاره کنیم. این دو نوع عبارتند از ثبات Consistency و توافق مطلق Absolute Agreement.
در واقع علاوه بر اینکه ما با سه مدل جهت به دست آوردن مقدار ICC روبهرو هستیم، دو روش محاسباتی یعنی Consistency و Absolute Agreement نیز وجود دارد.
به منظور درک این مطلب که این دو نوع روش محاسباتی چه هستند و هر کدام در چه مواردی استفاده میشوند، بیایید بر روی بخش ب در ساختار بالا یعنی هشت داور و ارزیاب، تمرکز کنیم.
ببینید، وقتی ما با چند ارزیاب روبهرو هستیم، دو نوع پراکندگی و واریانس داریم. یک واریانس بین ارزیابان و اصطلاحاَ inter-observer و دیگری واریانس درون ارزیابان یا اصطلاحاَ intra-observer.
در واریانس بین ارزیابان، پراکندگی و تنوع بین داوران و امتیازدهندگان، به دست میآید و در واریانس درون ارزیابان، پراکندگی نحوه امتیازدهی یک داور در بین نمرات خودش به دست میآید.
حال میتوان درباره انواع روشهای محاسباتی ICC توضیح داد.
توضیح اینکه ICC از نوع Consistency هنگامی استفاده میشود که واریانس و اختلاف بین ارزیابان برای ما اهمیت چندانی نداشته باشد و در واقع نمیخواهیم آن را در مطالعه خود در نظر بگیریم. در این روش فقط واریانس درون ارزیابان در محاسبه ICC استفاده میشود.
اما ICC از نوع Absolute Agreement هنگامی استفاده میشود که واریانس بین ارزیابان نیز برای ما اهمیت داشته باشد. در این روش علاوه بر واریانس درون ارزیابان در محاسبه ICC از واریانس بین ارزیابان هم استفاده میشود.
اینکه از کدام روش یعنی Consistency یا Absolute Agreement استفاده کنیم، یک موضوع آماری نیست و به همان مطالعه، نحوه جمعآوری دادهها و سوالات تحقیق مربوط میشود.
در همان مثال کمیته بین المللی المپیک اگر داوران بر مبنای الگوهای مشابهی امتیازدهی کنند، بنابراین واریانس بین داوران چندان اهمیتی ندارد و استفاده از روش Consistency نسبت به روش Absolute Agreement معتبرتر است.
حال اگر مقررات IOC سختگیرانهتر باشد و هر داور بر مبنای ایده و الگوهای منحصربه فرد خود امتیاز دهد، در این صورت واریانس بین ارزیابان برای ما دارای اهمیت است و استفاده از زوش Absolute Agreement نسبت به روش Consistency معتبرتر است.
حال در ادامه و با بیان این توضیحات، به ادامه مثال و انجام تحلیل پایایی با استفاده از نرمافزار SPSS جهت به دست آوردن اندازه توافق بین هشت داور، میپردازیم. سعی میکنیم توضیحات بیشتر درباره تحلیل پایایی از نوع Inter-Rater و یافتن ICC را پس از مثال پی بگیریم.
استفاده از نرمافزار SPSS جهت محاسبه ICC
در ابتدای کار میخواهیم اندازهی پایایی این مثال با استفاده از ضریب همبسنگی درون ردهای را بسنجیم. به منظور به دست آوردن ضرایب مختلف قابلیت اعتماد و یا همان پایایی از مسیر زیر در نرمافزار SPSS استفاده میکنیم.
Analyze → Scale → Reliability Analysis

در پنجره باز شده با نام Reliability Analysis ستونهای مربوط به نمرات هر داور را در کادر Items قرار میدهیم.
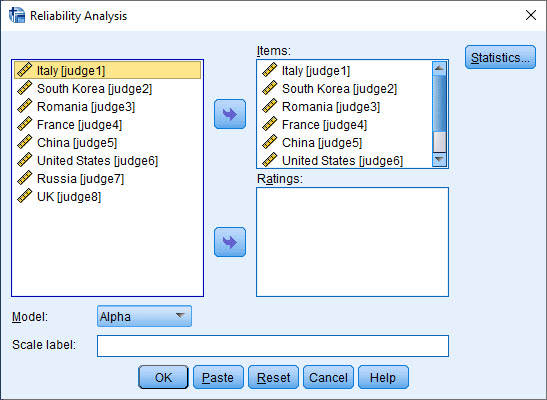
سپس دکمه Statistics را میزنیم. پنجره زیر برای ما باز میشود.
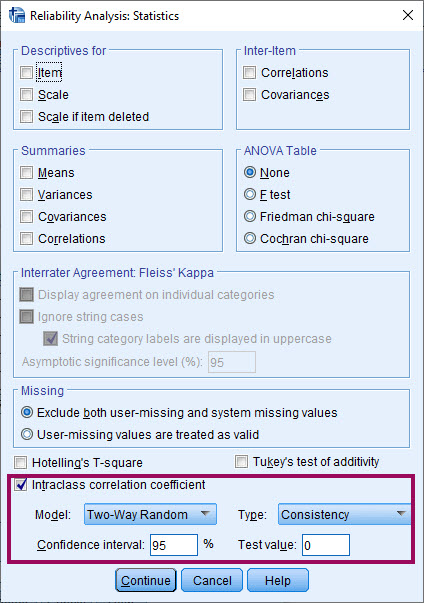
درباره گزینههای مختلف و کادرهای این پنجره در این لینک توضیح دادیم. در این متن میخواهیم دربارهی کادر Intraclass Correlation Coefficient صحبت کنیم. این کادر دارای دو منو یکی با نام Model و دیگری با نام Type است.
در منوی Model سه گزینه وجود دارد. آنها عبارتند از Two-Way Mixed، Two-Way Random و One-Way Random. درباره این گزینهها در بخشهای قبل توضیح دادیم.

همچنین در منوی Type نیز گزینههای Consistency و Absolute Agreement دیده میشود. درباره این گزینهها نیز قبلاَ صحبت کردیم.
سوال حتماَ این سوال پیش میآید در این مثال از کدام گزینهها استفاده کنیم. بیایید یکبار دیگر مثال را مرور کنیم.
ما ۳۰۰ نفر اجراکننده داشتیم که از یک مجموعه اجراکنندگان بزرگتر به تصادف انتخاب شده است. همچنین هشت داور و ارزیاب نیز داریم که میتوانیم فرض کنیم آنها نیز از مجموعه داوران بزرگتر، به صورت تصادفی انتخاب شدهاند. بنابراین مدل ما Two-Way Random خواهد بود.
از طرف دیگر فرض کنید داوران بر مبنای الگوهای مشابهی امتیازدهی کنند، یعنی مثلاَ در مقابل آنها فرم یکسانی است و آنها بر مبنای همان فرم و آیتمهای قرار گرفته در فرم، به اجراکنندگان نمره میدهند. بنابراین نوع Type ما در این مثال Consistency خواهد بود. به عنوان مثال در جلسه دفاع از پایاننامه، داوران نیز دارای فرمهای ارزشیابی یکسانی هستند، در این موارد نیز نوع پایایی ICC همان Consistency میباشد.
دو گزینه دیگر در کادر Intraclass Correlation Coefficient دیده میشود. یکی از این گزینهها عبارت است از Confidence Interval که به صورت پیشفرض بر روی ۹۵٪ قرار گرفته است. با استفاده از این گزینه، فواصل اطمینان ۹۵ درصد برای ضریب همبستگی درون رده ای نیز به دست میآید.
گزینه دیگری نیز با نام Test value مشاهده میشود. این گزینه نیز خروجی مفیدی دارد. ببینید هر کجا آزمون Test است، فرضیههای آماری نیز وجود دارند و در نتیجه مقدار احتمال P value هم به دست میآید. سوال مهم در اینجا این است فرضیههای آماری ICC چه هستند که قرار است، روی آنها آزمون انجام شود. من در ادامه فرضهای صفر و مقابل را نوشتهام.
H0 : ICC = a0 vs H1 : ICC > a0
به معنای اینکه در فرض صفر آزمون میکنیم، آیا ICC براورد شده برابر با مقدار ثابت a0 است و در فرض مقابل آزمون میکنیم آیا ICC از مقدار ثابت a0 بزرگتر است.
به صورت پیشفرض نرم افزار SPSS عدد a0 را برابر با صفر در نظر میگیرد. بنابراین فرضیههای آماری بالا به صورت زیر، در میآیند.
H0 : ICC = 0 vs H1 : ICC > 0
به معنای آنکه آزمون میکنیم، آیا ICC براورد شده برابر صفر است و یا از عدد صفر بزرگتر است. اگر فرض صفر پذیرفته شود، به معنای این است که داوران و ارزیابان هیچگونه توافقی با هم ندارند و پایایی مطالعه غیرقابل قبول است، اگر هم فرض مقابل تایید شود، میتوان درباره پایایی مطالعه صحبت کرد.
نکته مهمی که در اینجا وجود دارد این است که عدد صفر کادر Test value بالا را میتوان به دلخواه عوض کرد. اصولاَ فرضیه ICC برابر با صفر بودن به شدت بدبینانه و غیرمنطقی است و حداقل اندازه ICC باید بالای ۰.۵ باشد، تا بتوان درباره پایایی مطالعه، اظهارنظر کرد. بنابراین حتی بهتر است در کادر بالا به جای صفر عدد ۰.۵ را قرار دهیم.
به هر حال، ما فعلاَ همان عدد پیشفرض نرمافزار SPSS را قرار دادهایم و نتایج را بر مبنای همان پی میگیریم.
خوب است علاوه بر محاسبه ICC، آمارههای توصیفی نمرات داده شده هر داور را نیز بدانیم. برای این منظور میتوانیم در کادر Descriptives for گزینه Item را انتخاب کنیم. تصویر زیر را ببینید.

حال Continue کرده و سپس OK میکنیم. در پنجره Output نرمافزار SPSS میتوانیم خروجیها و نتایج به دست آمده را مشاهده کنیم.
نتایج تحلیل پایایی پرسشنامه
در ابتدا برنامه و Syntax های این تحلیل را مشاهده میکنید. استفاده از Syntax ها و محیط برنامه نویسی SPSS کاملاَ توصیه می شود.
RELIABILITY
/VARIABLES=judge1 judge2 judge3 judge4 judge5 judge6 judge7 judge8
/SCALE('ALL VARIABLES') ALL
/MODEL=ALPHA
/STATISTICS=DESCRIPTIVE
/ICC=MODEL(RANDOM) TYPE(CONSISTENCY) CIN=95 TESTVAL=0
با استفاده از همین چند خط فرمان در محیط Syntax نرم افزار SPSS میتوانیم به سادگی، تحلیل پایایی، ضریب آلفا کرونباخ، ضریب همبستگی درون ردهای ICC و جداول و آمارههای مربوطه را به دست بیاوریم. حال به ترتیب به بیان نتایج به دست آمده میپردازیم.
-
جدول Case Processing Summary
در خروجیهای نرمافزار، ابتدا جدول زیر با نام Case Processing Summary مشاهده می شود.

در این جدول تعداد سطرها و یا همان افراد مورد بررسی، آمده است. مشاهدات بر مبنای تعداد افراد واقعی و تعداد افراد نادیده گرفته شده Excluded تقسیم شده است. در این مثال ۳۰۰ نفر اجراکننده وجود داشته است که هیچکدام Missing نبودهاند و همگی در تحلیل قرار گرفتهاند.
-
جدول Reliability Statistics
جدول Reliability Statistics را میتوان یکی از مهمترین یافتههای تحلیل پایایی دانست. نتایج این جدول در ادامه آمده است.
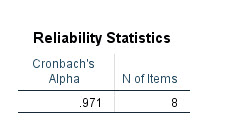
در ستون Cronbach’s Alpha عدد ضریب آلفای کرونباخ به دست آمده است. اندازه آن برابر با 0.971 شده است، این اندازه بیانگر پایایی خوب و عالی دادهها در این مطالعه میباشد. چنانچه در زمینه آلفا کرونباخ به توضیحات بیشتری علاقمند هستید، میتوانید این لینک را ببینید.
ستون دیگر با نام N of items به سادگی به تعداد آیتمها (در این مثال تعداد ارزیابها) قرار گرفته در تحلیل پایایی اشاره دارد. در این مثال چون پایایی را بر روی هشت داور به دست آوردهایم، بنابراین N of items برابر با 8 شده است.
-
جدول Item Statistics
فهم جدول Item Statistics بسیار ساده است.
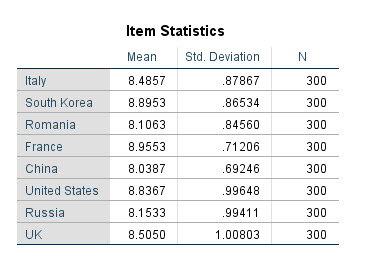
همانگونه که میبینید به ازای هر کدام از داوران (هشت داور)، آمارههای توصیفی شامل میانگین، انحراف معیار و تعداد افراد اجرا کننده، آمده است. ستون N که به ازای هر داور برابر با ۳۰۰ شده است، به سادگی نشان میدهد داوران به اجراکنندگان یکسانی، امتیاز و نمره دادهاند.
به عنوان مثال برای داوری از کشور ایتالیا، میانگین نمرات داده شده به ۳۰۰ نفر اجراکننده، برابر با ۸.۴۸۶ و انحراف معیار آنها ۰.۸۷۹ شده است.
همچنین داور اهل کشور چین، کمترین میانگین نمرات را به افراد داده است (۸.۰۳۹). به نظر میرسد این داور نسبت به بقیه سختگیرتر است. با این حال داور اهل فرانسه بیشترین میانگین نمرات را به افراد اجراکننده داده است (۸.۹۵۵). بالا بودن انحراف معیار در داوران آمریکا، روسیه و انگلیس بیانگر نمرات پراکنده آنها نسبت به سایر داوران است.
حال به موضوع اصلی این مطالعه که همان جدول Intraclass Correlation Coefficient است، میپردازیم. در ادامه میتوانید توضیحات درباره نتایج این جدول را مشاهده کنید.
-
جدول Intraclass Correlation Coefficient
جدول Intraclass Correlation Coefficient همانگونه که دیده میشود، در دو سطر یکی با نام Single Measures و دیگری Average Measures آمده است.
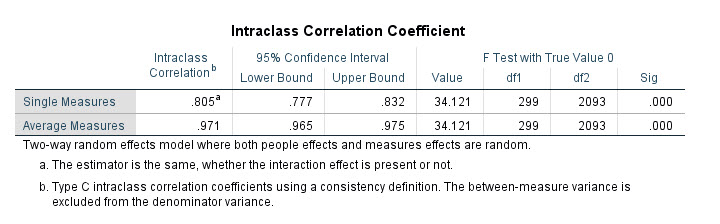
سطر Single Measures و نتایج به دست آمده بر مبنای آن، مربوط به حالتی است که فرض کنیم، تنها یک ابزار قضاوت و منبع تصمیمگیری یا ارزیاب وجود دارد. در واقع حتی اگر بیش از یک ارزیابی در آزمایش انجام شده باشد، پایایی ICC برای حالتی به دست میآید که در آن یک اندازهگیری واحد از یک ارزیاب انجام میشود.
به همین ترتیب سطر Average Measures مربوط به حالتی است که پایایی ICC برای میانگین ارزیابان و داوران محاسبه میشود.
حال بیایید به بیان بخشها و ستونهای مختلف جدول Intraclass Correlation Coefficient بپردازیم.
Intraclass Correlation
ستون Intraclass Correlation و اعداد آن، همان چیزی است که به دنبال آن هستیم. عدد ۰.۸۰۵ بیانگر مقدار ضریب همبستگی درون ردهای یا همان ICC در سطر Single Measures برای حالتی است که اندازهگیریها فقط توسط یک داور انجام میشود.
مقدار ICC در سطر Average Measures به خوبی بالا است. عدد ۰.۹۷۱ نشان میدهد، پایایی نمرات داده شده توسط داوران، هنگامی که میانگین آنها مورد بررسی قرار میگیرد، کاملاَ قابل قبول است.

95% Confidence Interval
ستون 95% Confidence Interval به سادگی فواصل اطمینان برای Intraclass Correlation را به دست داده است.
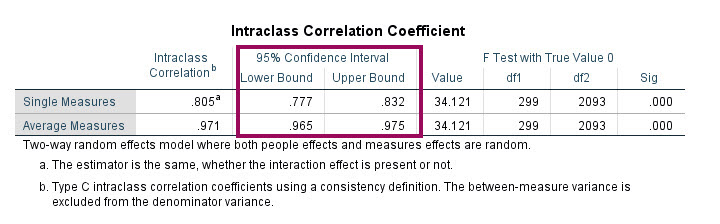
همانگونه که مشاهده می کنید برای Average Measures کران بالای فاصله اطمینان ICC عدد ۰.۹۷۵ شده است. این عدد بالا، بیانگر توافق بسیار خوب داوران با یکدیگر به حساب میآید.
F Test with True Value 0
خاطرتان باشد، به هنگام بیان تنظیمات تحلیل ICC و گزینه Test value بیان کردیم که نرم افزار SPSS به بررسی فرضیه آماری زیر به صورت پیشفرض میپردازد. البته در همان تنظیمات این امکان برای ما وجود داشت که عدد صفر پیشفرض را بر روی عدد دیگری قرار دهیم.
H0 : ICC = 0 vs H1 : ICC > 0
گفتیم که این فرضیه به معنای آن است که، آیا ICC براورد شده برابر صفر است و یا از عدد صفر بزرگتر است. اگر فرض صفر پذیرفته شود، یعنی داوران و ارزیابان هیچگونه توافقی با هم ندارند و پایایی مطالعه غیرقابل قبول است، اگر هم فرض مقابل تایید شود، میتوان درباره پایایی مطالعه صحبت کرد.
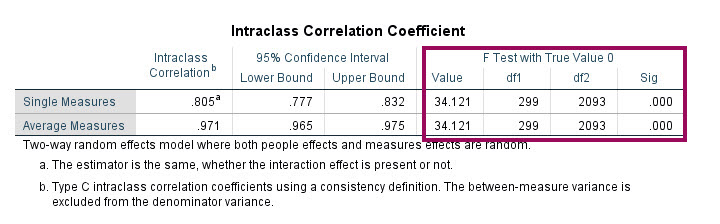
این فرضیه با استفاده از آزمون F انجام میشود. حال نتیجه به دست آمده در ستون F Test with True Value را ببینید. به این نکته توجه کنید که نتایج به دست آمده هم برای Single Measures و هم برای Average Measures یکسان است.
در ستون Value آماره آزمون F آمده است. میدانیم که آماره F دارای دو درجه آزادی است. درجه آزادی df1 در تحلیل ICC به صورت n-1 یعنی تعداد نمونه منهای یک به دست میآید. از آنجا که ۳۰۰ نمونه داریم پس df1 برابر با ۲۹۹ به دست آمده است.
همچنین df2 از رابطه (k-1)*(n-1) به دست میآید. k نیز همان تعداد ارزیابان و داوران است. پس df2 به سادگی از رابطه 2093 = (1-8)*(1-300) به دست آمده است.
در هر فرضیه و آزمون آماری نیز میدانیم که با مقدار احتمال و Sig روبهرو هستیم. عدد به دست آمده یعنی 0.001> نشان میدهد فرض صفر بالا یعنی برابر صفر بودن ICC رد میشود. بنابراین میپذیریم که به صورت معنادار ICC از عدد صفر بزرگتر است. همانگونه که قبلتر نیز گفتم، به سادگی میتوانیم در تنظیمات نرمافزار به جای عدد صفر در Test value عدد بزرگتر دیگری قرار دهیم.
نکته خوب است این نکته را بدانیم که اندازهها و عددهای به دست آمده برای پایایی ICC چه از مدل Two-Way Random برویم و یا از مدل Two-Way Mixed یکسان است. بلکه تفاوت در تفسیر نتایج است.
یادتان باشد گفتیم از مدل Two-Way Mixed هنگامی استفاده میکنیم که ارزیابان و داوران امتیاز دهنده، ثابت و یکتا بوده و بخشی از یک مجموعه بزرگتر داوران نیستند. بنابراین خیلی ساده، نتایجی که بر مینای مدل Two-Way Mixed به دست میآید قابل تعمیم و گسترش به سایر داوران و ارزیابان نیست.
اما در یک مدل تصادفی دو طرفه یعنی Two-way Random گفتیم که هر دو جزء آن یعنی اجراکنندگان و داوران به صورت تصادفی از یک مجموعه بزرگتر انتخاب میشوند، بنابراین نتایجی که بر مبنای مدل Two-way Random به دست میآیند، قابل تعمیم و گسترش به سایر ارزیابان هستند.
مهم الف) از ضریب همبستگی درون رده ای یا همان ICC هنگامی که یک فرد یا منبع تصمیمگیری، چندین مرتبه و در زمانهای مختلف، به یک مفهوم واحد، اندازههای عددی اختصاص میدهد، نیز به کار میرود. به عنوان مثال در یک مطالعه با زمانهای اندازهگیری قبل، بعد و پیگیری که در پی بررسی تاثیر مداخله آموزشی هستیم، میخواهیم پایایی و همبستگی درونی بین زمانها را به دست بیاوریم. در این حالت میتوانیم از تحلیل ICC استفاده کنیم. معمولاَ در این مثالها، نوع ICC ما Consistency خواهد بود. به همین ترتیب از آنجا که زمانها، تصادفی نیستند و بلکه از قبل تعیین شده و Fix هستند، مدل تحلیل ICC ما نیز به صورت Two-way Mixed میباشد.
ب) هنگامی که مطالعه ما One-way Random است، یعنی داوران و ارزیابان هر یک به اجراکنندگان و افراد متفاوتی امتیازدهی کردهاند، انتخاب Type یعنی Consistency یا Absolute Agreement تحلیل ICC به دلیل اینکه واریانس بین ارزیابان حاصل محاسبه بین افراد و اجراکنندگان یکسانی نیست، معنایی ندارد. به همین دلیل است که با انتحاب مدل One-way Random در نرمافزار SPSS، گزینههای Type غیرفعال میشوند.
دلیل دیگری که برای غیر فعال بودن Consistency در مدل One-way Random مطرح میشود این است که ما از Consistency هنگامی استفاده میکنیم که مطالعه ما دارای زمان و تایمهای مختلف اندازهگیری است. یعنی یک مفهوم و یا همان Subject را در چند تایم مختلف اندازهگیری میکنیم و میخواهیم پایایی بین این زمانها را یا یکدیگر به دست بیاوریم. واضح است که در این مدل نمیتوانیم از One-way Random استفاده کنیم، زیرا در هر زمان همه Subjectها را اندازه میگیریم و اینگونه نیست که در یک تایم، برخی از موارد و در تایم دیگر موارد دیگری را اندازهگیری کنیم.
به این نکته هم توجه کنید که چنانچه در یک مطالعه، استفاده از آرا و نظرات افراد یکسان منع شده باشد و هر فرد باید به یک موضوع رای دهد، استفاده از مدل one-way random effects توصیه میشود.
سوال حتماَ این سوال برای شما مطرح میشود که اندازه عددی ICC چقدر باشد، خوب است؟
پاسخ این است که ما معمولاَ به اندازههای ICC کمتر از ۰.۵ اهمیت نمیدهیم و آنها را پایایی ضعیف مینامیم. مقادیر ICC بین ۰.۵ و ۰.۷۵ پایایی متوسط و بین ۰.۷۵ تا ۰.۹ پایایی خوب نامیده میشود. برای اندازههای بالاتر از ۰.۹ نیز میگوییم پایایی ما عالی است.
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2021). Intraclass Correlation Coefficient using SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/intraclass-correlation-coefficient/.php
For example, if you viewed this guide on 12th January 2022, you would use the following reference
GraphPad Statistics (2021). Intraclass Correlation Coefficient using SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/intraclass-correlation-coefficient/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.

