باقیمانده ها Residuals در رگرسیون خطرات متناسب کاکس

 Residuals 

جهت فهم بهتر مطلب پیشنهاد می‌کنم ابتدا مقاله (رگرسیون خطرات متناسب کاکس Cox Proportional Hazards Regression چیست؟) را مطالعه کنید.

در تب Residuals انتخاب کنید که نرم‌افزار کدام باقیمانده‌ها را گزارش و نمودار آن‌ها را رسم کند. این نتایج بینشی در مورد کیفیت و مناسب بودن برازش مدل ایجاد شده، ارایه می‌کند و همچنین برخی از مفروضات رگرسیون را ارزیابی می‌کند.

توجه داشته باشید که “Residuals” رگرسیون خطرات متناسب کاکس از نظر ریاضی با باقیمانده‌های رگرسیون خطی متفاوت است. با این حال، آن‌ها را می‌توان جهت پاسخ به سوالات و آزمون فرضیات مشابه که در همه‌ی مدل‌های رگرسیونی استفاده می‌شود، به کار برد.

این نکته مهم است که مقادیری که در رگرسیون کاکس به عنوان باقیمانده ذکر می‌شود، به معنای کلاسیک باقیمانده نیستند. همان‌گونه که می‌دانیم در رگرسیون خطی چندگانه (و همچنین رگرسیون خطی ساده و رگرسیون غیرخطی)، باقیمانده به عنوان تفاوت بین مقدار مشاهده شده و مقدار پیش‌بینی‌شده $\displaystyle \left( {{{e}_{i}}={{y}_{i}}-{{{\hat{y}}}_{i}}} \right)$ تعریف می‌شود.

به عنوان مثال، اگر مدل رگرسیون خطی چندگانه برای براورد قد یک فرد با استفاده از کمیت‌های سن، جنسیت و وزن ایجاد شود، می‌توانید هر یک از قدهای اندازه‌گیری شده مورد استفاده برای ساخت مدل و قدهای مربوطه را که توسط مدل پیش‌بینی شده است، با یکدیگر مقایسه کنید. با استفاده از مقادیر ورودی یکسان سن، جنسیت و وزن. تفاوت بین این دو مقدار (مشاهده و پیش بینی شده) باقیمانده Residual خواهد بود.

متاسفانه، درک مستقیمی از این مفهوم “منهای مشاهده شده واقعی” برای رگرسیون خطرات متناسب کاکس وجود ندارد. به جای آن، تعدادی مقادیر مختلف پیشنهاد شده‌اند که تلاش می‌کنند به سوالات مشابهی در رگرسیون خطرات متناسب کاکس همانند باقیمانده‌های استاندارد برای در دیگر انواع رگرسیون (مانند رگرسیون خطی چندگانه) پاسخ می‌دهند.

در تصویر زیر می‌توانید تب Residuals در تنظیمات رگرسیون خطرات متناسب کاکس را مشاهده کنید.

 

من پنجره Residuals بالا را شماره‌گزاری کرده‌ام. در ادامه به ترتیب به توضیح آن‌ها می‌پردازم.

در این بخش به موضوع معتبر بودن فرض خطرات متناسب پرداخته شده است. در اینجا این سوال پرسیده می‌شود که آیا فرض خطرات متناسب معتبر است؟ این فرض به این معنی است که نسبت خطرات برای هر دو فرد در جمعیت مورد مطالعه در طول زمان ثابت خواهد بود (جهت درک بهتر مفهوم خطرات Hazards این مقاله راهنما را ببینید). برای بررسی اعتبار این فرض، نرم‌افزار Prism دو نمودار ارایه می‌دهد. گراف باقیمانده‌های Schoenfeld مقیاس شده در مقابل زمان یا ترتیب ردیف، و همچنین نمودار بقای Log-minus-log.

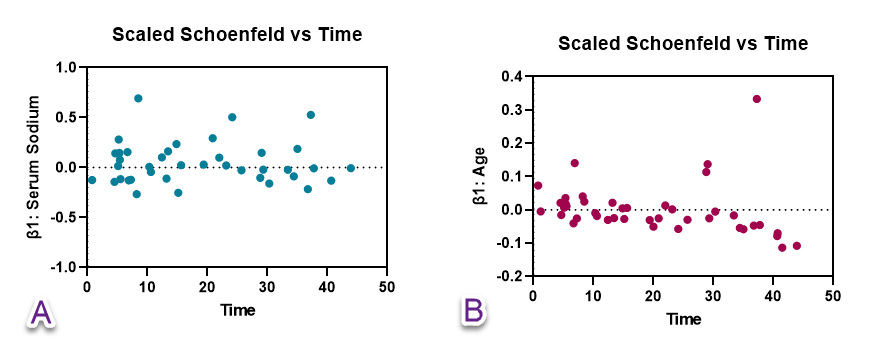
• Scaled Schoenfeld residuals vs. time/row order

اگر فرض خطرات متناسب معتبر باشد، باقیمانده‌های مدل رگرسیون کاکس باید به طور تصادفی در یک خط افقی اطراف صفر قرار گیرند. اگر روند قابل مشاهده‌ای در باقیمانده‌ها وجود داشته باشد، احتمالاً فرض خطرات متناسب نقض شده است.

به عنوان مثال گراف‌های زیر را نگاه کنید. در این گراف تصویر A بیانگر تایید شدن فرض خطرات متناسب و گراف B نشان‌دهنده رد شدن این فرضیه می‌باشد.

 

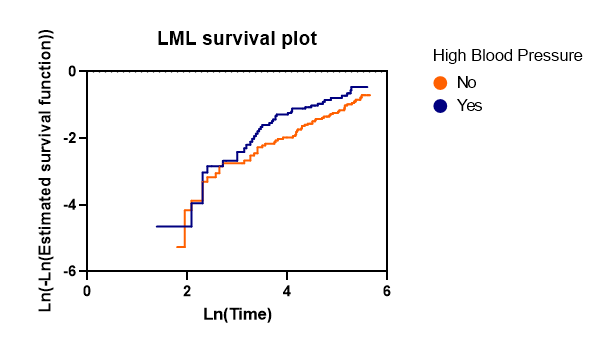
• Log-minus-log (LML) survival plot (Ln(-Ln(S(t))))

اگر مدل مشخص شده دارای کمیت‌های طبقه‌بندی باشد، این نمودار به شما امکان می‌دهد کمیت‌های طبقه‌بندی را برای ساختن نمودارهای LML انتخاب کنید. نمودار شامل یک منحنی برای هر گروه (سطح) در کمیت(های) طبقه‌بندی انتخاب شده است.

برای ایجاد این منحنی‌ها، از براورد خطر نلسون – آلن Nelson-Aalen hazard estimate جهت محاسبه خطر تجمعی هر گروه استفاده می‌شود. به یاد بیاورید که خطر تجمعی به صورت H(t) = -Ln(h(t)) تعریف می‌شود. با گرفتن Ln از براورد خطر تجمعی نلسون – آلن برای هر گروه، عبارت Ln(H(t)) یا Ln(-Ln(h(t))) را بدست می آوریم. این مقدار همان “log-minus-log” است که نام گراف به آن اشاره دارد و در محور Y قرار می‌گیرد. همچنین Ln(time) در محور X رسم می‌شود.

اگر فرض خطرات متناسب معتبر باشد، منحنی‌های هر گروه (سطح) کمیت پیش‌بینی‌کننده طبقه‌ای، تقریباً موازی خواهند بود. گراف زیر یک نمودار LML را نشان می‌دهد که منحنی‌های فشار خون بالا “دارد” و “ندارد” را با هم مقایسه می‌کنند. در حالی که خطوط در این نمودار کاملاً موازی نیستند، آنها نشان می‌دهند که فرض خطرات متناسب برای این مثال به شدت نقض نشده است. اگر منحنی‌های گروه‌ها (سطوح) در یک کمیت پیش‌بینی‌کننده طبقه‌بندی، با یکدیگر برخورد کنند، احتمالاً فرض خطرات متناسب نقض شده است و برقرار نیست.

 

برخی از نمودارهای باقیمانده در مدل خطرات متناسب Cox به منظور تشخیص نقاط پرت Outliers پیشنهاد شده است. نرم‌افزار Prism سه نمونه از این گراف‌ها را برای ما رسم می‌کند. در ادامه درباره‌ی آن‌ها توضیح می‌دهیم.

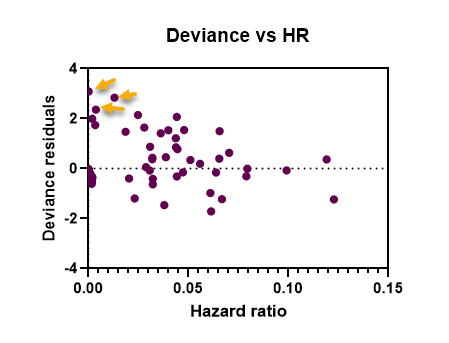
• Deviance residuals vs linear predictor/HR

در این گراف انحراف باقیمانده‌ها در برابر پیش‌بینی خطی از نسبت خطر (HR) رسم می‌شوند. نقاط این نمودار باید اطراف خط صفر قرار گیرند. در حالی که نقاط با باقیمانده قدرمطلق بزرگ ممکن است نقاط پرت را نشان دهند. توجه داشته باشید که روند مشاهده شده در این نمودارها ممکن است به دلیل حجم نمونه یا الگوهای ناکافی در نحوه سانسور مشاهدات باشد.

در گراف زیر یک نمونه نمودار Deviance residuals vs linear predictor/HR رسم شده است. مواردی که با فلش مشخص شده دارای باقیمانده‌های بزرگ هستند و می‌توانند به عنوان داده پرت شناخته شوند.

 

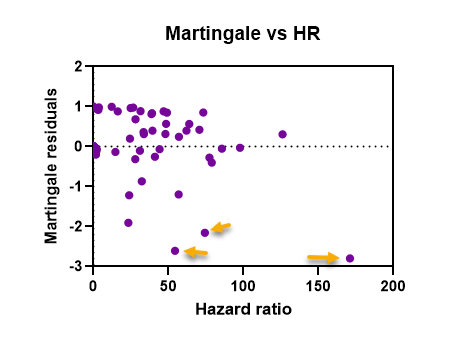
• Martingale residuals vs linear predictor/HR

در این گراف باقیمانده‌های مارتینگل در برابر پیش‌بینی خطی از نسبت خطر (HR) رسم می‌شوند. مانند گراف بالا، می‌توان از آن‌ها برای یافتن نقاط پرت در داده‌ها استفاده کرد. با این حال، این باقیمانده‌ها دارای انحراف هستند (نه در مرکز صفر). بلکه باقی‌مانده‌ها برای مشاهدات رویداد در محدوده [inf, 1-) و مشاهدات سانسور شده در محدوده [inf, 0). فهم این باقیمانده‌ها معمولاً سخت‌تر از گراف انحراف باقیمانده‌ها است.

در گراف زیر یک نمونه نمودار Martingale residuals vs linear predictor/HR رسم شده است. مواردی که با فلش مشخص شده دارای باقیمانده‌های بزرگ هستند و می‌توانند به عنوان داده پرت شناخته شوند.

 

• Schoenfeld residuals vs time or row order

از این گراف با نام باقیمانده‌های شوئنفلد در مقابل زمان یا ترتیب ردیف، یاد می‌شود. برخلاف باقیمانده‌های انحراف و مارتینگل، این باقیمانده‌ها به منظور بررسی تاثیر یک مشاهده بر هر یک از ضرایب رگرسیونی استفاده می‌شوند. هنگام انتخاب این گزینه، نموداری ایجاد می‌شود که به شما امکان می‌دهد باقیمانده‌های شوئنفلد را برای هر ضریب کمیت موجود در مدل کاکس بررسی کنید.

این نمودار همچنین ممکن است برای آزمایش فرض خطرات متناسب مورد استفاده قرار گیرد (اگر این نمودارها شیب غیر صفر داشته باشند، ممکن است فرض خطرات متناسب نقض شده باشد). در تصویر زیر می‌توانید یک نمونه از این گراف را مشاهده کنید.

 

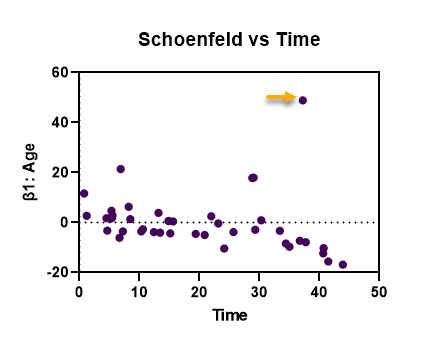
به عنوان مثال گراف بالا نشان می‌دهد، مشاهده‌ای که با فلش مشخص شده است دارای بیشترین تاثیر (مثبت) بر ضریب رگرسیونی Age در این مطالعه است.

نرم‌افزار Prism دو نمودار ارایه می‌دهد که می‌تواند جهت ارزیابی خطی بودن تاثیر کمیت‌های پیش‌بینی کننده بر مدل رگرسیون کاکس استفاده شود. همانند نمودارهایی که وجود نقاط پرت را بررسی می‌کنند، می‌توان از باقیمانده‌های انحراف یا مارتینگل استفاده کرد.

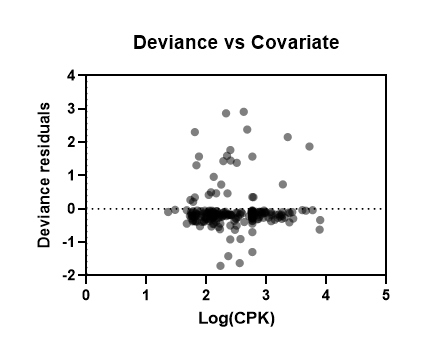
• Deviance residuals vs covariate

این گزینه یک نمودار ایجاد می‌کند که انحراف باقیمانده‌ها را در برابر هر یک از کمیت‌های پیش‌بینی (البته از نوع پیوسته) در مدل رسم می‌کند. انتظار می‌رود که انحراف باقیمانده‌ها به طور تصادفی حول محور صفر متمرکز شوند. مشاهده روند در این گراف ممکن است نشان دهنده انحراف از خطی بودن برای کمیت پیش‌بینی انتخاب شده باشد.

در تصویر زیر یک نمونه از این گراف‌ها را می‌توانید مشاهده کنید.

 

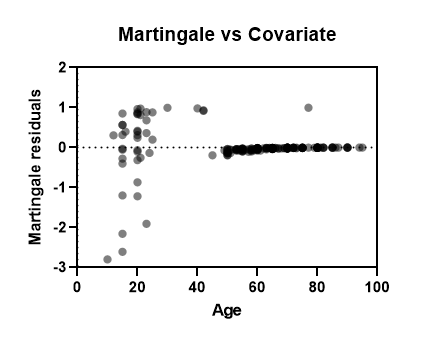
• Martingale residuals vs covariate

این گزینه گرافی از باقیمانده‌های مارتینگل در برابر کمیت‌های پیوسته موجود در مدل رسم می‌کند. این باقیمانده‌ها چوله هستند، در محدوده [inf, 1-) قرار می‌گیرند، با این حال همچنان باید میانگین صفر داشته باشند. روندهای قابل مشاهده در این گراف از باقیمانده‌های مارتینگل ممکن است نشان‌دهنده انحراف از خطی بودن برای کمیت پیش‌بینی کننده انتخابی باشد. به این نکته توجه کنید که تفسیر باقیمانده‌های مارتینگل سخت‌تر از گراف انحراف باقیمانده‌ها است. در تصویر زیر یک نمونه از این گراف را مشاهده کنید.

 

در این بخش به این سوال پاسخ می‌دهیم که مدل به دست آمده چقدر خوب است؟
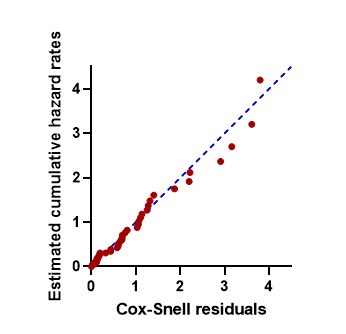
از این گراف با نام کاکس- اسنل در برابر نلسون-آلن از نرخ خطر تجمعی Cox-Snell vs Nelson-Aalen estimate of the cumulative hazard rate، یاد می‌شود. این نمودار در ابتدا برای استفاده در ارزیابی تناسب کلی یک مدل پیشنهاد شد. به این ترتیب که مدل رگرسیون مناسب یک خط تقریباً مستقیم از نقاط این نمودار ایجاد می‌کند که از مبدا می‌گذرد و دارای شیب یک است. با این حال، مشکل این نمودار این است که هیچ درکی در مورد اینکه چرا تناسب ضعیف بود (نقض فرض خطرات متناسب، موارد پرت، کمیت‌های وابسته به زمان) در اختیار ما قرار نمی‌دهد. در تصویر زیر یک نمونه از این گراف را مشاهده کنید.

 

 

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2023). Residuals in Cox proportional hazards regression. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/Cox-proportional-hazards-regression-residuals/.php

For example, if you viewed this guide on 12^th January 2023, you would use the following reference

GraphPad Statistics (2023). Residuals in Cox proportional hazards regression. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/Cox-proportional-hazards-regression-residuals/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.