رگرسیون لجستیک ترتیبی Ordinal Logistic Regression در نرم‌افزار SPSS

 Ordinal Logistic Regression 

دریافت مجموعه آموزش انواع مدل‌های رگرسیون لجستیک

شامل 130 دقیقه ویدئو، فایل‌های مثال، دیتا و نتایج SPSS

 

رگرسیون ترتیبی که نام کامل‌تر آن رگرسیون لجستیک ترتیبی است، هنگامی به کار می‌رود که کمیت پاسخ یا همان Y دارای اندازه‌های عددی ترتیبی Ordinal مانند کم، متوسط، زیاد، باشد.

به عنوان مثال در نظر بگیرید یک زیست‌شناس، مدت زمان زنده ماندن حیوانی را مطالعه می‌کند. او می‌خواهد تعیین کند آیا بقا به نوع منطقه و میزان سمیت آب مربوط است یا خیر. این زیست‌شناس زمان بقا را به سه دسته تقسیم می‌کند. کمتر از 10 روز، 11 تا 30 روز و بیش از 30 روز.

در این مطالعه، بقا به عنوان کمیت پاسخ یا همان Y مطرح است. نوع منطقه و سمیت آب نیز به صورت کمیت‌های مستقل یا همان Xها وارد مطالعه می‌شوند. از آنجا که پاسخ (بقا) یک کمیت ترتیبی است، زیست‌شناس از رگرسیون لجستیک ترتیبی در این مطالعه استفاده می‌کند.

تحلیل‌های جایگزین

Binary Logistic Regression

اگر کمیت پاسخ تنها دارای دو گروه باشد، مثلا شکست یا پیروزی، سالم یا بیمار. در این صورت مدل رگرسیونی ما لجستیک باینری Binary Logistic Regression خواهد بود. در این زمینه علاقمند بودید می‌توانید لینک (رگرسیون لجستیک باینری Binary Logistic Regression در نرم‌افزار SPSS) را ببینید.

Ordinal Logistic Regression

اگر کمیت پاسخ تنها دارای بیشتر از دو گروه رتبه‌ای Ordinal باشد، به عنوان مثال رده‌های کم، متوسط، زیاد. در این صورت مدل رگرسیونی ما لجستیک ترتیبی Ordinal Logistic Regression خواهد بود. در این زمینه می‌توانید لینک (رگرسیون لجستیک ترتیبی Ordinal Logistic Regression در نرم‌افزار Minitab) را مشاهده کنید.

Poisson Regression

اگر کمیت پاسخ قابل شمارش و تعداد رخداد یک پیشامد باشد، به عنوان مثال تعداد نقص‌ها در یک سیستم یا تعداد تصادفات. در این صورت مدل رگرسیونی ما پواسن Poisson Regression خواهد بود. علاقمند بودید لینک (تحلیل مدل رگرسیون پواسن Poisson Regression با نرم‌افزار گراف پد) را ببینید.

اگر کمیت پاسخ قابل شمارش و تعداد رخداد یک پیشامد باشد، به عنوان مثال تعداد نقص‌ها در یک سیستم یا تعداد تصادفات. در این صورت مدل رگرسیونی ما پواسن Poisson Regression خواهد بود.

مسیر انجام تحلیل رگرسیون ترتیبی

 SPSS 

مسیر انجام آنالیز رگرسیون لجستیک رتبه ای در نرم‌افزار SPSS به صورت زیر است.

Analyze→ Regression → Ordinal

مثال رگرسیون لجستیک ترتیبی

 Example 

فرض کنید مدیر یک بیمارستان می‌خواهد بداند چه عواملی بر رضایت بیماران اثرگزار است. او از بیماران سوال می پرسد که آن‌ها چه اندازه علاقمند هستند جهت ادامه درمان به این بیمارستان مراجعه کنند. پاسخ‌ها به صورت طیفی از بعید است، تاحدی محتمل است و بسیار احتمال دارد، قرار دارند. پیش‌بینیی کننده‌هایی مانند سن، وضعیت اشتغال و نزدیکی به بیمارستان نیز از بیماران پرسیده شده است.

مدیر بیمارستان از احتمال بازگشت بیمار به عنوان کمیت پاسخ (Y) استفاده می‌کند. دسته‌بندی‌های کمیت پاسخ دارای ترتیبی از بعید به احتمال زیاد هستند، بنابراین کمیت پاسخ رتبه‌ای یا همان Ordinal است و برای مدل‌سازی رابطه بین پیش‌بینی کننده‌ها (Xها) و پاسخ (Y) از رگرسیون لجستیک ترتیبی استفاده می‌شود.

فایل دیتای این مثال و نتایج به دست آمده با استفاده از نرم‌افزار SPSS را می‌توانید از اینجا دریافت کنید. در تصویر زیر می‌توانید بخشی از داده‌ها را مشاهده کنید.

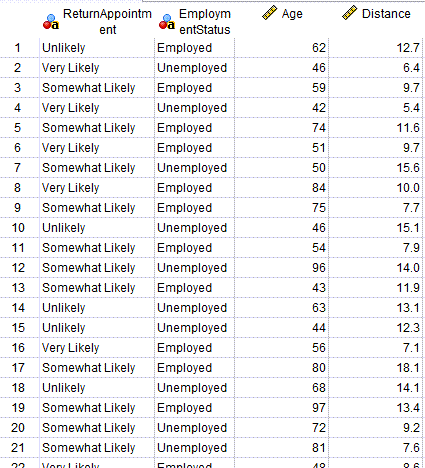
حال در ادامه با استفاده از مسیر زیر، به انجام آنالیز Ordinal Logistic Regression در نرم‌افزار SPSS می‌پردازیم.

Analyze→ Regression → Ordinal

پس از رفتن به این مسیر، پنجره Ordinal Regression برای ما باز می‌شود.

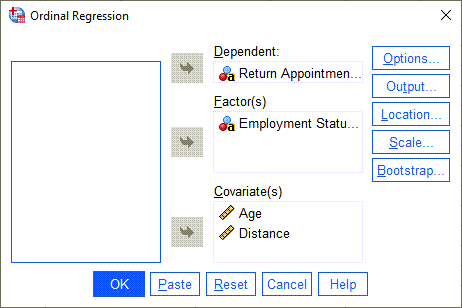
در این پنجره، ستون Return Appointment را به عنوان Dependent و ستون‌های Age و Distance را در کادر Covariate قرار می‌دهیم. همچنین وضعیت اشتغال نیز از آنجا که یک کمیت اسمی تعریف شده است در کادر Factor قرار می‌گیرد.

پنجره Ordinal Regression، تب‌های مختلفی دارد که ما معمولاً همان تنظیمات پیش‌فرض آن‌ها را می‌پذیریم و به آن‌ها در این مقاله کاری نداریم.

با این حال بر روی تب  بزنید تا وارد پنجره زیر شوید.

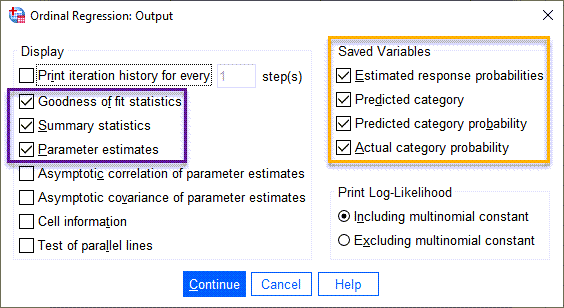
در این پنجره، علاوه بر گزینه‌های انتخاب پیش‌فرض SPSS، یعنی گزینه‌های Goodness of fit statistics و Summary statistics و Parameter estimates گزینه‌های کادر Save Variables را نیز انتخاب می‌کنیم.

در این بخش از نرم‌افزار می‌خواهیم، خروجی‌هایی مانند احتمال‌های پاسخ براورد شده، طبقه پیش بینی شده، احتمال طبقه پیش بینی شده و احتمال گروه واقعی را برای ما به دست بیاورد. این نتایج در همان فایل دیتا، قابل مشاهده خواهند بود. درباره نتایج آن‌ها بعداً و به هنگام به دست آمدن نتایج، بیشتر صحبت می‌کنیم.

در مرحله‌ی بعد Continue کرده و سپس OK می‌کنیم. با انجام این کار نتایج و خروجی‌های نرم‌افزار برای ما به دست می‌آید. در ادامه به بیان آن‌ها می‌پردازیم.

نتایج تحلیل رگرسیون ترتیبی

 Minitab Output 

در ابتدا جدول زیر با نام Case Processing Summary مشاهده می‌شود. در این جدول به ازای هر کدام از سطوح مختلف کمیت پاسخ یعنی Return Appointment فراوانی آن‌ها آمده است.

نتایج جدول بالا نشان می‌دهد 19 نفر بازگشت به بیمارستان برای ادامه فرایند درمان را با احتمال زباد، 43 نفر تاحدی محتمل و 11 نفر بعید دانسته‌اند. رویهم رفته 73 نفر نیز در این مطالعه مورد ارزیابی قرار گرفته‌اند.

جدول بعدی در نتایج نرم‌افزار با نام Model Fitting Information قرار دارد. آن را ببینید.

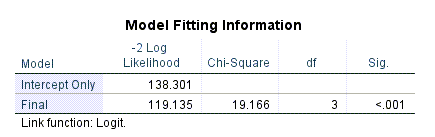
این نکته را می‌دانیم که هر کجا در نرم‌افزار ستونی با نام Sig می‌آید، فرضیه‌ای آزمون شده است. در اینجا فرضیه مورد آزمون که نتایج آن در سطر Final آمده است، صفر بودن همه ضرایب رگرسیونی است. به معنای اینکه هیچکدام از کمیت‌های مستقل (در این مثال وضعیت اشتغال، سن و فاصله تا محل سکونت) تاثیر معنادار بر احتمال بازگشت به بیمارستان را ندارند.

نتیجه به دست آمده P-value < 0.001 بیانگر رد این فرضیه و معنادار بودن حداقل یکی از کمیت‌های مستقل بر احتمال بازگشت است.

همانند تمام آزمون‌های نیکویی برازش Goodness of Fit فرض صفر، نیکو بودن برازش (مناسب بودن مدل) و فرض مقابل عدم نیکو بودن برازش ( مناسب نبودن مدل) است. بنابراین فرضیه‌ها به صورت زیر است.

در جدول زیر با نام Goodness-of-Fit نتیجه این فرضیه را ببینید.

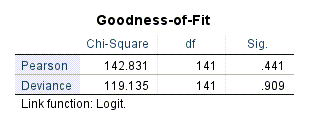
بر مبنای این جدول، روش‌ها و آزمون‌های نیکویی برازش Pearson و Deviance مورد بررسی قرار گرفته است. بیایید در ادامه به توضیح آن‌ها بپردازیم.

آزمون پیرسون و همچنین Deviance تناقض و تفاوت بین مدل فعلی برازش شده بر داده‌ها و مدل کامل را ارزیابی می‌کند. فرض صفر در این آزمون‌ها، نیکو بودن و مناسب بودن مدل برازش شده است. نتیجه به دست آمده بر مبنای آزمون نیکویی برازش پیرسن و مقدار احتمال به دست آمده، بیانگر تایید فرض صفر است و نشان می‌دهد، مدل به دست آمده مناسب است (P-Value = 0.441).

این نتیجه برای آزمون Deviance نیز برقرار است. بر مبنای مقدار احتمال به دست آمده نتیجه می‌گیریم مدل به دست آمده مناسب است (P-Value = 0.909).

در ادامه نتایج نرم‌افزار SPSS در تحلیل مدل رگرسیون چند جمله ای، جدول زیر با نام Pseudo R-Square را ببینید.

ما در هر مدل رگرسیونی عدد متناظر برای ضریب تعیین یا همان R Square را به دست می‌آوریم. بر مبنای این آماره می‌توانیم بگوییم که X ها تا چه اندازه‌ای از Y را می‌توانند بیان کرده و توضیح دهند.

در یک مدل رگرسیونی ترتیبی نیز با مفهومی به نام شبه ضریب تعیین که Pseudo R-Square نامیده می‌شود، روبه‌رو هستیم. در جدول بالا اعداد به دست آمده برای Pseudo R-Square بیان شده‌اند. این اعداد بیانگر مناسب بودت تقریبی مدل برازش شده هستند.

مهمترین جدول هر تحلیل رگرسیونی را می‌توان جدول پارامترها Parameter Estimates عنوان کرد. در تصویر زیر می‌توانید نتایج این جدول را مشاهده کنید.

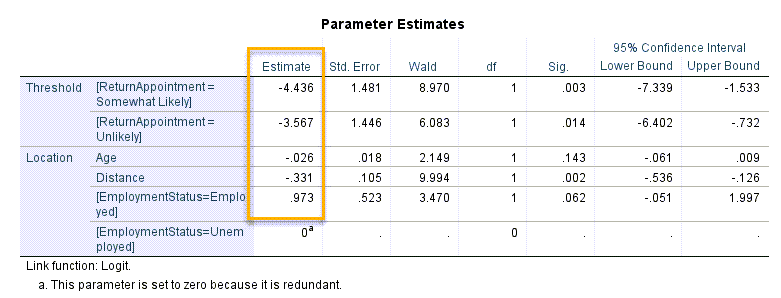
جدول بالا به دو بخش تقسیم می‌شود. یک بخش مربوط به آستانه (Threshold) که در نقاط برش Cut Points بررسی می‌شود و بخش دیگر با نام Location است که در آن براورد پارامترها به دست آمده است. در واقع ما همواره در حل هر مثال رگرسیون لجستیک ترتیبی، به تعداد یکی کمتر از تعداد گروه‌های تشکیل دهنده کمیت رتبه‌ای پاسخ، سطر در بخش Threshold خواهیم داشت. در این زمینه در ادامه بیشتر صحبت می‌کنیم.

اجازه دهید در ابتدا به بیان بخش Location در جدول بالا بپردازیم. یادتان باشد ما در این مثال رگرسیون ترتیبی، از دو کمیت مستقل یعنی Distance و Age به همراه یک فاکتور یعنی وضعیت اشتغال، جهت براورد و مدل‌بندی کمیت رتبه‌ای یعنی احتمال بازگشت به بیمارستان (در سه رده بعید است، تاحدی محتمل است و بسیار احتمال دارد) استفاده کردیم.

 Distance 

نتایج جدول بالا در سطر Distance را نگاه کنید. عدد ضریب رگرسیونی یا همان Estimate برابر با 0.331- شده است. منفی بودن آن بیانگر ارتباط وارون بین فاصله از بیمارستان و احتمال بازگشت به مرکز درمانی است.

به عبارت ساده هر چقدر منزل و محل سکونت بیمار از بیمارستان دورتر باشد، احتمال بازگشت او به مرکز درمان نیز کمتر است و هر چقدر او به بیمارستان نزدیک‌تر باشد، احتمال بازگشت او نیز بیشتر است. طبیعی است که این مطلب یک نتیجه منطقی است.

عدد P value به دست آمده نیز به صورت 0.002 شده است. این عدد بیانگر تاثیر معنادار Distance بر روی کمیت پاسخ یعنی Return Appointment است.

 Age 

حال بیایید همه این نتایج را بار دیگر برای کمیت مستقل دیگر مطالعه یعنی Age بررسی کنیم. اندازه عددی ضریب رگرسیونی آن منفی و برابر با 0.026- شده است. این عدد هر چند تاثیر اندک Age بر Return Appointment را نشان می‌دهد اما به هر حال بیانگر رابطه وارون سن و احتمال بازگشت است.

به نظر می‌رسد افراد دارای سنین بالاتر تمایل کمتری برای بازگشت به بیمارستان جهت ادامه درمان را دارند. البته به این نکته مهم توجه کنید که این رابطه غیرمعنادار به دست آمده است (P value = 0.143).

 Employment Status 

در این بخش افراد شاغل در مقایسه با افراد بیکار بررسی شده‌اند. اندازه عددی ضریب رگرسیونی مثبت و برابر با 0.973 نشان می‌دهد، افراد شاغل تمایل بیشتری برای بازگشت به این بیمارستان را دارند. این رابطه در سطح آلفا پنج درصد، غیرمعنادار به دست آمده است (P value = 0.062).

 Threshold 

در جدول Parameter Estimates علاوه بر نتایج مربوط به کمیت‌های Distance و Age و وضعیت اشتغال، دو سطر دیگر نیز مشاهده می شود. نرم‌افزار SPSS نام آن‌ها را به صورت Threshold آورده است.

یک سوال. چرا ما در این مثال دو ضریب رگرسیونی با نام Threshold داریم؟ پاسخ ساده است. به دلیل اینکه سه رتبه برای کمیت پاسخ احتمال بازگشت تعریف شده است. در واقع در هر تحلیل رگرسیون ترتیبی با نرم‌افزار SPSS به تعداد یکی کمتر از رتبه‌های Response ضریب رگرسیونی با نام Threshold خواهیم داشت.

شاید سوال دیگر این باشد حالا چرا یکی کمتر؟ پاسخ این است که آن‌ها به فاصله و اختلاف بین هر دو رتبه در Response اشاره می کنند. یعنی Threshold(1) به فاصله بین احتمال تاحدی محتمل است و احتمال خیلی زیاد و Threshold(2) به احتمال خیلی بعید و تاحدی محتمل است، اشاره می‌کنند.

یک تعبیر جالب توجه این است که می‌توان Threshold ها را Cutoff یا نقطه برش دانست. بیایید Threshold(1) را توضیح دهیم. عدد آن برابر با 4.436- شده است. این عدد نشان می‌دهد که اگر برای یک فرد فرضی، اندازه عددی Response در مدل رگرسیونی کمتر از 4.436- شود، آن فرد در رده افراد با احتمال بازگشت خیلی زیاد، قرار می‌گیرد.

به همین ترتیب اگر عدد Response در مدل رگرسیونی بین اعداد Threshold(1) تا Threshold(2) یعنی 3.567- باشد، آن فرد در رتبه افراد تاحدی محتمل قرار می‌گیرد.

برای افراد دارای Response بزرگتر از 3.567- نیز آن فرد در رده افراد دارای احتمال خیلی بعید در بازگشت به بیمارستان قرار خواهد گرفت.

فایل داده‌ها پس از تحلیل

 Data File 

به خاطر داشته باشید در تب  از نرم‌افزار خواستیم، خروجی‌هایی مانند احتمال‌های پاسخ براورد شده، طبقه پیش بینی شده، احتمال طبقه پیش بینی شده و احتمال گروه واقعی را برای ما به دست بیاورد. این نتایج در فایل دیتا، قابل مشاهده هستند. در تصویر زیر بخشی از آن‌ها را ببینید.

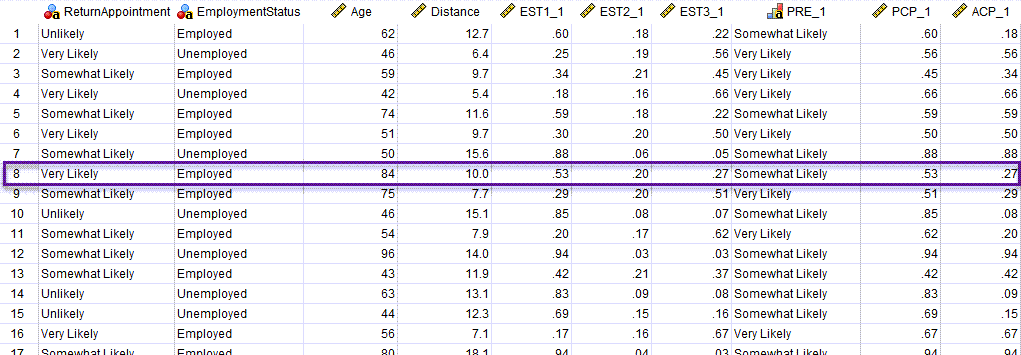
در این فایل ستون‌های با نام EST2 ،EST1 و EST3 متناظر با گزینه‌ی Estimated response probabilities در تب  به دست آمده‌اند. هر کدام از ستون‌های EST به احتمال تعلق فرد به یکی از گروه‌های به ترتیب Somewhat Likely و Unlikely و Very Likely (به ترتیب حروف الفبا) بیان می‌شوند.

به عنوان مثال برای فرد هشتم که خودش ابراز علاقه زیادی برای بازگشت کرده است، بر مبنای مدل رگرسیونی به دست آمده، تاحدی محتمل برابر با 53%، خیلی بعید 20% و احتمال بازگشت خیلی زیاد 27% به دست آمده است. این نتایج از همان ستون‌های EST2 ،EST1 و EST3 به دست می‌آید.

ستون دیگر با نام PRE در فایل دیتا وجود دارد. نتایج این ستون به دلیل انتخاب گزینه Predicted category در تب  به دست آمده است. بر مبنای این ستون، هر فرد به یک رده احتمال بازگشت، تعلق گرفته است. این تعلق بر مبنای بزرگترین احتمال در ستون‌های EST2 ،EST1 و EST3 است. به عنوان مثال برای همان فرد هشتم بیشترین احتمال عدد 53% مربوط به تاحدی محتمل بوده است. به همین دلیل این فرد بر مبنای مدل رگرسیون لجستیک ترتیبی در گروه احتمال بازگشت تا حدی مجتمل، قرار گرفته است.

PCP ستون دیگر در فایل دیتا است. نتایج این ستون نیز به دلیل انتخاب گزینه Predicted category probability به دست آمده‌اند. چنانچه دقت کنید داده‌های این ستون همان بزرگترین عدد در ستون‌های EST2 ،EST1 و EST3 است. به عبارت دیگر اعداد این ستون را می‌توان، احتمال قرار گرفتن هر فرد در ستون PRE دانست.

در نهایت در فایل دیتا ستون ACP قرار دارد. نتایج این ستون به دلیل انتخاب گزینه Actual category probability به دست آمده‌اند. فهم آن نیز بسیار ساده است. اعداد این ستون احتمال قرار گرفتن هر فرد در احتمال بازگشت واقعی و مشاهده شده یعنی همان رده‌ای که خود فرد بیان کرده است را نشان می‌دهد. به عنوان مثال فرد شماره هشت، گفته است که احتمال بازگشت او به این بیمارستان خیلی زیاد است. این مطلب از ستون Return Appointment مشخص می‌شود. حال بر مبنای مدل چند رگرسیون رتبه ای به دست می‌آید که احتمال اینکه این فرد به احتمال خیلی زیاد برگردد برابر با 27% است.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2021). Ordinal Logistic Regression in SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/ordinal-logistic-regression-spss/.php

For example, if you viewed this guide on 12^th January 2022, you would use the following reference

GraphPad Statistics (2021). Ordinal Logistic Regression in SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/ordinal-logistic-regression-spss/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.