ضریب همبستگی اسپیرمن Spearman Correlation Coefficient در نرم‌افزار SPSS

توضیحات برگرفته شده از کتاب روش های پیشرفته آماری و کاربردهای آن

دریافت ویدئو آموزش تحلیل‌های همبستگی با SPSS

شامل 100 دقیقه ویدئو، 34 اسلاید، فایل‌های دیتا و نتایج نرم‌افزار SPSS

 

هر چقدر قدر مطلق ضریب همبستگی به عدد یک نزدیک‌تر باشد (در جهت مثبت یا در جهت منفی) ارتباط بین کمیت‌ها بیشتر و کامل‌تر است. وقتی اندازه عددی ضریب همبستگی به مقادیر مثبت یک نزدیک است به معنای وجود ارتباط قوی و مستقیم است، به نحوی که افزایش یک کمیت افزایش کمیت دیگر را در پی دارد و یا کاهش آن سبب کاهش کمیت دیگر می‌شود.

به همین‌ترتیب اندازه عددی ضریب همبستگی نزدیک به مقادیر منفی یک به معنای وجود یک ارتباط قوی و وارون است که اندازه‌های عددی دو کمیت در جهت عکس یکدیگر رفتار می‌کنند. اندازه‌های عددی نزدیک به صفر نیز بدان معنا است که تغییرات یک کمیت، اطلاع کمی درباره تغییرات کمیت دیگر در اختیار ما قرار می‌دهد. نکته‌ای که باید در این میان به آن توجه کرد این است که ضریب همبستگی صفر و یا نزدیک صفر را نباید به مفهوم استقلال کمیت‌ها از یکدیگر دانست. هر چند که ضریب همبستگی دو کمیت مستقل از یکدیگر، همواره صفر است.

انواع ضرایب همبستگی

همان گونه که می‌دانیم مشاهدات در چهار دسته‌ی اسمی Nominal، رتبه‌ای Ordinal، فاصله‌ای Interval و نسبتی Ratio طبقه‌بندی می‌شوند. خوب است این نکته را بدانید که نرم‌افزار SPSS به داده‌های از نوع فاصله‌ای و نسبتی اصطلاحاً Scale می‌گوید. براساس این دسته‌بندی‌ها انواع مختلف همبستگی بین کمیت‌ها و داده‌ها معرفی می‌شوند. در واقع مبنای ایجاد و معرفی ضرایب همبستگی مختلف تا حد زیادی متأثر از ماهیت و مقیاس اندازه‌گیری میان کمیت‌ها است. من در این متن قصد دارم به یکی از مهم‌ترین  انواع ضرایب همبستگی یعنی پیرسن Pearson بپردازم.

ضریب همبستگی اسپیرمن

 Spearman Correlation Coefficient 

ضریب همبستگی پیرسن تنها وجود یا عدم وجود رابطه خطی بین کمیت‌ها را نشان می‌دهد، در صورتی‌که ضریب همبستگی اسپیرمن می‌تواند وجود هرگونه رابطه میان کمیت‌ها را نشان دهد. آزمون ضریب همبستگی اسپیرمن ناپارامتری است و معمولاً به منظور تعیین ارتباط بین داده‌های کمی و رتبه‌ای استفاده می‌شود. با توجه به اینکه آماره این ضریب همبستگی، ناپارامتری است، معمولاً می‌توان بدون توجه به نرمال بودن مشاهدات، از ضریب همبستگی اسپیرمن استفاده کرد. هرچند در آمار پیشرفته‌تر اثبات می‌شود توزیع مجانبی آماره ضریب همبستگی اسپیرمن دارای توزیع تقریبی نرمال است.

همان‌گونه که در بحث فرضیه‌های آماری بیان کردیم، فرض صفر تفکر و ایده اولیه محقق از پژوهش خود می‌باشد، این فرض در پی پذیرش وضع موجود بوده و عدم ارتباط میان کمیت‌ها را بیان می‌کند. فرضیه مربوط به ضرایب همبستگی به صورت زیر است.

$ \displaystyle {{H}_{0}}:\rho =0\begin{array}{*{20}{c}} {} & {vs} & {} \end{array}{{H}_{1}}:\rho \ne 0$

فرض صفر این آزمون عدم ارتباط میان کمیت‌ها و فرض مقابل وجود ارتباط و ایجاد ساختار جدید را نشان می‌دهد. فراموش نکنیم که این آزمون می‌تواند علاوه بر تعریف دو دامنه (به صورت زیر) به صورت آزمون فرضیه‌های یک‌طرفه نیز تعریف شود.

 بیایید این بحث را با استفاده از نرم‌افزار SPSS توضیح دهیم. فایل دیتای این مثال را می‌توانید از اینجا دریافت کنید. ما در این مثال در پی آن هستیم که ارتباط بین تعداد ساعات مطالعه قبل از یک آزمون و رتبه‌ نهایی داوطلبان در آزمون را بسنجیم، به این منظور مطالعه‌ای بر روی 35  نفر که در آزمون شرکت کرده‌اند، انجام شده است.

در تصویر زیر می‌توانید بخشی از داده‌ها را مشاهده کنید.

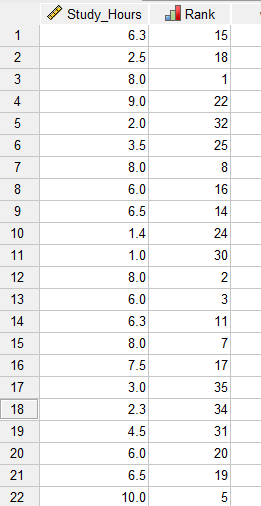
ستون با نام Rank رتبه فرد در آزمون است. از آن‌جا که این Variable یک کمیت رتبه‌ای و Ordinal است، بنابراین به سمت استفاده از آزمون همبستگی اسپیرمن می‌رویم. علاوه بر آن خوب است آزمون نرمال بودن داده‌های تعداد ساعات مطالعه نیز انجام شود.

جهت انجام آزمون نرمالیتی از مسیر زیر در نرم‌افزار SPSS استفاده می‌کنیم.

Analyze → Nonparametric Tests → Legacy Dialogs → 1-Sample K-S

با رفتن به این مسیر، پنجره زیر با نام One-Sample Kolmogorov-Smirnov Test برای ما باز می‌شود.

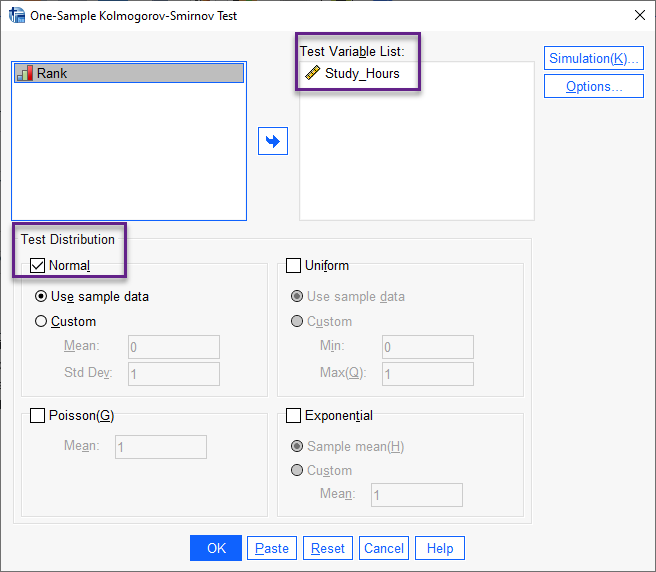
در کادر Test Variable List کمیت‌ تعداد ساعات مطالعه را که می‌خواهیم آزمون نرمالیتی بر روی آن انجام شود قرار می‌دهیم. همچنین در کادر Test Distribution گزینه Normal را انتخاب می‌کنیم. این کار سبب می‌شود، نرم‌افزار SPSS به انجام آزمون نرمالیتی بر روی ستون تعداد ساعات مطالعه بپردازد. OK کنید و نتایج را در پنجره Output نرم‌افزار ببینید.

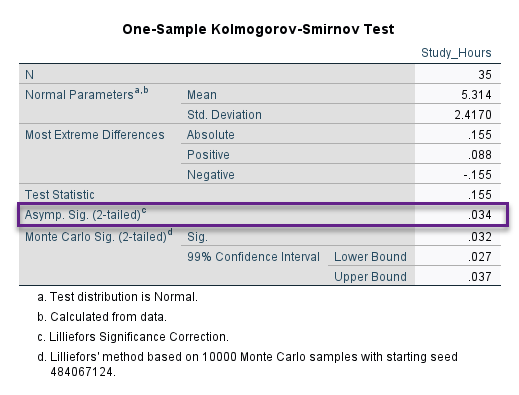
نتیجه به دست آمده در جدول بالا نشان می‌دهد تعداد ساعات مطالعه، فاقد توزیع نرمال در سطح معنی‌داری 0.05 درصد است (P-value = 0.034). به همین دلیل مناسب است جهت سنجش همبستگی بین رتبه فرد در آزمون و تعداد ساعت‌های مطالعه او از ضریب همبستگی اسپیرمن، استفاده می‌کنیم.

مسیر انجام تحلیل همبستگی در نرم‌افزار SPSS به صورت زیر است.

Analyze → Correlate → Bivariate 

پنجره زیر با نام Bivariate Correlation برای ما باز می‌شود.

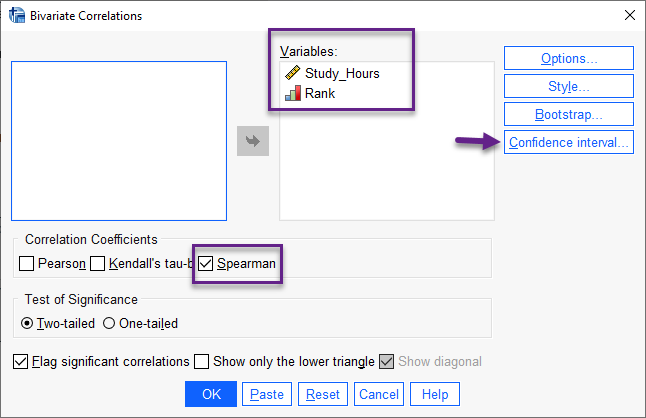
در کادر Variables همان کمیت‌هایی را که می‌خواهیم ضریب همبستگی بین آن‌ها به دست بیاید، قرار می‌دهیم. از آن‌جا که Rank یک Variable رتبه‌ای است و همچنین تعداد ساعات مطالعه نیز فاقد توزیع نرمال است، بنابراین در بخش Correlation Coefficients ضریب همبستگی اسپیرمن Spearman را انتخاب می‌کنیم.

چنانچه علاقمند باشیم، علاوه بر عدد ضریب همبستگی، فواصل اطمینان آن‌ها را نیز به دست بیاوریم، بر روی تب Confidence interval می‌زنیم. با این کار وارد پنجره زیر می‌شویم.

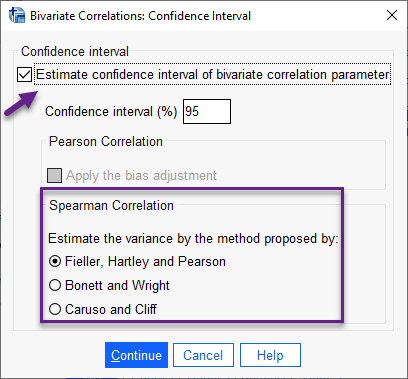
در این پنجره گزینه Estimate confidence interval of bivariate correlation parameter را انتخاب می‌کنیم. فاصله اطمینان را نیز می‌توانیم به دلخواه بر روی 95% قرار دهیم. در کادر Spearman Correlation می‌توانیم یکی از روش‌های براورد واریانس که در یافتن فاصله اطمینان به کار می‌رود را انتخاب کنیم. نرم‌افزار SPSS به صورت پیش‌فرض بر روی روش Fieller, Hartley and Pearson قرار دارد.

نتایج و خروجی‌های نرم‌افزار

 Output 

Continue کرده و سپس OK می‌کنیم. به این ترتیب نتایج و خروجی‌های زیر در Output نرم‌افزار SPSS به دست می‌آید.

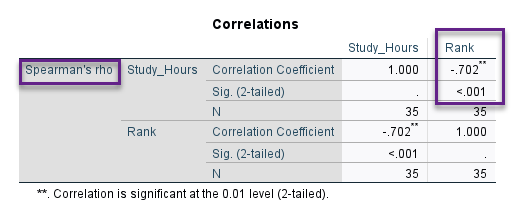
در جدول بالا می توانید عدد ضریب همبستگی اسپیرمن به همراه مقدار احتمال معناداری Sig را مشاهده کنید. نتایج این جدول نشان می‌دهد

$ \displaystyle {{r}_{{\left( {Spearman} \right)}}}=-0.702,\begin{array}{*{20}{c}} {} \end{array}P-value<0.001$

همچنین فواصل اطمینان ضرایب همبستگی اسپیرمن نیز در جدول زیر به دست آمده است.

به عنوان مثال فاصله اطمینان 95% برای ضریب همبستگی اسپیرمن بین Rank و Study_Hours برابر با (0.472- ,0.842-) به دست آمده است. نکته مهمی که در مبحث فواصل اطمینان ضرایب همبستگی مطرح است، این است که اگر این فاصله عدد صفر را در بر داشته باشد به معنای این است که رابطه همبستگی بین دو کمیت مورد بررسی، معنادار نیست. اما اگر فاصله اطمینان عدد صفر را در بر نداشته باشد به معنای وجود رابطه معنادار همبستگی بین آن‌ها می‌باشد.

در این مثال هم کران پایین و هم کران بالا، کمتر از صفر هستند. بنابراین نتیجه می‌گیریم (بدون مشاهده عدد ضریب همبستگی اسپیرمن و مقدار احتمال آن) رابطه بین رتبه فرد و ساعت‌های مطالعه، معنادار و منفی است.

نمودارهای پراکنش

 Scatter Plots 

در مطالعات و موضوعات مرتبط با ضرایب همبستگی، رسم نمودارهای پراکنش و یا همان Scatter Plot خود را نشان می‌دهد. نمودارهای پراکنش می‌توانند به ما فهم بهتر و دقیق‌تری از نحوه ارتباط بین Variableها ارایه کنند. آن‌ها را می‌توانیم با استفاده از مسیر زیر در نرم افزار SPSS رسم کنیم.

Graphs → Chart Builder 

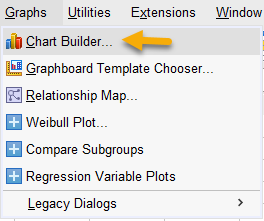
با رفتن به این مسیر، پنجره زیر با نام Chart Builder که جهت رسم و طراحی انواع گراف‌هایی آماری از آن استفاده می‌شود، برای ما باز می‌شود. در این پنجره و محیط نرم افزار SPSS قابلیت و امکنات فراوانی جهت ترسیم انواع نمودارهای آماری قرار داده شده است. نمودار پراکنش در تصویر زیر مشخص شده است.

به عنوان مثال من می‌خواهیم نمودار پراکنش بین Rank و Study_Hours را به دست بیاورم. مطابق تصویر بالا آن‌ها را قرار می‌دهم. من در این نمودار Rank را در محور x، و Study_Hours را در محور y، قرار داده‌ام. گراف به دست آمده را می‌توانید در شکل زیر ببینید.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2022). Spearman Correlation Coefficient in SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/spearman-correlation-coefficient-spss/.php

For example, if you viewed this guide on 12^th January 2022, you would use the following reference

GraphPad Statistics (2022). Spearman Correlation Coefficient in SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/spearman-correlation-coefficient-spss/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.