تحلیل مولفه‌های اصلی Principal Component Analysis (PCA) در نرم‌افزار Prism

در تحلیل آماری استنباطی مفهومی به نام تحلیل مولفه اصلی یا تحلیل عاملی (PCA) Principal Component Analysis وجود دارد. این آنالیز یک تکنیک چندگانه Multivariate است که به منظور کاهش ابعاد یک مجموعه داده و در عین حال حفظ تا حد امکان اطلاعات از داده‌ها استفاده می‌شود.

به عبارت ساده‌تر ما از روش تحلیلی PCA استفاده می‌کنیم تا بتوانیم تعداد Variableهای خود را تا حد امکان کاهش دهیم و آن‌ها را در چند مولفه Component اصلی و اثرگزار خلاصه نماییم.

معمولاً PCA با نرم‌افزاری مانند SPSS انجام می‌شود. از لینک (تحلیل عاملی با نرم‌افزار SPSS) می‌توانید آموزش کار با این نرم‌افزار را مشاهده و دریافت کنید.

با این حال من در این مقاله به دنبال آن هستم که به آموزش تحلیل مولفه اصلی با استفاده از نرم‌افزار GraphPad Prism بپردازم. این امکانی است که گراف پد در ورژن‌های جدید 9 به بعد خود، آن را اضافه کرده است.

اگرچه Prism تمام کارهای تحلیلی را از نظر پردازش و محاسبات انجام می‌دهد، با این حال درک اصول اولیه مفاهیم می‌تواند هنگام بیان نتایج PCA مفید باشد. اگر می‌خواهید از تئوری‌ها صرف‌نظر کنید و مستقیماً به تحلیل داده‌ها بپردازید، این مقاله راهنمای خوبی برای شما خواهد بود و به شما کمک می‌کند تا نتایجی را که PCA ایجاد می‌کند درک کنید.

برای شروع کار با مثال نرم‌افزار Prism آغاز می‌کنیم. این مثال را می‌توانید در تحلیل‌های Multiple variables نرم‌افزار ببینید. فایل دیتا همراه با تحلیل‌های انجام شده را می‌توانید از اینجا با نام Principal Component Analysis دریافت کنید.

مثال Principal Component Analysis (PCA) در گراف پد

من در تصویر زیر بخشی از فایل دیتا را آورده‌ام.

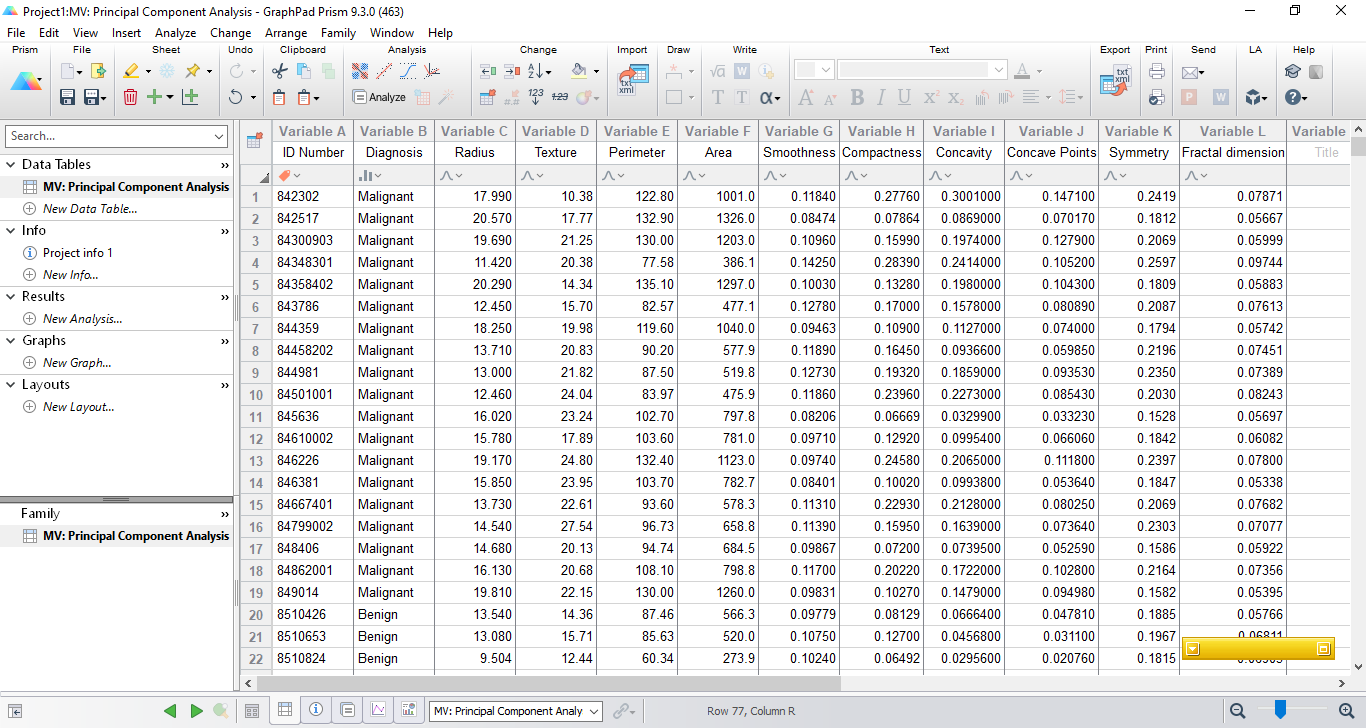
فایل دیتا مثال Principal Component Analysis (PCA)

این داده‌ها با مطالعه تصاویر سلول‌های بیوپسی بافت سرطان سینه جمع‌آوری شده است. تعداد 12 کمیت Variable برای هر تصویر نمونه ثبت شد که شامل: 1) شماره شناسه بیمار، 2) تشخیص (بدخیم یا خوش خیم)، 3) شعاع سلول، 4) بافت سلول، 5) محیط سلول، 6) ناحیه سلول، 7) سلول صافی، 8) فشردگی سلول، 9) تقعر سلول، 10) نقاط مقعر، 11) تقارن سلول، و 12) بعد فراکتال سلول، می‌باشد.

هدف از این مطالعه این است که بتوانیم با استفاده از تحلیل (PCA) تعداد Variableها مورد نیاز برای توصیف مناسب داده‌ها، کاهش دهیم و بر مبنای مجموعه کوچکی از اجزای اصلی ایجاد شده (3-2 مولفه)، به پیش‌بینی بدخیم یا خوش‌خیم بافت سرطانی، بپردازیم.

مراحل انجام تحلیل مولفه‌های اصلی در Prism

To run principal component analysis (PCA)

در ادامه مراحل انجام PCA در نرم‌افزار گراف پد را آورده‌ام. سعی می‌کنم هر یک را با جزئیات بیان کنم.

1 در شیت دیتا و در منوی Analysis بر روی گزینه Analyze می‌زنیم. البته می‌توانیم به صورت مستقیم نیز ابزارک Principal Component Analysis انتخاب کنیم.

در این صورت وارد پنجره زیر با نام Analyze Data می‌شویم.

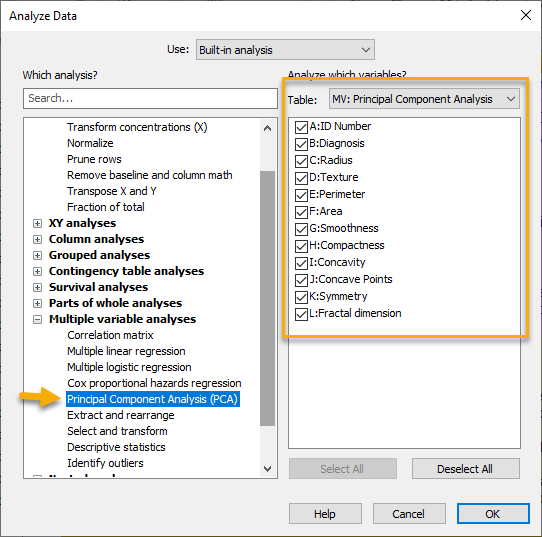
پنجره Analyze Data و انتخاب گزینه تحلیل عاملی

از آن‌جا که PCA یک تحلیل از نوع Multiple است، بنابراین در گزینه‌های Multiple variable analyses قرار دارد. آن را انتخاب می‌کنیم. در سمت راست پنجره بالا نیز اسامی Variable های موجود در مطالعه آمده است. چنانچه احیاناً خواستیم یک یا چند کمیت در مطالعه قرار نگیرد، تیک آن‌ها را بر می‌داریم. با OK کردن وارد پنجره زیر می‌شویم.

2 در پنجره Parameters Principal Component Analysis (PCA) به انتخاب تنظیمات نرم‌افزار جهت تحلیل مولفه‌های اصلی، می‌پردازیم.

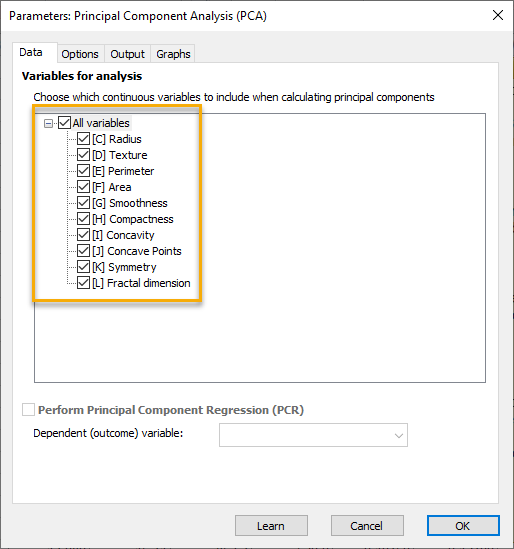
Data

در ابتدا تب Data مشاهده می‌شود. در این تب Variableهایی که در تحلیل قرار می‌گیرند، آمده است. این کمیت‌ها اندازه‌های عددی پیوسته هستند. همان‌گونه که مشاهده می‌کنید ستون‌های Patient ID Number که بیانگر کد شناسایی هم بیمار و Diagnosis که کمیت وابسته مطالعه است، در این تب قرار ندارند. در واقع تحلیل عاملی صرفاً بر روی کمیت‌های مستقل Independent Variable انجام می‌شود.

Options

در تب Options، شما باید دو تصمیم اصلی بگیرید که می‌تواند بر نتایج و نتیجه‌گیری های PCA تأثیر بگذارد. توصیه می‌کنیم PCA را روی داده‌های استاندارد شده Standardized Data انجام دهید و از تحلیل موازی Parallel Analysis برای انتخاب تعداد مولفه‌ها استفاده کنید.

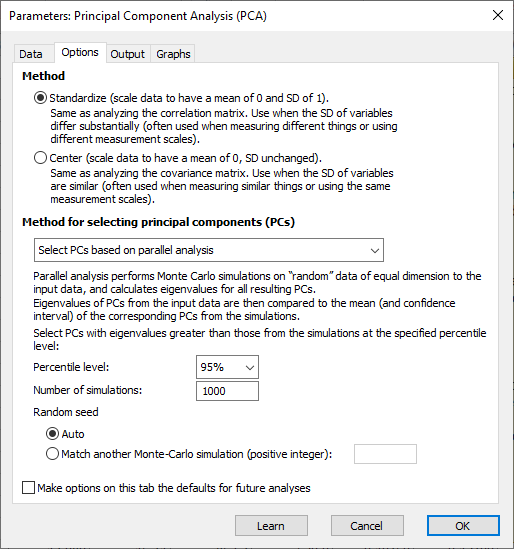
مهمترین تصمیم این است که آیا PCA روی داده های استاندارد شده یا متمرکز Centered Data انجام شود. من هر یک را در ادامه توضیح می‌دهم.

PCA on Standardized Data

همان‌گونه که بالاتر گفتم، این یک کار توصیه شده است. اگر Variableها با استفاده از واحدهای مختلف اندازه‌گیری شوند، تقریباً همیشه این رویکرد را انتخاب می‌کنیم. از دیدگاه ریاضی، استاندارد کردن داده‌ها بسیار ساده است. هر مشاهده منهای میانگین ستون خودش می‌شود و سپس بر انحراف معیار تقسیم می‌شود.

$X_{Standardized} = \left ( X_{raw} - \overline{X}\right )/S_{X}$

این کار سبب می‌شود داده‌ها هم‌وزن و هم واحد شده و میانگین و انحراف معیار آن‌ها به ترتیب برابر با صفر و یک شود.

PCA on Centered Data

چنانچه همه کمیت‌ها Variableها، هم واحد باشند، ممکن است بخواهید از این روش استفاده کنید. البته این اتفاق نادر است. از دیدگاه ریاضی متمرکز کردن داده‌ها به صورت زیر انجام می‌شود.

$X_{Centered} = \left ( X_{raw} - \overline{X}\right )$

این کار باعث می‌شود میانگین داده‌های جدید صفر و انحراف معیار آن‌ها مانند قبل بماند. با این حال از آنجایی که Variableها مقیاس‌بندی نشده‌اند، کمیت‌هایی با انحرافات استاندارد بزرگ‌تر نسبت به بقیه، بر روی تحلیل مولفه‌های اصلی اثرگزار هستند.

انتخاب مؤلفه‌های اصلی فرآیندی است که تعیین می‌کند مجموعه داده کاهش‌یافته بعد از PCA چند «بعد» خواهد داشت. Prism چهار روش را برای انتخاب تعداد اجزای اصلی ارائه می‌دهد. در تصویر زیر آن‌ها را می‌بینید.

روش‌های نرم‌افزار جهت انتخاب مولفه های اصلی

Paralell analysis (recommended)

در ابتدا متد آنالیز موازی یا همان Parallel analysis دیده می‌شود. این روش بر مبنای یک فرایند شبیه‌سازی شده، تعداد مولفه‌های اصلی Principal Component (PC) را تعیین می‌کند. به صورت خلاصه نحوه شبیه‌سازی آنالیز موازی را بیان کرده‌ام.

1. نرم‌افزار Prism تعداد زیادی مجموعه داده Dataset را شبیه‌سازی می‌کند (عدد 1000 پیش‌فرض است، اما می‌توان تعداد متفاوتی را مشخص کرد). هر مجموعه داده شبیه‌سازی شده، شامل همان تعداد Variable (ستون) و مشاهدات (ردیف) داده‌های اصلی است. به عنوان مثال در این مطالعه، هر Dataset شبیه‌سازی شده شامل 10 کمیت و 569 مشاهده است.

الف. برای هر Variable شبیه‌سازی شده، داده‌ها با نمونه‌گیری از یک توزیع نرمال چند بعدی Multidimensional Normal با میانگین = 0 تولید می‌شوند.

ب- انحراف استاندارد برای هر Variable شبیه‌سازی شده برابر با انحراف معیار کمیت مربوطه در داده‌های اصلی است.

2. PCA برای هر مجموعه داده شبیه‌سازی شده انجام می‌شود.

3. برای هر مولفه اصلی PC، میانگین مقدار ویژه Eigenvalue در تمام مجموعه داده‌های شبیه‌سازی شده محاسبه می‌شود. فهم این بخش ساده است. زیرا ما 1000 شبیه‌سازی انجام دادیم، بر روی هر کدام PCA گرفتیم و بنابراین برای هر PC، اکنون 1000 مقدار ویژه داریم، پس می‌توانیم به سادگی از آن‌ها میانگین بگیریم.

توضیح اینکه مقدار ویژه اندازه واریانس و پراکندگی است که هر مولفه از داده‌ها بیان می‌کند. بنابراین هر چقدر این عدد بزرگتر باشد به معنای این است که آن مولفه اندازه و حجم بیشتری از داده‌ها را در اختیار خود خواهد داشت.

4. برای هر PC، صدک بالا (صدک 95 به طور پیش فرض) مقادیر ویژه از همه مجموعه داده‌های شبیه‌سازی شده محاسبه می‌شود. از آن‌جا که ما 1000 مقدار ویژه داریم، بنابراین به دست آوردن صدک 95 نیز ساده است.

5. برای هر PC نرم‌افزار Prism، مقدار ویژه به دست آمده از داده‌های اصلی را با صدک 95 محاسبه شده از مجموعه داده‌های شبیه‌سازی شده مقایسه می‌کند.

6. برای هر PC اگر مقدار ویژه داده‌های اصلی بزرگتر از صدک 95 داده‌های شبیه‌سازی شده باشد، آن PC انتخاب می‌شود، در غیر این صورت PC انتخاب نمی‌شود.

توجه داشته باشید که اگر تحلیل موازی را برای تعیین تعداد PCها انتخاب کنید، نمودار Scree مقادیر ویژه شبیه‌سازی شده را به همراه مقادیر ویژه داده‌های شما نمایش می‌دهد. در تصویر زیر می‌توانید، تنظیمات Parallel analysis را که با استفاده از آن‌ها می‌توانیم تعداد شبیه‌سازی‌ها و سطح صدک را قرار دهیم، مشاهده کنیم.

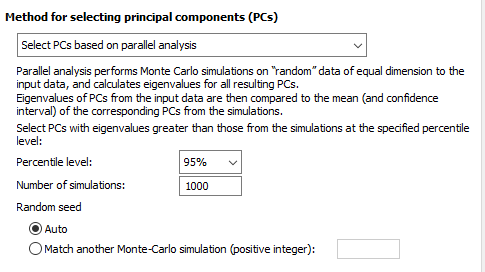
Select PCs based on eigenvalues

به طور کلاسیک، PCها بر مبنای مقادیر ویژه بیشتر از 1 انتخاب می‌شوند. به این قانون قیصر Kaiser rule می‌گویند. عمده نرم‌افزارهای آماری مانند SPSS از همین روش استفاده می‌کنند. انگیزه استفاده از «1» به عنوان نقطه برش این است که با داده‌های استاندارد شده، انحراف (و واریانس) استاندارد هر Variable برابر با 1 است. مقادیر ویژه برای PCها، واریانسی را که هر مولفه از داده‌های اصلی نشان می‌دهد، بیان می‌کنند. بنابراین، اگر مقدار ویژه یک مولفه کمتر از 1 باشد، پس پراکندگی کمتری را نسبت به یک Variable توضیح می‌دهد. در نتیجه نمی‌تواند به عنوان یک مولفه اصلی، انتخاب شود.

Prism همچنین شامل گزینه‌هایی برای انتخاب تعداد PC خاص یا فقط نگه داشتن اولین k مولفه اصلی با بزرگترین مقادیر ویژه است (k را می توان در گزینه‌ها مشخص کرد). تصویر زیر را ببینید. به تنظیمات نرم‌افزار به هنگام انتخاب روش Select PCs based on eigenvalues مربوط می‌شود.

Select PCs based on percent of total explained variance

یکی دیگر از روش‌های رایج (کلاسیک) برای انتخاب تعداد PCها، نگه داشتن مولفه‌های اصلی با بزرگترین مقادیر ویژه است که به طور تجمعی درصد مشخصی از واریانس کل را توضیح می‌دهند. انتخاب‌های رایج برای درصد هدف از کل واریانس 75 درصد و 80 درصد است. در تصویر زیر تنظیمات این متد را ببینید.

Select all PCs

گزینه نهایی این است که Prism همه مولفه‌های اصلی را گزارش دهد. این انتخاب به ندرت مفید است، اما ممکن است برای آموزش یا اکتشاف داده‌ها مناسب باشد.

Output

تب بعدی در پنجره Parameters Principal Component Analysis (PCA) با نام Output قرار دارد. در این تب، می‌توانید خروجی‌های PCA را انتخاب کنید و جداول و گراف‌های بیشتری را برای گنجاندن در شیت نتایج تعریف کنید. در ادامه تصویر تب Output را می‌بینیم.

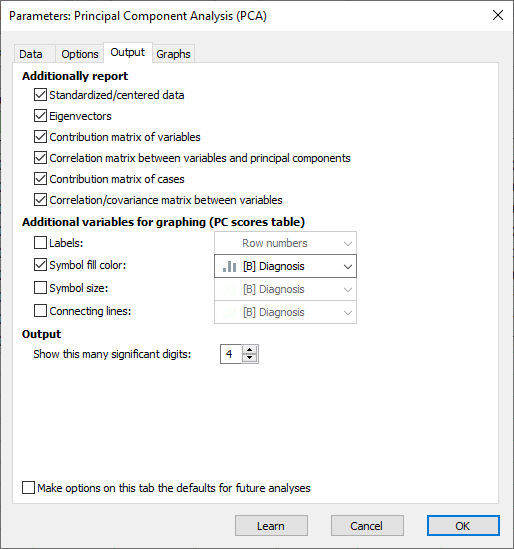
به این نکته توجه کنید که اگر ما هیچکدام از گزینه‌های بالا را هم انتخاب نکنیم، باز هم نرم‌افزار Prism، نتایج و خروجی‌های اصلی و اساسی مربوط به PCA را به ما گزارش می‌دهد. با این حال من برای آموزش بیشتر، همه گزینه‌های بالا را انتخاب کرده‌ام، در ادامه و به هنگام به دست آمدن نتایج بیشتر درباره‌ی آن‌ها صحبت می‌کنیم. در حال حاضر درباره‌ی آن‌ها مطلب بیشتری نمی‌گویم تا در خروجی‌های نرم‌افزار، جداول و نتایج مربوط به آن‌ها را ببینیم و بر روی داده‌های به دست آمده صحبت کنیم.

Graphs

در انتهای پنجره Parameters Principal Component Analysis (PCA) تب Graphs مشاهده می‌شود. تصویر زیر را ببینید.

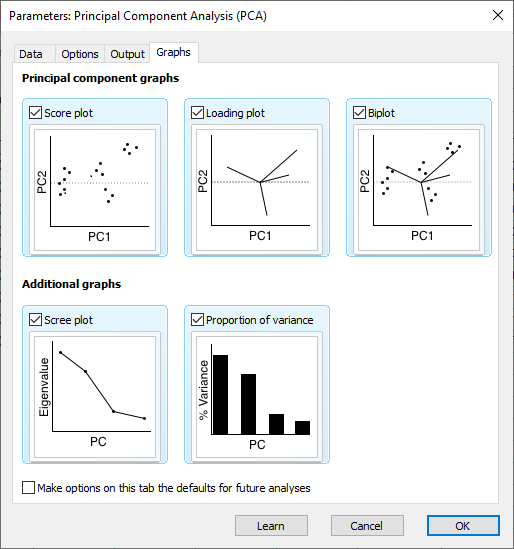
نرم‌افزار Prism، گراف‌ها و نمودارهای مختلفی به هنگام اجرا کردن PCA برای ما به دست می‌دهد. من در تنظیمات نرم‌افزار همه آن‌ها را انتخاب کرده‌ام. در ادامه و به هنگام مشاهده نمودارهای به دست آمده، درباره‌ی آن‌ها صحبت می‌کنیم.

خب، حال OK می‌کنیم. با انجام این کار در شیت‌های Results و Graphs نتایج و نمودارهای تحلیل PCA به دست می‌آید. در ادامه مقاله به توضیح و بیان آن‌ها می‌پردازیم.

نتایج تحلیل مولفه‌های اصلی در Prism

Results

پس از انجام تحلیل مولفه‌های اصلی، در شیت Results نرم‌افزار Prism، صفحه زیر را مشاهده می‌کنید.

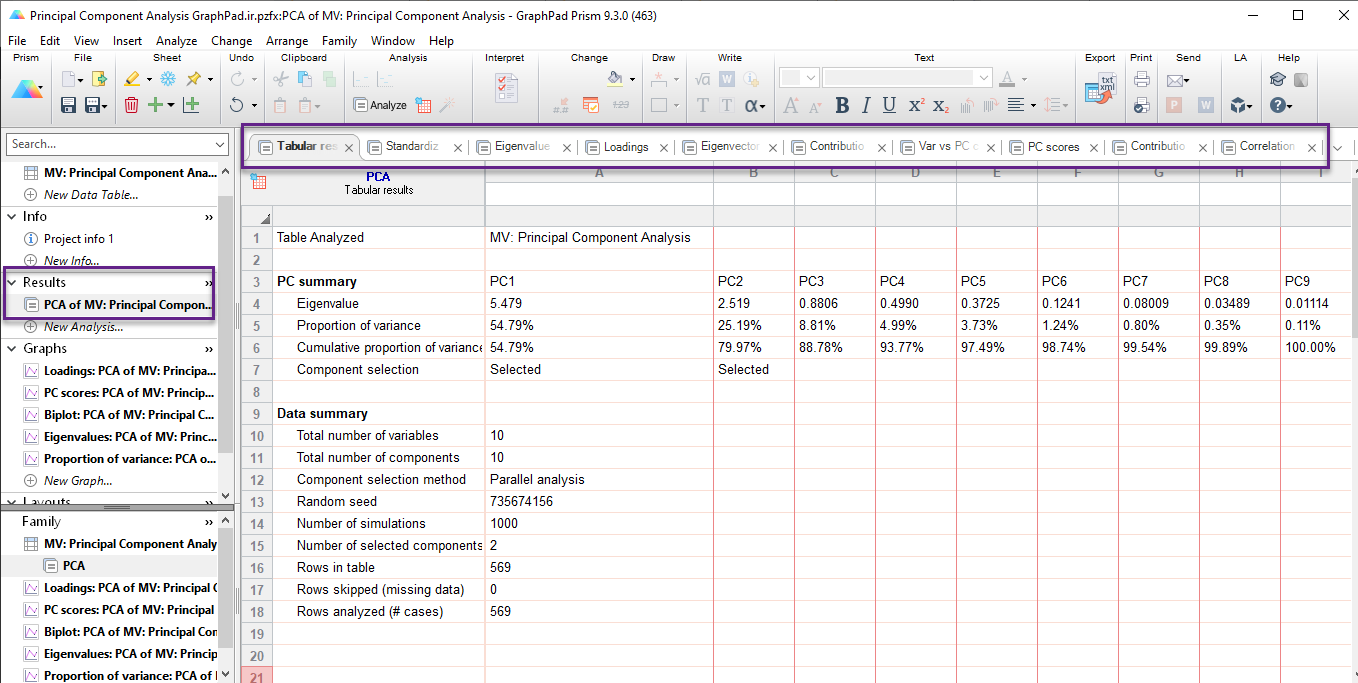
در صفحه نتایج، تب‌های مختلفی مشاهده می‌کنید. من در تصویر بالا آن‌ها را مشخص کرده‌ام. هر کدام از این تب‌ها به بیان جدول و نتایج مختلفی از تحلیل عاملی اشاره می‌کند. در ادامه هر یک را توضیح می‌دهیم.

Tabular results

اولین تبی که در شیت Results دیده می شود با نام Tabular results است. من در تصویر بالا نمای کلی از آن آورده‌ام.

در این تب اطلاعاتی درباره‌ی مولفه‌های اصلی یا همان PCهای تشکیل شده، مقادیر ویژه، نسبت واریانس توضیح داده شده (همراه با نسبت تجمعی آن)، و تعداد PCهای انتخاب شده، آمده است. من در تصویر زیر این نتایج را نشان داده‌ام.

در یک تحلیل عاملی، به تعداد Variableها، مولفه اصلی خواهیم داشت. با این حال همه آن‌ها به عنوان انتخاب شده، در تحلیل ما قرار نمی‌گیرند. در این مثال دو مولفه (PC1 و PC2) قادر به بیان 79.97 درصد پراکندگی و واریانس داده‌ها است. PC1 به تنهایی 54.79 درصد و PC2 به تنهایی 25.19 درصد واریانس داده‌ها را بیان می‌کنند.

بنابراین نتیجه می‌شود که 10 کمیت به 2 مولفه اصلی یا PC تبدیل می شوند. این همان هدف اصلی تحلیل عاملی است. یعنی تبدیل تعداد زیاد Variableها به تعداد کمتر PCها، در عین حفظ حداکثری اطلاعات (حدود 80 درصد در این مثال).

در بخش دیگر تب Tabular results، اطلاعاتی درباره تعداد کمیت‌ها، مشاهدات، روش انتخاب مولفه‌ها و موارد دیگر آمده است. در تصویر زیر آن‌ها را ببینید.

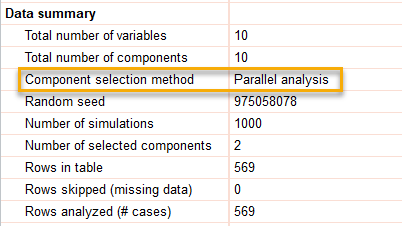
اطلاعات بیشتر Data summary در تب Tabular results

نتایج این بخش نشان می‌دهد ما تعداد 10 کمیت و مولفه داشته‌ایم. همان‌گونه که در تنظیمات نرم‌افزار انتخاب کردیم از روش تحلیل موازی Parallel analysis جهت انتخاب مولفه‌ها استفاده کرده‌ایم. در روش تحلیل موازی، 1000 مجموعه دیتا شبیه‌سازی شده و از بین 10 مولفه، 2 مولفه انتخاب شده است. تعداد مشاهدات و افراد جهت آنالیز نیز 569 فرد بوده است. داده گمشده و Missing data هم نداشته‌ایم. این خلاصه موضوعاتی است که در تحلیل عاملی مثال ما و در بخش با نام Data summary آمده است.

Standardized data

یادتان باشد در تنظیمات نرم‌افزار پنجره Parameters Principal Component Analysis (PCA) و در تب Options روش Standardized Data جهت تحلیل عاملی را انتخاب کردیم. به این معنا که از نرم‌افزار خواستیم بر روی داده‌های استاندارد شده، آنالیز انجام دهد. علاوه بر آن در تب Output نیز از نرم‌افزار خواستیم نتایج مربوط به داده‌های استاندارد شده را به ما نشان دهد. این کار در تب Standardized data انجام شده است.

در تصویر زیر می‌توانید نتایج داده‌های استاندارد شده را مشاهده کنید.

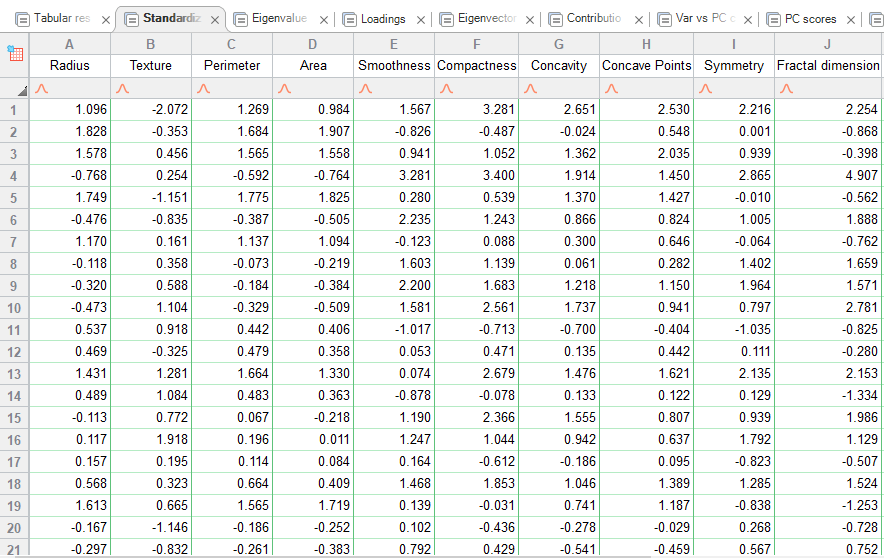
در این تب، هر ستون (Variable) از داده‌ها، استاندارد شده است. تحلیل عاملی بر روی این داده‌ها به جای داده‌های اصلی انجام می‌شود.

Eigenvalue

در این تب مقادیر ویژه Eigenvalue مربوط به هر PC آمده است. هم مقادیر ویژه مربوط به داده‌های مورد تحلیل قرار گرفته (استاندارد شده) و هم مقادیر ویژه به دست آمده از روش شبیه‌سازی و تحلیل موازی. در تصویر زیر آن‌ها را ببینید.

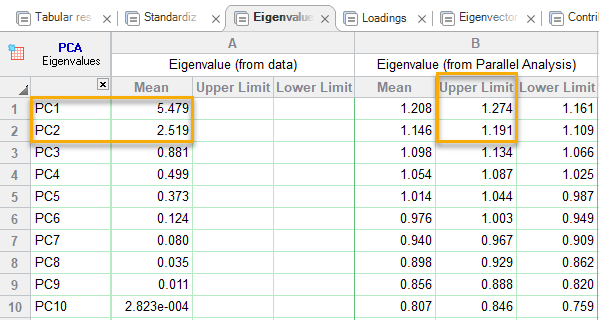
در تب بالا و در بخش مربوط به Eigenvalue (from data)، مقادیر ویژه هر PC آمده است. این نتایج از تحلیل عاملی بر روی داده‌های استاندارد شده حاصل می‌شود.

در بخش Eigenvalue (from Parallel Analysis)، مقادیر ویژه به دست آمده از تحلیل‌های عاملی بر روی داده‌های شبیه‌سازی شده (1000 مجموعه دیتا توسط نرم‌افزار ساخته شده است.) مشاهده می شود.

به ازای هر PC، میانگین، Upper Limit که همان صدک 95 ام، 1000 مقدار ویژه به دست آمده از شبیه‌سازی است، همراه با Lower Limit که صدک 5 ام، مقادیر ویژه است، دیده می‌شود.

به یاد داشته باشید، در روش تحلیل موازی بیان کردیم که مولفه‌هایی انتخاب می‌شوند که مقادیر ویژه آنها از صدک 95‌ام بزرگتر باشد. همان‌گونه که در نتایج جدول بالا مشاهده می‌کنید، صدک 95 ام برای PC1 و PC2 به ترتیب برابر با 1.274 و 1.191 به دست آمده است. این در حالی است که مقادیر ویژه به دست آمده از روی داده‌های استاندارد شده برای PC1 و PC2 به ترتیب برابر با 5.479 و 2.519 است. بنابراین مقدار ویژه این PCها از مقدار ویژه صدک 95، بزرگتر است و آن‌ها انتخاب می‌شوند.

مقدار ویژه PC3 را نگاه کنید. 0.881 شده است. از آن‌جا که این عدد از صدک 95 ام کوچکتر است، بنابراین آن را انتخاب نمی‌کنیم.

Loadings

تب بعدی در شیت نتایج نرم‌افزار Prism، با نام Loadings معرفی می‌شود. فهم نتایج این شیت ساده است. ابتدا در تصویر زیر آن را ببینید.

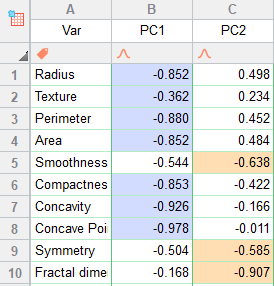
خوب است ابتدا بدانید اعداد نوشته شده، همبستگی Correlation هستند. بنابراین در بازه 1+ تا 1- قرار دارند. هر عدد نشان‌دهنده ارتباط بین Variable با PC انتخاب شده است. به عنوان مثال عدد 0.852- بیانگر وجود ارتباط قوی و وارون بین Radius و PC1 است.

کاربرد نتایج تب Loadings در این جهت است که ما می‌توانیم تشخیص دهیم، هر Variable در کدام PC بهتر است قرار گیرد. به عنوان مثال برای Perimeter عدد جدول Loadings برای PC1 و PC2 به ترتیب برابر با 0.880- و 0.452 به دست آمده است. این اعداد نشان می‌دهند Perimeter بیشتر تمایل دارد به PC1 تعلق گیرد، زیرا دارای همبستگی قوی‌تری با آن است.

به همین ترتیب برای سایر Variableها، در هر PC که عدد آن بزرگتر بود (به صورت قدرمطلق و صرفنظر از مثبت یا منفی بودن آن)، به همان PC تعلق می‌گیرد. من در جدول بالا با استفاده از رنگ، مشخص کردم که هر Variable متعلق به کدام PC است.

Eigenvectors

بردارهای ویژه Eigenvectors که به آن‌ها بردارهای مولفه اصلی Principal Component Vectors نیز می‌گویند، بیانگر ضرایب مدل خطی بین PCها با Variableها هستند. در تصویر زیر من جدول بردارهای ویژه برای مولفه‌های اصلی انتخاب شده را آورده‌ام.

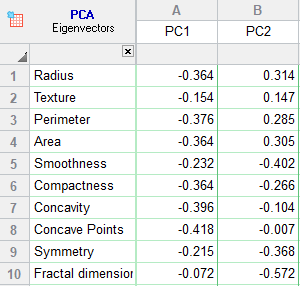
به عنوان مثال مدل‌های زیر را ببینید.

$\small PC1 \; is \; defined \; as = -0.364 \times Radius - 0.154 \times Texture - 0.376 \times Perimeter \; and \; so \; on$

$\small PC2 \; is \; defined \; as = 0.314 \times Radius + 0.147 \times Texture + 0.285 \times Perimeter \; and \; so \; on$

از آن‌جا که می‌توان بردارهای ویژه را به عنوان ضرایب رگرسیونی در نظر گرفت، بنابراین عدد بزرگتر مقدار ویژه به معنای تاثیر بیشتر آن Variable بر PC است. به این نکته دقت کنید که نتیجه‌ای که تب Loadings در تعلق Variable به PC به دست می‌دهد همانند نتایج تب Eigenvectors است.

Contribution of variables

تب بعدی با نام Contribution of variables دیده می‌شود. در تصویر زیر می‌توانید آن را ببینید.

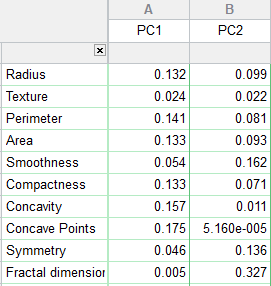
اعداد نوشته شده روبه‌روی هر Variable، درصدی از واریانس کل است که توسط آن PC توضیح داده شده است. بنابراین هر چقدر عدد بزرگتر باشد به معنای آن است که کمیت، پراکندگی بیشتری از PC را به خود اختصاص می‌دهد.

چنانچه دقت کنید، مجموع اعداد نوشته شده در هر ستون برابر با یک می‌شود. نتیجه به دست آمده از این تب، همانند نتایج تب‌های Loadings و Eigenvectors است.

خوب است این نکته را هم بدانید که از نظر عددی، مقادیر جدول Contribution of variables، مجذور مقادیر مربوطه در جدول بردارهای ویژه هستند.

Var vs PC Correlation

چنانچه دقت کنید، نتایج این تب همانند جدول Loadings است. بنابراین اعداد آن را می‌توان به عنوان همبستگی بین هر Variable با PC در نظر گرفت.

PC scores

به منظور درک نتایج این تب، بهتر است یکبار دیگر نتایج تب Eigenvector را ببینید. من در آن‌جا از یک مدل خطی رگرسیونی صحبت کردیم که در آن PCها، کمیت وابسته Dependent Variable (DV) و Eigenvectorها ضرایب مدل رگرسیونی بودند.

آنچه در این تب و در تصویر زیر مشاهده می‌کنید، در واقع همان DVهای برازش شده برای هر فرد، در مدل رگرسیونی است که ما به آن PC Score می‌گوییم. آن‌ها را ببینید.

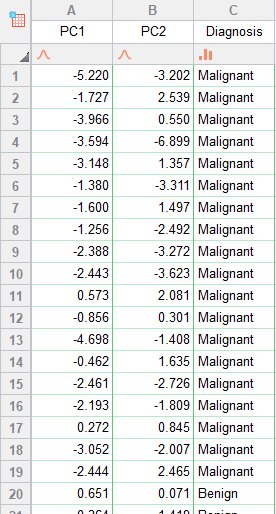
اعداد نوشته شده در ستون‌های PC1 و PC2، مقدار برازش شده برای مدل رگرسیون خطی است که در آن Variableها همان Independent Variable (IV) هستند. در ستون Diagnosis نیز تشخیص خوش‌خیم یا بدخیم بودن بافت سرطانی را مشاهده کنید.

چنانچه علاقمند باشیم از نتایج این شیت می‌توانیم در یک تحلیل رگرسیون لجستیک که در آن Diagnosis به عنوان کمیت وابسته (به صورت خوش خیم و بدخیم با کدهای صفر و یک) و PCها به عنوان کمیت‌های مستقل Independent Variable مطرح هستند، استفاده کرد.

Contribution of cases

به یاد داشته باشید در نتایج تب Contribution of variables بیان کردیم که اعداد نوشته شده روبه‌روی هر Variable، درصدی از واریانس کل است که توسط آن PC توضیح داده شده است. حال اینجا بیان می‌کنیم که اعداد نوشته شده در تب Contribution of cases، درصدی از واریانس کل است که در هر PC توسط هر فرد، بیان می‌شود.

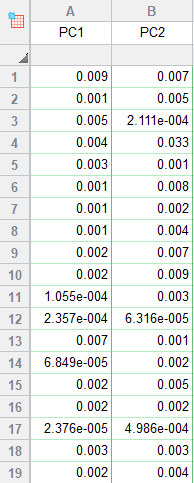
نکته‌ای که در این جدول وجود دارد این است که با استفاده از نتایج آن می‌توانیم به شناسایی داده‌های پرت یا غیرمعمول Outliers or Unusual، استفاده کنیم. به عنوان مثال، تصویر زیر را ببینید.

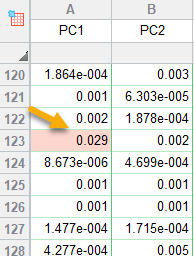
شناسایی داده‌های پرت در جدول Contribution of cases

در ردیف شماره 123، یک نتیجه غیرمعمول به دست آمده است که بیانگر پرت بودن این Case است. در این ردیف، Case شماره 123 به تنهایی 2.9 درصد واریانس PC1 را بیان می‌کند. این عدد نسبت به سایر caseها که تعداد آن‌ها 569 مورد است، زیاد به نظر می‌رسد.

Correlation matrix

نتایج جدول Correlation matrix به بیان همبستگی بین Variableهای مطالعه با یکدیگر می‌پردازد. در تصویر زیر آن را ببینید.

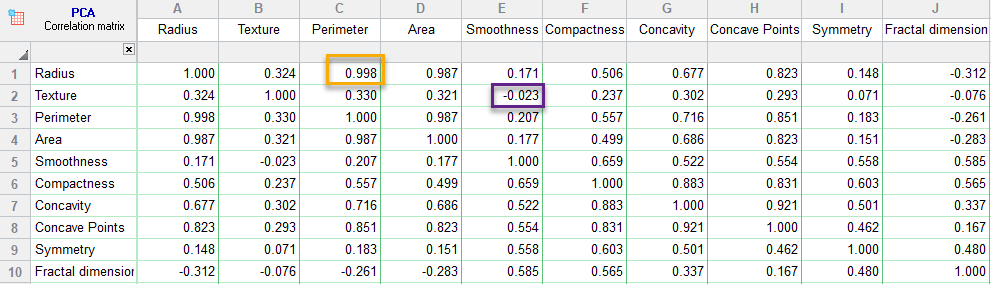
به عنوان مثال نتایج این جدول نشان می‌دهد، ارتباط بین کمیت‌های Radius و Perimeter مثبت و قوی (r = 0.998) و ارتباط بین Texture و Smoothness ضعیف و بی‌معنا است (r = -0.023).

به این ترتیب ما تا اینجا توانستیم به بیان و توضیح جداول و نتایج به دست آمده از تحلیل مولفه‌های اصلی در شیت Results بپردازیم.

در ادامه کار به توضیح و مشاهده نمودارها و گراف‌های نتیجه شده از PCA خواهیم پرداخت.

گراف‌های تحلیل مولفه‌های اصلی

Graphs

در یک تحلیل عاملی با استفاده از نرم‌افزار Prism، گراف‌ها و نمودارهای متنوعی به دست می‌آید. در تصویر زیر، جایگاه آن‌ها را در صفحه نرم‌افزار مشاهده می‌کنید.

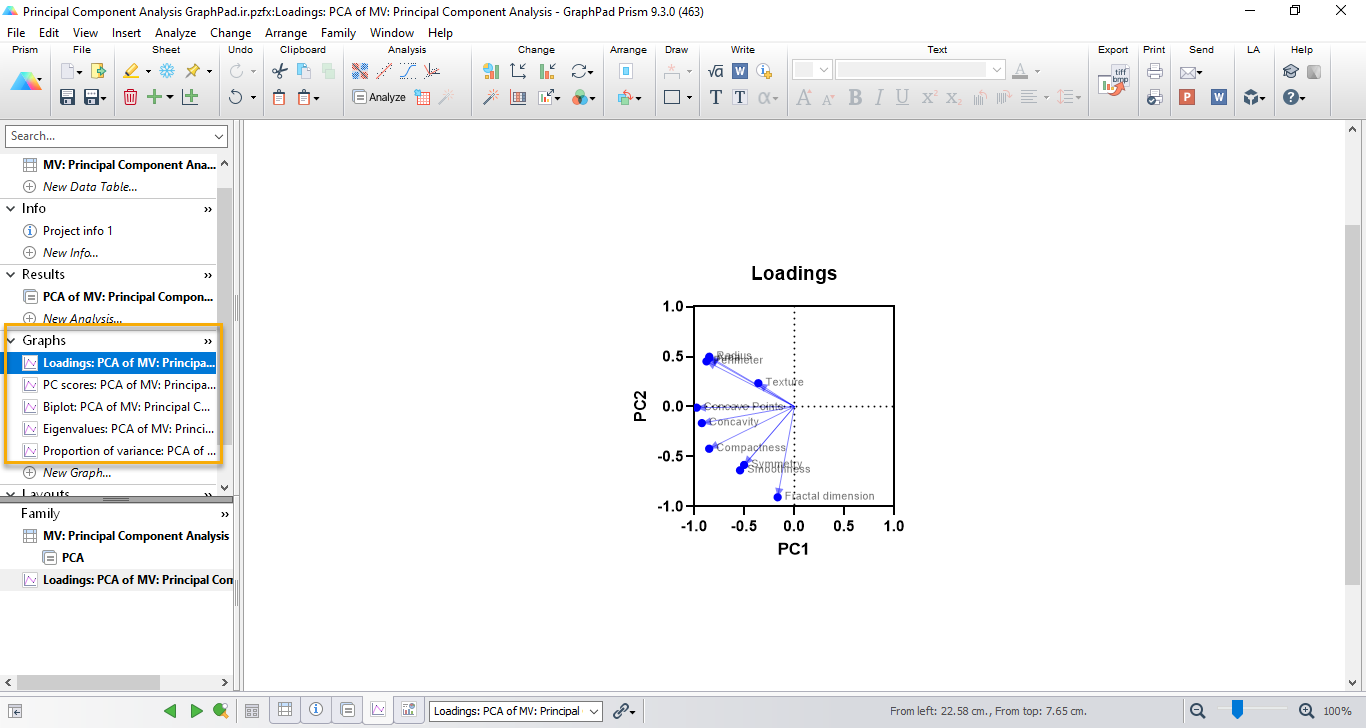
نرم‌افزار Prism در یک تحلیل عاملی، تعداد پنج نمودار و گراف برای ما رسم می‌کند.

Loadings
PC scores
Biplot
Eigenvalues
Proportion of variance

در ادامه درباره‌ی هر یک توضیح می‌دهیم. از گراف Loadings شروع می‌کنیم. در تصویر زیر آن را ببینید.

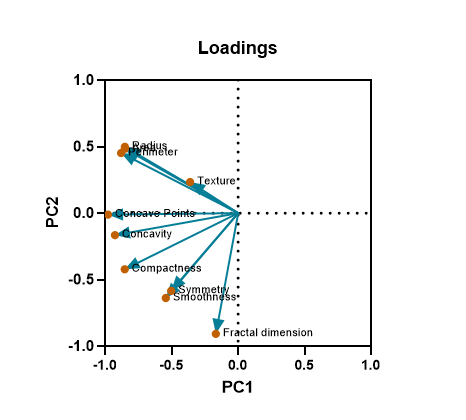
برای فهم این گراف بهتر است به شیت Results و تب Loadings بروید. در آن‌جا بیان کردیم که همبستگی بین هر کدام از Variableها با PCها به دست آمده است. از آن‌جا که با دو مولفه اصلی روبه‌رو بودیم، بنابراین همبستگی هر Variable به صورت آرایه (x,y) که در آن x همبستگی کمیت با PC1 و y همبستگی با PC2 است، گزارش می‌شود.

به عنوان مثال برای Radius آرایه (0.498 ,0.852-) به دست آمده است. این آرایه نشان می‌دهد، Radius با PC1، همبستگی به اندازه 0.852- و با PC2 همبستگی 0.498 واحد دارد.

در گراف Loadings می‌توانید آرایه‌های همبستگی به ازای هر Variable را ببینید. دایره‌ها همان نقاط عددی همبستگی برای PC1 و PC2 هستند. خطوط نیز از مبدا مختصات و از نقطه (0 ,0) رسم شده‌اند. قبلاً نیز بیان کردیم همبستگی کمیت با هر کدام از PCها که بیشتر باشد، به آن PC اختصاص داده می‌شود.

کاربرد دیگر گراف Loadings در این است که می‌توانیم به رابطه بین Variableها با یکدیگر نیز پی ببریم. همانطور که در نمودار بالا نشان داده شده است، Radius، perimeter و Area به صورت خوشه‌ای نزدیک به هم هستند که نشان می‌دهد آن‌ها دارای همبستگی مثبت با یکدیگر هستند. در مقایسه، بردارهای Texture و Symmetry یا بردارهای Texture و Symmetry یک زاویه تقریباً قائم را تشکیل می‌دهند که نشان می‌دهد با یکدیگر همبستگی ندارند. با بازگشت به نتایج تب Correlation matrix، می‌توانیم تایید کنیم که این فرضیات تا حد زیادی درست هستند.

گراف بعدی نرم‌افزار Prism، با نام PC Scores دیده می‌شود. در تصویر زیر آن را آورده‌ام.

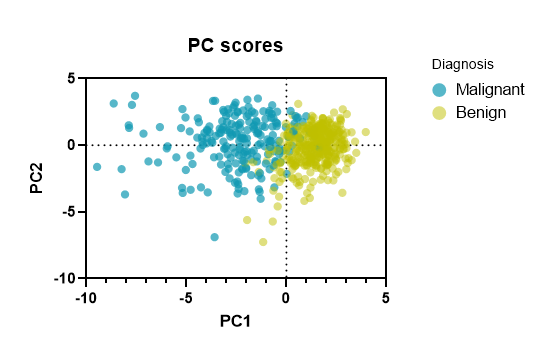
معمولاً گراف‌ها در نرم‌افزار Prism، بیانگر نتایج به دست آمده و درکی شهودی از آن‌ها هستند. گراف PC Scores نیز نتایج تب PC Scores در شیت نتایج را نشان می‌دهد. به منظور اختصار، می‌توانید به توضیحات بیان شده در تب PC Scores مراجعه کنید.

نکته‌ای که در این گراف وجود دارد این است که به ازای هر کدام از تشخیص‌ها (بدخیم و خوش‌خیم) نتایج جداگانه رسم شده است. هر دایره نیز یک فرد و ردیف در شیت دیتا را نشان می‌دهد. این گراف نشان می‌دهد افرادی که تشخیص توده سرطانی در آن‌ها خوش‌خیم (Benign) بوده است، دارای PC scoreهای متمرکزتری نسبت به افراد با تشخیص بدخیم (Malignant) می‌باشند.

از گراف PC Score می‌توانیم جهت شناسایی داده‌های پرت یا غیرمعمول Outliers or Unusual، مطالعه نیز استفاده کنیم. این مطلب را در توضیحات تب Contribution of cases، که درصد از واریانس کل بیان شده توسط هر فرد، است بیان کردیم. در واقع داده‌هایی که دورتر از سایر افراد در گراف PC Score قرار می‌گیرند، به عنوان افرادی که حجم و درصد زیادی از واریانس را در بر می‌گیرند، گزارش می‌شوند. در تصویر زیر می‌توانید برخی از آن‌ها را ببینید.

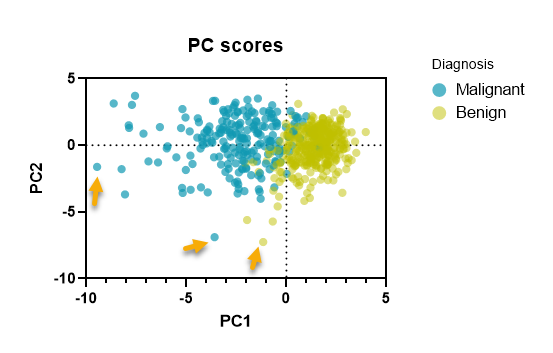
چنانچه موس را بر روی دایره‌های مشخص شده در بالا ببرید، می‌توانید شماره ردیف آن‌ها را در شیت دیتا مشاهده کنید.

گراف بعدی تحلیل مولفه‌های اصلی با نام Biplot شناخته می‌شود. در تصویر زیر آن را ببینید.

شاید بتوان گفت Biplot چیز جدیدی نیست و از ترکیب گراف‌های بالا یعنی Loadings و PC scores به دست می‌آید. به هر حال اگر علاقمند بودید، آن‌ها را در یک نمودار و کنار هم ببینید، می‌توانید از Biplotها استفاده کنید.

گراف دیگر به دست آمده از تحلیل مولفه های اصلی در نرم‌افزار Prism، با نام Eigenvalue خوانده می‌شود. این نمودار در نرم‌افزاری مانند SPSS به نام Scree Plot گفته می‌شود. در تصویر زیر آن را ببینید.

توضیحات مربوط به این گراف را می‌توانید در تب Eigenvalues از شیت Results، مشاهده کنید. مقادیر ویژه (که بیانگر درصد بیان کننده از واریانس کل است)، به ازای هر PC آمده است. مقادیر ویژه در نمودار بالا هم به ازای داده‌های اصلی (استاندارد شده) و هم به ازای تحلیل موازی (مجموعه داده‌های شبیه‌سازی شده)، رسم شده است.

همان‌گونه که مشاهده می‌کنید، صرفاً PCهای شماره 1 و 2 دارای مقادیر ویژه بزرگتر از Parallel Analysis هستند. بنابراین فقط همین PC ها را انتخاب می‌کنیم.

در نهایت هنگام انجام تحلیل عاملی با نرم‌افزار Prism، گراف دیگری با نام Proportion of variance آمده است. این نمودار به واریانس توضیح داده شده توسط هر PC اشاره می‌کند. در تصویر زیر آن را می‌بینید.

گراف Proportion of variance در تحلیل عاملی

نتایج این گراف را می‌توانید در تب Tabular results ببینید. در نمودار Proportion of variance، خط به معنای واریانس بیان شده توسط هر PC است. همواره این خط نزولی است و می‌توان آن را شِمای دیگری از گراف Eigenvalues دانست. با افزایش تعداد PCها، واریانس بیان شده توسط هر کدام، کاهش می‌یابد. به همین دلیل ما فقط دو یا سه PC ابتدایی را انتخاب می‌کنیم.

همچنین در نمودار بالا، ستون‌ها به معنای واریانس تجمعی توضیح داده شده توسط مولفه‌های اصلی هستند. به سادگی می‌دانیم روند آن‌ها صعودی است و در انتها به عدد 100 می‌رسند. این گراف نشان می‌دهد PC1 و PC2 روی هم، حدود 80 درصد پراکندگی و واریانس داده‌ها را توضیح می‌دهند که عدد مناسبی است.

در این مقاله به موضوع تحلیل مولفه های اصلی یا همان تحلیل عاملی (PCA) Principal Component Analysis در نرم‌افزار GraphPad Prism پرداختیم. جداول و نمودارهای به دست آمده را بیان کرده و هر یک را توضیح دادیم. ما معمولا‍ً از نرم‌افزارهایی مانند SPSS جهت تحلیل عاملی استفاده می‌کنیم، با این حال در این مقاله توصیه می‌کنیم که کاربرد Prism در انجام PCA را نیز یاد بگیرید که می‌تواند راهنمای خوبی برای ما باشد.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2022). Principal Component Analysis (PCA) in Prism software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/principal-component-analysis-prism/.php

For example, if you viewed this guide on 12^th January 2022, you would use the following reference

GraphPad Statistics (2022). Principal Component Analysis (PCA) in Prism software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/principal-component-analysis-prism/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.

سبد خرید