عدم برازش Lack of Fit مدل با استفاده از نرم افزار Minitab

زمان مطالعه: 10 دقیقه 

هنگامی که یک مدل رگرسیونی با استفاده از نرم‌افزار Minitab برازش می‌دهیم در نتایج آزمونی با نام Lack of Fit دیده می‌شود.

در این متن می‌خواهیم به این مفهوم بپردازیم. البته از این لینک نیز می‌توانید توضیحات هلپ نرم افزار Minitab را نیز مشاهده کنید.

در توضیح Lack of Fit بیان می‌کنیم که ما از هر مدل رگرسیونی چه خطی و چه غیرخطی این انتظار را داریم که بتواند بین پاسخ Response و کمیت‌های مستقل Independent Variables یا فاکتورهای تجربی Experimental Factors یک ارتباط خوب و منطقی به دست بیاورد.

حال اگر به هر دلیلی مدل مناسب نباشد و برازش خوبی به دست نیاید می‌گوییم Lack of Fit یا همان کمبود و عدم برازش داشته‌ایم. Lack of Fit می‌تواند به دلایلی مانند عدم قرار گرفتن اثرات متقابل Interactions و یا جملات درجه دوم Quadratic Terms در مدل رگرسیونی، رخ دهد.

دلیل دیگر رخ دادن Lack Of Fit وجود چندین باقیمانده بزرگ Large Residuals می‌باشد. در این حالت بهتر است سطرها و داده هایی را که از دیدگاه نرم افزار دارای باقیمانده بزرگ هستند از مجموعه دیتا حذف کنیم.

آزمون Lack of Fit یک فرضیه آماری است، بنابراین دارای فرض‌های صفر و جایگزین است. فرض صفر در این آزمون به معنای عدم وجود Lack of Fit است و فرض مقابل  برقراری Lack of Fit را بیان می‌کند. بنابراین یک مدل خوب رگرسیونی، مدلی است که مقدار احتمال آزمون Lack of Fit آن بیشتر از سطح معنی داری آلفا (که معمولاً پنج درصد در نظر گرفته می‌شود) باشد. یعنی فرض صفر پذیرفته شود.

در این حالت می‌توانیم بگوییم با یک مدل و برازش مناسب روبه‌رو هستیم و شواهد کاقی برای بیان وجود Lack of Fit در اختیار نداریم.

در این حالت بیان می‌کنیم که برازش مدل چندان مناسب نیست و کمبود برازش یا همان Lack of Fit رخ داده است.

حال بیایید از یک مثال استفاده کنیم. فایل مثال را می‌توانید از اینجا دریافت کنید.

در این فایل می‌خواهیم بین Computer Sales به عنوان Response و Software Sales به عنوان Continuous Predictor یک مدل رگرسیونی ایجاد کنیم.

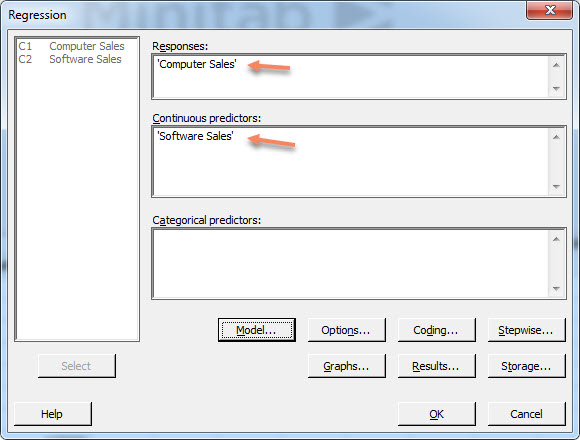
ابتدا از مسیر زیر در نرم‌افزار Minitab وارد محیط تحلیل رگرسیونی می‌شویم.

پنجره زیر برای ما باز می‌شود. ستون‌ها را همانند شکل زیر در تنظیمات قرار می‌دهیم.

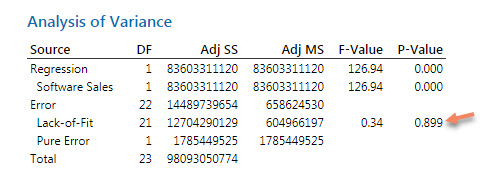
با OK کردن نتایج تحلیل رگرسیونی شامل معادله رگرسیونی، ضریب تعیین، جدول ضرایب و آنالیز واریانس برای ما به دست می‌آید.

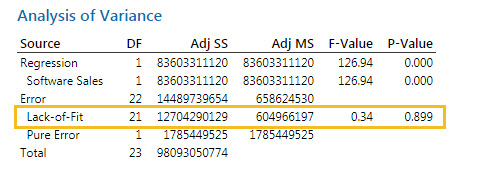
آماره Lack of Fit را می‌توان در در زیر Source با نام Error مشاهده کرد.

مقدار احتمال آن برابر با 0.899 شده است و از آن‌جا که بالاتر از آلفای پنج درصد به دست آمده بنابراین فرض صفر آزمون Lack of Fit تایید می‌شود. این فرض به معنای عدم وجود Lack of Fit و مناسب بودن مدل برازش شده است.

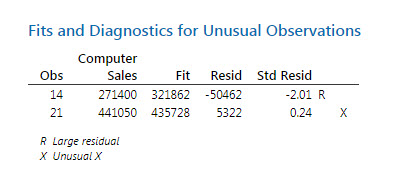
در پایین جدول Analysis of Variance جدول دیگری با نام Fits and Diagnostics for Unusual Observations دیده می‌شود. در نتایج این جدول باقیمانده‌های بزرگ و Xهای غیرمعمول (البته چنانچه در دیتا وجود داشته باشد) دیده می‌شود.

اهمیت این جدول در آن است که اگر با یک مدل دارای Lack of Fit مواجه شدید، می‌توانید با حذف سطرهای دارای باقیمانده بزرگ و یا X غیرمعمول، احتمالاً یک مدل فاقد Lack of Fit به دست بیاورید.

نکته مهم

 ستاره‌ها  در نتایج Lack of Fit

گاهی اوقات اتفاق می‌افتد که نرم‌افزار نتایج و یافته‌هایی برای Lack of Fit ارایه نمی‌کند. به تصویر زیر نگاه کنید.

دلیل اصلی این مطلب این است که ستاره ها مقادیر از دست رفته‌ای را نشان می دهند که قابل محاسبه نیستند زیرا مدل اشباع شده است و درجه آزادی کافی برای خطا وجود ندارد.

این اتفاق به دلایلی از جمله تعداد کم نمونه در مطالعه و یا زیاد بودن تعداد Xهای مدل، رخ می‌دهد. به بیان ساده‌تر یعنی این‌که تعداد نمونه کافی در مطالعه وجود ندارد. برای حل این مشکل کافی است تعداد نمونه‌ها را افزایش دهید. یا این‌که تعداد Xهای مدل را کاهش دهیم.