نسبت خطر Hazard Ratio در آنالیز بقا چیست؟
Hazard Ratio
نسبت خطر معمولاً هنگام ارایه نتایج کارآزماییهای بالینی شامل دادههای بقا استفاده میشود و امکان آزمایش فرضیههای تحلیل بقا را فراهم میکند. Hazard، فراوانی رویداد مورد علاقه در واحد زمان را بیان میکند و میتوان آن را به عنوان “شیب” Slope منحنی بقا در نظر گرفت. این معیاری است که نشان میدهد آزمودنیها با چه سرعتی رویداد مورد علاقه را تجربه میکنند.
نسبت خطر یا همان Hazard Ratio مقایسه خطر Hazard بین دو گروه است. به عنوان مثال اگر نسبت خطر 2.0 باشد، آنگاه نرخ رویدادی که در یک گروه رخ میدهد دو برابر نرخ رویداد در گروه دیگر است.
به این نکته توجه کنید که نسبت خطر در هیچ نقطه زمانی واحدی محاسبه نمیشود، بلکه از روی تمام دادههای موجود در منحنی بقا محاسبه میشود.
از آنجایی که فقط یک نسبت خطر گزارش میشود، تنها در صورتی میتوان آن را تفسیر کرد که فرض کنید نرخ خطر جمعیت population hazard rate در طول زمان ثابت است و هر گونه تفاوت به دلیل نمونه گیری تصادفی است. این فرض خطرات متناسب proportional hazards نامیده میشود و یک فرض اساسی در رگرسیون خطرات متناسب کاکس Cox proportional hazards regression است. در این زمینه علاقمند بودید لینک (باقیمانده ها Residuals در رگرسیون خطرات متناسب کاکس) را بخوانید.
اگر نرخ خطر در طول زمان ثابت نباشد، عددی که نرمافزار Prism برای نسبت خطر گزارش میکند مفید نخواهد بود. اگر دو منحنی بقا با هم برخورد و تلاقی کنند، نرخهای خطر ثابت نیستند. یک استثنا در این مورد است که منحنیها در زمانهای پایانی متقاطع شوند، یعنی زمانی که تعداد کمی از آزمودنیها هنوز در مطالعه وجود دارند.
نسبت خطر Hazard Ratio ارتباط مستقیمی با میانه بقا Median Survival ندارد. مثلاً نسبت خطر 2.0 به این معنی نیست که میانه بقا در یک گروه دو برابر میانه بقا در گروه دیگر است. بلکه نسبت خطر 2.0 به این معنی است که یک آزمودنی در یک گروه که رویداد مورد علاقه را در یک نقطه زمانی معین تجربه نکرده است، در مقایسه با یک آزمودنی در گروه دیگر، دو برابر احتمال دارد که آن رویداد را تا نقطه زمانی بعدی تجربه کرده باشد.
نرمافزار پریسم نسبت خطر – و فاصله اطمینان آن – را با استفاده از دو روش محاسبه میکند که در زیر توضیح داده شده است. برای هر روش، Prism هم نسبت خطر و هم وارون آن را گزارش میکند. اگر آزمودنیهای گروه A رویداد مورد علاقه را با دو برابر نرخ آزمودنیهای گروه B (یعنی HR=2.0) تجربه کنند، آزمودنیهای گروه B – طبق تعریف – رویداد مورد علاقه را با نصف نرخ آزمودنیهای گروه A تجربه خواهند کرد. (HR=1/2.0=0.5)
در زمینه Hazard Ratio و تعاریف و توضیحات آن علاقمند بودید به دو مقاله زیر مراجعه کنید.
-
- Hazards of Hazard Ratios (M.A. Hernán. Epidemiology. 21:13-5, 2010).
- Hazard ratio in clinical trials. ( Spruance et al, Antimicrobial Agents and Chemotherapy vol. 48 (8) pp. 2787, 2004).
- روشهای محاسبه Hazard Ratio در Prism
Prism نسبت خطر را با دو روش مختلف گزارش میدهد، Logrank و Mantel-Haenszel. این دو روش معمولاً نتایج یکسان (یا تقریباً یکسان) ارایه میدهند. با این حال، هنگامی که چندین آزمودنی، رویداد مورد علاقه را به طور همزمان تجربه میکنند (در اصطلاح به آنها “مشاهدات گره خورده” Tied Observations گفته میشود) یا هنگامی که نسبت خطر از عدد 1.0 فاصله زیادی دارد، نتایج میتواند متفاوت باشد.
برنشتاین و همکارانش در مقاله زیر
L Bernstein, J. Anderson and MC Pike. Estimation of the proportional hazard in two-treatment-group clinical trials. Biometrics (1981) vol. 37 (3) pp. 513-519
دادههای شبیهسازی شده را با هر دو روش Logrank و Mantel-Haenszel تحلیل کردند. در تمام شبیهسازی های آنها، پیشفرض خطرات متناسب proportional hazards برقرار بود. دو روش مقادیر بسیار مشابهی برای نسبت خطر تولید کردند. روش Logrank (که از آن به عنوان روش O/E نیز یاد میکنند) مقادیر نزدیک به نسبت خطر واقعی را گزارش میکند، به ویژه زمانی که نسبت خطر عددی بزرگ یا حجم نمونه مطالعه زیاد است.
هنگامی که مشاهدات گره خورده وجود دارد، هر دو روش دقت کمتری دارند. روش Logrank تمایل دارد نسبتهای خطر را نزدیکتر به 1.0 گزارش کند. بنابراین، نسبت خطر گزارش شده هنگامی که بیشتر از 1.0 بیان میشود، نسبت به مقدار واقعی آن کوچک است، و وقتی کمتر از 1.0 گزارش میشود، نسبت به مقدار واقعی آن بزرگ است). در مقابل، روش Mantel-Haenszel نسبتهای خطر را بیشتر از 1.0 گزارش میکند (بنابراین نسبت خطر گزارش شده زمانی که بیشتر از 1.0 گزارش میشود بزرگ است، و زمانی که کمتر از 1.0 گزارش میشود کوچک است.
سوال. وقتی نسبت خطر بر مبنای روشهای بالا، با یکدیگر متفاوت هستند به چه معناست؟
شبیهسازیهای برنشتاین و همکاران این دو روش را با دادههای شبیهسازیشده در جایی که فرض خطرات متناسب برقرار نبود، مقایسه نکردند. در مثال جداگانهای که آن را میتوانید از این لینک دریافت کنید از دادههایی که در آنها فرض خطرات متناسب برقرار نبود، استفاده شد. نتیجه به دست آمده بیان میکرد که نسبت خطر بین دو روش بسیار متفاوت است.
در تصویر زیر نتایج نسبت بخت Hazard Ratio برای این مثال آمده است. این همان مثالی است که گفتم در آن پیشفرض خطرات متناسب برقرار نیست و در نتیجه عدد نسبت بخت به دست آمده بر مبنای روشهای Logrank و Mantel-Haenszel با یکدیگر متفاوت است.
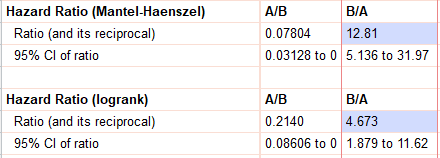
منحنی بقا برای این مثال را نیز میتوانید در شکل زیر ببینید.
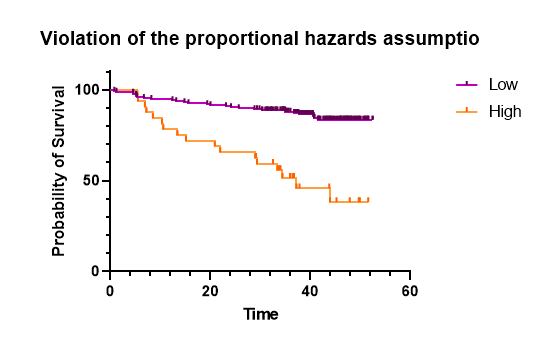
به نظر میرسد که روش Mantel-Haenszel به تفاوت در نرخ خطر در زمانهای انتهایی مطالعه، وزن بیشتری میدهد، در حالی که روش logrank به همه نقاط زمانی وزن یکسان میدهد.
بنابراین نکته مهم این است که اگر مقادیر نسبت خطر بسیار متفاوتی را با این دو روش مشاهده کردید، نتیجه میشود پیشفرض خطرات متناسب برقرار نیست پس مفهوم یک نسبت خطر واحد که کل منحنی بقا را توصیف میکند، معنادار نیست و نمیتوان عدد به دست آمده برای HR را صحیح دانست.
چنانچه به نحوه محاسبه و فرمولهای آماری روشهای Logrank و Mantel-Haenszel علاقمند بودید، این لینک و یا این لینک را ببینید. در فصل سوم کتاب زیر نیز جزئیات محاسبه نسبت بخت توسط این روشها به تفصیل بیان شده است. علاقمند بودید آن را ببینید.
David Machin, Yin Bun Cheung, Mahesh Parmar, Survival Analysis: A Practical Approach, 2nd edition, IBSN:0470870400
- مثال. یک مثال عددی ببینیم (Example)
هنگامی که با نرمافزار Prism آنالیز بقا کاپلان مایر را انجام میدهیم و به مقایسه منحنیهای بقا بین دو گروه (به عنوان مثال گروههای درمان و کنترل) میپردازیم، در شیت نتایج Curve comparison خروجیهایی با عنوان Hazard Ratio به دست میآید. در تصویر زیر آنها را ببینید. علاقمند بودید توضیحات بیشتری دربارهی کاپلان مایر بدانید لینک (تحلیل کاپلان مایر Kaplan-Meier آنالیز بقا با نرمافزار Prism) را مشاهده کنید.
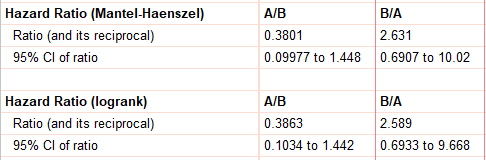
همانگونه که در جدول بالا میبینید نسبت خطر همراه با فواصل اطمینان 95% با استفاده از روشهای Logrank و Mantel-Haenszel به دست آمده است. به عنوان مثال نتیجه به دست آمده نشان میدهد نرخ رویداد (مرگ) در گروه B حدود 2.6 برابر نرخ رویداد در گروه A است $ \displaystyle \left( {H{{R}_{{B/A}}}=2.631} \right)$.
نسبت خطر 2.6 به این معنی است که آزمودنی گروه B که هنوز مرگ را در یک نقطه زمانی تجربه نکرده، در مقایسه با آزمودنی گروه A، حدود 2.6 برابر احتمال دارد که آن مرگ را تا نقطه زمانی بعدی تجربه کند. این مطلب همان شیب منحنی بقا را نشان میکند و به عبارتی بیان میکند سرعت آزمودنیهای گروه B حدود 2.6 برابر آزمودنیها گروه A جهت تجربه رویداد مورد بررسی است.
- نسبت خطر به صورت A/B یعنی گروه A در مقایسه با گروه B و همچنین وارون آن، B/A یعنی گروه B در مقایسه با گروه A، براورد میشود.
- نزدیک بودن اعداد براورد شده برای نسبت بخت به یکدیگر بر مبنای روشهای Logrank و Mantel-Haenszel، نشاندهنده برقرار بودن پیشفرض خطرات متناسب proportional hazards در دادههای مورد بررسی است.
- فواصل اطمینان براورد شده، همگی عدد 1.0 را دربردارند. این یافته به ظاهر ساده نشان میدهد که اختلاف معناداری بین احتمال بقا در گروههای A و B وجود ندارد. به عبارت دیگر زمان بقا در این گروهها با هم تفاوت معنادار آماری ندارند. این نتیجه را میتوان با استفاده از آزمون کاپلان مایر نیز به دست آورد و P value آن را مشاهده کرد.
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2023). What is the Hazard Ratio?. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/hazard-ratio/.php
For example, if you viewed this guide on 12th January 2023, you would use the following reference
GraphPad Statistics (2023). What is the Hazard Ratio?. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/hazard-ratio/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.


