اندازه اثر Effect Size در تحلیلهای مقایسه میانگین با استفاده از نرمافزار SPSS
Effect Size in Compare Mean Tests
هنگامی که به مقایسه میانگین یک گروه با یک عدد ثابت و یا مقایسه میانگین دو یا چند گروه با یکدیگر میپردازیم، به سادگی میتوانیم از آزمونهای مقایسه میانگین Compare Mean استفاده کنیم.
این آزمونها روشهایی مانند
-
- One-Sample T Test
- Independent Sample T Test
- Paired Sample T Test
- One-way ANOVA
و در ابعادی گستردهتر تحلیلهایی LM و یا GLM مانند آنالیز واریانس، کوواریانس، تحلیلهای Univariate و Multivariate میباشند.
نکتهای که در انجام این تحلیلها وجود دارد این است که این آزمونها به ما وجود یا عدم وجود اختلاف معنادار و تفاوت بین گروهها را بیان میکنند اما چیزی درباره اندازه تفاوت، نمیگویند. از این رو مفهومی به نام اندازه اثر Effect Size که به بیان اندازه اختلاف و تفاوت بین گروهها میپردازد، حائز اهمیت است.
من در این مقاله به دنبال این هستم که با توجه به طرح تحقیقاتی و مطالعهای که انجام میدهیم و همچنین آزمونی که بر روی دادهها، تحلیل میکنیم، به محاسبه اندازه اثر بین اختلافها و گروهها، بپردازم. در واقع محاسبه و یافتن اندازه اثر بر مبنای نوع آزمونی که انجام میدهیم، میباشد. در ادامه چند مثال را با یکدیگر مشاهده میکنیم. این کار را با استفاده از نرمافزار SPSS انجام خواهیم داد. فایل دیتا این مقاله را میتوانید از اینجا دریافت کنید.
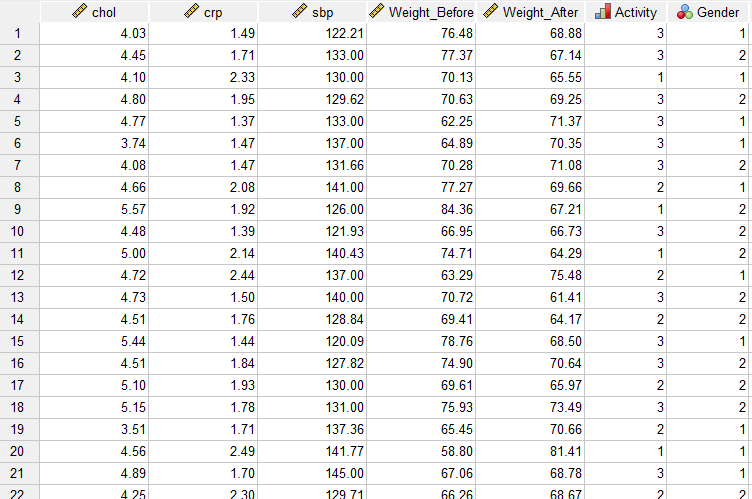
در تصویر زیر بخشی از فایل دیتا را مشاهده میکنید. در این فایل به بررسی چند شاخص قلبی و عروقی مانند crp ،chol و sbp بر روی وزن افراد میپردازیم. 150 نفر مرد و زن که میزان فعالیت بدنی و همچنین وزن قبل و بعد آنها پس از یک مداخله ورزشی به دست آمده، در این مثال گزارش شده است.
اندازه اثر در طرح یک نمونهای
Effect Size for One-Sample T Test
ایده محقق این است که میانگین وزن افراد قبل از مداخله ورزشی برابر با 68 کیلوگرم است. در واقع او میخواهد فرضیه زیر را آزمون کند.
$ \displaystyle {{H}_{0}}:{{\mu }_{{\left( {Before,Weight} \right)}}}=68kg\begin{array}{*{20}{c}} {} & {vs} & {} \end{array}{{H}_{1}}:{{\mu }_{{\left( {Before,Weight} \right)}}}\ne68kg$
ما میخواهیم علاوه بر آزمون فرضیه بالا، اندازه اثر اختلاف میانگین از عدد 68 کیلوگرم را نیز محاسبه کنیم. برای انجام این کار از مسیر زیر در نرمافزار SPSS استفاده میکنیم.
Analyze → Compare Means → One-Sample T Test
در این مرحله، پنجره زیر با نام One-Sample T Test برای ما باز میشود.
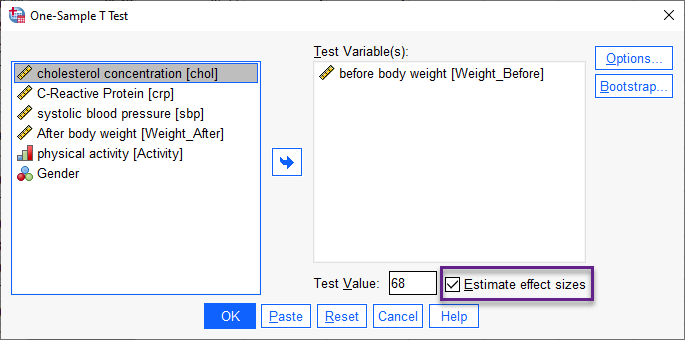
در کادر Test Variable(s) همان کمیت وزن قبل را قرار میدهیم. در بخش Test Value نیز عددی که میخواهیم با میانگین وزن افراد مقایسه شود، یعنی 68 نوشته میشود. نکته مهم این است که در این متن میخواهیم دربارهی اندازه اثر صحبت کنیم. بنابراین گزینه Estimate effect sizes را انتخاب میکنیم. با OK کردن در پنجره و محیط Output نرمافزار SPSS نتایج و جداول زیر به دست میآید. در ادامه دربارهی آنها توضیح میدهیم.
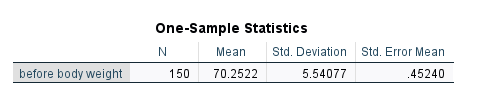
در ابتدای نتایج جدول One-Sample Statistics دیده میشود. در این جدول آمارههای توصیفی شامل تعداد نمونه، میانگین، انحراف معیار و انحراف معیار از میانگین برای وزن قبل افراد به دست آمده است. این جدول نشان میدهد میانگین و انحراف معیار وزن قبل به ترتیب برابر با 70.25 و 5.54 کیلوگرم است.
در خروجی نتایج جدول دیگری با نام One-Sample Test دیده میشود.

در این جدول نتایج آزمون فرضیه بالا یعنی بررسی میانگین وزن قبل افراد با عدد 68 کیلوگرم به دست آمده است. نتیجه به دست آمده بیانگر آن است که بین میانگین وزن افراد که برابر با 70.25 کیلوگرم به دست آمده است و عدد 68 کیلوگرم، اختلاف معنادار دیده میشود (P-value <0.001).
با این حال آنچه ما در این مقاله به دنبال آن بودیم، یافتن و به دست آوردن اندازه اثر است. در جدول زیر با نام One-Sample Effect Sizes این یافته به دست آمده است.

اندازه اثر بر مبنای روشهای Cohen’s d و Hedges’ correction به دست آمده است. عدد براورد شده برای اندازه اثر برابر با 0.406 و 0.404 است. Effect Size میتواند عددی مثبت و یا منفی باشد. من در عبارات زیر محدودههای مختلف عدد براورد شده برای قدرمطلق Effect Size را بیان کردهام.
-
- اندازه اثر 0.2 = d و کمتر را یک اندازه اثر کوچک و غیرمعنادار بیان میکنیم.
- اندازه اثر d بین 0.2 و 0.5 را اندازه اثر متوسط گزارش میکنیم.
- اندازه اثر d بین 0.5 و 0.8 اندازه اثر بزرگ و قوی بیان میشود
- اندازه اثر d > 0.8 نیز به عنوان یک اندازه اثر بسیار قوی گزارش میشود.
بنابراین در این مثال به دست میآید که اندازه اثر اختلاف بین میانگین وزن قبل افراد با عدد 68 کیلوگرم که برابر با 0.406 = d به دست آمده است، در رده متوسط قرار میگیرد. در جدول One-Sample Effect Sizes، فواصل اطمینان 95 درصد برای اندازه اثر نیز به دست آمده است. به عنوان مثال فاصله اطمینان 95 درصد برای d کوهن برابر با (0.572 ,0.239) گزارش میشود.
اندازه اثر در طرح دو نمونه وابستهEffect Size for Paired-Samples T Test
به عنوان یک مثال دیگر فرض کنید محقق میخواهد میانگین وزن قبل و بعد از مداخله ورزشی افراد را با یکدیگر مقایسه کند. او میخواهد فرضیه زیر را آزمون کند.
$ \displaystyle {{H}_{0}}:{{\mu }_{{\left( {Before,Weight} \right)}}}={{\mu }_{{\left( {After,Weight} \right)}}}\begin{array}{*{20}{c}} {} & {vs} & {} \end{array}{{H}_{1}}:{{\mu }_{{\left( {Before,Weight} \right)}}}\ne {{\mu }_{{\left( {After,Weight} \right)}}}$
ما میخواهیم علاوه بر آزمون فرضیه بالا، اندازه اثر اختلاف میانگین وزن قبل و بعد از مداخله را نیز محاسبه کنیم. برای انجام این کار از مسیر زیر در نرمافزار SPSS استفاده میکنیم.
Analyze → Compare Means → Paired-Samples T Test
مسیر انجام تحلیل Paired-Samples T Test در نرمافزار SPSS در این مسیر، پنجره زیر با نام Paired-Samples T Test برای ما باز میشود.
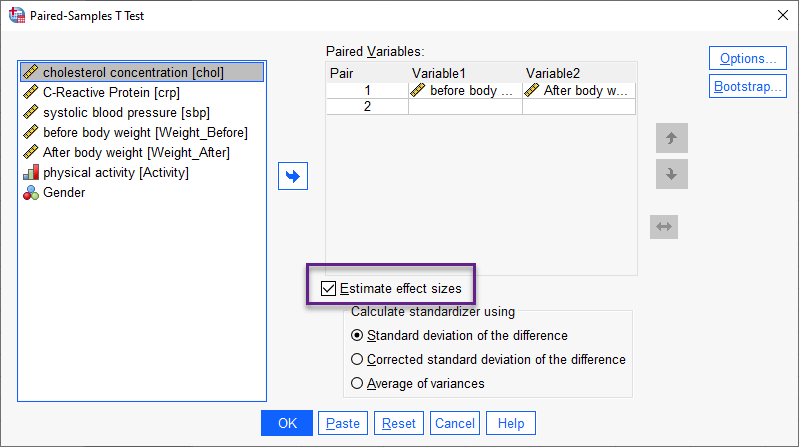
پنجره Paired-Samples T Test در کادر Paired Variables کمیتهای وزن قبل و بعد از مداخله را قرار میدهیم. از آنجا که میخواهیم اندازه اثر را نیز محاسبه کنیم، گزینه Estimate effect sizes را انتخاب میکنیم. با OK کردن در پنجره و محیط Output نرمافزار SPSS نتایج و جداول زیر به دست میآید. دربارهی آنها توضیح میدهیم.

جدول Paired Samples Statistics در ابتدای نتایج جدول Paired-Samples Statistics دیده میشود. در این جدول آمارههای توصیفی شامل تعداد نمونه، میانگین، انحراف معیار و انحراف معیار از میانگین برای وزن قبل و بعد از مداخله افراد به دست آمده است. این جدول نشان میدهد میانگین وزن قبل و بعد به ترتیب برابر با 70.25 و 68.63 کیلوگرم شده است.
در خروجی نتایج جدول دیگری با نام Paired Samples Test دیده میشود.

جدول Paired Samples Test در این جدول نتایج آزمون فرضیه بالا یعنی مقایسه میانگین وزن قبل و بعد افراد به دست آمده است. نتیجه به دست آمده نشان می دهد میانگین وزن قبل و بعد از مداخله با یکدیگر اختلاف معنادار دارند (P-value = 0.004).
اندازه اثر اختلاف قبل و بعد نیز که ما در این متن به دنبال آن بودیم در جدول زیر با نام Paired Samples Effect Sizes این یافته به دست آمده است.
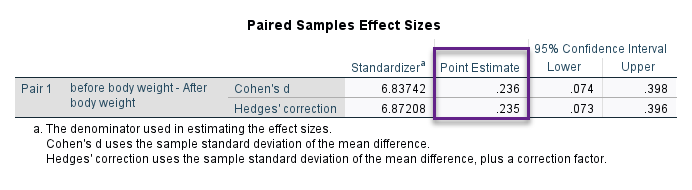
جدول Paired Samples Effect Sizes اندازه اثر بر مبنای روشهای Cohen’s d و Hedges’ correction به دست آمده است. عدد براورد شده برای اندازه اثر اختلاف بین میانگین وزن قبل و بعد از مداخله افراد برابر با 0.236 و 0.235 است. این Effect Size بیانگر وجود اندازه اثر تقریباً ضعیف و تاحدی متوسط اختلاف بین وزن قبل و بعد است.
اندازه اثر در طرح دو نمونه مستقلEffect Size for Independent-Samples T Test
فرض کنید محقق میخواهد اندازه کلسترول chol مردان و زنان را در این مثال با یکدیگر مقایسه کند. یعنی میخواهد فرضیه زیر را آزمون کند.
$ \displaystyle {{H}_{0}}:{{\mu }_{{\left( {Chol,women} \right)}}}={{\mu }_{{\left( {Chol,men} \right)}}}\begin{array}{*{20}{c}} {} & {vs} & {} \end{array}{{H}_{1}}:{{\mu }_{{\left( {Chol,women} \right)}}}\ne {{\mu }_{{\left( {Chol,men} \right)}}}$
ما میخواهیم علاوه بر آزمون فرضیه بالا، اندازه اثر اختلاف میانگین کلسترول مردان و زنان را نیز محاسبه کنیم. برای انجام این کار از مسیر زیر در نرمافزار SPSS استفاده میکنیم.
Analyze → Compare Means → Independent-Samples T Test
مسیر انجام تحلیل Independent-Samples T Test در نرمافزار SPSS در این مسیر، پنجره زیر با نام Independent-Samples T Test برای ما باز میشود.
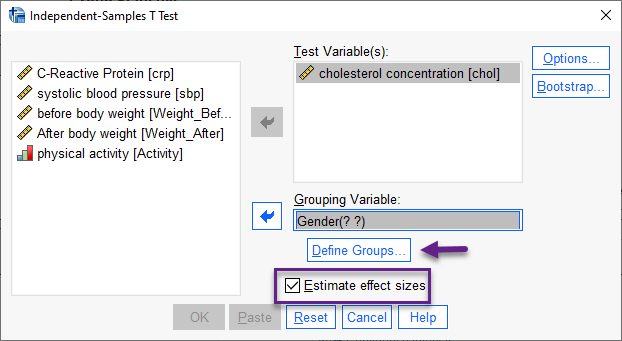
پنجره Independent-Samples T Test در کادر Test Variable(s) کمیت کلسترول را قرار میدهیم. از آنجا که میخواهیم اندازه اثر را نیز محاسبه کنیم، گزینه Estimate effect sizes را انتخاب میکنیم. در کادر Grouping Variable نیز کمیت جنسیت Gender را قرار میدهیم. در اینجا لازم است کدهای مربوط به زنان و مردان را برای آن تعریف کنیم. بنابراین بر روی کادر Define Groups کلیک میکنیم. وارد پنجره زیر میشویم.

پنجره Define Groups از آنجا که زنان و مردان را در فایل دیتا با کدهای 1 و 2 معرفی کردهایم، بنابراین همان کدها را در این پنجره وارد میکنیم. پس از آن Continue کرده و سپس OK میکنیم. با انجام این کار در پنجره و محیط Output نرمافزار SPSS نتایج و جداول زیر به دست میآید. دربارهی آنها توضیح میدهیم.

پنجره Group Statistics در ابتدای نتایج جدول Group Statistics دیده میشود. در این جدول آمارههای توصیفی شامل تعداد نمونه، میانگین، انحراف معیار و انحراف معیار از میانگین برای کلسترول مردان و زنان به دست آمده است. این جدول نشان میدهد میانگین کلسترول مردان و زنان به ترتیب برابر با 5.11 و 5.25 واحد است.
در خروجی نتایج، جدول دیگری با نام Independent Samples Test دیده میشود.

جدول Independent Samples Test در این جدول، نتایج آزمون فرضیه بالا یعنی مقایسه میانگین کلسترول مردان و زنان به دست آمده است. نتیجه به دست آمده نشان میدهد میانگین کلسترول مردان و زنان با یکدیگر اختلاف معنادار ندارند (P-value = 0.125).
اندازه اثر اختلاف میانگین کلسترول مردان و زنان، که به دنبال آن بودیم در جدول زیر با نام Independent Samples Effect Sizes به دست آمده است.
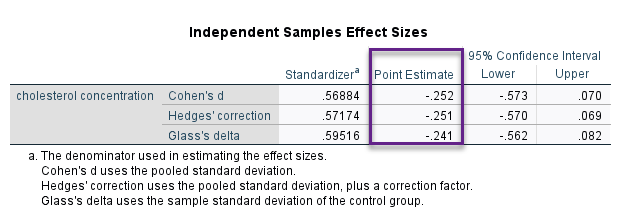
جدول Independent Samples Effect Sizes اندازه اثر بر مبنای روشهای Cohen’s d و Hedges’ correction و Glass’s delta به دست آمده است. عدد براورد شده برای اندازه اثر اختلاف بین میانگین کلسترول مردان و زنان برابر با 0.252- ، 0.251- و 0.241- است. این Effect Size بیانگر وجود اندازه اثر تقریباً متوسط اختلاف میانگین کلسترول در مردان و زنان است.
اندازه اثر در طرح آنالیز واریانسEffect Size for ANOVA
فرض کنید محقق میخواهد اندازه crp افراد در سطوح مختلف فعالیت بدنی را با یکدیگر مقایسه کند. او میخواهد بداند آیا crp در افراد با فعالیت بدنی مختلف، متفاوت است یا خیر. یعنی میخواهد فرضیه زیر را آزمون کند.
$ \displaystyle {{H}_{0}}:{{\mu }_{{\left( {crp,Low} \right)}}}={{\mu }_{{\left( {crp,Moderate} \right)}}}={{\mu }_{{\left( {crp,High} \right)}}}\begin{array}{*{20}{c}} {} & {vs} & {} \end{array}{{H}_{1}}:{{\mu }_{{\left( {crp,i} \right)}}}\ne {{\mu }_{{\left( {crp,j} \right)}}}$
ما میخواهیم علاوه بر آزمون فرضیه بالا، اندازه اثر اختلاف میانگین crp افراد در سطوح مختلف فعالیت بدنی آنها را نیز محاسبه کنیم. برای انجام این کار از مسیر زیر در نرمافزار SPSS استفاده میکنیم.
Analyze → Compare Means → One-Way ANOVA
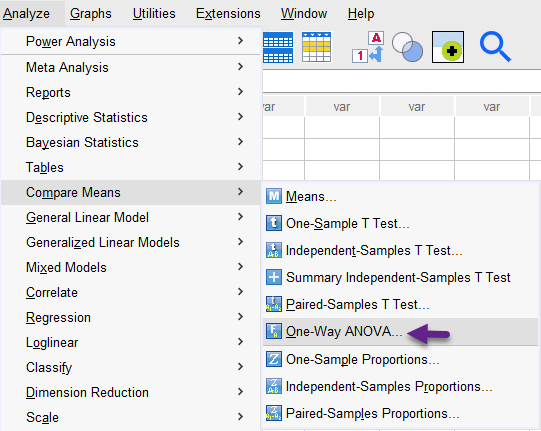
مسیر انجام تحلیل One-Way ANOVA در نرمافزار SPSS در این مسیر، پنجره زیر با نام One-Way ANOVA برای ما باز میشود.
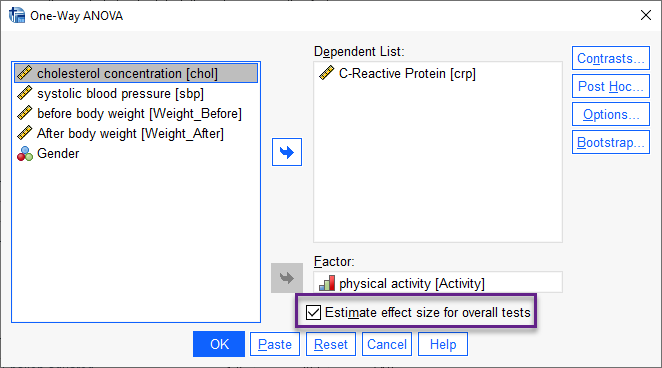
پنجره One-Way ANOVA در کادر Dependent List کمیت crp را قرار میدهیم. از آنجا که میخواهیم اندازه اثر را نیز محاسبه کنیم، گزینه Estimate effect sizes را انتخاب میکنیم. در کادر Factor نیز کمیت فعالیت بدنی Activity را قرار میدهیم.
از آنجا که در این مقاله به دنبال به دست آوردن اندازه اثر در طرحهای مختلف آزمون مقایسه میانگین هستیم، بنابراین با سایر گزینه و تنظیمات نرمافزار در این مرحله کاری نداریم. OK میکنیم. با انجام این کار در پنجره و محیط Output نرمافزار SPSS نتایج و جداول زیر به دست میآید. در ادامه دربارهی آنها توضیح میدهیم.
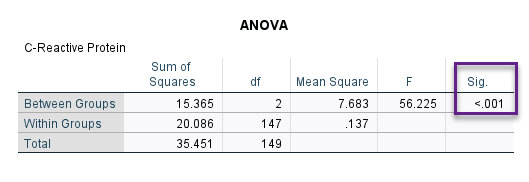
جدول ANOVA در ابتدای نتایج جدول ANOVA و یا همان آنالیز واریانس دیده میشود. در این جدول، نتایج آزمون فرضیه بالا یعنی مقایسه میانگین crp در گروههای مختلف فعالیت بدنی به دست آمده است. نتیجه به دست آمده نشان میدهد میانگین crp در سطوح مختلف فعایت بدنی با یکدیگر اختلاف معنادار دارند (P-value < 0.001).
اندازه اثر اختلاف میانگین crp در سطوح مختلف فعایت بدنی، که به دنبال آن بودیم در جدول زیر با نام ANOVA Effect Sizes به دست آمده است.
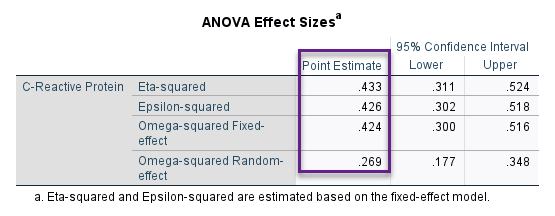
جدول ANOVA Effect Sizes اندازه اثر بر مبنای روشهای Omega-squared Fixed-effect ،Epsilon-squared ،Eta-squared و Omega-squared Random-effect به دست آمده است.
ما معمولاً Eta-squared را بیشتر مورد توجه قرار میدهیم. این همان اندازه اثری است که در تحلیلهای LM و GLM توسط نرمافزار محاسبه میشود. Effect Size براورد شده بر مبنای این روشها و از جمله Eta-squared که برابر با 0.433 به دست آمده است، بیانگر وجود اندازه اثر متوسط در بین اختلاف میانگین crp افراد با سطوح مختلف فهعایت بدنی است.
در این مقاله به موضوع اندازه اثر Effect Size در طرحهای مقایسه میانگین مانند One-Sample T Test ،Independent-Samples ،Paired Samples و One-Way ANOVA پرداختیم. یافتن اندازه اثر بر مبنای روشهای Cohen’s d و Hedges’ correction گزارش میشود. همچنین به بیان محدودههای مختلف عدد براورد شده برای قدرمطلق Effect Size اشاره کردیم. این مقاله با استفاده از نرمافزار SPSS به محاسبه اندازه اثر میپردازد.چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2022). Effect Size in mean comparison analyzes using SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/effect-sizes-compare-means-spss.php
For example, if you viewed this guide on 12th January 2022, you would use the following reference
GraphPad Statistics (2022). Effect Size in mean comparison analyzes using SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/effect-sizes-compare-means-spss.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.
