رگرسیون خطرات متناسب کاکس Cox Proportional Hazards Regression
Cox Proportional Hazards Regression
در این مقاله (مفاهیم اساسی در آنالیز بقا Survival Analysis) بیان کردیم که در تحلیل بقا، یکی از اهداف اولیه براورد و به دست آوردن رابطه بین کمیت پاسخ (مدت زمان سپری شده) و یک یا چند کمیت پیشبینی کننده است. این کمیتهای پیشبینیکننده ممکن است Variable هایی باشند که با شرایط آزمایشی مشخص شدهاند (مانند دریافت یک درمان در مقابل یک درمان متفاوت دیگر، یا یک کنترل)، یا ممکن است کمیتهای مشاهدهای (مانند جنسیت شرکتکننده در مطالعه) باشند.
همچنین در این مقاله (تحلیل کاپلان مایر Kaplan-Meier آنالیز بقا با نرمافزار Prism) گفتیم که کاپلان مایر و آزمونهای Log-Rank زمانی مفید هستند که کمیت پیشبینیکننده گروهبندی شده باشد (مثلاً درمان A در مقابل درمان B یا مردان در مقابل زنان). آنها جهت مقایسه احتمال بقا در بین این گروهها استفاده میشوند و برای پیشبینی کنندههای کمی مانند بیان ژن، وزن یا سن کار نمیکنند. در واقع کاپلان مایر، Univariate Analysis است و بقا را بر اساس یک عامل مورد بررسی توصیف میکند و تاثیر عوامل دیگر را نادیده میگیرد.
سوال چه نیازی به استفاده از مدل رگرسیون کاکس در تحلیلهای بقا وجود دارد؟
به منظور پاسخ به این سوال، ابتدا بیان میکنیم که آنالیز رگرسیون کاکس، یک Multivariate Analysis است که به منظور بررسی همزمان اثر چندین عامل خطر بر زمان بقا، استفاده میشود.
برای مثال، فرض کنید دو گروه از بیماران با هم مقایسه می شوند. آنهایی که ژنوتیپ خاصی دارند و آنهایی که ژنوتیپ خاصی ندارند. اگر یکی از گروه ها شامل افراد مسنتر نیز باشد، هر گونه تفاوت در بقا ممکن است به ژنوتیپ یا سن یا در واقع هر دو فاکتور نسبت داده شود. بنابراین در اینگونه موارد استفاده از آزمون کاپلان مایر چندان صحیح نیست و مطلوب است هنگام بررسی بقا در رابطه با یک عامل، تاثیر عامل دیگر (در این مثال سن افراد) اصطلاحاً تنظیم Adjust شود.
مدل آماری رگرسیون کاکس، یک ابزار پرکاربرد است که امکان آنالیز بقا را با توجه به چندین عامل به طور همزمان فراهم میکند. همچنین اندازه اثر را برای هر عامل ارائه میدهد.
هدف این مدل ارزیابی همزمان تاثیر چندین عامل بر بقا میباشد و این امکان را به ما میدهد تا بررسی کنیم که چگونه عوامل مشخص شده بر نرخ Rate وقوع یک رویداد (مثلاً عفونت، مرگ) در یک مقطع زمانی خاص تأثیر میگذارد. این نرخ معمولاً به عنوان نرخ خطر Hazard Rate شناخته میشود. کمیتهای پیشبینی کننده در ادبیات آنالیز بقا، کمیتهای کمکی Covariate نامیده میشوند.
- توضیحات بیشتر. علاقمند بودید متن زیر را هم بخوانید.
رگرسیون مخاطرات متناسب کاکس Cox Proportional Hazards Regression به منظور براورد اثر پیشبینی کنندههای مختلف بر زمان سپری شده تا رسیدن به رویداد مورد علاقه استفاده میشود. همانگونه که میدانیم اغلب (به ویژه در علوم زیستی)، رویداد مورد علاقه مرگ است و آنالیز بقا Survival Analysis نام دارد.
هدف از رگرسیون مخاطرات متناسب کاکس، طراحی مدلی برای نرخ خطر Hazard Rate مشاهده شده است که به طور مستقیم با تابع بقا Survival Function مرتبط است. سپس میتوان از این مدل برای ساختن منحنیهای بقا گروهها یا افراد خاص (بر اساس مقادیر Variable های پیشبینیکننده در مدل) استفاده کرد.
این همان کاری است که رگرسیونها برای ما انجام میدهند. یعنی ابتدا به طراحی مدل رگرسیونی بر مبنای دادههای موجود میپردازیم و در مرحلهی بعد به پیشبینی کمیت وابسته با استفاده از مقادیر عددی کمیتهای مستقل اقدام میکنیم.
معادله رگرسیون کاکس
Hazard Function
نکتهای که وجود دارد این است که در رگرسیون کاکس، کمیت وابسته Dependent Variable ما نرخ خطر است. در واقع مدل کاکس با تابع خطر نشان داده شده h(t) بیان میشود. تابع خطر را میتوان به عنوان خطر مرگ در زمان t تفسیر کرد و به صورت زیر تعریف میشود.
$\displaystyle h\left( t \right)={{h}_{0}}\left( t \right)\times \exp \left\{ {{{b}_{1}}{{x}_{1}}+{{b}_{2}}{{x}_{2}}+….+{{b}_{p}}{{x}_{p}}} \right\}$
که در آن
- $\displaystyle t$. زمان بقا را نشان میدهد.
- $\displaystyle h\left( t \right)$. تابع خطر را که توسط p کمیت Covariate یعنی $\displaystyle \left( {{{x}_{1}},{{x}_{2}},….,{{x}_{p}}} \right)$ توضیح داده میشود، بیان میکند. $\displaystyle t$ در $ \displaystyle h\left( t \right)$ به ما یادآوری میکند که خطر ممکن است در طول زمان تغییر کند.
- ضرایب $ \displaystyle \left( {{{b}_{1}},{{b}_{2}},….,{{b}_{p}}} \right)$ اثر Variableهای کمکی بر زمان بقا را نشان میدهند.
- $ \displaystyle {{h}_{0}}$. اصطلاحاً خطر پایه Baseline Hazard نامیده میشود. اگر تمام Xها برابر با صفر باشند، آنگاه $\displaystyle {{h}_{0}}\left( t \right)$ برابر با $\displaystyle h\left( t \right)$ خواهد بود.
اگر از طرفین رابطه بالا لگاریتم بگیریم در این صورت خواهیم داشت
$\displaystyle \log h\left( t \right)=\log {{h}_{0}}\left( t \right)+\left( {{{b}_{1}}{{x}_{1}}+{{b}_{2}}{{x}_{2}}+….+{{b}_{p}}{{x}_{p}}} \right)$
به این ترتیب مدل کاکس را میتوان به صورت یک رگرسیون خطی چندگانه از لگاریتم خطر روی کمیتهای $ \displaystyle {{{x}_{i}}}$ نوشت که در آن $\displaystyle \log {{h}_{0}}\left( t \right)$ به عنوان یک ضریب ثابت در مدل حضور دارد.
مقادیر $\displaystyle \exp \left\{ {{{b}_{i}}} \right\}$ نسبت خطر Hazard Ratio (HR) نامیده میشوند. مقدار $ \displaystyle {{{b}_{i}}}$ بزرگتر از صفر (یا معادل آن نسبت خطر بزرگتر از یک)، نشان میدهد که با افزایش مقدار کمیت کمکی iام، خطر اتفاق افتادن رویداد افزایش مییابد و در نتیجه طول بقا کاهش پیدا میکند.
به طور خلاصه میتوان نتایج زیر را برای نسبت خطر HR بیان کرد.
-
- HR = 1. نشاندهندهی عدم تاثیر بر نرخ خطر است.
- HR < 1. نرخ خطر را کاهش و در نتیجه طول بقا را افزایش میدهد.
- HR > 1. نرخ خطر را افزایش و در نتیجه طول بقا را کاهش میدهد.
-
- Ahmad T, Munir A, Bhatti SH, Aftab M, Raza MA (2017) Survival analysis of heart failure patients: A case study. PLoS ONE 12(7): e0181001. https://doi.org/10.1371/journal.pone.0181001
- Hypothesis tests (P values)
- Partial likelihood ratio test
- Wald test
- Score test
- Concordance statistics
به عنوان مثال توجه داشته باشید که در مطالعات سرطان، کمیت کمکی با نسبت خطر HR > 1 (یعنی b > 0) عامل پیش آگهی بد Bad Prognostic نامیده میشود. کمیت کمکی با نسبت خطر HR < 1 (یعنی b < 0) عامل پیش آگهی خوب Good Prognostic نامیده میشود.یک فرض کلیدی مدل کاکس این است که منحنیهای خطر برای گروههای مشاهدات (یا بیماران) باید متناسب Proportional باشند و همدیگر را قطع نکنند. اصولاً به همین دلیل است که نام درست مدل رگرسیون کاکس، رگرسیون خطرات متناسب کاکس Cox Proportional Hazards Regression است.دو بیمار k و ‘k را در نظر بگیرید که در مقادیر x متفاوت هستند. تابع خطر مربوطه را میتوان به سادگی به صورت زیر نوشت.
تابع خطر $\displaystyle {{h}_{k}}\left( t \right)$ برای بیمار k برابر است با
$\displaystyle {{h}_{k}}\left( t \right)={{h}_{0}}\left( t \right){{e}^{{\sum\limits_{{i=1}}^{p}{{\beta x}}}}}$
به همین ترتیب تابع خطر $\displaystyle {{h}_{{k’}}}\left( t \right)$ برای بیمار ‘k برابر است با
$\displaystyle {{h}_{{k’}}}\left( t \right)={{h}_{0}}\left( t \right){{e}^{{\sum\limits_{{i=1}}^{p}{{\beta x’}}}}}$
به این ترتیب نسبت خطر Hazard Ratio برای بیمار k و ‘k به صورت زیر خواهد بود
$\displaystyle \frac{{{{h}_{k}}\left( t \right)}}{{{{h}_{{k’}}}\left( t \right)}}=\frac{{{{h}_{0}}\left( t \right){{e}^{{\sum\limits_{{i=1}}^{p}{{\beta x}}}}}}}{{{{h}_{0}}\left( t \right){{e}^{{\sum\limits_{{i=1}}^{p}{{\beta x’}}}}}}}=\frac{{{{e}^{{\sum\limits_{{i=1}}^{p}{{\beta x}}}}}}}{{{{e}^{{\sum\limits_{{i=1}}^{p}{{\beta x’}}}}}}}$
نکته مهم در این رابطه این است که نسبت خطر، از زمان t مستقل است. در نتیجه، مدل کاکس یک مدل خطرات متناسب است. یعنی خطر رویداد در هر گروه، مضرب ثابتی (این مضرب ثابت همان عبارت $\displaystyle \frac{{{{e}^{{\sum\limits_{{i=1}}^{p}{{\beta x}}}}}}}{{{{e}^{{\sum\limits_{{i=1}}^{p}{{\beta x’}}}}}}}$ است که به t ربطی ندارد و از آن مستقل است) از خطر در هر گروه دیگری است. این فرض حاکی از آن است که همانطور که در بالا ذکر شد، منحنیهای خطر برای گروهها باید متناسب باشند و نمیتوانند همدیگر را قطع کنند.
به عنوان مثال اگر فردی در یک نقطه زمانی اولیه دو برابر فرد دیگر، خطر مرگ داشته باشد، در تمام زمانهای بعدی نیز خطر مرگ دو برابر بیشتر خواهد بود.
علاقمند بودید در لینک (نسبت خطر Hazard Ratio در آنالیز بقا چیست؟) دربارهی نسبت خطر بیشتر مطالعه کنید.
مثال کار با نرمافزار PrismExample
مانند هر تحلیل دیگری که با نرمافزار Prism انجام میدهیم، گام اول برای آنالیز دادهها و شروع کار با این نرمافزار، ورود دادهها و یا استفاده از مثالهای آموزشی موجود است. خوشبختانه Prism یک مثال آموزشی در موضوع رگرسیون خطرات متناسب کاکس دارد. ما نیز از همین مثال نرمافزار استفاده میکنیم. این مثال را میتوانید در تحلیلهای Multiple variables مشاهده کنید. فایل دیتا این مثال را میتوانید از اینجا دریافت کنید.
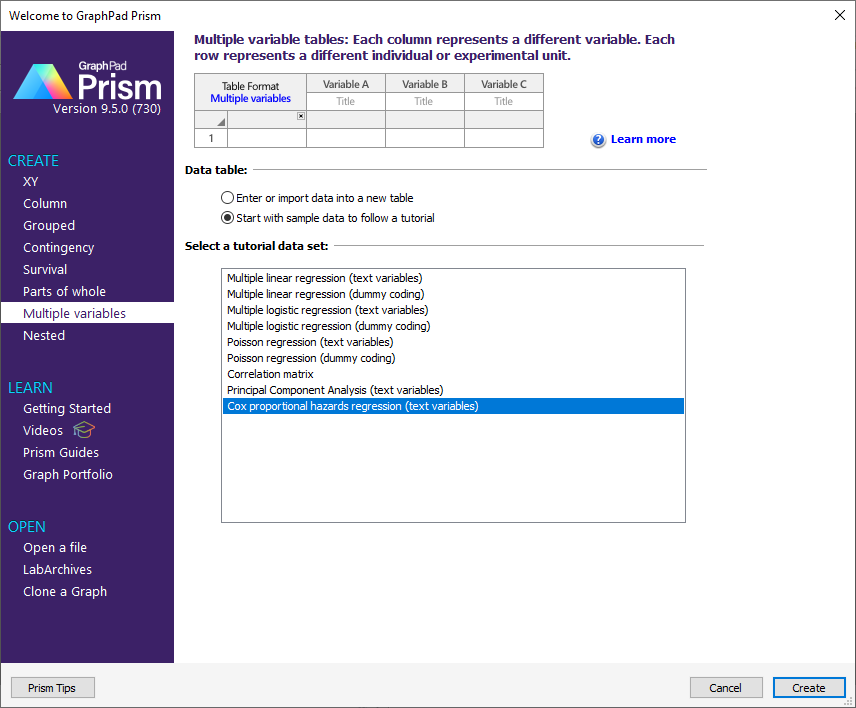
مثال Cox Proportional Hazards Regression در نرمافزار Prism با Create کردن این مثال، فایل دیتا زیر برای ما باز میشود. تصویر آن در ادامه آمده است.
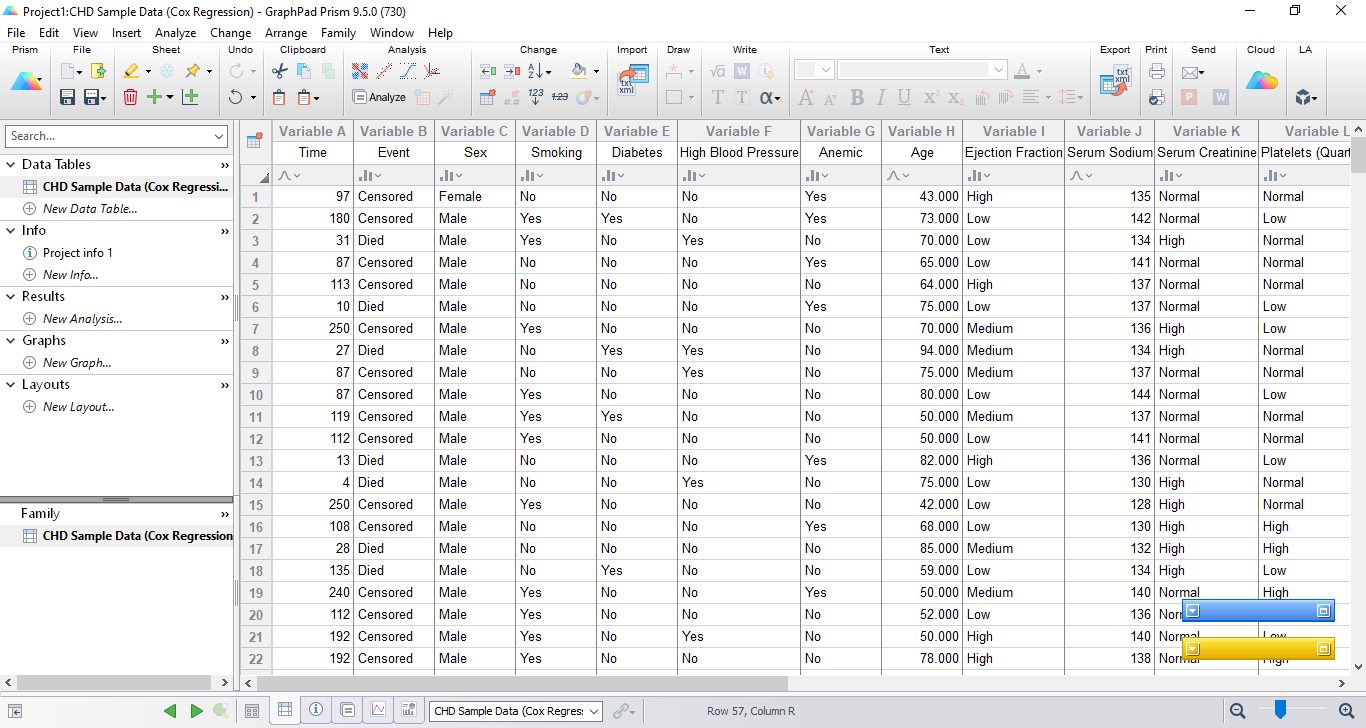
فایل دیتا مثال Cox Proportional Hazards Regression در نرمافزار Prism این دادهها از مقالهی اصلی زیر به دست آمدهاند.
این داده ها از 299 بیمار (105 زن و 194 مرد) که بین آوریل تا دسامبر 2015 در انستیتوی قلب و عروق بیمارستانی در پاکستان بستری شده بودند جمعآوری شد. برای هر بیمار، اطلاعات مربوط به کمیتهای زیر به دست آمد.
1. جنسیت 2. وضعیت سیگار کشیدن 3. وضعیت دیابت 4. فشار خون (طبقهبندی شده به عنوان نرمال یا بالا) 5. کمخونی (بررسی سطح هماتوکریت) 6. سن 7. کسر دفعی (طبقهبندی شده به عنوان کم، متوسط یا زیاد) 8. سطح سدیم سرم 9. سطح کراتینین سرم (طبقه بندی شده به عنوان نرمال یا زیاد) 10. تعداد پلاکتها (طبقهبندی شده به عنوان کم، نرمال یا زیاد) و 11. کراتینین فسفکیناز (CPK).
1Sex 2. Smoking status 3. Diabetes status 4. Blood pressure (classified as normal or high) 5. Anemia (assessed via hematocrit levels) 6. Age 7. Ejection fraction (classified as Low, Medium, or High) 8. Serum sodium levels 9. Serum Creatinine levels (classified as Normal or High) 10. Platelet counts (classified as Low, Normal or High) and 11. Creatinine phosphokinase (CPK)
علاوه بر آن، زمان بقای سپری شده (مدت زمان مشاهده شده) برای هر بیمار همراه با پیامد مشاهده شده (مرگ در نتیجه بیماری عروق کرونر قلب، CHD یا سانسور بیمار) ثبت شده است.
در این دادهها هر ردیف بیانگر یک فرد متفاوت در مطالعه است. ستونها هر کدام نشاندهنده یک Variable مورد بررسی در این افراد هستند که نام آنها را در بالا بیان کردیم. ستون با نام “Time” نشاندهنده زمان بقای سپری شده (یا زمان سانسور) برای هر بیمار است و ستون با نام “Event” نشان میدهد که آیا بیمار در نتیجه CHD فوت کرده است (رویداد = 1) یا سانسور شده است (رویداد = 0).
در این مطالعه به دنبال بررسی نحوه اثرگزاری کمیتهای مختلف (نامبرده شده در بالا) بر روی مدت زمان بقای بیماران مورد بررسی هستیم. به همین دلیل مناسب است که از مدل رگرسیون خطرات متناسب کاکس که به اختصار آن را رگرسیون کاکس مینامیم، استفاده کنیم.
تنظیمات نرمافزارSetting
جهت شروع تحلیل با نرمافزار Prism در همان فایل دادهها، دکمهی
 در نوار ابزار بالای صفحه را میزنیم. پس از آن در پنجره باز شده و از لیست Multiple variable analyses گزینهی Cox proportional hazards regression را انتخاب میکنیم. تصویر زیر را ببینید.
در نوار ابزار بالای صفحه را میزنیم. پس از آن در پنجره باز شده و از لیست Multiple variable analyses گزینهی Cox proportional hazards regression را انتخاب میکنیم. تصویر زیر را ببینید.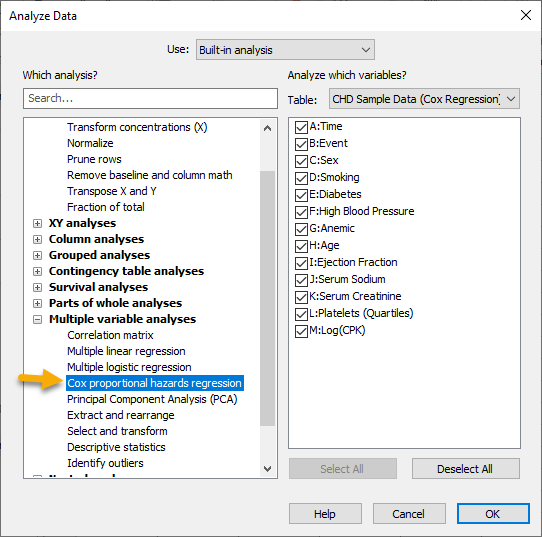
انتخاب گزینهی Cox proportional hazards regression با انجام این کار، پنجره Parameters Cox proportional hazards regression برای ما باز میشود. آن را در تصویر زیر ببینید.

پنجره Parameters Cox proportional hazards regression نرمافزار پریسم به ما توصیه میکند که همهی تنظیمات پیشفرض را بپذیریم و OK کنیم. با این حال از آنجا که ما به دنبال آموزش این مدل رگرسیونی و کار با Prism هستیم، سعی میکنم به بیان بخشها و کادرهای مختلف پنجره تنظیمات نرمافزار جهت اجرای رگرسیون کاکس، بپردازم. پنجره Parameters Cox proportional hazards regression شامل هشت تب است. در ادامه به توضیح هر یک میپردازم.
در این تب، کمیتهای زمان تا رسیدن به رویداد (پاسخ) و نتیجه (رویداد/سانسور) را مشخص کنید. این دو Variable برای هر تحلیل رگرسیون خطرات متناسب کاکس مورد نیاز است. مشخص کنید کدام مقدار (یا سطح) مشاهدات را با «رویدادها» نشان میدهد و کدام مقادیر نشاندهنده مشاهدات «سانسور شده» است.
گاهی اوقات این امکان وجود دارد که در فایل دادهها، علاوه بر مقادیر صفر و یک که بیانگر دادههای سانسور شده و رویداد است، اندازههای دیگری نیز وجود داشته باشد. در این تب تعیین کنید که چگونه هر مقدار یا سطح دیگری را مدیریت کنیم، معمولاً ما آنها را به عنوان Missing تعریف میکنیم.
همچنین در این برگه، نحوه برخورد Prism با گرهها Ties را در زمانهای سپری شده نشان دهید. دربارهی گرهها توضیح اینکه مدل رگرسیون خطرات متناسب کاکس مستلزم آن است که اطلاعات زمان تا رسیدن به رویداد برای هر مشاهده ثبت شود و ترتیب این زمانها برای محاسبه تحلیل مهم است. با این حال، اغلب موقعیتهایی وجود دارد که در آنها چندین رویداد ثبت میشوند و سبب میشود زمان سپری شده یکسانی داشته باشند (خواه به دلیل نحوه جمعآوری دادهها یا به دلیل ناشناخته بودن ترتیب خاص رویدادها). هنگامی که مشاهدات رویداد دارای زمانهای سپری شده یکسانی هستند، گفته میشود که این مشاهدات “گره خورده” هستند. روشهای مختلفی وجود دارد که میتوان گرهها را مدیریت کرد. به طور پیش فرض، Prism بهترین روش را برای مدیریت گرهها انتخاب میکند. بسته به تعداد گرهها، Prism یا از روش Exact یا روش Efron استفاده میکند.
در نهایت، با استفاده از بخش «تعریف مدل»، کمیتهای پیشبینیکننده، اثرات متقابل و یا احتمالاً تبدیلهایی را که میخواهید در مدل گنجانده شوند، انتخاب کنید. به صورت پیشفرض گزینه Main effects انتخاب شده است. این کار باعث میشود فقط اثرات اصلی هر کمیت مستقل در مدل رگرسیونی حضور داشته باشد. در اغلب موارد این انتخاب، بهترین انتخاب است. با این حال نرمافزار Prism به ما اجازه میدهد که اثرات متقابل دو و سه طرفه Two/Three-way Interaction را نیز در مدل رگرسیونی قرار دهیم.
علاوه بر همه اینها، نرمافزار این امکان را نیز به ما میدهد که مربع، مکعب، ریشه مربع، لگاریتم یا نمایی هر کمیت پیشبینی را در مدل قرار دهید. برای انجام این کار به سادگی گزینه Transform را انتخاب کنید، و سپس مشخص کنید که کدام کمیتهای پیشبینی را میخواهید تبدیل کنید.
هنگامی که پیشبینیکنندههای ما نه به صورت پیوسته Continuous بلکه به صورت طبقهای Categorical تعریف میشوند، نرمافزار از ما میخواهد که برای هر کدام از این کمیتهای طبقهای، یک سطح رفرنس تعیین شود. انجام این کار مهم است، به دلیل اینکه تحلیل نتایج در آن کمیت گروهبندی شده بر مبنای همین سطح رفرنس انجام میشود. در تصویر زیر، تب Reference level را ببینید.
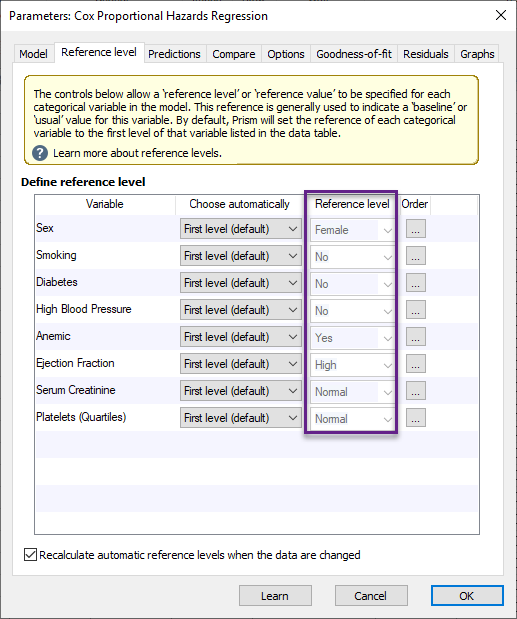
تب Reference level در مدل رگرسیون کاکس نرمافزار به صورت پیشفرض، سطح اول First level را به عنوان سطح رفرنس تعریف میکند. منظور از First Level نیز در اینجا متن قرار گرفته در اولین مشاهده به ازای هر کمیت است. چنانچه بخواهیم سطح رفرنس را ویرایش کنیم، این کار به سادگی با استفاده از ستون Choose automatically قابل انجام است.
به عنوان مثال مدلی را در نظر بگیرید که شامل کمیت پیشبینیکننده طبقهبندی «جنس» با سطوح «مرذ» و «زن» است. اگر مرذ سطح رفرنس ما باشد، مدل پیشبینیشده شامل یک ضریب بتا (و نسبت خطر) برای زن میشود و دیگر ضریب رگرسیونی برای مرد را شامل نمیشود. نسبت خطر برای زن در این مورد به ما میگوید (با فرض ثابت نگه داشتن سایر کمیتها) نرخ خطر برای زنان چند برابر بیشتر یا کمتر از مردان است. به عبارت دیگر، اگر نسبت خطر برای زن برابر با 3.658 باشد، انتظار میرود نرخ خطر برای زنان 3.658 برابر بیشتر از مردان باشد.
از این تب میتوانیم بر مبنای مدل براورد شده توسط پریسم، جهت پیشبینی احتمال بقا با استفاده از قرار دادن مقادیر دلخواه برای هر کدام از کمیتهای پیشبینی کننده، همراه با زمان سپری شده مشخص، استفاده کرد. این کاری است که برخی از نرمافزارهای آماری مانند Minitab هنگامی که مدل رگرسیونی برای ما براورد میکنند، انجام میدهند.
در تصویر زیر میتوانید تب Predictions را مشاهده کنید.
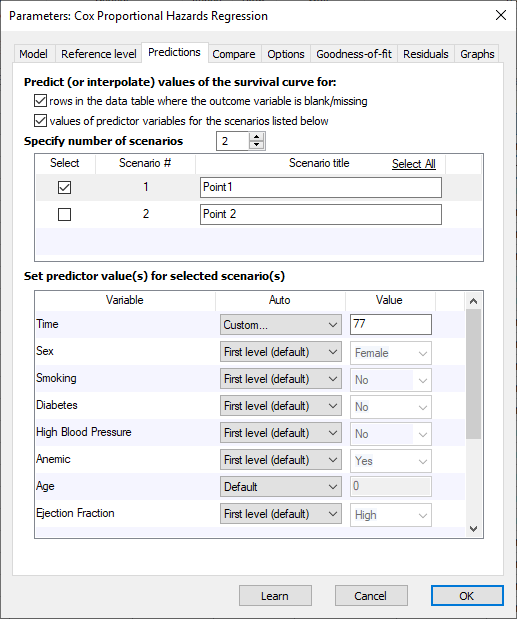
تب Predictions در رگرسیون کاکس جهت درک این تب از اینجا شروع میکنیم که هدف از رگرسیون خطرات متناسب کاکس براورد میزان خطر (و متعاقباً تابع بقا) برای جمعیت مشاهده شده است. مقدار تابع خطر نه تنها به زمان سپری شده تا رسیدن به رویداد مورد علاقه، بلکه به مقادیر هر یک از کمیتهای پیشبینی موجود در مدل نیز بستگی دارد. با استفاده از مدل برازش و مقادیر شناخته شده هر کمیت پیشبینیکننده در مدل، میتوان برای احتمال بقا، براوردی در مقاطع زمانی معین پیشبینی کرد. این مطلب یک ویژگی جالب توجه در نرمافزار Prism است و البته ارتباطی با انجام رگرسیون کاکس ندارد و میتوان آن را نادیده گرفت مگر اینکه پیشبینیهای خاصی از مدل مورد نظر ما باشد.
به عنوان مثال من در تب بالا، دو سناریو (با مقادیر متفاوت کمیتهای پیشبینی کننده) تعریف کردهام و از نرمافزار خواستهام بر مبنای اعداد داده شده، احتمال بقا را پیشبینی کند. البته همانگونه که در بالا نوشتهام این کار ضروری نیست و نرمافزار مدل رگرسیون کاکس را بدون قرار دادن تنظیمات خاصی در این تب نیز انجام میدهد.
با استفاده از این تب میتوانید به مقایسه مدل رگرسیون کاکس مثلاً با اثرات اصلی با یک ندل رگرسیون کاکس دیگر شامل اثرات متقابل، پرداخت. تصویر زیر را ببینید.
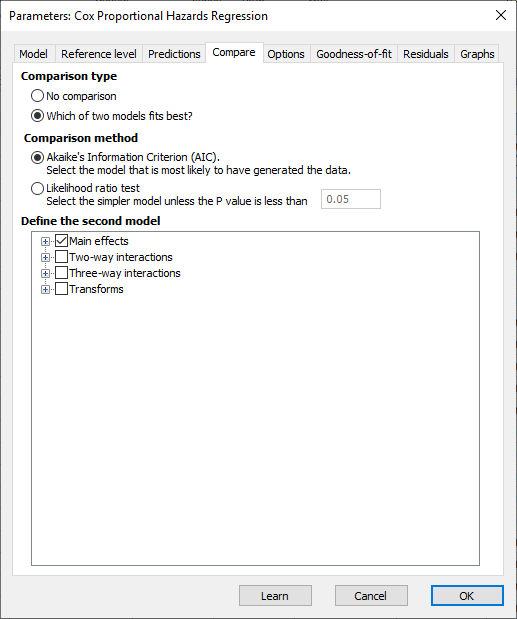
تب Compare در تنظیمات رگرسیون کاکس بر مبنای تب Options مشخص کنید که Prism کدام نتایج را باید گزارش کند. در تصویر زیر آن را ببینید.
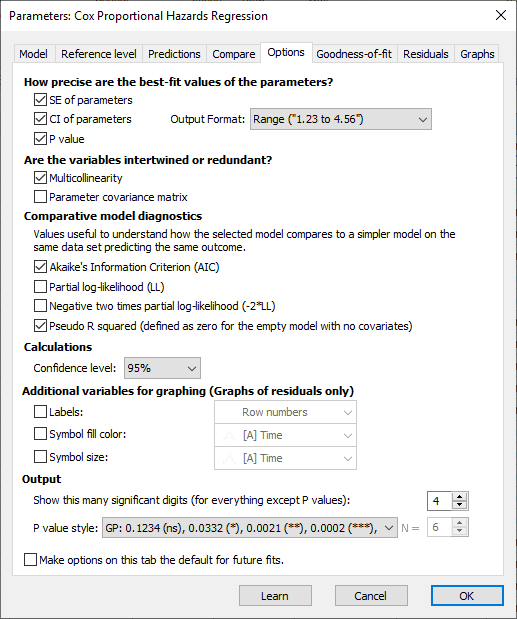
تب Options در رگرسیون کاکس تب Options برای رگرسیون خطرات متناسب کاکس تعدادی گزینه و نتایج اختیاری ارائه میدهد که Prism میتواند گزارش دهد. این گزینهها در سایر تحلیلهای قابل انجام با این نرمافزار مانند رگرسیون خطی چندگانه و رگرسیون لجستیک چندگانه نیز دیده میشوند. من در تب بالا برخی از آنها را انتخاب کردهام. توضیح بیشتر آنها را به هنگام به دست آوردن نتایج و خروجیهای نرمافزار میتوان مشاهده کرد.
در این تب که با نام نیکویی برازش بیان میشود، مشخص کنید که Prism کدام معیارهای تحلیل را باید گزارش کند. هر یک از اینها بینشی در مورد اینکه مدل چقدر با دادهها مطابقت دارد، ارایه میدهد. در تصویر زیر این تب را ببینید.
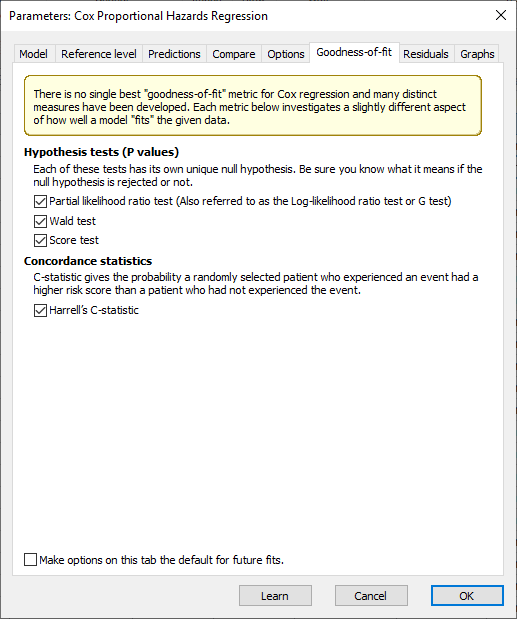
تب Goodness-of-fit در تنظیمات رگرسیون کاکس معیارهای نیکویی برازش مدل رگرسیون خطرات متناسب کاکس را میتوان در دو دسته اصلی قرار داد. من در ادامه دربارهی هر یک از آنها توضیح دادهام.
نرمافزار چندین تست مختلف که میتواند هنگام انجام رگرسیون خطرات متناسب کاکس گزارش شود، ارایه میکند. این تستها عبارتند ازریاضیات مورد استفاده برای انجام این آزمونها نسبتاً پیچیده است و وابسته به تابع احتمالی است که جهت تعیین بهترین مقادیر ضرایب پارامتر مدل (مقادیر β) استفاده میشود. با این حال، هر یک از این آزمونها از فرضیههای صفر مشابهی استفاده میکنند که فرض میکنند هیچ کدام از کمیتهای پیشبینیکننده اطلاعاتی برای کمک به براورد خطر (یا بقا) در مدل رگرسیون ارایه نمیدهند. به معنای اینکه هیچکدام از X تاثیر معناداری بر بقا ندارند. به عبارت دیگر، این آزمونها مدلهای رگرسیون زیر را با هم مقایسه میکنند.
$\displaystyle {{H}_{0}}:h\left( t \right)={{h}_{0}}\left( t \right)\begin{array}{*{20}{c}} {} & {vs} & {} \end{array}{{H}_{1}}:h\left( t \right)={{h}_{0}}\left( t \right)\times {{e}^{{\sum{{\left( {{{x}_{i}}{{\beta }_{i}}} \right)}}}}}$
آماره آزمون برای هر یک از سه تست بالا کمی متفاوت است، با این حال همه به طور مشابه ارزیابی میشوند. هر آزمون یک آماره کای دو و یک P value متناظر را تولید میکند. با فرض اینکه فرضیه صفر (همه مقادیر بتا صفر هستند) درست باشد، مقدار احتمال به دست آمده بزرگ خواهد بود. به همین ترتیب عدد P کوچک نشان میدهد که فرض صفر باید رد شود و حداقل یک X معنادار در مدل وجود دارد.
نرمافزار گزینهای را جهت گزارش آماره C هارل Harrell’s C برای تطابق ارایه می دهد. ما این گزینه را انتخاب میکنیم و توضیحات بیشتر را در بخش نتایج و خروجیهای نرمافزار بیان میکنیم. علاقمند بودید این لینک را نیز ببینید.
آماره C میتواند عددی بین صفر تا یک را به خود بگیرد. مقدار یک نشان میدهد که مدل به درستی زمان بقای طولانیتری (نسبت خطر کوچکتر) را برای هر جفت مشاهدات پیشبینی کرده است. آماره C نزدیک به 0.5 نشان میدهد که مدل به درستی تنها 50 درصد از جفتهای مشاهده را پیشبینی میکند، به این معنی که مدل بهتر از شانس تصادفی (مانند “پرتاب سکه”) عمل نمیکند. مقادیر کمتر از 0.5 نشان میدهد که مدل بدتر از شانس تصادفی عمل میکند و خب به معنای آن است که مدل مناسب نیست و به خوبی کار نمیکند. این نوشتهها ما را به یاد منحنی ROC میاندازد. علاقمند بودید در این مقاله (منحنی ROC ، نقطه برش ، حساسیت و ویژگی) آن را هم ببینید.
در این تب انتخاب کنید که نرمافزار کدام باقیماندهها را گزارش و نمودار آنها را رسم کند. توجه داشته باشید که “Residuals” رگرسیون خطرات متناسب کاکس از نظر ریاضی با باقیماندههای رگرسیون خطی متفاوت است. با این حال، آنها را میتوان جهت پاسخ به سوالات و آزمون فرضیات مشابه که در همهی مدلهای رگرسیونی استفاده میشود، به کار برد. در تصویر زیر میتوانید تب Residuals را مشاهده کنید.
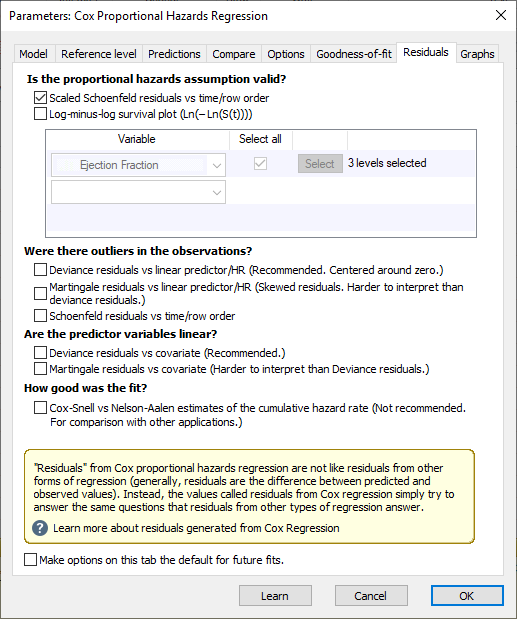
تب Residuals در تنظیمات رگرسیون خطرات متناسب کاکس به دلیل اهمیت گزینهها و نتایج به دست آمده از این تب که عمدتاً گراف و نمودار هستند، من در لینک (باقیمانده ها Residuals در رگرسیون خطرات متناسب کاکس) به صورت جداگانه به توضیح این تب پرداختهام. علاقمند بودید آن را ببینید.
Graphsتجسم نتایج تحلیل در قالب نمودار یکی از بهترین راهها برای درک یافتههایی نرمافزار است. در رگرسیون کاکس، بررسی احتمال بقای براورد شده در طول زمان، برای گروههای مختلف، جالب است. این گروهها با مقادیر کمیتهای پیشبینیکننده در مدل رگرسیون تعریف میشوند (برای مثال، زنان در برابر مردان یا سیگاریها در برابر غیر سیگاریها).
به دلیل اهمیت موضوعات مرتبط با این تب، من در یک مقاله جداگانه به بیان گزینههای مختلف و نحوه کار با تب Graphs پرداختهام. علاقمند بودید لینک (تنظیمات رسم نمودارها Graphs در رگرسیون خطرات متناسب کاکس) را ببینید.
نتایج رگرسیون خطرات متناسب کاکسResults & Graphs
من بیان نتایج، خروجیها و گرافهای به دست آمده از رگرسیون کاکس را در یک مقاله جداگانه نوشتهام. علاقمند بودید به لینک (نتایج و خروجی های تحلیل رگرسیون خطرات متناسب کاکس) مراجعه کنید.
ما در این مقاله به بررسی مدل رگرسیون خطرات متناسب کاکس Cox Proportional Hazards Regression که یکی از انواع تحلیلهای آنالیز بقا میباشند، با استفاده از نرمافزار Prism پرداختیم. در این مقاله به نحوه ورود دادهها به نرمافزار، بیان مثال، تنظیمات، تبها و گزینههای مختلف موجود در نرمافزار جهت اجرای رگرسیون کاکس، اشاره کردیم.چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2023). Cox proportional hazards regression. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/Cox-proportional-hazards-regression/.php
For example, if you viewed this guide on 12th January 2023, you would use the following reference
GraphPad Statistics (2023). Cox proportional hazards regression. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/Cox-proportional-hazards-regression/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.


