تحلیل سری زمانی Winters' Method با نرم‌افزار Minitab

Winters’ Method

از Winters’ Method برای جداسازی یک سری زمانی به اجزای روند Trend، فصلی Seasonal و سطح Level استفاده می‌کنیم. در واقع این روش به منظور هموار کردن داده‌ها و ارایه پیش‌بینی های میان مدت، هنگامی که داده‌ها دارای روند و اثر فصلی هستند، استفاده می‌شود. درباره‌ی مفهوم هموارسازی هم توضیح اینکه این کار جهت حذف نوسان و نویز در مجموعه داده‌ها انجام می‌شود. ایده هموارسازی این است که می‌تواند پراکندگی‌های ساده شده موجود در داده‌ها را شناسایی کند و به پیش‌بینی الگوهای مختلف کمک کند. در بازارهای مالی، نویز می‌تواند شامل اصلاحات کوچک قیمت در بازار و همچنین نوسانات قیمت باشد که روند کلی داده‌ها را مخدوش می‌کند.

هنگامی که با استفاده از نرم‌افزار Minitab به تحلیل Winters’ Method می‌پردازیم، می‌توانیم انتخاب کنیم که اثر فصلی Seasonal Component به صورت روند افزایشی یا ضربی باشد. از این تحلیل برای ایجاد پیش‌بینی و ارزیابی مولفه‌ها هنگامی که داده‌ها دارای یک اثر فصلی دارای روند هستند، استفاده می‌کنیم.

به عنوان مثال، یک برنامه‌ریز بودجه برای دفتر تجاری محلی از تحلیل روش Winters جهت پیش‌بینی هزینه‌های آب و برق سه دوره بعدی استفاده می‌کند.

جهت انجام تحلیل Winters، از مسیر زیر در نرم‌افزار Minitab استفاده می‌کنیم.

Stat → Time Series → Winters’ Method

تحلیل‌های جایگزین. اگر داده‌های شما فاقد روند هستند و جز فصلی Seasonal Component ندارند، از میانگین متحرک Moving Average یا هموارسازی نمایی منفرد Single Exponential Smoothing استفاده کنید.

اگر داده‌های شما روند دارند اما فاقد مولفه فصلی هستند، از Trend Analysis یا Double Exponential Smoothing استفاده کنید.

مثال آنالیز Winters’ Method

Example

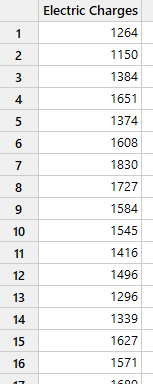
برنامه‌ریزان بودجه یک دفتر تجاری می‌خواهند هزینه‌های برق سال آینده را پیش‌بینی کنند. آنها داده‌هایی را در مورد استفاده از خدمات شهری در 84 دوره صورتحساب قبلی را جمع‌آوری کرده‌اند تا بتوانند ماه‌های آینده را پیش بینی کنند. فایل دیتا این مثال را می‌توانید از اینجا Winters’ Method دریافت کنید. در تصویر زیر بخشی از داده‌ها را مشاهده می‌کنید.

خوب است در ابتدا یک نمودار سری زمانی از داده‌های مثال رسم کنیم. این کار به ما کمک می‌کند تا درکی از داده‌های مورد مطالعه داشته باشیم. علاقمند بودید می‌توانید در لینک (رسم نمودارهای سری زمانی Time Series Plot) با انواع گراف‌های سری زمانی در نرم‌افزار Minitab آشنا شوید.

در تصویر زیر، من گراف سری زمانی داده‌های هزینه‌های برق برای 84 ماه قبل را آورده‌ام.

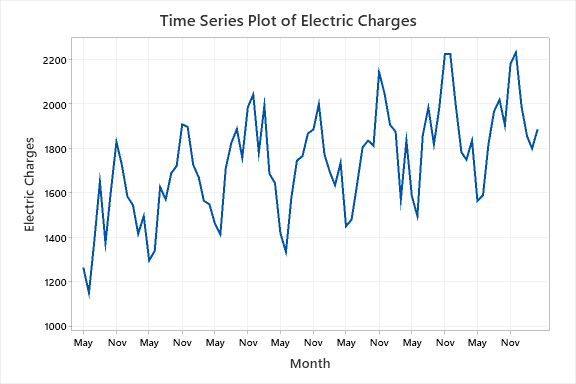
همان‌گونه که در گراف سری زمانی هزینه‌های برق دیده می‌شود، یک روند فصلی در داده‌ها وجود دارد، به گونه‌ای که در هر سال کمترین فروش مربوط به ماه May است. پس از آن داده‌ها تا ماه Nov روند افزایشی خواهند داشت و بار دیگر تا May سال بعد دارای روند کاهشی در میزان هزینه‌های برق هستند.

وجود روند فصلی در داده‌ها سبب شده است که از تحلیل سری زمانی Winters’ Method استفاده کنیم.

از مسیر زیر آنالیز Winters’ Method در نرم‌افزار Minitab انجام می‌شود.

مسیر آنالیز Winters’ Method در نرم‌افزار Minitab

در این صورت پنجره زیر با نام Winters’ Method برای ما باز می‌شود.

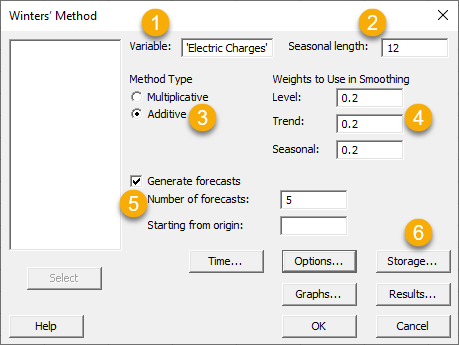
من پنجره بالا را شماره‌گزاری کرده‌ام و در ادامه به ترتیب شماره‌ها به توضیح هر بخش می‌پردازم.

1 ستون با نام Electric Charges که بیانگر میزان هزینه مصرف برق در هر ماه است، در کادر Variable قرار می‌گیرد.

2 از آن‌جا که با یک روند فصلی 12 ماهه روبه‌رو هستیم و دوره تناوب هزینه برق به صورت سالانه است، در بخش Seasonal length عدد 12 را می‌نویسیم.

در Seasonal length، تعداد مشاهداتی را که در یک فصل رخ می‌دهد وارد کنید. به عنوان مثال، اگر داده‌ها را به صورت ماهانه جمع‌آوری می‌کنید و الگوی سالانه دارند، عدد 12 را وارد کنید. اگر طول الگوی فصلی را نمی‌دانید، از مسیر Stat > Time Series > Autocorrelation در نرم‌افزار Minitab برای کمک به شناسایی طول استفاده کنید.

3 در کادر Model Type گزینه Additive را انتخاب می‌کنیم. در اینجا گزینه دیگری نیز با نام Multiplicative دیده می‌شود. به نظرم بهتر است درباره‌ی این گزینه‌ها بیشتر توضیح دهیم.

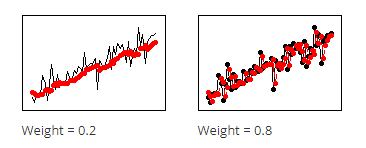
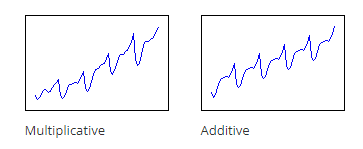در ابتدا گراف‌های مقابل را ببینید. آن‌ها چه تفاوتی با هم دارند؟

پاسخ این است مدل Multiplicative هنگامی انتخاب می‌شود که بزرگی الگوی فصلی با طی شدن زمان در داده‌ها افزایش (و یا کاهش) می‌یابد. جهت فهم بهتر به گراف Multiplicative نگاه کنید. کف و سقف داده‌ها در هر روند فصلی در یک محدوده بالاتر قرار گرفته است.

به همین ترتیب مدل Additive هنگامی انتخاب می‌شود که مقدار الگوی فصلی با طی شدن زمان در داده‌ها ثابت می‌ماند.

نکته

اگر نمی‌دانید در داده‌های خود از مدل Multiplicative و یا Additive استفاده کنید، می‌توانید ابتدا گراف سری زمانی داده‌ها را رسم کنید. برای انجام این کار لینک (رسم نمودارهای سری زمانی Time Series Plot) را ببینید. این کار به شما یک دید کلی درباره‌ی داده‌ها ارایه می‌کند.

راهکار دیگر این است که هم مدل Multiplicative و هم مدل Additive را بر داده‌های خود برازش دهید. سپس ببینید کدام مدل اندازه خطاهای کمتری با استفاده از معیارهای MAPE, MAD و MSD گزارش می‌کند. هر مدلی که مقدار خطای کمتری داشت، آن مدل را بر داده‌های خود بپذیرید. در زمینه این مدل‌ها و فرمول به دست آوردن آن‌ها می‌توانید این لینک را ببینید.

4 همان‌گونه که قبلاً گفتیم Winters’ Method دارای سه جزء روند Trend، فصلی Seasonal و سطح Level است. به همین دلیل لازم است که این مدل سری زمانی دارای سه پارامتر به ازای هر کدام از اجزای مدل Winters باشد.

در بخش Weights to Use in Smoothing می‌توانیم اندازه‌های عددی هر کدام از پارامترها را انتخاب کرده و بنویسیم. توصیه می‌شود ابتدا تحلیل را بر مبنای وزن‌های پیش فرض نرم‌افزار انجام دهید. (به ازای هر کدام عدد 0.2 نوشته شده است.)

پس از بررسی نمودار سری زمانی حاصل، می‌توانید وزن‌ها را کم یا زیاد کنید. وزن‌های کمتر، خط صاف‌تر و هموارتری ایجاد می‌کنند و وزن‌های بیشتر، هموارسازی کمتری نتیجه می‌دهند. از وزن‌های کمتر برای داده‌های با نوسان و نویز بیشتر استفاده کنید اگر وزن‌ها را تنظیم کنید، تنظیم وزن جزء سطح معمولاً بهترین شانس را برای بهبود اندازه‌گیری های دقت Accuracy Measures دارد.

(Level) $ \displaystyle \alpha $

$ \displaystyle \alpha $ پارامتر مولفه سطح در Winters’ Method است و شبیه میانگین متحرک وزنی مشاهدات است. آلفا کمتر به داده‌های اخیر وزن کمتری می‌دهد و آلفا بالاتر وزن بیشتری به داده‌های اخیر می‌دهد.

همان‌گونه که در گراف مقابل می‌بینید، هر چقدر عدد قرار داده شده برای $ \displaystyle \alpha $ کمتر باشد، هموارسازی بیشتر خواهد بود و داده‌ةای برازش شده به صورت یک خط روند در می‌آیند. هر چقدر هم که عدد آلفا بیشتر باشد نوسان و نویز در داده‌های برازش شده بیشتر خواهد بود.

(Trend) $ \displaystyle \gamma $

$ \displaystyle \gamma $ پارامتر مولفه روند در Winters’ Method است و مشابه میانگین متحرک تفاوت بین مشاهدات متوالی است.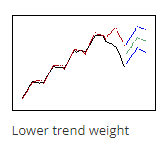

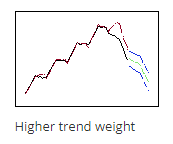
$\displaystyle \gamma $ کمتر وزن کمتری به داده‌های اخیر می‌دهد، بنابراین پیش‌بینی ها ( در تصویر مقابل یعنی نقاط سبز) از روند صعودی کلی داده‌ها پیروی می‌کنند.

اعداد بالاتر برای $\displaystyle \gamma $ وزن بیشتری به داده‌های اخیر می‌دهد، بنابراین پیش‌بینی ها از روند نزولی موجود در انتهای داده‌ها پیروی می‌کنند. در اینجا می‌توانید تصویر کناری را مشاهده کنید.

(Seasonal) $ \displaystyle \delta $

$ \displaystyle \delta $ وزنی است که به پارامتر فصلی Seasonal مدل Winters’ Method مربوط می‌شود. وزن کمتر به داده‌های اخیر وزن کمتری می‌دهد. وزن‌های بالاتر وزن بیشتری به داده‌های اخیر می‌دهد.

5 بخش Generate forecasts چنانچه بخواهیم پیش‌بینی برای گام‌های بعدی سری زمانی خود داشته باشیم، انتخاب می‌شود. از آن‌جا که به عنوان مثال هدف ما در این مطالعه این است که هزینه مصرف برق تا پنج ماه آینده را پیش‌بینی کنیم، بنابراین در کادر Number of forecasts عدد 5 را نوشته‌ایم.

کادر Starting from origin نیز چنانچه خالی گذاشته شود، به معنای این است که 5 گام پیش‌بینی بعدی از آخرین سطر داده‌ها یعنی سطر شماره 84 به بعد (85 تا 89) شروع شود. اگر در این کادر عددی را وارد کنید، نرم‌افزار Minitab از داده‌های تا آن شماره، جهت پیش‌بینی استفاده می‌کند. خوب است به این نکته دقت کنید که مقادیر پیش‌بینی Forecasts با برازش‌ها Fits متفاوت است زیرا Minitab از همه داده‌ها برای محاسبه برازش‌ها استفاده می‌کند.

6 در مرحله‌ی بعد وارد تب بشوید. در پنجره زیر گزینه‌های این تب را می‌بینید.

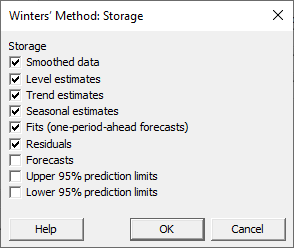
من گزینه‌های Smoothed data, Level estimates, Trend estimates, Seasonal estimates, Fits و Residuals را انتخاب کرده‌ام. این گزینه‌ها برای ما یافته‌های بیشتری از نتایج یعنی داده‌های هموار شده، براوردهای سطح، روند و فصلی، داده‌های برازش شده و باقیمانده‌ها را در شیت دیتا قرار می‌دهند.

نتایج آنالیز Winters’ Method

Results

هنگامی که OK می‌کنیم، نتایج و خروجی‌های زیر به دست می‌آید. در ادامه درباره‌ی آن‌ها صحبت می‌کنم.

در ابتدای نتایج، جدول با نام Model دیده می‌شود. تصویر زیر را ببینید.

آنچه از نتایج این جدول بر می‌آید این است که از مدل از نوع Additive Model استفاده شده است. تحلیل روند بر روی داده‌های ستون Electric Charges انجام شده و 84 سطر از داده‌ها (در این مثال یعنی 84 ماه)، مورد بررسی قرار گرفته است.

آنچه در مدل سری زمانی Winters’ Method به دنبال براورد آن بودیم، براورد ضرایب هموارسازی Smoothing Constants یعنی $ \displaystyle \alpha $ (ضریب سطح)، $\displaystyle \gamma $ (ضریب روند) و $\displaystyle \delta $ (ضریب فصلی) است. در جدول زیر این ضرایب به دست آمده است.

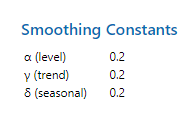
به این نکته دقت کنید که این ضرایب همان اعدادی است که ما در بخش Weights to Use in Smoothing تنظیمات نرم‌افزار وارد کردیم.

از آنجا که ما در تنظیمات نرم‌افزار و تب گزینه‌های نمایش داده‌های هموار شده، براوردهای سطح، روند و فصلی، داده‌های برازش شده و باقیمانده‌ها را انتخاب کردیم، بنابراین در شیت دیتا می‌توانید این نتایج را مشاهده کنید. در تصویر زیر بخشی از آن‌ها را آورده‌ام.

داده‌های مشاهده، هموار، براوردهای سطح، روند و فصلی، برازش شده و باقیمانده‌ها

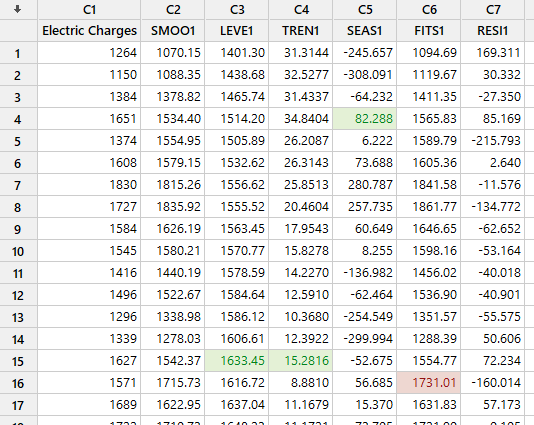
همان‌گونه که در داده‌های بالا مشاهده کنید به ازای هر کدام از داده‌های فروش مشاهده شده، عدد هموار شده SMOO، عدد براورد سطح LEVE، عدد براورد شده روند TREN و عدد براورد شده فصلی SEAS در ستون‌های جداگانه قرار گرفته است.

به همین ترتیب می‌توانید ستون مقدار برازش شده FITS را مشاهده کنیم. باقیمانده‌ها نیز اختلاف بین عدد مشاهده شده و عدد براورد شده است.

نکته خوب است این نکته را بدانیم که عدد براورد شده در هر تایم، مجموع اعداد هموار شده سطح LEVE، براورد شده روند TREN در تایم قبل و براورد شده فصلی SEAS در تایم t-p است. p در اینجا همان طول دوره فصلی است که در تنظیمات نرم‌افزار در بخش Seasonal length قرار می‌گیرد. ما در این مثال عدد p را برابر با 12 در نظر گرفتیم.

بنابراین به عبارت ساده در یک مدل Additive، براورد سری زمانی در تایم t به صورت زیر به دست می‌آید.

$ \displaystyle {{\hat{Y}}_{t}}={{L}_{{t-1}}}+{{T}_{{t-1}}}+{{S}_{{t-p}}}$

به عنوان مثال به جدول داده‌های تصویر بالا نگاه کنید. عدد براورد شده در سطر 16 یعنی t=16 از مجموع اعداد سطح و روند در تایم 15 و فصلی در تایم 4 (4=12-16) به دست می‌آید.

مدل سری زمانی به دست آمده مانند هر مدل رگرسیونی دیگر (سری زمانی نوعی رگرسیون است)، دارای معیارهایی جهت بررسی مناسب بودن مدل است. هنگامی که از Winters’ Method استفاده می‌کنیم، با معیارهای زیر روبه‌رو هستیم.

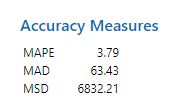
از آن‌جا که این معیارها از جنس خطا هستند، بنابراین هرچقدر اندازه عددی آن‌ها کمتر باشد، بیانگر مناسب بودن مدل سری زمانی به دست آمده است. هر یک از این معیارها به صورت زیر محاسبه می‌شوند.

در این زمینه علاقمند بودید، می‌توانید این لینک را ببینید.

Mean Absolute Percent Error (MAPE)

$ \displaystyle MAPE=\frac{1}{n}\sum\limits_{{t=1}}^{n}{{\frac{{\left| {{{y}_{t}}-{{{\hat{y}}}_{t}}} \right|}}{{{{y}_{t}}}}}}\times 100=\frac{1}{n}\sum\limits_{{t=1}}^{n}{{\frac{{\left| {{{e}_{t}}} \right|}}{{{{y}_{t}}}}}}\times 100$

(Mean Absolute Deviation) MAD

$ \displaystyle MAD=\frac{1}{n}\sum\limits_{{t=1}}^{n}{{\left| {{{y}_{t}}-{{{\hat{y}}}_{t}}} \right|=}}\frac{1}{n}\sum\limits_{{t=1}}^{n}{{\left| {{{e}_{t}}} \right|}}$

(Mean Square Deviation) MSD

$ \displaystyle MSD=\frac{1}{n}\sum\limits_{{t=1}}^{n}{{{{{\left| {{{y}_{t}}-{{{\hat{y}}}_{t}}} \right|}}^{2}}=}}\frac{1}{n}\sum\limits_{{t=1}}^{n}{{{{{\left| {{{e}_{t}}} \right|}}^{2}}}}$

همان‌گونه که در ابتدا بیان کردم، به دنبال پیش‌بینی مقدار فروش برای پنج ماه آینده نیز هستیم. در جدول زیر با نام Forecasts این نتایج به دست آمده است.

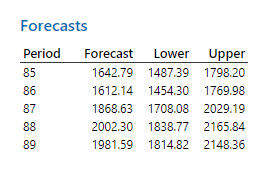
از آن‌جا که مطالعه ما دارای 84 سطر بود (بررسی فروش ماهانه در 7 سال)، بنابراین نرم افزار برای دوره‌های زمانی 85 تا 89 پیش‌بینی خود را بر مبنای مدل Winters' Method انجام داده است. نکته جالب توجه این است که این پیش‌بینی‌ها شامل فواصل اطمینان 95 درصد نیز می‌باشد.

در گراف زیر که نمودار سری زمانی داده‌های فروش بر مبنای Winters' Method است، مشاهده می‌شود.

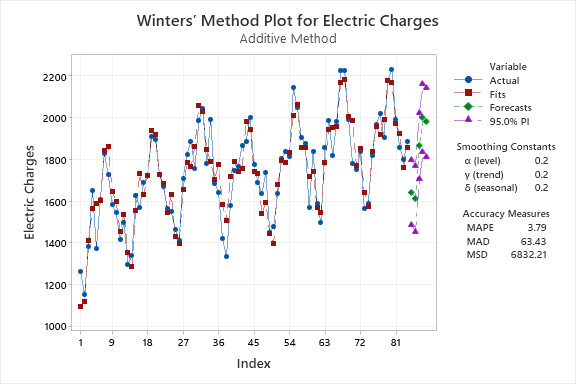
در این گراف نقاط آبی داده‌های واقعی فروش، نقاط قرمز رنگ اندازه‌های براورد شده بر مبنای تحلیل Winters’ Method، نقاط سبر رنگ پیش‌بینی مدل برای فروش در پنج ماه آینده و نقاط بنفش فواصل اطمینان پیش‌بینی‌ها می‌باشد.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2023). Winters' Method with Minitab software. Statistical tutorial and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/winters-method-minitab/.php

For example, if you viewed this guide on 12^th January 2023, you would use the following reference

GraphPad Statistics (2023). Winters' Method with Minitab software. Statistical tutorials and software guides. Retrieved January, 12, 2023, from https://graphpad.ir/winters-method-minitab/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.

سبد خرید