هموارسازی نمایی دوگانه Double Exponential Smoothing با نرمافزار Minitab
Double Exponential Smoothing
به منظور هموار کردن دادهها با محاسبه میانگینهای وزنی نمایی و ارایه پیشبینی های کوتاه مدت، هنگامی که دادهها دارای روند هستند، از هموارسازی نمایی دوگانه استفاده میشود. دربارهی مفهوم هموارسازی هم توضیح اینکه این کار جهت حذف نوسان و نویز در مجموعه دادهها انجام میشود. ایده هموارسازی این است که میتواند پراکندگیهای ساده شده موجود در دادهها را شناسایی کند و به پیشبینی الگوهای مختلف کمک کند. در بازارهای مالی، نویز میتواند شامل اصلاحات کوچک قیمت در بازار و همچنین نوسانات قیمت باشد که روند کلی دادهها را مخدوش میکند.
هموارسازی نمایی اولین بار توسط رابرت گودل براون در سال 1956 پیشنهاد شد و سپس توسط چارلز سی. هولت در سال 1957 گسترش یافت.
همانطور که میدانیم، در میانگین متحرک ساده، مشاهدات گذشته به طور مساوی وزن داده میشوند، با این حال در مدل سری زمانی Exponential Smoothing از توابع نمایی برای تخصیص وزن در طول زمان استفاده میشود.
این روش به عنوان هموارسازی تصحیح شده هولت Holt’s trend corrected یا هموارسازی نمایی مرتبه دوم نیز نامیده میشود و از آن برای پیشبینی سریهای زمانی، هنگامی که دادهها روند خطی دارند و البته فاقد الگوی فصلی هستند، استفاده میشود. ایده اصلی هموارسازی نمایی دوگانه، معرفی یک پارامتر جهت در نظر گرفتن روند در سری دادههای هموار شده است.
فرمول محاسبه Double Exponential Smoothing
Formula
همانگونه که از نام این نوع مدلهای سری زمانی برمیآید، در Double Exponential Smoothing با دو پارامتر یکی برای هموارسازی با نام $ \displaystyle \alpha $ که به آن Smoothing Factor و دیگری با نام $\displaystyle \gamma $ که به آن Trend Smoothing Factor گفته میشود، روبهرو هستیم.
جهت فهم بهتر مطلب و اینکه در مدل هموار سازی نمایی دوگانه که ما در این مقاله از آن حرف میزنیم، چه اتفاقی میافتد، ابتدا بیایید به فرمول به دست آوردن دادههای هموار شده Data Smoothing و روند هموار شده Trend Smoothing بپردازیم. در رابطهی زیر، فرمول محاسبه آنها آمده است.
$ \displaystyle \begin{array}{l}{{S}_{t}}=\alpha {{Y}_{t}}+\left( {1-\alpha } \right)\left( {{{S}_{{t-1}}}+{{b}_{{t-1}}}} \right)\\\\{{b}_{t}}=\gamma \left( {{{S}_{t}}-{{S}_{{t-1}}}} \right)+\left( {1-\gamma } \right){{b}_{{t-1}}}\\\\{{{\hat{Y}}}_{t}}={{S}_{{t-1}}}+{{b}_{{t-1}}}\end{array}$
در این رابطه $\displaystyle {{S}_{t}}$ داده هموار شده در زمان $ \displaystyle t$ است که به صورت میانگین وزنی از مشاهده $\displaystyle {{Y}_{t}}$ تعریف میشود. همچنین $ \displaystyle {{S}_{{t-1}}}$ مشاهده قبلی هموار شده در زمان $ \displaystyle t-1$ تعریف میشود.
به همین ترتیب $ \displaystyle {{b}_{t}}$ عدد ترند براورد شده در زمان $ \displaystyle t$ و $ \displaystyle {{b}_{t-1}}$ عدد Trend براورد شده در زمان $ \displaystyle t-1$ است.
در نهایت در یک مدل Double Exponential Smoothing مقدار براورد شده سری در زمان t یعنی $ \displaystyle {{{\hat{Y}}}_{t}}$ از مجموع مقادیر عددی هموار شده $ \displaystyle \left( {{{S}_{{t-1}}}} \right)$ و ترند شده $ \displaystyle \left( {{{b}_{{t-1}}}} \right)$ در زمان t-1 به دست میآید.
به این ترتیب بیان میشود که هموارسازی نمایی دوگانه از یک بخش سطح level component (در فرمول بالا یعنی $ \displaystyle {{S}_{{t-1}}}$) و یک بخش روند trend component (در فرمول بالا یعنی $ \displaystyle {{b}_{{t-1}}}$) در هر تایم استفاده میکند. این نوع مدل سری زمانی از دو پارامتر وزن (که پارامترهای هموارسازی نیز نامیده میشوند) جهت براورد عدد سری، استفاده میکند.
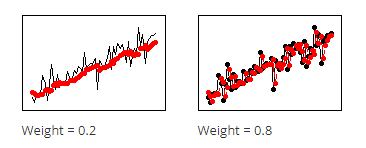
$ \displaystyle \alpha $ (Level)$ \displaystyle \alpha $ در این رابطه به عنوان فاکتور هموار سازی دادهها، نام برده میشود. $ \displaystyle \alpha $ عددی بین صفر تا یک است. بر مبنای تعریف فرمول بالا، هر چقدر $ \displaystyle \alpha $ بزرگتر باشد، وزن بیشتری به داده واقعی در همان زمان میدهد. در تعریف نوشته شده $ \displaystyle \alpha {{Y}_{t}}$ و از این جهت دادهها کمتر هموار میشوند. به گرافهای زیر نگاه کنید.
$ \displaystyle \gamma $ (Trend)
در یک مدل هموارسازی نمایی دوگانه با فاکتور دیگری با نام $\displaystyle \gamma $ که به آن Trend Smoothing Factor گفته میشود، روبهرو هستیم.
$\displaystyle \gamma $ وزنی است که در جزء روند برآورد هموار شده استفاده میشود. $\displaystyle \gamma $ مشابه میانگین متحرک تفاوت بین مشاهدات متوالی است.
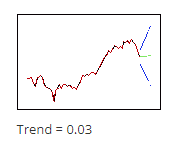
$\displaystyle \gamma $ کمتر وزن کمتری به دادههای اخیر میدهد، بنابراین پیشبینی ها ( در تصویر مقابل یعنی نقاط سبز) از روند کلی دادهها پیروی میکنند.
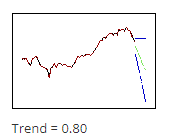
اعداد بالاتر برای $\displaystyle \gamma $ وزن بیشتری به دادههای اخیر میدهد، بنابراین پیشبینی ها از روند موجود در انتهای دادهها پیروی میکنند. در اینجا میتوانید تصویر کناری را مشاهده کنید.
نکتهای که وجود دارد این است که هیچ روش رسمی دقیقی برای انتخاب هموارسازی نمایی دوگانه یعنی $ \displaystyle \alpha $ و $\displaystyle \gamma $ وجود ندارد. گاهی اوقات تصمیم محقق برای انتخاب آلفا و گاما، در نظر گرفته میشود.
با این حال چنانچه نظر و ایدهای جهت قرار دادن عدد خاصی برای آلفا و گاما نداشته باشیم، میتوان از یک تکنیک آماری جهت بهینهسازی مقدار $ \displaystyle \alpha $ و $\displaystyle \gamma $ استفاده کرد. برای مثال، روش حداقل مربعات برای تعیین مقدار $ \displaystyle \alpha $ که مجموع مربعات خطا (اختلاف بین عدد واقعی با عدد پیشبینی شده) را به حداقل میرساند، استفاده میشود.
از آنجا که در این مقاله قصد داریم به تحلیل هموارسازی نمایی دوگانه با استفاده از نرمافزار Minitab بپردازیم، هر کدام از روشهای بالا یعنی انتخاب محقق و یا انتخاب بهینه نرمافزار، در تنظیمات تحلیل قرار دارد که در ادامه و در بخشهای بعدی به آنها اشاره میکنیم.
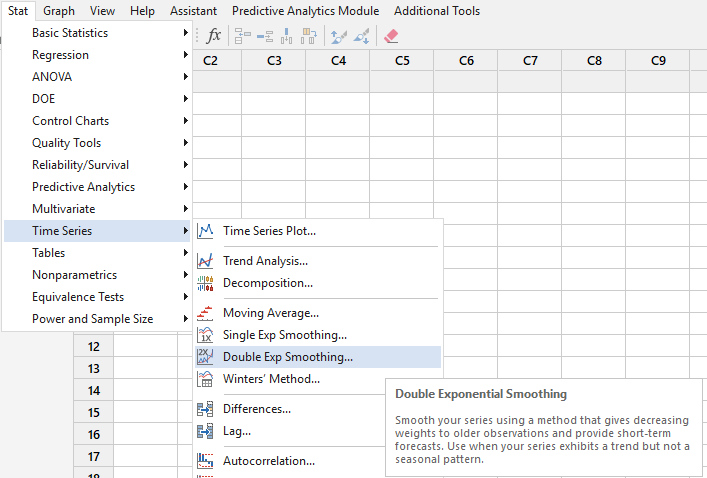
جهت انجام تحلیل Double Exponential Smoothing، از مسیر زیر در نرمافزار Minitab استفاده میکنیم.
Stat → Time Series → Double Exponential Smoothing
تحلیلهای جایگزین. اگر دادههای شما فاقد روند هستند و جز فصلی Seasonal Component ندارند، از میانگین متحرک Moving Average یا هموارسازی نمایی منفرد Single Exponential Smoothing استفاده کنید.
اگر دادههای شما دارای اثر فصلی، با یا بدون روند هستند، از تحلیل Decomposition یا Winters’ Method استفاده کنید.
مثال آنالیز Double Exponential Smoothing
Example
یک فروشنده آنلاین میخواهد فروش محصول کامپیوتر را برای سه ماه آینده پیشبینی کند. این فرد دادههای مربوط به فروش رایانه و نرمافزار را از دو سال گذشته جمعآوری میکند تا بتواند روندهای آینده را پیشبینی کند.
فایل دیتا این مثال را میتوانید از اینجا Double Exponential Smoothing دریافت کنید. در تصویر زیر بخشی از دادهها را مشاهده میکنید.
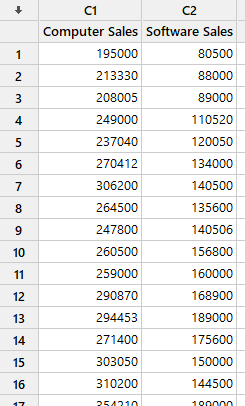
خوب است در ابتدا یک نمودار سری زمانی از دادههای مثال رسم کنیم. این کار به ما کمک میکند تا درکی از دادههای مورد مطالعه داشته باشیم. علاقمند بودید میتوانید در لینک (رسم نمودارهای سری زمانی Time Series Plot) با انواع گرافهای سری زمانی در نرمافزار Minitab آشنا شوید.
در تصویر زیر، من گراف سری زمانی دادههای فروش محصول کامپیوتر را آوردهام.
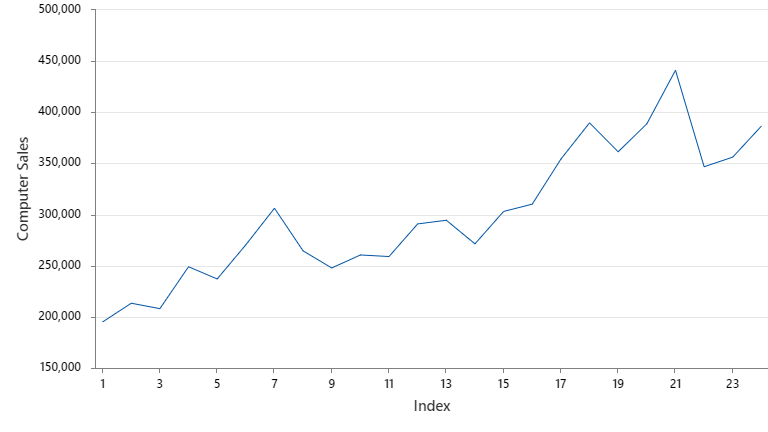
همانگونه که در گراف سری زمانی میزان فروش محصول دیده میشود، دادهها فاقد روند و یا اثر فصلی دوره تناوب هستند. بنابراین به نظر میرسد استفاده از مدل سری زمانی هموارسازی نمایی منفرد، جهت برازش مدل بر دادهها، مناسب باشد.
از مسیر زیر آنالیز Single Exponential Smoothing در نرمافزار Minitab انجام میشود.
در این صورت پنجره زیر با نام Double Exponential Smoothing برای ما باز میشود.
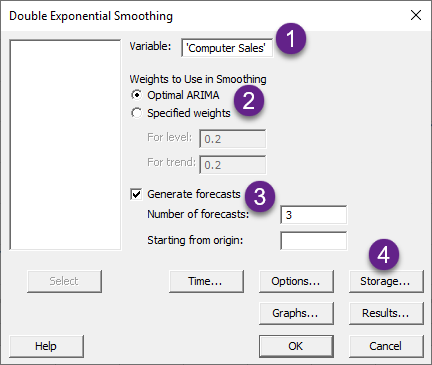
من پنجره بالا را شمارهگزاری کردهام و در ادامه به ترتیب شمارهها به توضیح هر بخش میپردازم.
1 ستون با نام Computer Seles که بیانگر میزان فروش کامپیوتر در هر ماه است، در کادر Variable قرار میگیرد.
2 در این بخش که با نام Weight to Use in Smoothing قرار دارد، به تعیین عدد پارامترهای $ \displaystyle \alpha $ و $\displaystyle \gamma $ که وزن دادهها جهت هموارسازی را تعیین میکنند، میپردازیم. در این زمینه قبلاً بیشتر صحبت کردیم.
نرمافزار Minitab به یکی از روشهای Optimal ARIMA و دیگری Specified weight یعنی انتخاب کاربر، عدد پارامترهای $ \displaystyle \alpha $ و $\displaystyle \gamma $ را تعیین میکند. معمولاً توصیه میشود انتخاب وزن آلفا و گاما را به عهدهی خود نرمافزار قرار دهیم و گزینهی Optimal ARIMA را که پیشفرض نرمافزار است، انتخاب کنیم.
البته چنانچه ایده و یا تجربه قبلی، جهت وزن دلخواه خود برای هموار کردن دادهها دارید، میتوانید عدد آن را در کادر For level برای پارامتر $ \displaystyle \alpha $ و For trend برای پارامتر $\displaystyle \gamma $ بنویسید. این اعداد باید بین صفر تا یک باشد.
اگر هم ایدهای دربارهی عدد $ \displaystyle \alpha $ و $\displaystyle \gamma $ ندارید، گزینهی Optimal ARIMA را انتخاب کنید. سپس، پس از بررسی نمودار سری زمانی به دست آمده، میتوانید عدد آلفا یا گاما را کم یا زیاد کنید.
همانگونه که قبلاً گفتیم برای $ \displaystyle \alpha $ عددهای کمتر، خط صافتر و هموارسازی بیشتری ایجاد میکنند و عددهای بالاتر، هموارسازی کمتری درست میکنند. از عددهای $ \displaystyle \alpha $ کمتر برای دادههای که نوسان و نویز بیشتری دارند استفاده کنید تا مقادیر هموار شده با نویز نوسان نکنند.
همچنین اعداد $\displaystyle \gamma $ کمتر وزن کمتری به دادههای آخر سری میدهد، بنابراین پیشبینی ها از روند کلی دادهها پیروی میکنند و اعداد بالاتر $\displaystyle \gamma $ وزن بیشتری به دادههای اخیر میدهد، بنابراین پیشبینی ها از روند موجود در انتهای دادهها پیروی میکنند.
سوال شاید این سوال پیش بیاید که Optimal ARIMA چیست و نرمافزار چگونه با استفاده از این گزینه به محاسبه $ \displaystyle \alpha $ و $\displaystyle \gamma $ میپردازد؟
همانگونه که قبلاً نیز گفتیم، نرمافزار آن مقدار $ \displaystyle \alpha $ و $\displaystyle \gamma $ را انتخاب میکند که به ازای آن، مجموع مربعات خطای مدل سری زمانی، مینیمم و کمترین شود. یعنی SSE که از رابطهی زیر به دست میآید، مینیمم شود.
$ \displaystyle SSE=\sum\limits_{{t=1}}^{n}{{{{{\left( {{{y}_{t}}-{{{\hat{y}}}_{t}}} \right)}}^{2}}}}=\sum\limits_{{t=1}}^{n}{{{{{\left( {{{e}_{t}}} \right)}}^{2}}}}$
به عبارت دیگر آن مقدار آلفا و گامایی توسط نرمافزار در نظر گرفته میشود که مجموع توان دوم اختلاف هر مشاهده با براورد ناشی از مدل سری زمانی آن (یعنی همان مدل Optimal ARIMA)، کمترین مقدار شده باشد.
همین جا یک سوال دیگری پیش میآید. کدام مدل سری زمانی؟ Optimal ARIMA که نرمافزار از آن نام میبرد، کدام نوع مدل سری زمانی است؟ شما که هنوز مدلی براورد نکردهای و در نتیجه $ \displaystyle {{{{\hat{y}}}_{t}}}$ هنوز معلوم نیست. فقط $ \displaystyle {{{y}_{t}}}$ در اختیار ما است.
پاسخ این سوال که راز نحوهی به دست آوردن $ \displaystyle \alpha $ و $\displaystyle \gamma $ را نیز برای ما معلوم میکند این است که نرمافزار Minitab جهت براورد آلفا و گاما بهینه از یک مدل سری زمانی با نام ARIMA (0, 2, 2) استفاده میکند. در واقع $ \displaystyle {{{{\hat{y}}}_{t}}}$ براورد دادهها از این مدل سری زمانی است.
یک مدل سری زمانی ARIMA (0, 2, 2) به صورت زیر نوشته میشود. در زمینه درک بهتر مدلهای سری زمانی ARIMA این لینک را ببینید.
$ \displaystyle {{Y}_{t}}=2{{Y}_{{t-1}}}-{{Y}_{{t-2}}}+\left( {\alpha +\beta -2} \right){{\varepsilon }_{{t-1}}}+\left( {1-\alpha } \right){{\varepsilon }_{{t-2}}}+{{\varepsilon }_{t}}$
در این رابطه $ \displaystyle {{\varepsilon }_{t}}$ به عنوان مقدار خطای پیشبینی در زمان t تعریف میشود.
3 بخش Generate forecasts چنانچه بخواهیم پیشبینی برای گامهای بعدی سری زمانی خود داشته باشیم، انتخاب میشود. از آنجا که به عنوان مثال هدف ما در این مطالعه این است که تا سه ماه آینده را پیشبینی کنیم، بنابراین در کادر Number of forecasts عدد 3 را نوشتهایم.
کادر Starting from origin نیز چنانچه خالی گذاشته شود، به معنای این است که 3 گام پیشبینی بعدی از آخرین سطر دادهها یعنی سطر شماره 24 به بعد (25 تا 27) شروع شود. اگر در این کادر عددی را وارد کنید، نرمافزار Minitab از دادههای تا آن شماره، جهت پیشبینی استفاده میکند. خوب است به این نکته دقت کنید که مقادیر پیشبینی Forecasts با برازشها Fits متفاوت است زیرا Minitab از همه دادهها برای محاسبه برازشها استفاده میکند.
4 در مرحلهی بعد وارد تب ![]() بشوید. در پنجره زیر گزینههای این تب را میبینید.
بشوید. در پنجره زیر گزینههای این تب را میبینید.
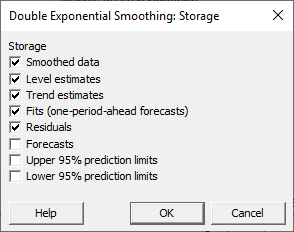
من گزینههای Smoothed data, Level estimates, Trend estimates, Fits و Residuals را انتخاب کردهام. این گزینهها برای ما یافتههای بیشتری از نتایج یعنی دادههای هموار شده، براوردهای سطح و روند، دادههای برازش شده و باقیماندهها را در شیت دیتا قرار میدهند.
نتایج آنالیز هموارسازی نمایی دوگانه
Results
هنگامی که OK میکنیم، نتایج و خروجیهای زیر به دست میآید. در ادامه دربارهی آنها صحبت میکنم.
در ابتدای نتایج، جدول با نام Model دیده میشود. تصویر زیر را ببینید.
آنچه از نتایج این جدول بر میآید این است که تحلیل هموارسازی نمایی دوگانه بر روی دادههای ستون Sales انجام شده و 24 سطر از دادهها (در این مثال یعنی 24 ماه) مورد بررسی قرار گرفته است.
آنچه در مدل سری زمانی هموارسازی نمایی دوگانه به دنبال براورد آن بودیم، ضرایب هموارسازی Smoothing Constants یعنی $ \displaystyle \alpha $ (ضریب سطح) و $\displaystyle \gamma $ (ضریب روند) است. در جدول مقابل این ضرایب به دست آمده است.
عدد براورد شده آلفا با استفاده از مدل ARIMA (0, 2, 2) که به آن اشاره کردیم، برابر با 0.599 شده است. این عدد نشان میدهد بخش سطح level component مدل Double Exponential Smoothing به دست آمده در این مثال به صورت زیر خواهد بود.
$ \displaystyle {{S}_{t}}=0.6{{Y}_{t}}+0.4\left( {{{S}_{{t-1}}}+{{b}_{{t-1}}}} \right)$
به همین ترتیب عدد براورد شده گاما با استفاده از مدل ARIMA (0, 2, 2) که به آن اشاره کردیم، برابر با 0.131 به دست آمده است. این عدد نشان میدهد بخش روند Trend component مدل هموارسازی نمایی دوگانه صورت زیر خواهد بود.
$\displaystyle {{b}_{t}}=0.13\left( {{{S}_{t}}-{{S}_{{t-1}}}} \right)+0.87{{b}_{{t-1}}}$
با استفاده از رابطهی بالا، عدد براورد شده برای هر تایم t به صورت زیر به دست میآید.
$ \displaystyle {{{\hat{Y}}}_{t}}=\left( {{{S}_{{t-1}}}} \right)+\left( {{{b}_{{t-1}}}} \right)$
این مطلب به معنای آن است که مقدار برازش شده در هر زمان، مجموع مقادیر بخش سطح $ \displaystyle {{{S}_{{t-1}}}}$ و بخش روند $ \displaystyle {{{b}_{{t-1}}}}$ در زمان قبل است.
از آنجا که ما در تنظیمات نرمافزار و تب ![]() گزینههای نمایش دادههای هموار شده، براوردهای سطح و روند، دادههای برازش شده و باقیماندهها را انتخاب کردیم، بنابراین در شیت دیتا میتوانید این نتایج را مشاهده کنید. در تصویر زیر بخشی از آنها را آوردهام.
گزینههای نمایش دادههای هموار شده، براوردهای سطح و روند، دادههای برازش شده و باقیماندهها را انتخاب کردیم، بنابراین در شیت دیتا میتوانید این نتایج را مشاهده کنید. در تصویر زیر بخشی از آنها را آوردهام.
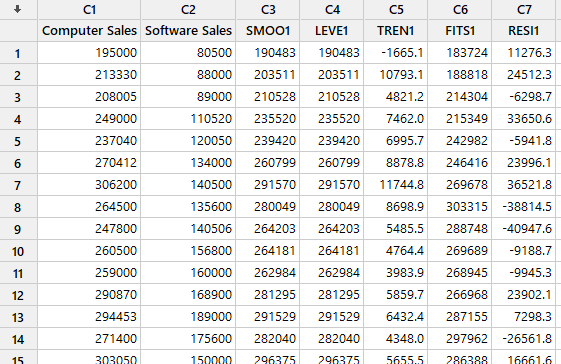
همانگونه که در دادههای بالا مشاهده کنید به ازای هر کدام از دادههای فروش مشاهده شده، عدد هموار شده SMOO، عدد براورد سطح LEVE (آنها در یک مدل سری زمانی هموارسازی نمایی دوگانه، یکسان هستند) و عدد براورد شده روند TREN در یک ستون جداگانه قرار گرفته است.
به همین ترتیب میتوانید ستون مقدار برازش شده FITS را مشاهده کنیم. همانگونه که قبلاً گفتیم عدد براورد شده در هر تایم، مجموع اعداد هموار شده سطح LEVE و براورد شده روند TREN در تایم قبل است. به عبارت ساده رابطهی FITS (t) = LEVE (t-1) + TREN (t-1) برقرار است.
باقیماندهها نیز اختلاف بین عدد مشاهده شده و عدد براورد شده است.
مدل سری زمانی به دست آمده مانند هر مدل رگرسیونی دیگر (سری زمانی نوعی رگرسیون است)، دارای معیارهایی جهت بررسی مناسب بودن مدل است. هنگامی که از هموارسازی نمایی دوگانه استفاده میکنیم، با معیارهای زیر در جدول Accuracy Measures روبهرو هستیم.

از آنجا که این معیارها از جنس خطا هستند، بنابراین هرچقدر اندازه عددی آنها کمتر باشد، بیانگر مناسب بودن مدل سری زمانی به دست آمده است. هر یک از این معیارها به صورت زیر محاسبه میشوند.
در این زمینه علاقمند بودید، میتوانید این لینک را ببینید.
-
- Mean Absolute Percent Error (MAPE)
- (Mean Absolute Deviation) MAD
- (Mean Square Deviation) MSD
$ \displaystyle MAPE=\frac{1}{n}\sum\limits_{{t=1}}^{n}{{\frac{{\left| {{{y}_{t}}-{{{\hat{y}}}_{t}}} \right|}}{{{{y}_{t}}}}}}\times 100=\frac{1}{n}\sum\limits_{{t=1}}^{n}{{\frac{{\left| {{{e}_{t}}} \right|}}{{{{y}_{t}}}}}}\times 100$
$ \displaystyle MAD=\frac{1}{n}\sum\limits_{{t=1}}^{n}{{\left| {{{y}_{t}}-{{{\hat{y}}}_{t}}} \right|=}}\frac{1}{n}\sum\limits_{{t=1}}^{n}{{\left| {{{e}_{t}}} \right|}}$
$ \displaystyle MSD=\frac{1}{n}\sum\limits_{{t=1}}^{n}{{{{{\left| {{{y}_{t}}-{{{\hat{y}}}_{t}}} \right|}}^{2}}=}}\frac{1}{n}\sum\limits_{{t=1}}^{n}{{{{{\left| {{{e}_{t}}} \right|}}^{2}}}}$
همانگونه که در ابتدا بیان کردم، به دنبال پیشبینی مقدار فروش برای سه ماه آینده نیز هستیم. در جدول زیر با نام Forecasts این نتایج به دست آمده است.
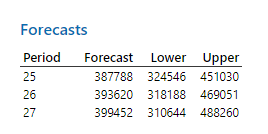
از آنجا که مطالعه ما دارای 24 سطر بود (بررسی فروش محصول کامپیوتر در 2 سال)، بنابراین نرم افزار برای دورههای زمانی 25 تا 27 پیشبینی خود را بر مبنای مدل Double Exponential Smoothing انجام داده است. نتیجه به دست آمده نشان میدهد که میزان فروش با 95% اطمینان، در این سه ماه میتواند در بازهای از 31 تا حدود 49 هزار واحد قرار گیرد.
در گراف زیر که نمودار سری زمانی دادههای فروش بر مبنای مدل هموارسازی نمایی دوگانه است، مشاهده میشود.
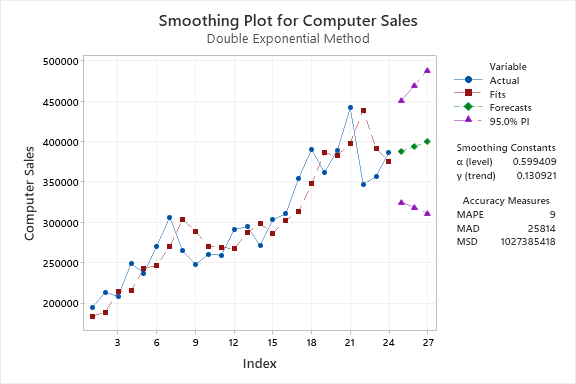
در این گراف نقاط آبی دادههای واقعی فروش، نقاط قرمز رنگ اندازههای براورد شده بر مبنای تحلیل Double Exponential Smoothing و سه نقطه سبز رنگ همراه با فواصل اطمینان 95% بنفش رنگ، نیز پیشبینی مدل برای فروش در سه ماه آینده میباشد.
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2023). Double Exponential Smoothing with Minitab software. Statistical tutorial and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/double-exponential-smoothing-minitab/.php
For example, if you viewed this guide on 12th January 2023, you would use the following reference
GraphPad Statistics (2023). Double Exponential Smoothing with Minitab software. Statistical tutorials and software guides. Retrieved January, 12, 2023, from https://graphpad.ir/double-exponential-smoothing-minitab/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.