نتایج و خروجی های تحلیل رگرسیون خطرات متناسب کاکس
Cox Proportional Hazards Regression (Results)
در مقاله (رگرسیون خطرات متناسب کاکس Cox Proportional Hazards Regression چیست؟) به بررسی این نوع از تحلیلهای آنالیز بقا با استفاده از نرمافزار Prism پرداختیم. در آنجا دربارهی ورود دادهها به نرمافزار، بیان مثال، تنظیمات، تبها و گزینههای مختلف موجود در نرمافزار جهت اجرای رگرسیون کاکس، اشاره کردیم.
در این مقاله میخواهم به صورت جداگانه به بیان خروجیها و نتایج کامل نرمافزار Prism هنگامی که برای ما رگرسیون خطرات متناسب کاکس را انجام میدهد، بپردازم. بنابراین ابتدا توصیه میکنم مقاله (رگرسیون خطرات متناسب کاکس Cox Proportional Hazards Regression چیست؟) را بخوانید و سپس اقدام به مطالعه این مقاله نمایید.
فایل دیتا این مثال را میتوانید از اینجا دریافت کنید.
نتایج رگرسیون خطرات متناسب کاکس
Results & Graphs
پس از بررسی تبهای موجود در پنجره Parameters: Multiple Cox Regression دکمه OK را میزنیم. ما اکثر گزینههای پیشفرض را که نرمافزار Prism ارایه میدهد، به دست میآوریم. در ادامه دربارهی نتایج و گرافهای به دست آمده از تحلیل رگرسیون کاکس بیشتر صحبت میکنیم.
در برگهی نتایج Results نرمافزار میتوانیم خروجیهای رگرسیون کاکس را ببینیم. در ابتدا برگه با نام Tabular results دیده میشود. نتایج این برگه در چند بخش اصلی بیان شده است. در ادامه به ترتیب به توضیح هر یک میپردازیم.
- Parameter estimates
در این بخش، براورد پارامترهای رگرسیون کاکس آمده است. تصویر زیر بخشی از این نتایج است.
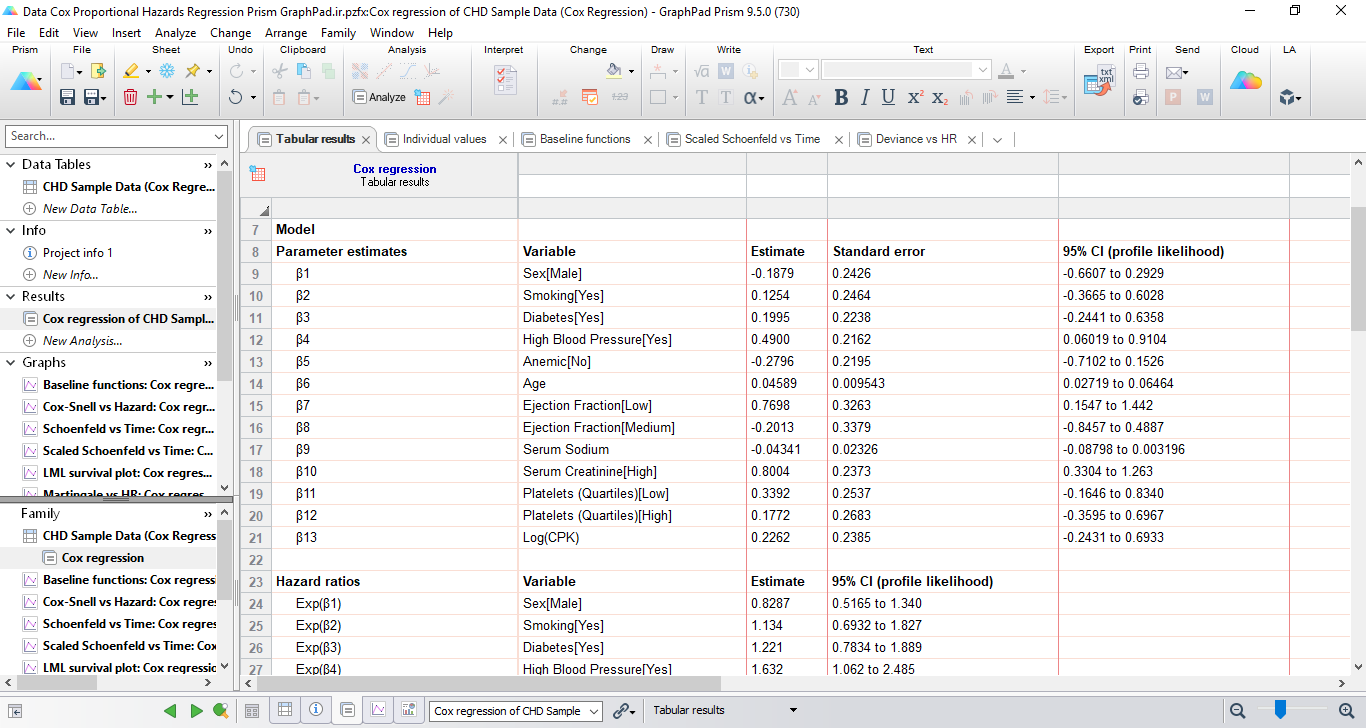
در جدول بالا ضرایب رگرسیون (ضرایب بتا) مدل به ازای هر کدام از کمیتةای مستقل، مشخص شده است. توجه داشته باشید که برخلاف برخی دیگر از تکنیکهای رگرسیون چندگانه، رگرسیون خطرات متناسب کاکس شامل یک ضریب ثابت (β0) نمیشود. علاوه بر این توجه داشته باشید که وقتی Variable های طبقهبندی در مدل قرار میگیرند، به طور خودکار "کدسازی ساختگی" میشوند و در نتیجه یک براورد پارامتر جداگانه برای هر سطح از کمیت طبقهبندی به غیر از سطح رفرنس ایجاد میشود. بنابراین، نتایج برای مدل ما شامل سیزده ضریب بتا جداگانه است که در تصویر بالا نشان داده شده است.
تفسیر براورد پارامترهای به دست آمده، کمی متفاوت از رگرسیون خطی چندگانه استاندارد است. مدل خطرات متناسب کاکس این مثال را میتوان به صورت زیر نوشت.
$\displaystyle \begin{array}{l}h\left( t \right)={{h}_{0}}\left( t \right)\times \exp \left\{ {\left( {Sex\left[ {Male} \right]\times {{\beta }_{1}}} \right)+\left( {Smoking\left[ {Yes} \right]\times {{\beta }_{2}}} \right)+....+\left( {LogCPK\times {{\beta }_{{13}}}} \right)} \right\}\\\to \\\frac{{h\left( t \right)}}{{{{h}_{0}}\left( t \right)}}=\exp \left\{ {\left( {Sex\left[ {Male} \right]\times {{\beta }_{1}}} \right)+\left( {Smoking\left[ {Yes} \right]\times {{\beta }_{2}}} \right)+....+\left( {LogCPK\times {{\beta }_{{13}}}} \right)} \right\}\\\to \\\ln \left( {\frac{{h\left( t \right)}}{{{{h}_{0}}\left( t \right)}}} \right)=\left( {Sex\left[ {Male} \right]\times {{\beta }_{1}}} \right)+\left( {Smoking\left[ {Yes} \right]\times {{\beta }_{2}}} \right)+....+\left( {LogCPK\times {{\beta }_{{13}}}} \right)\end{array}$
با استفاده از این رابطه، میتوان مشاهده کرد که سمت چپ معادله، گزارشی از نسبت نرخ خطر برای یک فرد یا گروه خاص است (با استفاده از کمیتهای پیشبینی کننده خاص که مربوط به این فرد یا گروه است. )، تقسیم بر خطر خط پایه (که نشان دهنده نرخ خطر زمانی است که همه کمیتهای پیشبینی بر روی صفر یا مقدار رفرنس آنها تنظیم میشوند).
با دانستن این موضوع، میتوانیم ببینیم که مقدار ضریب بتا نشاندهنده افزایش (برای مقادیر مثبت) یا کاهش (برای مقادیر منفی) در لگاریتم نرخ خطر است. به عنوان مثال، در نتایج ما، β1 (جنس [مرد]) برابر با 0.1879- است. این بدان معناست که در مقایسه با زنان، لگاریتم نرخ خطر برای مردان در تمام نقاط زمانی 0.1879 کاهش مییابد. مقدار β6 (سن) 0.04589 است. این بدان معنی است که به ازای هر سال افزایش سن یک فرد، لگاریتم نرخ خطر 0.04589 افزایش پیدا میکند.
سایر نتایج مانند خطای استاندارد standard error و فواصل اطمینان 95% برای مقادیر براورد شده رگرسیونی را میتوانید در جدول بالا، مشاهده کنید.
- Hazard ratios
شاید بتوان گفت مهمترین یافته و نتیجهای که از رگرسیون کاکس به دست میآید همین نسبت خطر HR است. تفسیر مستقیم ضرایب بتا پیچیده است زیرا این ضرایب مربوط به لگاریتم نرخ خطر است، در حالی که درک مقیاس خطی در مقایسه با مقیاس لگاریتمی به طور کلی آسانتر است. به این ترتیب، بخش بعدی نتایج، نسبتهای خطر است. در تصویر زیر آن را ببینید.

نتایج کاملتر از رابطه بین براورد پارامترها و نسبتهای خطر را میتوان در اینجا یافت. نسبت خطر HR نشان میدهد هنگامی که کمیت پیشبینی کننده یک واحد افزایش مییابد، HR چند برابر بیشتر (یا کوچکتر) میشود. در مثال بالا، میبینیم که نسبت خطر Age برابر با 1.047 است. این بدان معناست که به ازای هر سال افزایش سن، نسبت خطر آنها مضربی از 1.047 افزایش مییابد. از نظر ریاضی، نسبتهای خطر صرفاً ضریب بتای توانیافته هستند (مثلاً نسبت خطر 1.047 برای Age معادل exp (0.04589) است که در این مدل 0.04589 ضریب بتای Age است.
با در نظر گرفتن همه این موارد، میتوان دریافت که نتیجهگیری کلی از این مدل تاکنون این است که انتظار داریم افراد مسنتر با عملکرد قلب ضعیف (low ejection fraction)، فشار خون بالا و عملکرد ضعیف کلیه (high serum creatinine)، پیشبینی میشود که نرخ خطر بالاتر (و در نتیجه زمان بقا کمتر) داشته باشند.
همچنین توجه داشته باشید که اگرچه نسبت خطر برای سن نسبتاً کوچک به نظر میرسد (1.047 برای سن در مقایسه با 2.226 برای کراتینین سرم بالا، به عنوان مثال)، این اثر سن در سال است. این بدان معناست که نرخ خطر برای یک سال افزایش سن فقط با ضریب ${{1.047}^{1}}=1.047$ افزایش مییابد، اما برای افزایش سنی ده ساله، ضریب خطر ${{1.047}^{{10}}}=1.58$ افزایش مییابد!
در جدول بالا میتوانید علاوه بر براورد عددی نسبت خطر، فاصله اطمینان 95 درصد براورد شده برای Hazard Ratio را نیز مشاهده کنید.
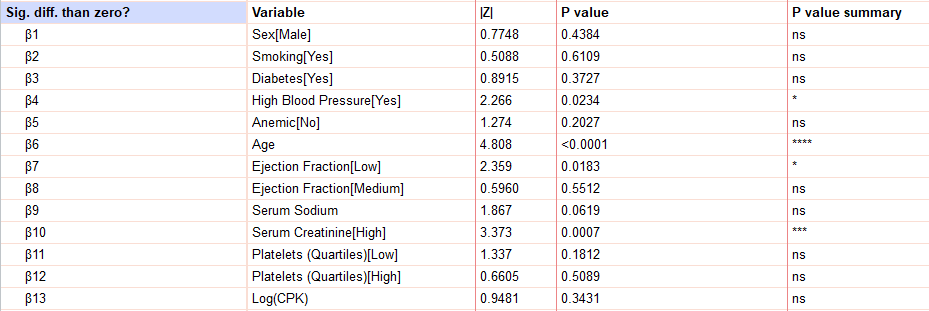
- Sig. diff. than zero?
در هر آزمون آماری از جمله انواع رگرسیونها، این مطلب مهم است که دریابیم آیا تاثیر کمیت مستقل ما بر روی کمیت وابسته معنادار بوده است یا خیر؟ پاسخ به این سوال را میتوانیم با استفاده از مقدار احتمال P value بدهیم. در تصویر زیر بخش مربوط به نتایج معناداری X های مدل رگرسیون کاکس، آمده است.
بر مبنای نتایج بالا میتوانیم دریابیم که فشار خون بالا، سن، Ejection Fraction[Low] و کراتینین سرم [بالا] بر بقا افراد مورد مطالعه، تاثیر معنادار دارد. این یافته در سطح معنیداری 0.05 به دست میآید.
- Model diagnostics
بخش بعدی نتایج در رگرسیون خطرات متناسب کاکس، یافتههایی را ارایه میکند که مدل مشخصشده را با مدلی که فاقد کمیتهای پیشبینیکننده است، مقایسه میکند. به طور پیش فرض، مقادیر نمایش داده شده در اینجا شامل تعداد پارامترهای هر یک از مدلها و مقدار معیار اطلاعات Akaike’s Information Criterion (AIC) است.

اعداد AIC بیان شده در این بخش به شما امکان میدهد تا به سرعت ارزیابی کنید که آیا مدل مشخص شده در تحلیل عملکرد بهتری نسبت به مدل خالی (فاقد Xها) در برازش دادهها دارد یا خیر. روش محاسبه مقادیر AIC کمی پیچیده است، اما استفاده از این مقادیر برای مقایسه دو مدل در واقع ساده است، به این ترتیب که AIC کوچکتر نشاندهنده تناسب بهتر مدل است. با در نظر گرفتن مقادیر 970.9 برای مدل بدون Xها و 913.1 برای مدل مشخص شده، میتوانیم تعیین کنیم که مدل مشخصشده کار بهتری برای توصیف دادههای مشاهده انجام میدهد.
- Hypothesis tests
به خاطر داشته باشید به هنگام بیان تنظیمات رگرسیون کاکس در نرمافزار Prism و در تب Goodness of fit از معیارهایی که نرمافزار جهت بررسی مناسب بودن مدل رگرسیونی استفاده میکند، نام بردیم. در جدول زیر نتایج مربوط به این آزمونها به دست آمده است.

مقدار احتمال P value به دست آمده از این آزمونهای نیکویی برازش، بیانگر مناسب بودن و معنادار بودن مدل رگرسیون خطرات متناسب کاکس برازش شده بر دادهةای مطالعه است.
- Concordance probability
از دیگر یافتههای نرمافزار که آن را هم میتوانیم مربوط به آمارههای نیکویی برازش دانست، آماره C هارل Harrell’s C است. قبلاً درباره این آماره در تنظیمات Prism و در تب Goodness of fit صحبت کردیم. در جدول زیر میتوانید نتایج این یافته را ببینید.

عدد Harrell’s C-statistic برابر با 0.742 به دست آمده است. این عدد نشاندهنده این است که مدل به درستی حدود 74 درصد از جفتهای مشاهده را پیشبینی میکند.
- Data summary
آخرین بخش در صفحه نتایج رگرسیون مخاطرات متناسب Cox خلاصهای از دادههای مطالعه را ارایه میکند. مانند تعداد افراد موجود در مطالعه، تعداد افرادی که نادیده گرفته شدهاند، تعداد پیوندها (مشاهدات با رویدادهایی که دارای زمان سپری شده یکسان هستند).
همچنین تعداد مشاهدات سانسور شده و تعداد مشاهدات با مرگ/رویداد مورد علاقه و نسبت مشاهدات سانسور شده به رویدادها گزارش میشود. بسته به رویداد مورد مطالعه، این نسبت ممکن است به طور قابل توجهی متفاوت باشد (زمانی که رویداد نسبتاً غیر معمول است، نسبت مشاهدات سانسور شده به رویدادها ممکن است مانند این مثال بزرگ باشد؛ زمانی که رویداد رایج است، نسبت ممکن است بسیار کوچک باشد، زیرا اکثر موارد مشاهدات منجر به وقوع رویداد خواهد شد).
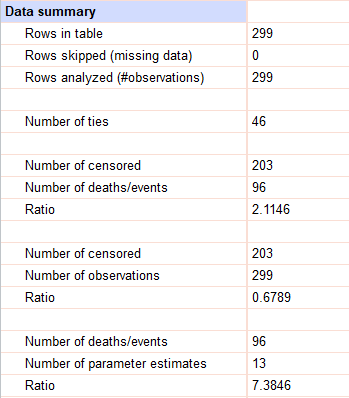
علاوه بر این در این بخش، تعداد مشاهدات سانسور شده و تعداد کل مشاهدات به همراه نسبت این دو مقدار (کسری از مشاهدات مورد استفاده در تحلیل که سانسور شدهاند) بیان میشود. در نهایت، تعداد مشاهدات با مرگ/رویداد مورد علاقه ثبت شده همراه با تعداد کل تخمینهای پارامتر و نسبت این دو مقدار گزارش میشود. معمولاً این نسبت باید حدود ده باشد.
برگه دیگر نتایج رگرسیون کاکس با نام Individual values دیده میشود. در جدول زیر میتوانید بخشی از نتایج این برگه را ببینید.
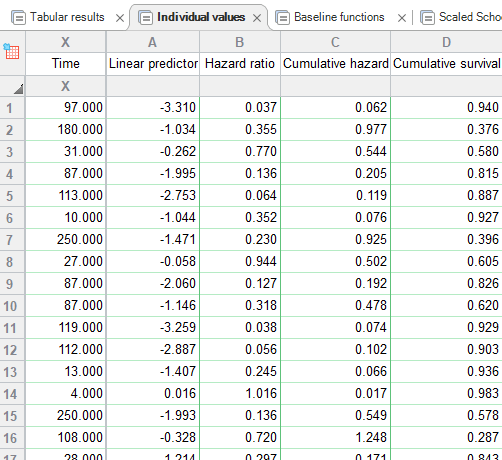
هنگامی که مدل کاکس تعریف شد، یافتههای بیشتری را میتوان برای هر یک از مشاهدات و افراد موجود در مطالعه، ارایه کرد. این نتایج علاوه بر ستون Time که بیانگر مدت بقا برای هر فرد میباشد، شامل یافتههای زیر است.
- Linear predictor, XB
به آن پیشبینی خطی گفته میشود و مقداری است که برای عبارت $ \displaystyle \sum\limits_{i}{{{{x}_{i}}}}{{\beta }_{i}}$ در مدل ریاضی کاکس به دست میآید. پس از وارد کردن پارامترهای برآورد شده $ \displaystyle \left( {{{\beta }_{i}}} \right)$ و همچنین مقادیر عددی هر یک از کمیتهای پیشبینی $ \displaystyle {\left( {{{x}_{i}}} \right)}$، به ازای هر فرد محاسبه میشود. مقدار به دست آمده در این ستون نشان میدهد برای هر فرد نرخ خطر چقدر از خطر پایه، متفاوت است.
- Hazard ratio, exp(XB)
به آن نسبت خطر گفته میشود و پیشبینی خطی توانی (XB) است. این مقدار برای تعیین میزان خطر از نرخ خطر پایه، یا بقا تجمعی از بقا تجمعی پایه استفاده میشود. رگرسیون کاکس به شدت بر فرض خطرات متناسب تکیه دارد (که نرخ خطر برای هر فرد متناسب با برخی از خطرات پایه ناشناخته است). در این ستون، HR ریسک نسبی تناسب را به ازای هر فرد نشان میدهد و به معنای این است که خطر یک فرد خاص چند بار بیشتر یا کمتر از خطر پایه است.
- Cumulative hazard H(t)
خطر تجمعی H(t) نامیده میشود و توسط مدل برای فرد در زمان سپری شده معین مشاهده (کل خطر انباشته تا زمان t) برآورد شده است. مقادیر بالاتر خطر تجمعی با مقادیر کمتر احتمال بقا مطابقت دارد. این مقدار برای تعدادی از موارد ریاضی/محاسباتی مهم است و به همین دلیل در جدول نتایج قرار گرفته است. با این حال به راحتی قابل تفسیر مستقیم نیست. رابطه بین خطر تجمعی و بقا تجمعی را میتوان با استفاده از فرمول زیر مشاهده کرد.
$ \displaystyle H\left( t \right)=-\ln S\left( t \right)$
- Cumulative survival S(t)
بقا تجمعی S(t) گفته میشود و بقا فرد برآورد شده توسط مدل کاکس، با توجه به زمان سپری شده است. این عدد مقدار احتمال زنده ماندن یک فرد تا زمان t را نشان میدهد. این مقدار از تابع بقای پایه (به برگه نتایج Baseline functions مراجعه کنید) و با استفاده از فرمول زیر محاسبه میشود.
$ \displaystyle S\left( t \right)={{S}_{0}}{{\left( t \right)}^{{\exp \left\{ {\sum\limits_{i}{{{{x}_{i}}}}{{\beta }_{i}}} \right\}}}}$
توجه داشته باشید، با استفاده از دو معادله ارایه شده در بالا، مقدار براورد شده توسط مدل برای خطر تجمعی هر فرد را میتوان مستقیماً از تابع بقای پایه و مقدار پیشبینی خطی (XB) محاسبه کرد. روابط زیر را ببینید.
$ \displaystyle \begin{array}{l}H\left( t \right)=-\ln S\left( t \right)\\\to \\H\left( t \right)=-\ln \left( {{{S}_{0}}{{{\left( t \right)}}^{{\exp \left\{ {\sum\limits_{i}{{{{x}_{i}}}}{{\beta }_{i}}} \right\}}}}} \right)\\\to \\H\left( t \right)=-\exp \left\{ {\sum\limits_{i}{{{{x}_{i}}}}{{\beta }_{i}}} \right\}\times \ln \left( {{{S}_{0}}\left( t \right)} \right)\end{array}$
یک هدف مهم هنگام انجام رگرسیون خطرات متناسب کاکس، پیشبینی احتمال بقا برای یک فرد معین در جمعیت مورد بررسی است. برای انجام این کار، منحنی بقا تجمعی پایه baseline cumulative survival curve و منحنی خطر تجمعی پایه baseline cumulative hazard curve براورد میشوند. فرآیند براورد این منحنیها از نظر ریاضی پیچیده است، با این حال میتوان به روش زیر در مورد آن فکر کرد.
- بقای تجمعی پایه، بقای تجمعی براورد شده است که کمیتهای پیشبینی کننده همه مقادیر صفر دارند.
- خطر تجمعی پایه به طور مشابه خطر تجمعی براورد شده است که کمیتهای پیشبینی کننده همه مقادیر صفر دارند.
برای محاسبه این مقادیر، Prism باید ابتدا کمیتی به نام آلفا (α) را محاسبه کند. توضیح کامل ریاضی آلفا از حوصله این مقاله خارج است. با این حال، مفهوم کلی آن به شرح زیر است.
- مشاهدات را با افزایش مقادیر زمان سپری شده تا رویداد مرتب کنید. این مفهوم به معنای آن است که افراد را به ترتیب از Time کم به زیاد مرتب کنید.
- برای هر Time، مقادیر ریسک نسبی یعنی Exp(XB) را به دست بیاورید. این کار را برای افرادی که رویداد مورد علاقه را تجربه میکنند و همچنین افرادی که هنوز "در معرض خطر" در نظر گرفته میشوند (افرادی که رویداد مورد علاقه را تجربه نکردهاند یا تا این لحظه سانسور شدهاند)، انجام دهید.
- محاسبه آلفا با استفاده از نسبت مقادیر برای کسانی که رویداد مورد علاقه را تجربه کردهاند و کسانی که در معرض خطر هستند، انجام میشود.
- توجه داشته باشید که آلفا برای مشاهدات سانسور شده برابر با یک است.
در تصویر زیر میتوانید بخشی از نتایج برگه Baseline functions را ببینید. در ستون اول، اعداد آلفا به ازای هر Time آمده است.
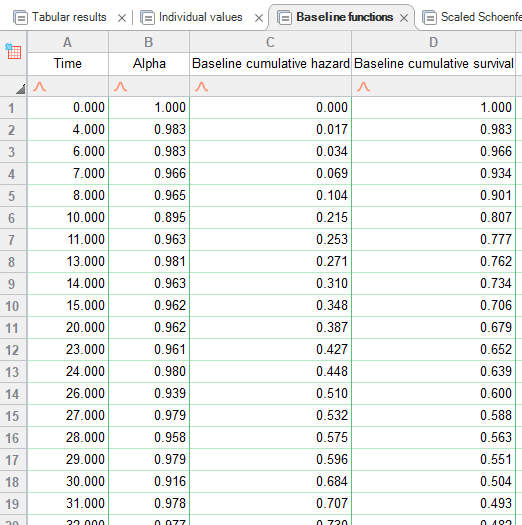
هنگامی که آلفا برای هر نقطه زمانی محاسبه شد، محاسبه بقای تجمعی پایه و مقادیر خطر تجمعی پایه ساده است و از نظر ریاضی پیچیده نیست. رابطه زیر را ببینید.
$\displaystyle {{S}_{0}}\left( t \right)=\Pi {{\alpha }_{t}}$
یعنی، بقای تجمعی پایه در زمان t برابر است با حاصلضرب تمام مقادیر آلفا تا (و از جمله) زمان t. برای تایید این نتایج در Prism، یک ردیف در ستون بقا تجمعی پایه Baseline cumulative survival انتخاب کنید. مقدار آلفای این سطر را با مقادیر آلفای تمام سطرهای قبل از این سطر، ضرب کنید. نتیجه به دست آمده همان مقدار بقای تجمعی پایه برای آن سطر خواهد بود.
مقادیر خطر تجمعی پایه یعنی ستون Baseline cumulative hazard از نظر محاسبه سادهتر است و میتوان آنها با استفاده از معادله زیر تعیین کرد.
$\displaystyle H\left( t \right)=-\ln S\left( t \right)$
پس از محاسبه بقای تجمعی پایه و خطر تجمعی پایه به ازای هر Time، نرمافزار نموداری را طراحی میکند که در آن میتوان این منحنیها را بررسی کرد. در بخش Graphs، میتوانید نمودار با نام Baseline functions را مشاهده کنید. در تصویر زیر آن را میبینید.
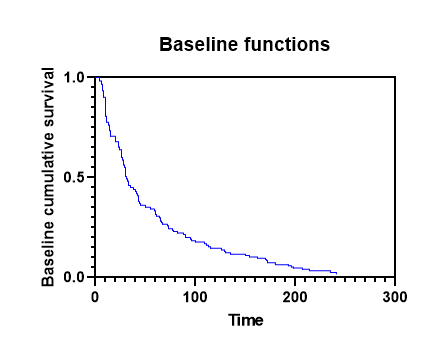
بهطور پیشفرض، بقای تجمعی Baseline روی محور Y رسم میشود، اما با دوبار کلیک کردن روی نمودار به شما امکان میدهد به گفتگوی Format Graph دسترسی داشته باشید و محور Y را روی نمایش خطر تجمعی پایه، قرار دهید.
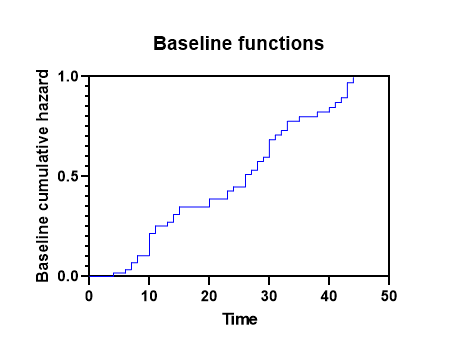
در ادامه نتایج نرم افزار Prism هنگامی که به ارایه تحلیل رگرسیون خطرات متناسب کاکس میپردازد، گرافها و خروجیهایی از باقیماندهها Residuals مدل رگرسیونی میباشد. من در یک مقاله جداگانه (باقیمانده ها Residuals در رگرسیون خطرات متناسب کاکس) به بیان این موضوع و گرافهای به دست آمده، پرداختهام. علاقمند بودید آن را ببینید.
آخرین نتایج و نمودارهای تولید شده توسط رگرسیون کاکس، منحنیهای بقا براورد شده برای گروههایی است که در برگه Graphs تنظیمات نرمافزار، آنها را مشخص کردهایم. من در این زمینه یک مقاله جداگانه نوشتهام. لینک (تنظیمات رسم نمودار ها Graphs در رگرسیون خطرات متناسب کاکس) آن را میتوانید مشاهده کنید.
به طور شهودی، به نظر میرسد که این نتایج با درک کلی از عوامل خطر مرتبط با نارسایی قلبی مطابقت دارد. به عبارت دیگر، بیماران مسن با عملکرد ضعیف قلب و کلیه و افزایش فشار خون، در معرض خطر بالاتر نارسایی قلبی نسبت به افراد جوانتر، با عملکرد بهتر قلب یا کلیه و فشار خون پایینتر، قرار دارند.
نمودارهای باقیمانده تولید شده توسط این آنالیز نشان میدهد که مفروضاتی که رگرسیون خطرات متناسب کاکس بر آنها تکیه دارد نقض نشده است. فقدان وجود روند در باقیماندههای Schoenfeld نشان میدهد که پیشفرض خطرات متناسب در این دادهها برقرار است. گراف باقیماندههای deviance در برابر Xهای مطالعه، نشان میدهد که هیچ نقطه پرت آشکاری در دادههایی که باید حذف شوند وجود ندارد.
یک روند ضعیف در نمودار باقیمانده deviance در برابر پیشبینی خطی/HR وجود داشت، با این حال این موضوع احتمالاً به دلیل تعداد زیاد دادههای سانسور شده در نمونه بود (نسبت مشاهدات سانسور شده به رویدادها = 2.1146 و نسبت مشاهدات سانسور شده به کل مشاهدات = 0.6789). این مطلب نشاندهنده نقض مفروضات خطی بودن مدل نیست.
جالب توجه است که تعدادی از کمیتهای پیشبینیکننده نتوانستند به مفهوم معناداری دست یابند (آنهایی که دارای مقادیر احتمال کمتر از 0.05 و یا فواصل اطمینان نسبتهای خطرشان شامل عدد 1 بود) از جمله جنسیت، وضعیت سیگار کشیدن و دیابت. نویسندگانی که دادههای این مثال از آنها بهدست آمد بیان میکنند که ممکن است به این دلیل باشد که این عوامل اغلب پیشبینیکننده مراحل اولیه نارسایی قلبی در نظر گرفته میشوند، در حالی که افراد در این مطالعه جمعیتی را نشان میدهند که مراحل پیشرفته نارسایی قلبی را نشان میدهند.
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2023). Results and outputs of Cox proportional hazards regression analysis. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/Cox-proportional-hazards-regression-results/.php
For example, if you viewed this guide on 12th January 2023, you would use the following reference
GraphPad Statistics (2023). Results and outputs of Cox proportional hazards regression analysis. Statistical tutorials and software guides. Retrieved January, 12, 2023, from https://graphpad.ir/Cox-proportional-hazards-regression-results/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.