آنالیز تشخیصی (Discriminate Analysis) در نرمافزار SPSS
آنالیز تشخیصی که آن را تحلیل ممیزی نیز میگویند، همانند رگرسیون خطی چندگانه است، با این تفاوت که کمیت وابسته نه تنها توزیع نرمال ندارد، بلکه یک کمیت رتبهای و یا اسمی با تعداد گروههای محدود است.
همانگونه که میدانیم در حالت خاصی که کمیت پاسخ دو مقداری باشد، از رگرسیون لجستیک استفاده میکنیم. اما اگر کمیت وابسته بیش از دو مقدار رستهای را بگیرد، باید از تحلیل تشخیصی استفاده کنیم. در این آموزش به چگونگی انجام آنالیز تشخیصی با استفاده از نرمافزار SPSS میپردازیم.
معادله آماری آنالیز تشخیصی
اگر X2 ،X1، … و Xp کمیتهای پیشگو و مستقل و Y کمیت وابسته و از نوع رستهای باشند، هدف از آنالیز تشخیصی، یافتن تابع خطی مانند
Y= β0 + β1X1 + β2X2 +…+ βpXp
است، به طوری که احتمال
P (Y=y | (X1,X2,…,Xp ) = (x1,x2,…,xp))
ماکزیمم شود. در حالتی که کمیت وابسته دارای g تا مقدار مختلف باشد، یعنی تعداد g رده را به خود بگیرد، هدف آن است که مشاهدات جدید مربوط به کمیتهای X2 ،X1، … و Xp را براساس یک تابع تشخیصی، به یکی از g گروه نسبت دهیم.
برای فهم بهتر مطلب به مثال زیر توجه کنید.
مثال آموزشی آنالیز تشخیصی در دادهها
در یک بررسی تعداد 1315 دانشآموز انتخاب شده و مطالعهای بر روی علائق آنها انجام گرفت. به هر دانشآموز، پرسشنامهای داده شد تا به سوالات آن پاسخ دهند. هر سوال درباره میزان علاقه دانشآموز به یکی از فعالیتهای غیردرسی است.
کمیتها عبارتند از جنسیت (X1)، ساختن کیت (X2)، مدلسازی کیت (X3)، طراحی (X4)، نقاشی (X5)، کار بیرون از منزل (X6)، محاسبه (X7)، توانایی در به تصویر کشیدن مدل (X8) و کیفیت مدرسه (X9).
رشته تحصیلی دانشآموزان (y) پس از قبولی آنها در دانشگاه مورد سوال قرار گرفت. رشتهها عبارت بودند از هنر (1)، روانشناسی (2) و مهندسی (3).
فایل داده این مثال آموزشی را میتوانید از اینجا Discriminate Analysis SPSS دریافت کنید.
تنظیمات و گزینههای آنالیز تشخیصی
میخواهیم با استفاده از مشاهدات به دست آمده، آنالیز تشخیصی را انجام داده و تعیین کنیم هر دانشآموز، با توجه به علاقمندی که دارد، در آینده در چه رشتهای تحصیل خواهد کرد. رشته تحصیلی دانشآموز کمیت وابسته است و علاقمندی به هر یک از فعالیتهای غیردرسی، یک کمیت پیشگو است.
ابتدا از مسیر زیر در نرمافزار SPSS استفاده میکنیم.
Analyze → Classify → Discriminant
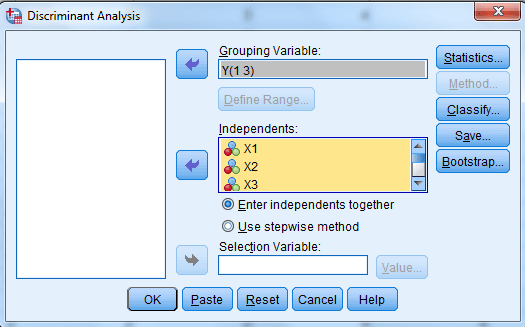
در پنجره باز شده کمیت y را انتخاب و در کادر لیست Grouping Variables قرار دهید.
روی دکمه Define Range کلیک کنید. در کادر Minimum عدد 1 و در کادر Maximum عدد 3 را وارد کنید. به خاطر دارید که کمیت (y) وابسته یعنی رشته تحصیلی دانشآموز در آینده را در سه گروه هنر، روانشناسی و مهندسی تعریف کردیم. سپس دکمه Continue را بزنید.
حال کمیتهای مستقل X2 ،X1، … و X9 را به کادر لیست Independents منتقل کنید.
دکمه Method در تنظیمات آنالیز تشخیصی
وارد کردن کمیتهای مستقل به معادله آنالیز تشخیصی، به دو صورت انجام میشود.
انتخاب گزینه Enter independents together سبب میشود که تمام Variableهای مستقل وارد مدل شوند.
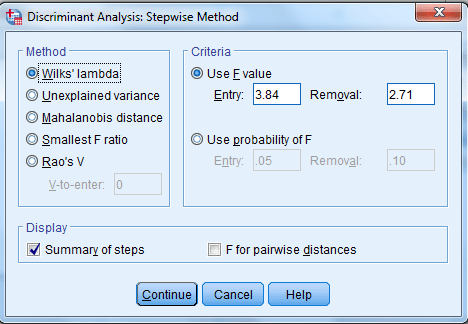
انتخاب گزینه Use stepwise methods سبب میشود که کمیتهای مستقل رگرسیونی برحسب درجه اهمیتی که در تعیین مقدار کمیت وابسته y دارند، گام به گام وارد معادله شوند. در هر مرحله اگر حضور یکی از کمیتها در معادله ضروری نباشد، آن کمیت از معادله خارج میشود. با انتخاب این گزینه، دکمه Method فعال میشود. با کلیک روی این دکمه، پنجره زیر باز میشود.
در بخش Method، روشهای مختلف انجام آنالیز تشخیصی، آمده است. به طور پیشفرض نرمافزار SPSS از روش Wilks’lambda استفاده میکند.
در بخش Criteria دو گزینه وجود دارد. گزینه Use F value وقتی استفاده میشود که بخواهیم ورود کمیتها به معادله یا خروج از معادله بر مبنای مقدار توزیع F باشد. گزینه Use probability of F نیز زمانی انتخاب میشود که ورود و خروج کمیتها بر مبنای احتمال توزیع F باشد.
دکمه Save در تنظیمات آنالیز تشخیصی
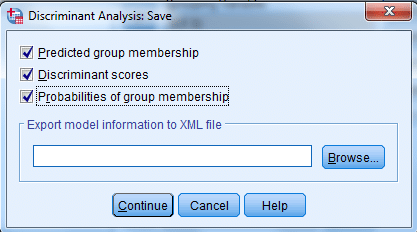
روی دکمه Save کلیک کنید تا پنجره زیر باز شود. هر سه کادر علامت این پنجره را فعال کنید.
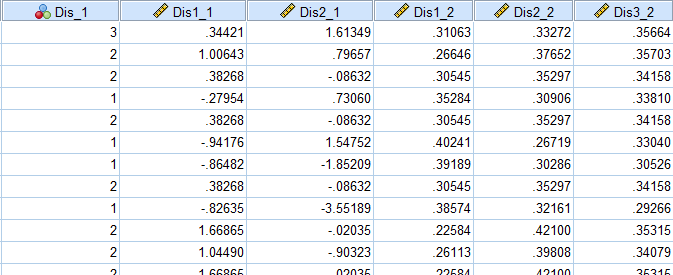
با انجام این کار، شش کمیت جدید با اسامی dis2_2 ،dis1_2 ،dis2_1 ،dis1_1 ،dis_1 و dis3_2 در فایل داده ساخته میشود.
کمیت dis_1 شماره یکی از سه گروه را نشان میدهد که هر سطر به آن گروه تعلق خواهد گرفت.
کمیتهای dis1_1 و dis2_1 امتیاز هر یک از افراد را براساس توابع تشخیصی نشان میدهند.
کمیتهای dis2_2 ،dis1_2 و dis3_2 به ترتیب، احتمال اختصاص هر فرد به یکی از سه گروه را نشان میدهد. توجه کنید که اگر مقدار dis1_2 بیشتر از dis2_2 و dis3_2 باشد، آنگاه این فرد به گروه 1 نسبت داده میشود و مقدار dis_1 آن برابر با 1 میشود.
دکمه Classify در تنظیمات آنالیز تشخیصی
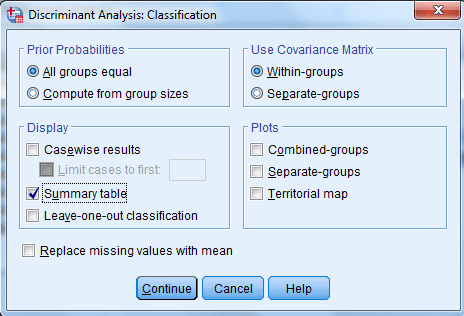
روی دکمه Classify کلیک کنید و در پنجره باز شده، در کادر Display گزینه summary table را فعال کنید.
انجام این کار سبب میشود جدولی با عنوان Classification Results در خروجی نتایج دیده شود.
دکمه Statistics در تنظیمات آنالیز تشخیصی
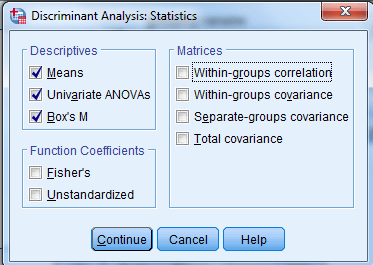
روی دکمه Statistics کلیک کنید. پنجره زیر باز میشود.
در کادر Descriptive انتخاب گزینه Means سبب میشود میانگین و انحراف معیار هر یک از کمیتهای مستقل، به تفکیک گروههای مختلف کمیت وابسته دیده شود.
فعال کردن گزینه Univariate ANOVAs آزمون برابری میانگین را برای هر یک از کمیتهای مستقل در گروههای Variable وابسته، انجام میدهد.
انتخاب گزینه Box’s M نیز آزمون برابری ماتریسهای کوواریانس را انجام میدهد.
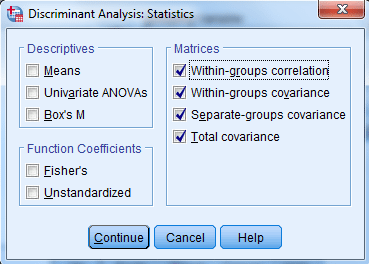
در این پنجره کادر دیگری نیز با عنوان Matrices وجود دارد.
انتخاب گزینهها سبب میشود، ماتریسهای همبستگی و کواریانس بین کمیتهای مستقل ایجاد شود.
حال روی دکمه OK کلیک کنید و نتایج آنالیز تشخیصی را ببینید. در ادامه به توضیح آنها پرداختهایم.
تحلیل نتایج به دست آمده از آنالیز تشخیصی
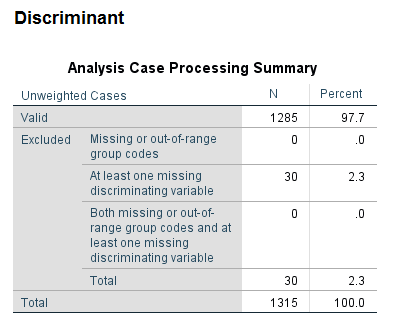
اولین جدولی که در خروجی نرمافزار دیده میشود جدول Analysis Case Processing Summary خواهد بود.
در این جدول تعداد دادههای Valid و Missing دیده میشود. نتایج نشان میدهد در 30 نفر از دانشآموزان (2.3 درصد از کل دانشآموزان مورد مطالعه) حداقل در یکی از کمیتهای نُهگانه مستقل داده گمشده وجود داشته است.
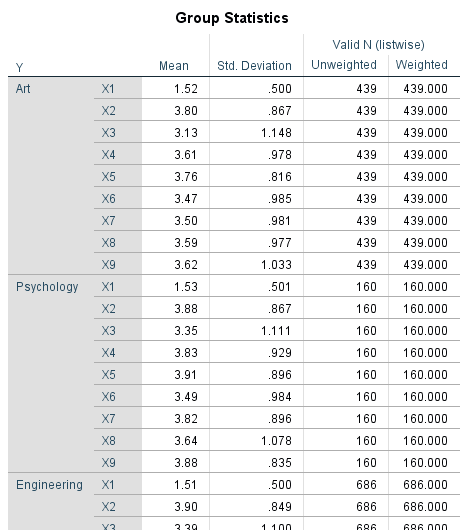
جدول بعدی Group Statistics حاصل انتخاب گزینه Means در کادر Descriptive از دکمه Statistics تنظیمات است.
همانگونه که مشاهده میشود، آمارههای میانگین، انحراف معیار و تعداد کمیتها براساس گروههای کمیت وابسته y آمده است.
در جدول Tests of Equality of Group Means نتایج آزمون همزمان برابری میانگین هر کمیت بین گروههای y دیده میشود.
بر مبنای نتایج که با آمارهی Wilks’ Lambda انجام شده است، کمیتهای مدلسازی کیت (X3)، طراحی (X4)، کار بیرون از منزل (X6)، محاسبه (X7) و کیفیت مدرسه (X9)، دارای مقادیر معنادار بین سه گروه رشتههای تحصیلی هنر، روانشناسی و مهندسی هستند.
به عبارت دیگر و به عنوان مثال مقادیر طراحی (X4) در گروههای تحصیلی از یکدیگر متفاوت است.
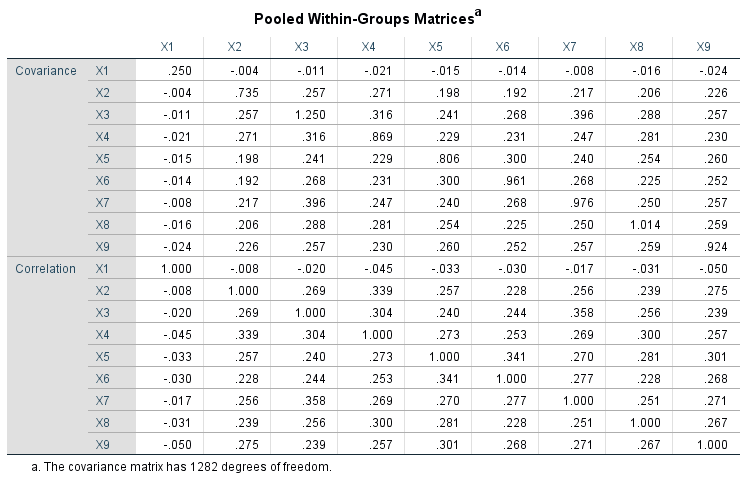
در جدول Pooled Within-Groups Matrices ماتریس کوواریانس و همبستگی بین کمیتهای مستقل مشاهده میشود.
در این ماتریس به خوبی نحوه و چگونگی ارتباط بین کمیتهای نُهتایی با یکدیگر دیده میشود.
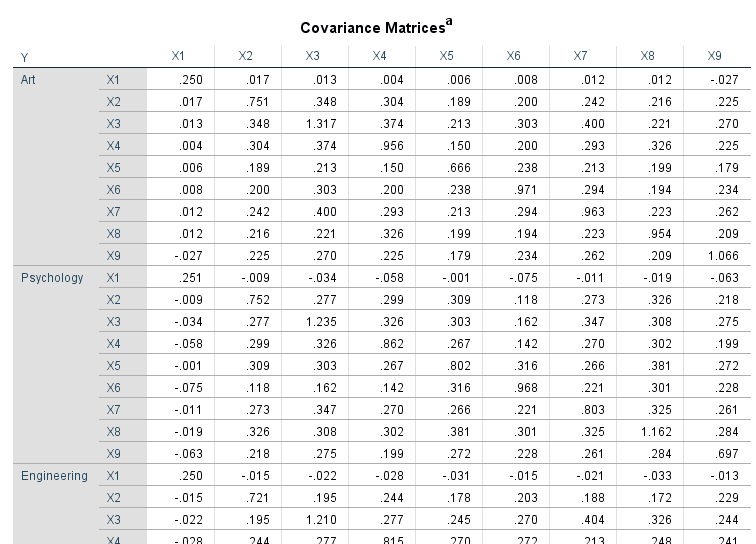
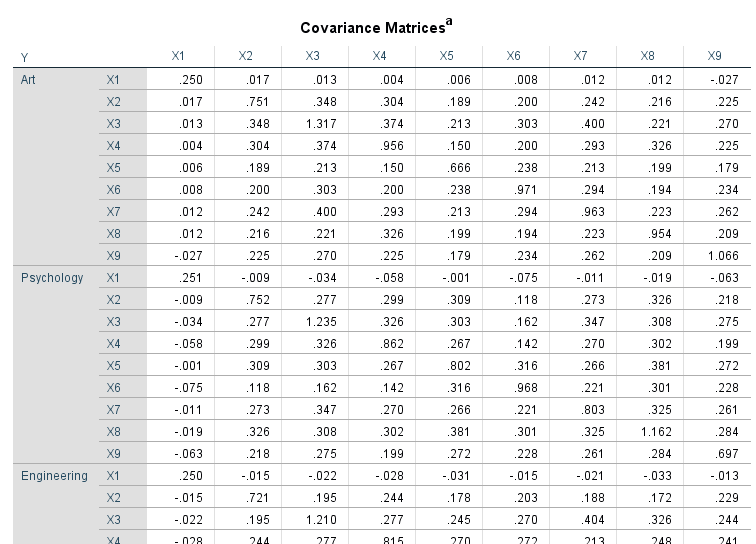
جدول بعدی نتایج با نام Covariance Matrices همان ماتریس کوواریانس است که اینبار به تفکیک گروههای سهگانه رشتههای تحصیلی، بیان شده است.
آزمون همگنی ماتریس کوواریانس در آنالیز تشخیصی
در ادامه نتایج آزمون برابری ماتریس کوواریانس سه گروه تحصیلی دیده میشود.
از آنجا که مقدار sig برابر با 0.067 به دست آمده است، فرض صفر یعنی همگنی ماتریسهای کوواریانس را میپذیریم.
توابع کانونی در آنالیز تشخیصی
در ادامه نتایج به دست آمده از آنالیز تشخیصی را در بخش Summary of Canonical Discriminant Functions بررسی میکنیم.
اولین جدول با نام Eigenvalues دیده میشود.
بر مبنای نتایج این جدول، دو تابع خطی آنالیز تشخیصی به دست آمده است، که به آنها توابع کانونی نیز گفته میشود. در این رابطه باید گفت که تعداد توابع برابر با تعداد کمیتهای مستقل است، اگر تعداد گروههای کمیت وابسته بیشتر از تعداد کمیتهای مستقل باشد. در غیر این صورت، تعداد توابع کانونی یکی کمتر از تعداد گروههای تشکیلدهنده کمیت y خواهد بود.
در این مثال 9 کمیت مستقل و 3 گروه تحصیلی در y داریم. بنابراین تعداد توابع کانونی 2=1-3 است.
مهمترین یافته در این جدول % of Variance است که نشان میدهد، هر تابع کانونی چه میزان از کمیتهای مستقل را تحت پیشبینی خود قرار دادهاند.
بر مبنای این یافته، مدل کانونی 1 توانایی تشخیص 74 و مدل کانونی 2 توانایی تشخیص 26 درصد را دارد.
در ستون Canonical Correlation نیز همبستگی کانونی در هر تابع کانونی بین کمیتهای مستقل با کمیت رشته تحصیلی آمده است.
در توضیح همبستگی کانونی باید عنوان کرد زمانی به کار میرود که بخواهیم ارتباط بین دو کمیت که خود دارای مولفههای مختلف هستند را به دست آوریم. در اینجا ما از یک طرف با Variableهای نُهگانه مستقل به عنوان یک مجموعه به هم پیوسته به نام discriminating variables روبه رو هستیم که دارای نُه مولفه است و از طرف دیگر با Variable گروه تحصیلی با سه گروه، مواجه هستیم.
ضریب همبستگی کانونی در اینجا ارتباط بین این دو کمیت (discriminating variables و y) را در هر تابع کانونی به دست میدهد.
جدول Wilks’ Lambda در آنالیز تشخیصی
جدول بعدی با عنوان Wilks’ Lambda دیده میشود.
در این جدول نتایج برای هر دو تابع کانونی و یا فقط تابع کانونی شماره 2 آمده است.
آماره Wilks’ Lambda یک آماره چندگانه محاسبه شده توسط SPSS است و به صورت (canonical 1-correlation2) محاسبه میشود.
مقدار احتمال به دست آمده نیز آزمون معناداری ضریب همبستگی کانونی را انجام میدهد.
بر مبنای نتایج ضریب همبستگی کانونی برای هر دو تابع کانونی، معنادار است.
طراحی مدل در آنالیز تشخیصی
حال به بررسی مدلها و توابع به دست آمده در تحلیل تشخیصی میپردازیم.
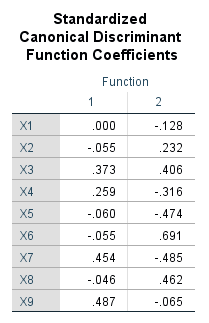
در جدول Standardized Canonical Discriminant Function Coefficients ضرایب استاندارد شده رگرسیونی برای هر کمیت در هر تابع کانونی آمده است.
بر مبنای نتایج به دست آمده مدل آنالیز تشخیصی به صورت زیر خواهد بود.
y (Function 1) = – 0.055 ZX2 + 0.373 ZX3 + 0.259 ZX4 – 0.060 ZX5 – 0.055 ZX6 + 0.454 ZX7 – 0.046 ZX8 + 0.487 ZX9
y (Function 2) = – 0.128 ZX1 + 0.232 ZX2 + 0.406 ZX3 – 0.316 ZX4 – 0.474 ZX5 + 0.691 ZX6 – 0.485 ZX7 + 0.462 ZX8 – 0.065 ZX9
در تابع 1 بیشترین مولفه تاثیرگذار X9 (کیفیت مدرسه) و در تابع 2 مولفه X6 (کار بیرون منزل) است.
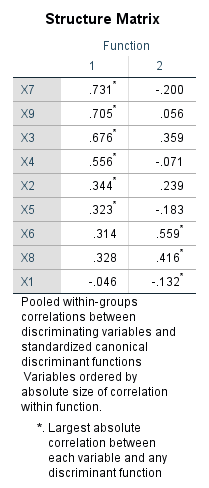
جدول بعدی به نام Structure Matrix نحوه قرار گرفتن هر کمیت در تابع کانونی را بیان میکند.
هر کمیتی که دارای بیشترین قدرمطلق عددی باشد در همان تابع قرار میگیرد. بر مبنای این نتایج X3 ،X9 ، X7 X5 ،X2 ،X4 به ترتیب اهمیت و بیشترین تاثیرگذاری مربوط به تابع کانونی شماره 1 و X1 ،X8 ،X6 به تابع کانونی شماره 2 تعلق دارند.
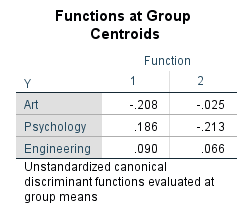
جدول بعدی با نام Functions at Group Centroids معرفی میشود.
میانگین مقادیر کمیت وابسته y به ازای هر گروه تحصیلی و در هر تابع کانونی به دست آمده است.
اندازههای به دست آمده در این جدول از روی روابط رگرسیونی جدول Standardized Canonical Discriminant Function Coefficients به دست میآید.
طبقهبندی نتایج در آنالیز تشخیصی (Classification Statistics)
در جدول Classification Processing Summary تعداد سطرهای مورد تحلیل و نادیده گرفته شده، مشخص میشود.
در این مثال از مجموع 1315 فرد، 1285 نفر مورد تحلیل تشخیصی قرار گرفتهاند. در 30 سطر نیز حداقل یک کمیت تشخیصی گمشده وجود داشته است که از تحلیلها کنار گذاشته شدهاند.
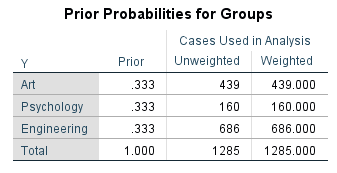
آنالیز تشخیصی از یک احتمال پیشین به عنوان نقطه شروع آنالیز استفاده میکند. مقدار این احتمال به نسبت گروههای کمیت وابسته y یکسان است. از آنجا که سه گروه y داریم، پس احتمال پیشین برابر با 0.333=1/3 میشود.
در جدول Prior Probabilities for Groups همچنین تعداد سطرهای مورد آنالیز به ازای هر گروه y مشخص شده است.
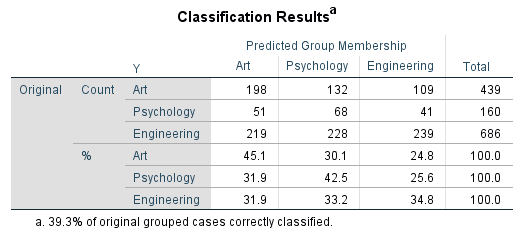
آخرین جدول آنالیز تشخیصی با نام Classification Results نامیده میشود.
این جدول در آنالیز تشخیصی بسیار مهم است و نشان میدهد، تحلیل به چه میزان درست کار کرده است. در ستون این جدول با نام Predicted Group Membership فراوانی و درصد قرار گرفته در هر رشته تحصیلی براساس مدل پیشبینی آنالیز تشخیصی قرار گرفته است.
در سطرهای جدول با نام Original فراوانی و درصد واقعی و مشاهده شده قرار دارد.
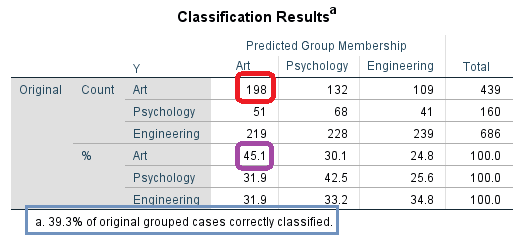
به عنوان مثال عدد198 نشان میدهد از مجموع 439 نفری که دارای رشته هنر بودهاند، مدل آنالیز تشخیصی ما 198 نفر را به درستی در این رشته پیشبینی کرده است. این میزان برابر با 45.1 درصد کل افراد دارای رشته تحصیلی هنر است. به همین ترتیب سایر اعداد جدول تفسیر میشود.
در نهایت مدل آنالیز تشخیصی توانسته است، رشته تحصیلی 39.3 درصد افراد را به درستی تشخیص دهد.
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2020). Discriminate Analysis with SPSS Software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/discriminate-analysis-with-spss/.php
For example, if you viewed this guide on 12th January 2022, you would use the following reference
GraphPad Statistics (2020). Discriminate Analysis with SPSS Software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/discriminate-analysis-with-spss/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.