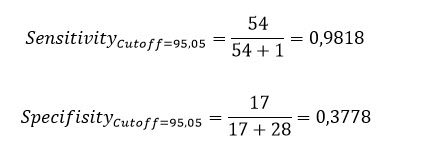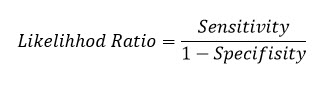منحنی ROC ، نقطه برش ، حساسیت و ویژگی
منحنی راک
ROC Curve
منحنی راک ROC Curve که از آن با نام منحنی مشخصه عملکرد سیستم Receiver Operating Characteristics نام برده میشود، از ابزارهای تشخیصی عملکرد یک سیستم و یا یک تست و روش درمانی، به حساب میآید. با استفاده از نتایج به دست آمده از منحنی ROC میتوان مفاهیمی مانند نقطه برش Cutoff ، حساسیت Sensitivity و ویژگی Specificity یک تست را به دست آوریم.
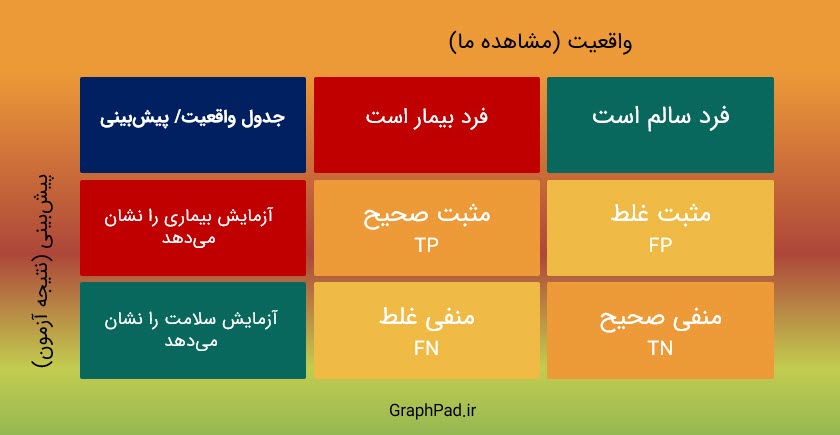
قبل از بیان این مثال در نرمافزار گراف پد، خوب است چند اصطلاح مهم مورد استفاده در این زمینه را تعریف کنیم. ابتدا جدول زیر را ببینید.
این جدول که نام آن را واقعیت / پیشبینی میگذاریم در ستونهای خود دو حالت فرد بیمار و یا فرد سالم باشد را نشان میدهد. در سطرها نیز میتوان نتیجه تست و آزمایش را که یکی بیماری را در فرد نشان میدهد و دیگری سلامت را در فرد نشان میدهد، مشاهده کرد.
- در حالت TP که نام آن مثبت صحیحی است وضعیتی را نشان میدهد که فرد واقعاً بیمار است و آزمایش نیز به درستی بیماری را نشان میدهد.
- به همین ترتیب TN یا منفی صحیح نیز حالتی است که فرد واقعاً سالم است و آزمایش نیز به درستی او را سالم نشان میدهد.
دو حالت اشتباه میتواند در اینجا رخ دهد.
- یکی FP یا مثبت غلط که فرد سالم است اما آزمایش به اشتباه بیماری را نشان میدهد و دیگری FN که فرد بیمار است اما آزمایش به اشتباه فرد را سالم نشان میدهد.
با این تعاریف، حال بیایید مفاهیم حساسیت Sensitivity و ویژگی Specificity را تعریف کنیم. اولین نکته اینکه هر دو این مفاهیم از جنس احتمال و در نتیجه عددی بین صفر و یک و یا بین صفر و 100 درصد هستند.
حساسیت به احتمال مثبت شدن صحیح نتیجه آزمایش وقتی که فرد بیمار است، اشاره میکند. یعنی میتوان آن را به صورت زیر به دست آورد. حساسیت را نرخ مثبت صحیح نیز مینامند.
ویژگی نیز به احتمال منفی شدن صحیح نتیجه آزمایش وقتی که فرد سالم است، اشاره میکند. ویژگی به صورت زیر به دست آورد. ویژگی را نرخ منفی صحیح نیز میگویند.
منحنی ROC دارای سه بخش است، در ادامه آنها را توضیح خواهیم داد.
- بالای خط نیمساز.
در این بخش نقاطی قرار گرفتهاند که مقدار حساسیت آنها نسبت به FPR بیشتر است. به معنای آنکه در این بخش، نرخ مثبت صحیح بیشتر از نرخ مثبت کاذب است. قرار گرفتن نقاط در این محیط مطلوب ما خواهد بود.
- روی خط نیمساز.
در این بخش مقدار عددی نرخ مثبت صحیح و نرخ مثبت کاذب با یکدیگر برابر است. به عبارتی از هر 100 نفر بیمار، آزمایش در 50 نمونه به درستی بیماری را تشخیص میدهد و در 50 نمونه نیز به غلط سلامت افراد را نشان میدهد. این نقاط چندان مطلوب ما نیستند.
- پایین خط نیمساز.
در این بخش نقاطی قرار گرفتهاند که مقدار حساسیت آنها نسبت به FPR کمتر است. یعنی در این بخش، نرخ مثبت صحیح کمتر از نرخ مثبت کاذب است. قرار گرفتن نقاط در این بخش اصلاً مطلوب ما نیست.
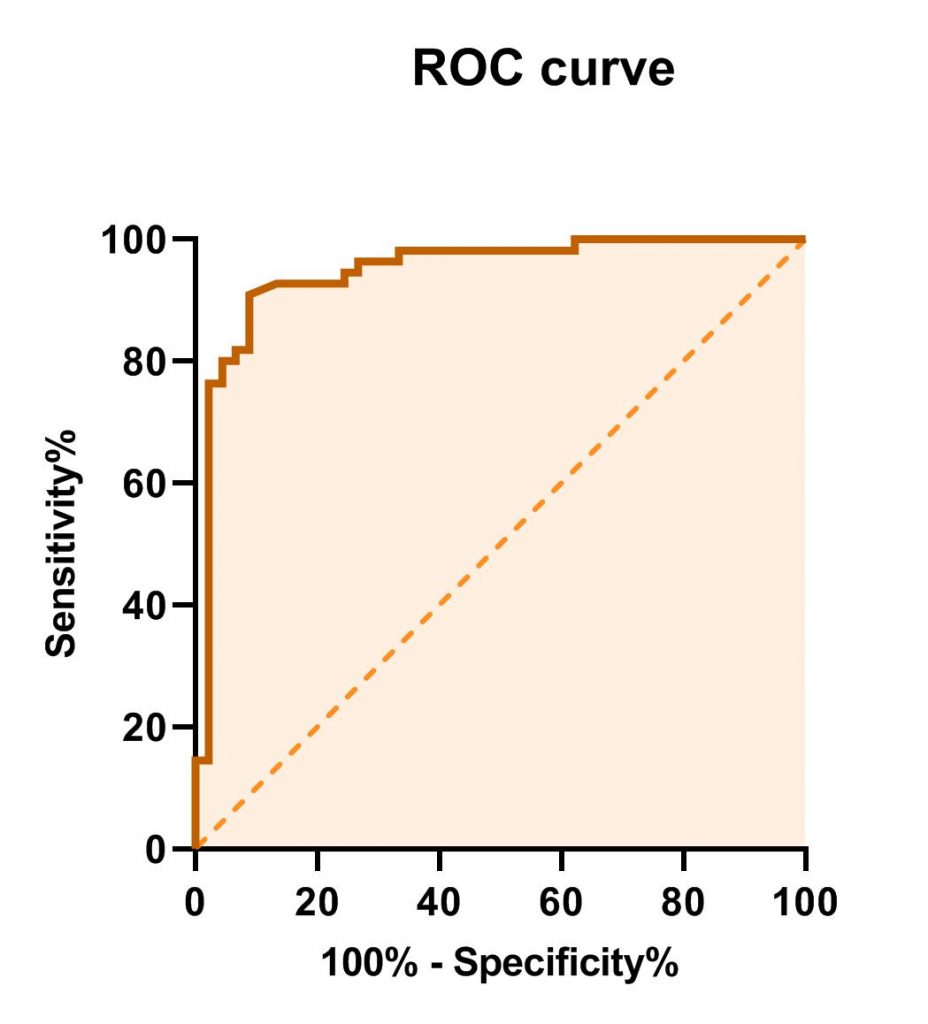
خوب است در همین جا و قبل از شروع بحث مثال گراف پد با مفهومی به نام سطح زیر منحنی راک Area under the ROC curve که معمولاً به اختصار AUC نامیده میشود، نیز آشنا شویم. در ابتدا شکل زیر را ببینید.
این شکل همان ROC Curve بالا است که سطح زیر منحنی آن مشخص شده است. ما به این سطح AUC میگوییم. مقدار عددی AUC به وضوح عددی بین صفر تا یک است و نشان میدهد قدرت تشخیص یک تست چقدر است. اگر این عدد به یک نزدیک باشد به معنای آن است که دادهها عموماً در بالای خط نیمساز قرار گرفتهاند و میزان نرخ مثبت صحیح بالا است. اعداد AUC نزدیک به 0.5 همان برابری نرخ مثبت صحیح و نرخ مثبت کاذب را نشان میدهد و اعداد کمتر از 0.5 بیانگر بالاتر بودن نرخ مثبت کاذب در مقایسه با نرخ مثبت صحیح است.
در زمینه اندازههای عددی AUC میتوان جدول زیر را مدنظر قرار داد.
| اندازه عددی AUC در منحنی راک | قدرت تشخیص تست |
| 0.9 تا 1 | عالی |
| 0.8 تا 0.9 | خوب |
| 0.7 تا 0.8 | نسبتاً خوب |
| 0.6 تا 0.7 | ضعیف |
| 0.5 تا 0.6 | بیفایده |
| کمتر از 0.5 | غیر قابل استناد |
حال با بیان این توضیحات ابتدایی، میخواهیم به مثال نرمافزار گراف پد در زمینه ROC Curve بپردازیم. در این مثال سعی میکنیم علاوه بر رسم منحنی راک به مفهومی به نام نقطه برش Cutoff نیز بپردازیم.
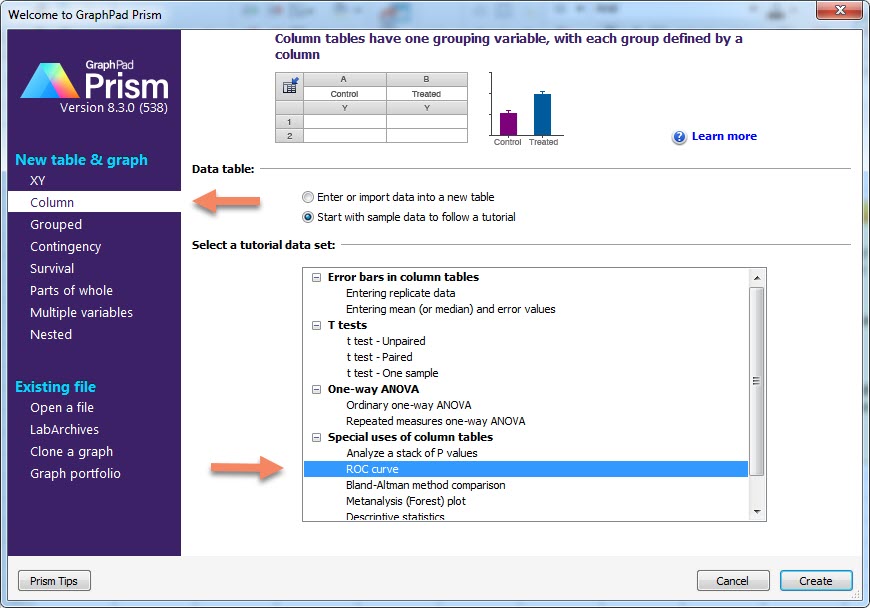
این مثال با نام ROC Curve در دسته تحلیلهای Column و در بخش Special uses of column tables صفحه ورودی نرمافزار گراف پد قرار دارد. فایل مثال را میتوانید از اینجا دانلود کنید.
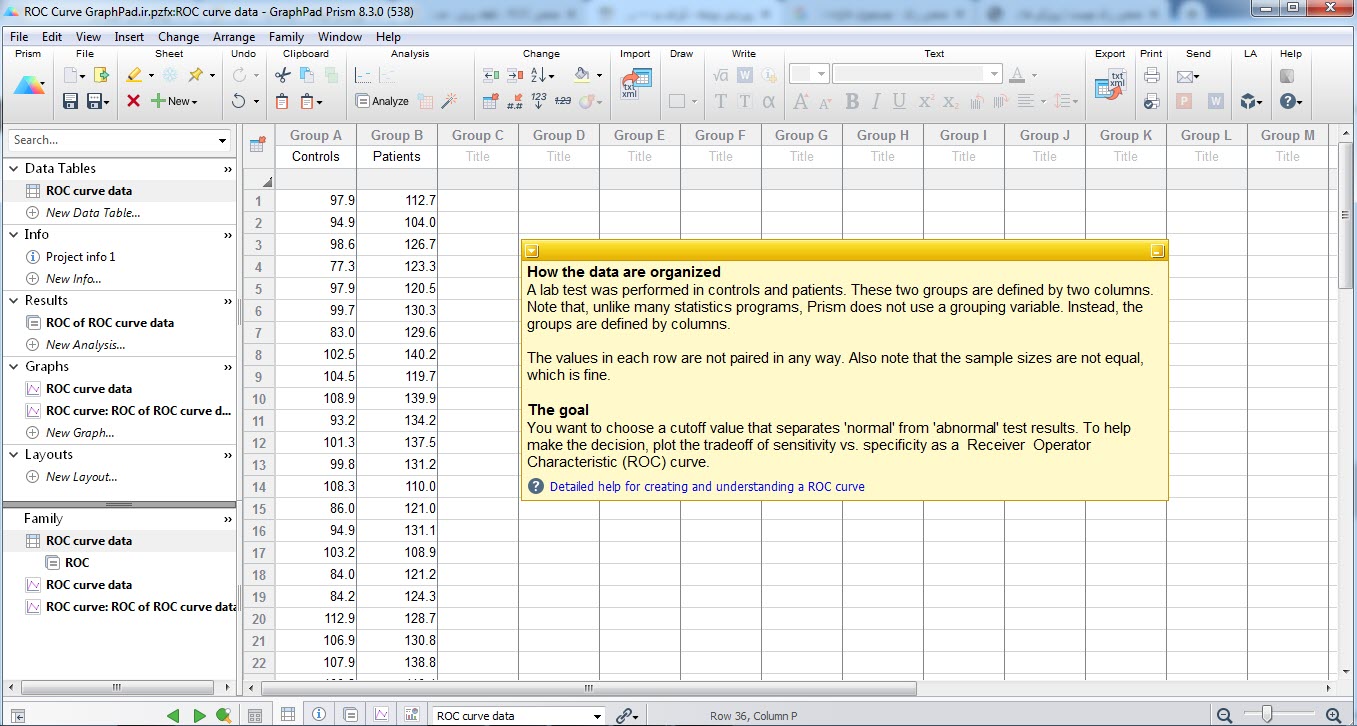
وقتی مثال را Create میکنیم با دادههای زیر روبهرو میشویم. همانگونه که مشاهده میکنید و در Note مثال نیز آمده است، دادهها در دو ستون Control و Patients که از یکدیگر مستقل هستند، بیان شده است. در گروه کنترل 45 نفر و در گروه بیماران 55 نفر آمده است. بنابراین همانگونه که گراف پد نیز به آن اشاره میکند در یک مطالعه ROC Curve لزومی ندارد تعداد افراد دو گروه با یکدیگر برابر باشند.
در این مثال میخواهیم یک نقطه برش که با استفاده از آن بتوانیم نتایج آزمایش را به دو گروه نرمال و غیرنرمال، جدا کنیم، به دست آوریم. برای این منظور منحنی ROC را نیز رسم خواهیم کرد. در این مثال و در ادامه با مفهومی با نام سطح زیر منحنی راک Area under the ROC curve که معمولاً به اختصار AUC نامیده میشود، آشنا خواهیم شد.
برخلاف بسیاری از مثالهای گراف پد که پس از مشاهده دادهها به سراغ بخش Graphs از پنجره سمت راست (Navigator Panel) میرفتیم و انواع نمودارهای قابل رسم با نرمافزار را مشاهده میکردیم، اینبار و در مثال ROC Curve ابتدا آنالیز آماری انجام داده و پس از آن به دنبال مشاهده گراف رسم شده و به دست آوردن نتایج در فولدر Results خواهیم بود.
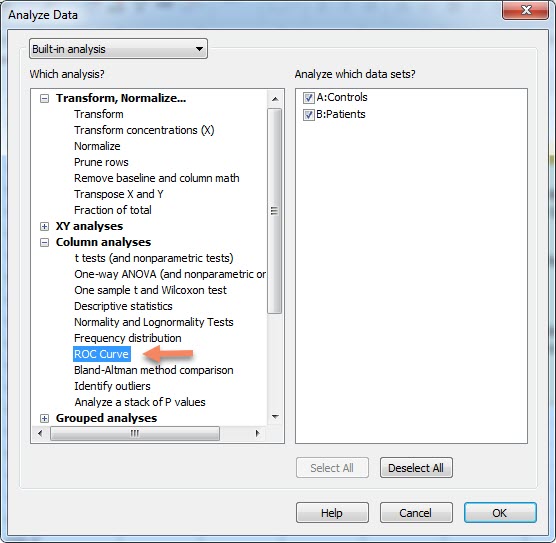
جهت انجام تحلیل در این مثال در شیت دادهها از منوی Analyze در بالای صفحه، گزینه ROC Curve را انتخاب میکنیم.
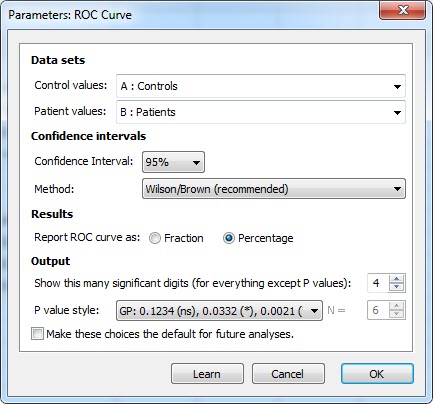
پنجره زیر با نام Parameters: ROC Curve برای ما باز میشود. در این پنجره به اختصار تنظیمات تحلیل منحنی راک آمده است.
- Data sets.
به سادگی مشخص میکنیم که ستون اندازههای کنترل و اندازههای بیمار برای ما کدام باشد. در این مثال چون دو ستون بیشتر نداریم، بنابراین Control values همان ستون Controls و Patients values همان ستون Patients خواهد بود.
- Confidence intervals.
فاصله اطمینان ما چند درصد باشد. به سادگی از کشو باز شده میتوان ضریب اطمینان دلخواه برای فاصله اطمینان را نیز مشخص کرد. گراف پد در این زمینه از روشی با نام Wilson/Brown استفاده میکند.
- Results.
نمایش منحنی راک به صورت درصدی Percentage باشد و یا کسری Fraction. به صورت پیش فرض نمایش درصدی جلوه بهتری دارد.
- Output.
اینجا با چیز خاصی روبهرو نیستیم و در اکثر پنجرههای تنظیمات گراف پد نیز میآید. این بخش درباره نحوه و تعداد نمایش مقادیر احتمال نتایج صحبت میکند.
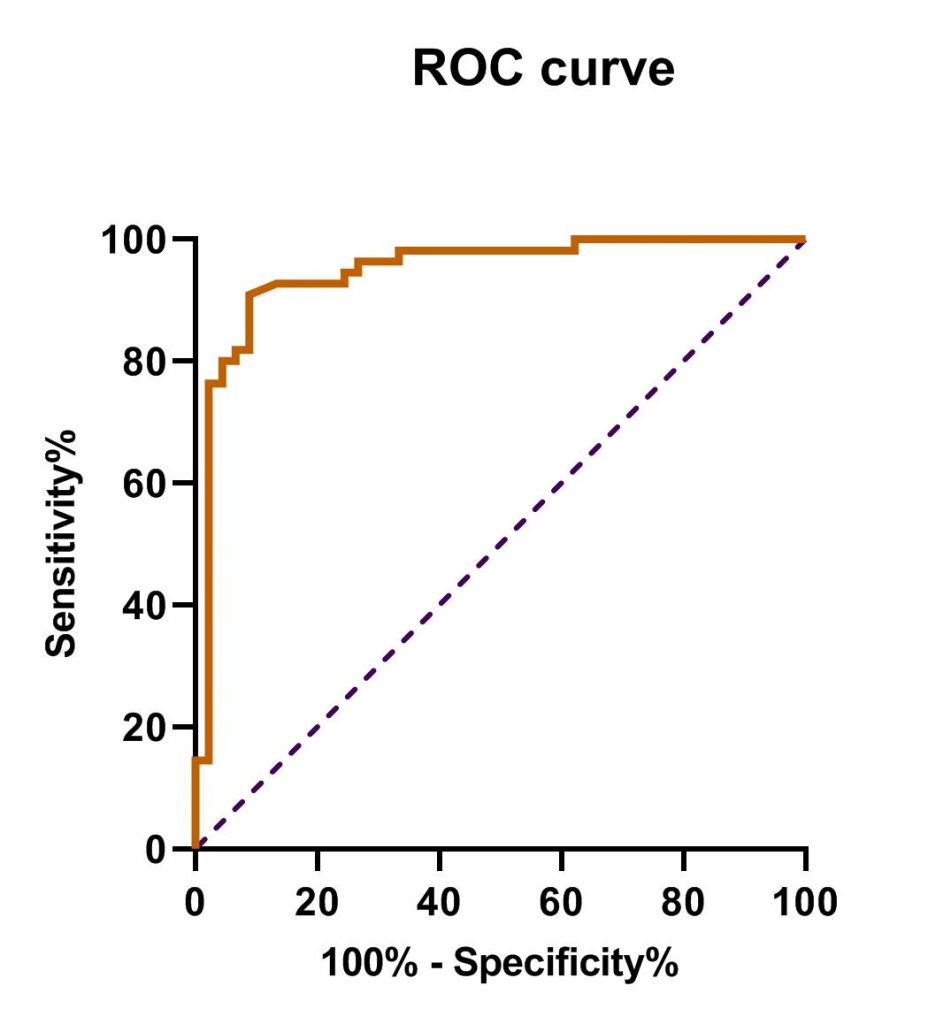
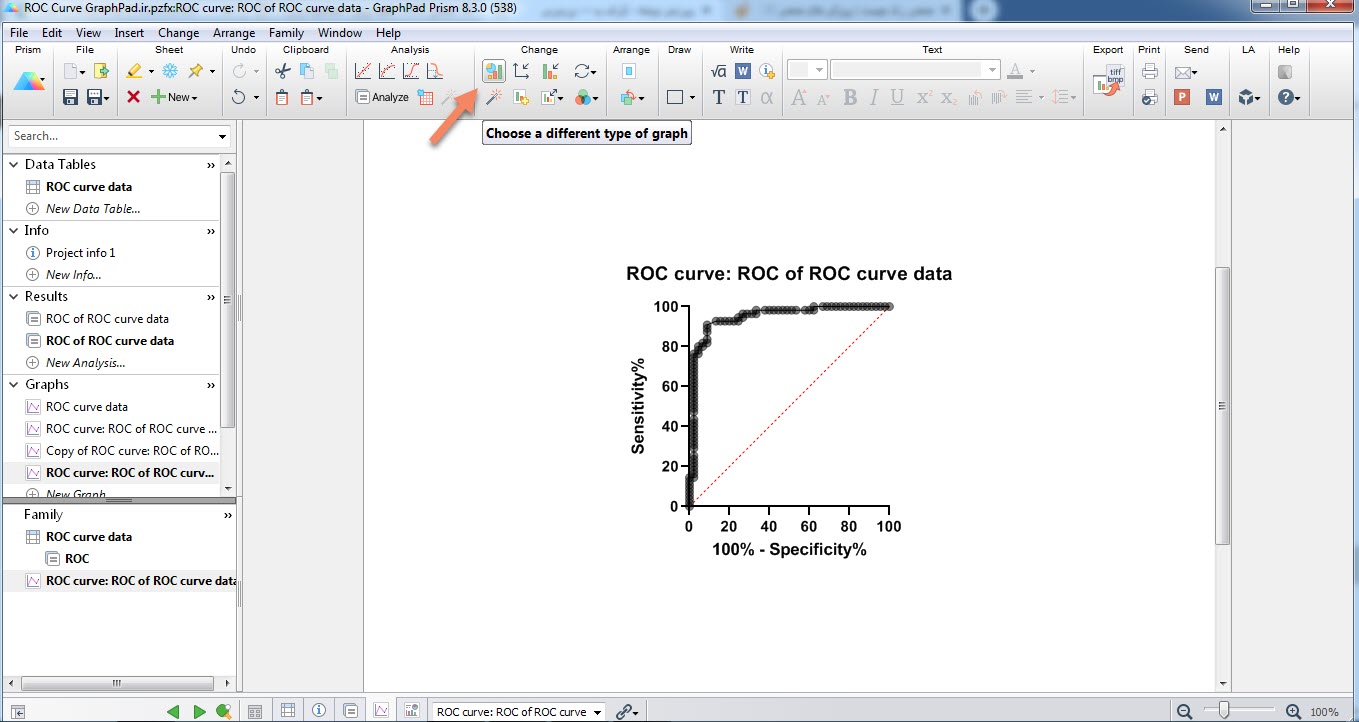
در پایان OK کرده و به بیان نتایج نرمافزار میپردازیم. در ابتدا در فولدر Graphs از پنجره سمت چپ نرمافزار (Navigator Panel)، میتوان منحنی راک رسم شده برای این دادهها را مشاهده کرد. این منحنی را در مطالب قبلی مشاهده کردیم. گراف پد به صورت پیش فرض منحنی زیر را رسم میکند.
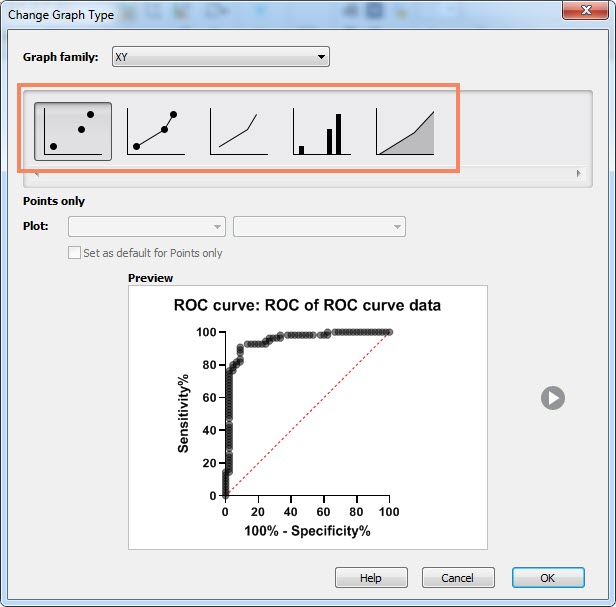
چنانچه تمایل داشته باشیم نحوه نمایش و قالب گراف را عوض کنیم، در بالای منحنی و در منوی Change با انتخاب گزینه Choose a different type of graph میتوان قالبهای دیگر نمایش ROC Curve را انتخاب کنیم. این قالبها را میتوانید در تصویر زیر مشاهده کنید. با کلیک کردن بر روی هر قالب، میتوان آن را مشاهده کرد.
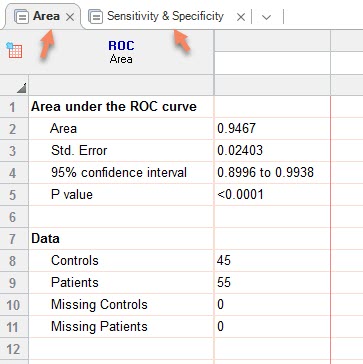
حال بیایید به بررسی نتایج به دست آمده از تحلیل ROC Curve در نرمافزار گراف پد بپردازیم. برای این منظور در فولدر Results از پنجره راهبری شیت با نام ROC of ROC curve data را باز میکنیم. نتایج این شیت در دو زیانه با نامهای Area و Sensitivity & Specificity به صورت زیر آمده است.
ابتدا به توضیح زبانه Area میپردازیم. همانگونه که در تصویر بالا میبینید این زبانه دارای دو بخش به صورت زیر است.
- Area under the ROC curve.
اندازه عددی AUC و یا همان مساحت زیر نمودار راک در این بخش امده است. عدد 0.9467 بیانگر آن است که تست ما تا حد زیادی دارای عملکرد مناسبی در شناسایی صحیح افراد سالم و بیمار است. انحراف معیار خطا و فاصله اطمینان 95 درصد برای همین آماره AUC در ادامه آمده است. گراف پد این دو آماره را بر مبنای یک روش ناپارامتری که مبتنی بر توزیع دادهها در گروههای Control و Patients نیست، به دست میآورد. در این زمینه میتوانید لینک را ببینید.
سوالی که در این بخش میتواند مطرح باشد این است که P value به دست آمده در اینجا چیست؟ بارها به این نکته اشاره شده است که هر کجا و در نتایج هر نرمافزاری با P value یا مقدار احتمال روبهرو شدید، به دنبال آزمون و فرضیه مبتنی بر آن مقدار احتمال باشید. در اینجا نیز ما با فرضیات زیر روبهرو هستیم. در واقع P value حاصل آزمون فرضیه زیر است، به آن دقت کنید.
خُب، حال سوال این است که این فرضیه چیست؟ بیایید از فرض صفر و برابر 0.5 بودن AUC شروع کنیم. در مطالب قبلی عنوان کردیم که اگر در منحنی راک، همه دادهها روی خط نیمساز باشند یعنی نرخ مثبت صحیح و نرخ مثبت کاذب با یکدیگر برابر باشد، بنابراین مساحت زیر منحنی راک یا همان AUC برابر با 0.5 خواهد شد. پس فرض صفر به معنای آن است که تست تشخیصی ما دارای اندازهای برابر هم در نرخ مثبت کاذب و هم در نرخ مثبت صحیح باشد. همانگونه که در تفسیر جدول AUC بیان کردیم، اندازه عددی 0.5 برای AUC به معنای بیفایده و غیرقابل استناد بودن آن تست تشخیصی است.
پس به عبارت سادهتر فرض صفر به معنای آن است که تست تشخیصی ما که قرار است افراد بیمار و سالم را از یکدیگر جداکند، به درد نمیخورد و قدرت جداکنندگی به درستی پایین و به عبارت بهتر شانسی دارد ( از هر دو مورد یکی را درست و دیگری را اشتباه تشخیص میدهد.) با این حساب تعریف فرض مقابل نیز به دست میآید. اندازه عددی AUC مخالف با 0.5 به معنای آن است که تست ما توانایی مناسبی جهت تشخیص بیماری و سلامت در بین افراد اندازهگیری شده را دارا است.
به این ترتیب راز P value در تحلیل ROC Curve کشف میشود. مقدار احتمال به دست آمده به ما کمک میکند تا بتوانیم فرض صفر را پذیرفته و یا رد کنیم. در این مثال اندازه P value برابر با 0.001> شده است. بنابراین به وضوح و در سطح معنیداری پنج درصد فرض صفر رد میشود و میپذیریم که تست مورد استفاده در این مثال، توانایی مناسبی جهت تشخیص بیماری و سلامت در افراد اندازهگیری شده، دارد. البته این مطلب بدون مشاهده P value نیز قابل فهم بود. علاوه بر اینکه خود Area عدد بالایی (0.9467) به دست آمده است، کران پایین فاصله اطمینان Area یعنی (0.8996) نیز همچنان با 0.5 فاصله زیادی دارد.
- Data. در این بخش به سادگی تعداد افراد بیمار، سالم و موارد نامعلوم از آنها یعنی همان Missing نیز آمده است. مطلب خاصی ندارد.
حال بیایید به زبانه دیگر نتایج، یعنی Sensitivity & Specificity بپردازیم. در جدول زیر این نتایج آمده است. در ادامه به توضیح آنها میپردازیم.
این جدول نتایج کاملی از نقطه برش و یا همان Cutoff در ستون اول، حساسیت، ویژگی و فواصل اطمینان 95 درصدی آنها به همراه نسبت درستنمایی، ارایه میکند. یک ردیف را رنگی کردهایم، به توضیح آن میپردازیم. با فهم آن بقیه سطرها نیز فهمیده خواهد شد.
خُب، در سطر رنگی شده و در ستون اول آن عبارت 95.05 < نوشته شده است. حتماً میپرسید به معنای چیست و به چه چیزی اشاره میکند. پاسخ این است که بر مبنای این نتیجه، نقطه برش، عدد 95.05 خواهد بود و اعداد بیشتر از این عدد در تست تشخیصی به عنوان بیمار و اعداد کمتر از آن سالم، تشخیص داده میشوند. عدد 98.18 در Sensitivity نشان میدهد که اگر ما 95.05 را به عنوان نقطه برش بپذیریم، در آن صورت حساسیت تست برابر با 98.18 درصد خواهد شد. به همین ترتیب ویژگی این تست با در نظر گرفتن نقطه برش 95.05 برابر با 37.78 درصد میشود. فواصل اطمینان نیز برای حساسیت و ویژگی به ازای این نقطه برش، آمده است.
سعی میکنیم خودمان این اعداد را به دست آوریم. به هر حال فهم دقیق این مطلب به ما در درک بهتر منحنی ROC کمک خواهد کرد.
فرض کنید Cutoff تست ما همان عدد 95.05 باشد. پس افراد بیشتر از این عدد بیمار و کمتر از این عدد سالم تشخیص داده میشوند. حال بیایید به اعداد واقعی و مشاهده شده نگاه کنیم. در شیت دادهها و در ستون Patients تعداد 55 بیمار قرار دارد. در بین آنها تنها یک نفر دارای عدد کمتر از 95.05 (سطر شماره 29) و بقیه 54 نفر دارای عدد بیشتر نقطه برش هستند. در بین افراد سالم و در ستون Control نیز 17 نفر کمتر از نقطه برش و بقیه 28 نفر بالاتر از نقطه برش 95.05 هستند. بنابراین به سادگی میتوان جدول مشاهده / واقعیت را که در ابتدای متن از آن نام بردیم، در اینجا رسم کرد.
بر مبنای این جدول و نقطه برش 95.05 بیایید اندازههای حساسیت و ویژگی را به دست آوریم. در ادامه میتوانید آن را مشاهده کنید.
به وضوح میتوانید اندازههای 98.18% برای حساسیت و 37.78% برای ویژگی به ازای نقطه برش 95.05 را مشاهده کنید.
به همین ترتیب نرمافزار گراف پد به ازای هر نقطه برش که اندازههای بیشتر از آن بیانگر تشخیص بیماری و اندازههای کمتر از آن نشاندهنده تشخیص سلامت میباشد را مشاهده کنید.
در همینجا بیایید توضیحی هم درباره نسبت درستنمایی بدهیم. این عدد به صورت رابطه زیر به دست میآید.
به عبارتی نسبت درستنمایی حاصل تقسیم محور عمودی به محور افقی در هر آرایه منحنی ROC است.
در تحلیل ROC Curve یک سوال مهم وجود دارد. سوال این است که بالاخره ما کدام نقطه را به عنوان بهترین نقطه برش و Cutoff بپذیریم. همانگونه که در زبانه Sensitivity & Specificity مشاهده میکنید به ازای هر نقطه برش، اعداد مربوط به حساسیت و ویژگی آن آمده است، اما یافتن بهترین نقطه برش بسیار مهم است. این نقطه باید عددی باشد که حساسیت و ویژگی آن بیشترین باشند.
جهت تعیین Cutoff بهینه ما با شاخصی به نام شاخص یودن Youden روبهرو هستیم. بر مبنای این شاخص، نقطه برشی بهینه و مطلوب ما است که مجموع حساسیت و ویژگی آن بیشترین باشد. دقت در نتایج بالا نشان میدهد عدد 109.5 با Sensitivity برابر با 90.91% و Specificity برابر با 91.11% در سطر 41 میتواند به عنوان بهترین نقطه برش مطرح باشد.
چنانچه عدد 109.5 را به عنوان Cutoff این مثال و تست تشخیصی بپذیریم، به معنای آن است که برای هر فردی که عدد اندازهگیری شده بالای 109.5 به دست بیاید آن فرد را بیمار و برای هر فردی که کمتر از 109.5 به دست بیاید آن فرد را سالم در نظر میگیریم. این نقطه برش میتواند تا 91 درصد افراد بیمار را به درستی بیمار تشخیص دهد و تقریبا به همان اندازه 91 درصد افراد سالم را سالم تشخیص دهد. این اندازهها و درصدهای درستی مقادیر بالایی هستند و بیانگر آن هستند که ما توانستهایم نقطه برش بهینه و خوبی به دست آوریم. از طرف دیگر در مطالب قبلی نیز به این نتیجه رسیدیم که تست مورد استفاده در این مثال، توانایی مناسبی جهت تشخیص بیماری و سلامت در افراد اندازهگیری شده، دارد (P value < 0.001).
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2021). ROC curve, cut-off point, sensitivity and specificity using GraphPad Prism software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/roc-curve/.php
For example, if you viewed this guide on 12th January 2022, you would use the following reference
GraphPad Statistics (2021).ROC curve, cut-off point, sensitivity and specificity using GraphPad Prism software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/roc-curve/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.