رگرسیون حداقل مربعات جزئی Partial Least Squares Regression (PLS) با SPSS
روش رگرسیون حداقل مربعات جزئی، که از آن به عنوان طراحی ساختار نهفته Projection to Latent Structure نیز نام برده میشود. یک تکنیک پیشبینیکننده است که جایگزینی برای رگرسیون حداقل مربعات معمولی (OLS)، همبستگی کانونی Canonical Correlation و مدلسازی معادلات ساختاری Structural Equation Modeling (SEM) میباشد، و بهویژه زمانی مفید است که کمیتهای پیشبینیکننده (X) همبستگی بالایی دارند یا زمانی که تعداد پیشبینیکنندهها از تعداد موارد (n) بیشتر باشد.
رگرسیون حداقل مربعات جزئی (PLS) یک روش رگرسیون سریع، کارآمد و بهینه بر اساس کوواریانس است و معمولاً هنگامی استفاده میشود که Variableهای توضیحی زیادی که احتمالاً با یکدیگر همبسته هستند، در مطالعه وجود دارند. در زمینه همبسته بودن کمیتها میتوانید لینک (تشخیص هم خطی Collinearity Diagnostics در مدل های رگرسیونی) را مشاهده کنید.
رگرسیون PLS روشی است که Variableهای مورد استفاده برای پیشبینی را به مجموعه کوچکتری از پیشبینی کنندهها کاهش میدهد. سپس از این مجموعه کوچک شده، برای انجام یک رگرسیون استفاده میشود. به این مجموعههای کوچک شده که از روی Independent Variableها ساخته میشود فاکتورهای نهفته Latent Factors گفته میشود. به همین دلیل است که نام دیگر Partial Least Squares Regression، طراحی ساختار نهفته Projection to Latent Structure است.
رگرسیون حداقل مربعات جزئی
Partial Least Squares regression (PLS)
PLS ویژگیهای تحلیل مولفههای اصلی Principal Component Analysis (PCA) و رگرسیون چندگانه Multiple Regression را ترکیب میکند. ابتدا مجموعهای از عوامل نهفته Latent Factors را به دست میآورد که تا حد امکان بیشترین کوواریانس بین کمیتهای مستقل و وابسته را توضیح دهد. این بخش همان کاری است که PCA انجام میدهد. در مرحلهی بعد، مدل رگرسیون چندگانه بین مقادیر کمیت وابسته و Latent Factors را ایجاد میکند.
ایده رگرسیون PLS این است که با شروع از جدولی با n مشاهده توصیف شده توسط p کمیت، مجموعهای از h مولفه را با الگوریتمهایی با نام PLS 1 و PLS 2 ایجاد کنیم. برخی از نرمافزارها PLS 1 را از PLS 2 متمایز میکنند. PLS 1 مربوط به حالتی است که تنها یک کمیت وابسته Dependent Variable وجود دارد. همچنین PLS 2 مربوط به حالتی است که چندین کمیت وابسته وجود دارد. واضح است که PLS 1 تنها یک مورد خاص از PLS 2 است.
تفاوتها و شباهتها
تحلیلهایی مانند PLS، OLS، PCA و PCR را میتوان در یک رده قرار داد. آنها به صورت ترکیبی از تحلیلهای رگرسیونی و طراحی مولفهها Component کار میکنند. با اینحال با یکدیگر تفاوتهایی نیز دارند. در واقع هر کدام از آنها در یک ساختار متفاوت از مطالعه مورد استفاده قرار میگیرند.
من در ادامه سعی کردهام به اختصار به بیان تفاوتها و شباهتهای آنها با یکدیگر میپردازم. آموزش هر کدام از آنها را نیز میتوانید در سایت گراف پد مشاهده کنید.
- PLS با OLS
همانگونه که از نام آنها برمیآید، Partial Least Squares Regression (PLS) و Ordinary Least Squares Regression (OLS) از نوع تحلیلهای رگرسیونی هستند. به این معنا که آنها دارای Dependent Variable (DV) و Independent Variable (IV) هستند و ما میخواهیم تاثیر IV ها را بر روی DV به دست بیاوریم. PLS رگرسیون حداقل مربعات جزئی و OLS رگرسیون حداقل مربعات معمولی است. هم PLS و هم OLS به منظور براورد پارامترها از روش حداقل مربعات و مینیمم کردن مجموع مربع خطاها یعنی $ \displaystyle \sum{{e_{i}^{2}}}$ استفاده میکنند.
با این حال تفاوت آنها در این است که PLS تحلیل رگرسیونی را بر روی مولفههای (Component) ساخته شده از روی Independent Variable و Dependent Variable ها انجام میدهند و OLS تحلیل رگرسیونی را بر روی خود Independent Variable ها انجام میدهد.
البته انجام تحلیل OLS نیاز به برقراری پیشفرضهایی دارد که در لینک (پیش فرض های تحلیل رگرسیون خطی Linear Regression) میتوانید مشاهده کنید. از PLS هنگامی که این پیشفرضها برقرار نباشد و به ویژه وجود هم خطی در بین کمیتهای مستقل دیده شود، استفاده میکنیم. آموزش رگرسیون OLS را هم میتوانید در لینک (رگرسیون حداقل مربعات معمولی Ordinary Least Squares regression (OLS)) ببینید.
- PLS با PCA
PCA با نام کامل Principal Component Analysis نامیده میشود. بنابراین به معنای این است که PCA فاقد آنالیز رگرسیونی است. دلیل مطلب نیز این است که ما در این تحلیل فاقد کمیت یا کمیتهایی با نام Dependent Variable هستیم و هر چه که داریم Independent Variable است. در واقع در PCA نمیخواهیم تاثیر IVها را بر روی DV به دست بیاوریم، بلکه میخواهیم از روی IVها به ساختن مولفههای اصلی یا همان Principal Component (PC) بپردازیم. در لینک (تحلیل مولفههای اصلی Principal Component Analysis (PCA)) میتوانید آموزش PCA را مشاهده کنید.
PLS نیز تا آنجا که به موضوع طراحی PC ها مربوط میشود با PCA همگام است و مشابه با آن کار میکند، اما به دلیل اینکه PLS دارای Dependent Variable است، یک گام از PCA جلوتر است و تحلیل رگرسیونی را بر روی PCهای ساخته شده از روی Independent Variable و Dependent Variable ها انجام میدهد.
- PLS با PCR
نام کامل PCR به صورت رگرسیون مولفههای اصلی Principal Component Regression بیان میشود. بنابراین PLS و PCR همانند OLS از نوع تحلیلهای رگرسیونی هستند. به این معنا که آنها دارای Dependent Variable (DV) و Independent Variable (IV) هستند و ما میخواهیم تاثیر IV ها را بر روی DV به دست بیاوریم.
هم PLS و هم PCR تحلیل رگرسیونی را بر روی مولفههای اصلی PC ها انجام میدهند. با این حال تفاوت آنها در نحوه طراحی و ساختن PC ها است. در PLS مولفهها (Component) از روی Independent Variable و Dependent Variable ها ساخته میشوند ولی در PCR مولفههای اصلی فقط از روی Independent Variable ها طراحی میشوند. علاقمند بودید از لینک (رگرسیون مولفههای اصلی Principal Component Regression (PCR)) میتوانید آموزش PCR را مشاهده کنید.
در این مقاله من به دنبال تعریف و کاربرد رگرسیون حداقل مربعات جزئی با استفاده از نرمافزار SPSS هستم. در ادامه مثال این مقاله را مشاهده میکنید. فایل دیتا را میتوانید از اینجا Partial Least Squares Regression دریافت کنید.
مثال Partial Least Squares Regression
Example
یک تولیدکننده نوشیدنی میخواهد بداند ترکیب شیمیایی او چگونه با ارزیابیهای حسی مرتبط است. او 37 نمونه دارد که هر کدام با 17 غلظت از عناصر (Cd, Mo, Mn, Ni, Cu, Al, Ba, Cr, Sr, Pb, B, Mg, Si, Na, Ca, P, K) به دست آمده است. او میخواهد امتیاز رایحه نوشیدنی را بر مبنای 17 عنصر پیشبینی کند.
بنابراین او در مطالعه خود هم دارای Dependent Variable (امتیاز رایحه) و هم تعداد زیادی Independent Variable (17 عنصر مختلف) است. تعداد مشاهدات در مقایسه با تعداد IV ها کم بوده (37 مشاهده) است. در واقع از آنجایی که نسبت نمونهها به پیشبینی کنندهها کم است، تولیدکننده تصمیم میگیرد از رگرسیون حداقل مربعات جزئی PLS استفاده کند.
دادهها و این مثال را میتوانید از لینک (I.E. Frank and B.R. Kowalski (1984). “Prediction of Wine Quality and Geographic Origin from Chemical Measurements by Partial Least-Squares Regression Modeling,” Analytica Chimica Acta, 162, 241 − 251) دریافت کنید.
در تصویر زیر بخشی از دادههای این مثال آمده است.
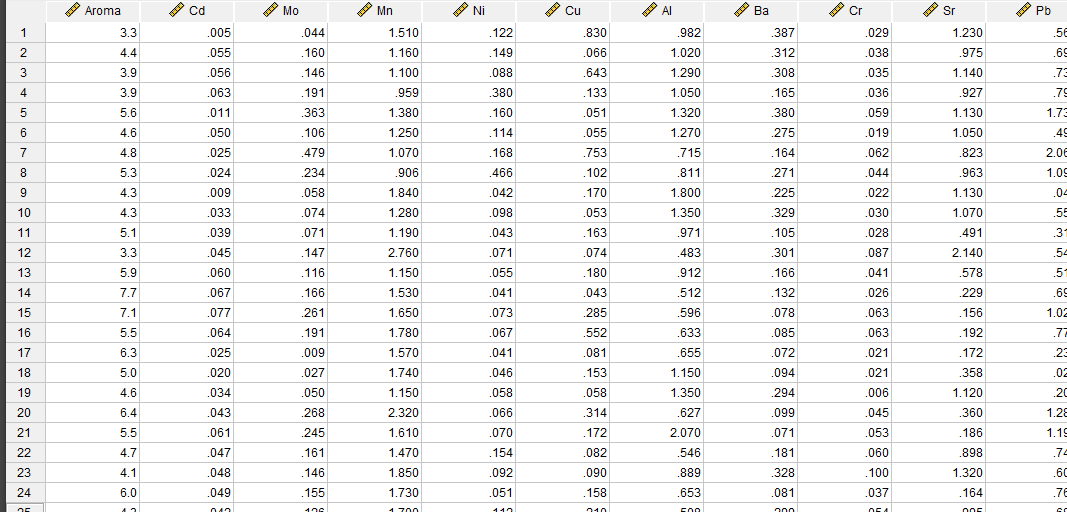
امتیاز رایحه که همان Dependent Variable است در ستون Aroma آمده است. در بقیه ستونها نیز غلظت عناصر مختلف که همان Independent Variable هستند، قرار گرفته است. جهت انجام Partial Least Squares Regression از مسیر زیر در نرمافزار SPSS استفاده میکنیم.
Analyze → Regression → Partial Least Squares
با رفتن به مسیر بالا، پنجره زیر با نام Partial Least Squares Regression برای ما باز میشود. آن را ببینید.
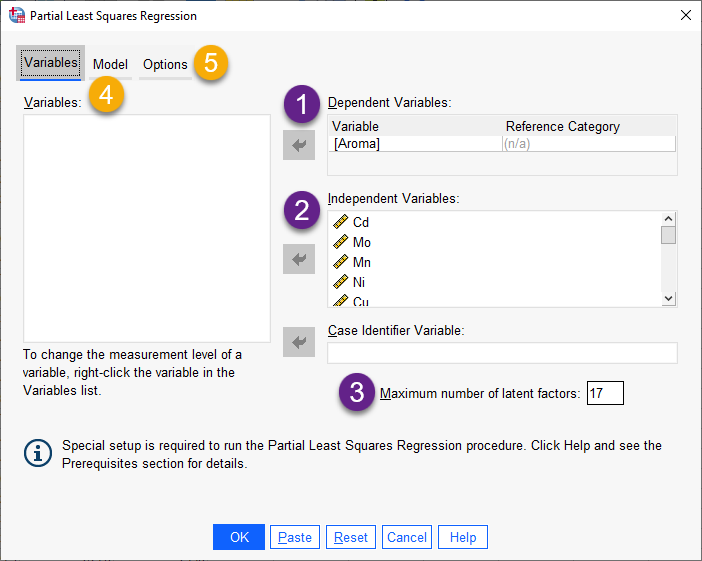
من بخشهای مختلف آن را شمارهگزاری کردهام. در ادامه به توضیح هر یک میپردازم.
1 در کادر Dependent Variables همان کمیت وابسته یعنی امتیاز رایحه نوشیدنی قرار میگیرد. نکته جالب توجه این است که ما در یک مطالعه PLS میتوانیم از Dependent Variable اسمی و یا رتبهای نیز استفاده کنیم. در این حالت یکی از کدها به عنوان Reference Category تعریف میشود. این مطلب به معنای آن است که ما حتی میتوانیم از PLS در تحلیلهای دارای کمیت وابسته باینری (رخداد، عدم رخداد) نیز استفاده کنیم.
2 Independent Variables ها یعنی همان 17 عنصر مختلف در این کادر قرار خواهند گرفت. هدف ما طراحی عوامل نهفته Latent Factors بر روی این کمیتهای مستقل و در مرحله بعد انجام تحلیل رگرسیونی بر روی آنها است.
3 در کادر Maximum number of latent factors حداکثر تعداد عوامل نهفته که در تحلیل PLS قابل دستیابی هستند، نوشته میشود. توصیه من این است که در گام ابتدایی تحلیل تعداد بیشینه قابل دستیابی برای latent factorها را برابر با تعداد Independent Variableهای مطالعه خود قرار دهید. پس از آن و بر مبنای نتایجی که نرمافزار با این انتخاب برای ما قرار میدهد، تعداد latent factor بهینه را به دست خواهیم آورد. بنابراین من فعلاً در این کادر عدد 17 یعنی تعداد کمیتهای مستقل (17 عنصر) را نوشتهام.
4 در تب Model میتوانیم مدل رگرسیونی خود را ببینیم و انتخاب کنیم. پنجره زیر را مشاهده کنید.
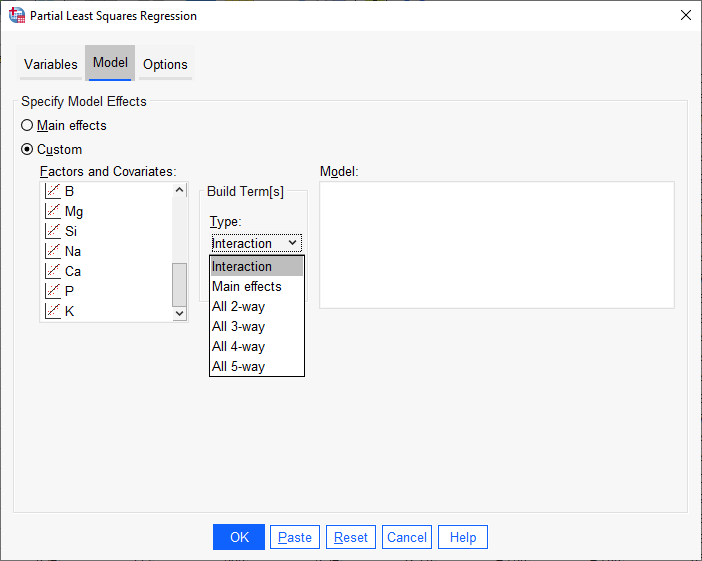
نرمافزار SPSS به صورت پیش فرض بر روی گزینهی Main effects قرار دارد. به معنای اینکه در مدل رگرسیونی فقط اثرات اصلی قرار میگیرد. چنانچه علاقمند باشیم مدل را خودمان بسازیم، مثلاً اثرات متقابل Interaction برخی از کمیتهای مستقل با یکدیگر را هم قرار دهیم، از گزینه Custom استفاده میکنیم. در این گزینه میتوانیم علاوه بر اثرات اصلی، اثرات چندگانه k-way را نیز وارد مدل کنیم.
5 چنانچه علاقمند باشیم یافتهها و نتایج بیشتری از تحلیل PLS خود در نرمافزار SPSS به دست بیاوریم، وارد تب Options میشویم. پنجره زیر را مشاهده کنید.
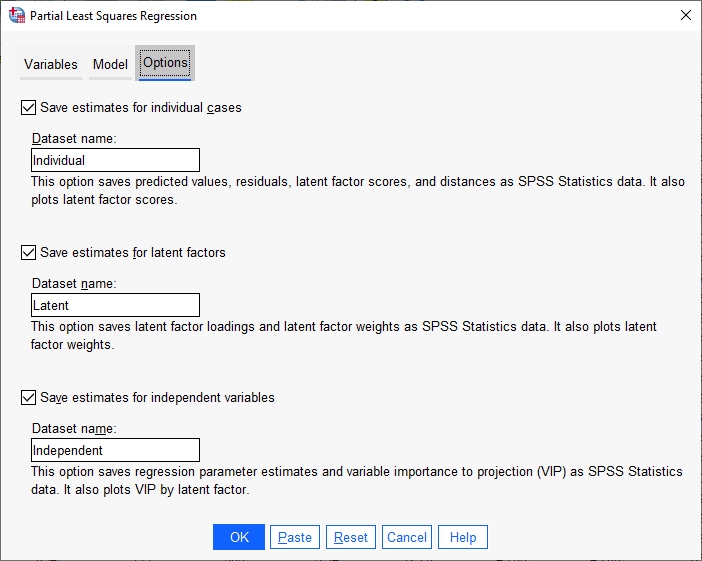
در تب Options میتوانیم براوردهای بیشتری برای هر کدام از مشاهدات Individual Cases، فاکتورهای نهفته Latent Factors و کمیتهای مستقل Independent Variables به دست بیاوریم. این نتایج شامل موارد زیر است.
Save estimates for individual cases. Saves the following casewise model estimates: predicted values, residuals, distance to latent factor model, and latent factor scores. It also plots latent factor scores.
Save estimates for latent factors. Saves latent factor loadings and latent factor weights. It also plots latent factor weights.
Save estimates for independent variables. Saves regression parameter estimates and variable importance to projection (VIP). It also plots VIP by latent factor.
نرمافزار برای Individual Cases یافتههایی مانند مقادیر پیشبینی شده، باقیماندهها، فاصله تا مدل فاکتور نهفته، نمرات فاکتور نهفته و گرافهای مربوط به نمرات فاکتور نهفته را به دست میآورد.
همچنین برای فاکتورهای نهفته بارها و وزنها به همراه نمودار وزنهای فاکتور نهفته، به دست میآید.
برای کمیتهای مستقل نیز براوردهای پارامتر رگرسیونی و اندازه اهمیت هر کمیت برای طرح به دست میآید. همچنین میتوان گرافهای اندازه اهمیت را مشاهده کرد.
دربارهای این نتایج و خروجیهای به دست آمده از تحلیل رگرسیون حداقل مربعات جزئی با استفاده از نرمافزار SPSS، در ادامه بیشتر صحبت خواهیم کرد. نکته مهم در تب Options این است که نرمافزار به صورت پیشفرض این گزینهها را انتخاب نمیکند. بنابراین لازم است ما آنها را انتخاب کرده و از آنجا که قرار است هر کدام از نتایج در فایلهای جدیدی قرار گیرند، برای آنها نام دلخواه قرار دهیم.
نتایج و خروجیهای PLS
Output & Results
حال OK کنید. با انجام این کار در Output و خروجی نرمافزار، نتایج تحلیل PLS به دست میآید.
نکته همانگونه که قبلاً گفتیم این بخش از تحلیلها گام ابتدایی خواهد بود. به دلیل اینکه ما در کادر Maximum number of latent factors حداکثر تعداد عوامل نهفته را برابر با تعداد Independent Variableها یعنی 17 قرار دادهایم. به نظر میرسد این کار چندان منطقی نیست. به دلیل اینکه یکی از اهداف رگرسیون حداقل مربعات جزئی، کاهش تعداد کمیتهای مستقل و دستیابی به فاکتورهای نهفته است. بنابراین اگر قرار باشد تعداد Latent Factorها برابر با Independent Variableها باشد، اصلاً چه نیازی به تحلیل PLS است؟ پاسخ این است که بله ما هم این موضوع را میدانیم که لازم است تعداد فاکتورهای نهفته کمتر از کمیتهای مستقل باشد، با این حال هدف از انجام این کار (برابر قرار دادن Latent Factor با Independent Variable) این است که ما با استفاده از نتایج نرمافزار به کشف و یافتن عدد بهینه برای تعداد فاکتورهای نهفته دست یابیم. همانگونه هم که نوشتیم، این بخش گام ابتدایی تحلیل است و پس از یافتن تعداد فاکتورهای نهفته، بار دیگر تحلیل PLS را انجام خواهیم داد.
در ادامه نتایج و خروجیهای رگرسیون حداقل مربعات جزئی بر مبنای همان عدد 17 برای حداکثر تعداد عوامل نهفته به دست میآید. آنچه در این مرحله برای ما اهمیت دارد و در نکته بالا نیز بیان شد، جدول نسبت واریانس بیان شده Proportion of Variance Explained توسط هر عامل نهفته است. ما بر مبنای نتایج این جدول تصمیم میگیریم که در مرحله بعدی آنالیز از چه تعداد Latent Factor استفاده کنیم.

نکتهای که در انجام تحلیل PLS اهمیت فراوان دارد این است که تعداد عاملهای نهفته باید در یک نقطه بهینه قرار گیرد. به این معنا که کمترین تعداد باشد و از سمت دیگر بتنواند بیشترین واریانس مربوط به کمیت پاسخ را توضیح دهد. در جدول بالا و در ستون Cumulative Y Variance (R-square) میتوانید واریانس تجمعی کمیت پاسخ به ازای اضافه شدن هر فاکتور نهفته را مشاهده کنید.
این جدول نشان میدهد اگر فقط یک عامل نهفته در این مطالعه قرار گیرد، آن عامل میتواند 59.9% واریانس Y (به آن ضریب تعیین یا R-Square هم گفته میشود) را بیان کند. به همین ترتیب اضافه شدن یک عامل دیگر، ضریب تعیین را تا 70.1% افزایش میدهد. اضافه شدن یک عامل نهفته دیگر، ضریب تعیین را هشت درصد دیگر افزایش داده و برابر با 78.2% خواهد بود.
به همین ترتیب اضافه شدن چهارمین فاکتور نهفته ضریب تعیین را فقط 1.7% افزایش میدهد و R-Square مدل PLS برابر با 79.9% به دست میآید. به نظر میرسد ما در این مرحله باید متوقف شویم. به دلیل اینکه بیشتر شدن تعداد فاکتورهای نهفته، ضریب تعیین را به مقدار جزئی افزایش خواهند داد. مثلاً اگر پنجمین فاکتور نهفته نیز اضافه شود، R-Square فقط 1% افزایش پیدا میکند و عدد 80.9% خواهد شد.
از آنجا که هدف ما پیدا کردن تعداد بهینه برای Latent Factor ها است، بنابراین همان سه فاکتور نهفته برای این مطالعه مناسب خواهد بود. بنابراین بار دیگر از مسیر انجام تحلیل رگرسیون حداقل مربعات جزئی به پنجره Partial Least Squares Regression میرویم و اینبار عدد Maximum number of latent factors را برابر با 3 انتخاب میکنیم. تصویر زیر را ببینید.
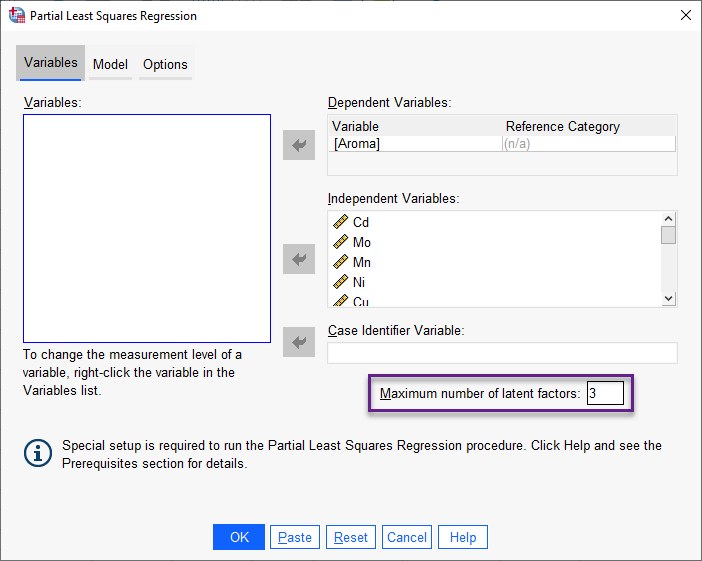
سایر تنظیمات به ویژه در تب Options نیز به همان حالت قبل، قرار میگیرد. حال در ادامه به بیان نتایج، جداول و گرافهای تحلیل رگرسیون حداقل مربعات جزئی که با استفاده از نرمافزار SPSS انجام میدهیم، میپردازیم. این نتایج شامل همه مواردی است که SPSS در رگرسیون PLS در اختیار ما قرار میدهد.
در ابتدا همان جدول Proportion of Variance Explained که در بالاتر از آن نام بردیم دیده میشود. این جدول این بار برای سه فاکتور پنهان به دست آمده است.
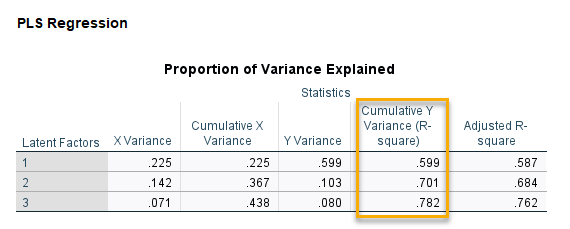
این جدول نشان میدهد، چهار فاکتور نهفته به دست آمده، میتوانند 78.2 درصد پراکندگی و واریانس کمیت پاسخ یعنی امتیاز رایحه را بیان کنند.
جدول بعدی با نام Parameters به محاسبه ضرایب رگرسیونی هر کمیت مستقل Independent Variable بر روی کمیت پاسخ، میپردازد. این نتایج از یک مدل رگرسیونی حداقل مربعات جزئی بین امتیاز رایحه (Y) با 17 عنصر مورد بررسی (Xها) به دست میآید. به رگرسیون خطی علاقمند بودید، این لینک (رگرسیون خطی Linear Regression در نرمافزار SPSS) را ببینید.
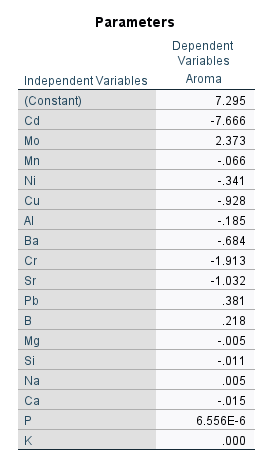
ضرایب مثبت در این جدول، نشاندهنده تاثیر مثبت افزایش غلظت آن عنصر بر روی امتیاز رایحه است و ضرایب منفی بیانگر تاثیر منفی افزایش غلظت آن عنصر بر روی امتیاز رایحه است. در مواردی هم که نزدیک به صفر هستند، نشاندهنده تاثیر ضعیف و اندک عنصر بر امتیاز رایحه نوشیدنی است.
به عنوان مثال این جدول نشان میدهد عنصر کادمیوم Cd تاثیر منفی (B = -7.666) بر رایحه نوشیدنی دارد. با این حال عنصر مولیبدن Mo تاثیر مثبت (B = 2.373) بر رایحه نوشیدنی دارد. بقیه موراد را نیز میتوانید در جدول بالا مشاهده کنید.
با این حال به این نکته دقت کنید که اگر ما تعداد فاکتورهای نهفته را برابر با عدد 17 یعنی همان تعداد Independent Variable ها قرار میدادیم نتایج جدول Parameters همانند نتایج رگرسیون حداقل مربعات معمولی Ordinary Least Squares regression (OLS) به دست میآمد.
جدول بعدی در نتایج با نام اندازه اهمیت کمیت در طرح Variable Importance in the Projection معرفی میشود. آن را ببینید.
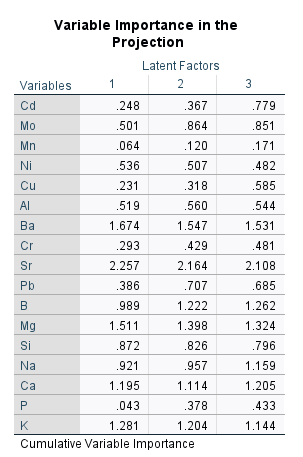
این جدول در تحلیل PLS و تشکیل فاکتورهای نهفته بسیار مهم است و به ما کمک میکند تا دریابیم هر Independent Variable بهتر است در کدام Latent Factor قرار گیرد. به عبارتی با استفاده از نتایج این جدول میتوانیم اجزای تشکیل دهنده هر فاکتور نهفته را دریابیم. روش کار و نحوه تشخیص قرار گرفتن هر کمیت مستقل در فاکتور نهفته این است که نگاه میکنیم عدد کمیت مستقل برای کدام Latent Factor از همه بیشتر است. در هر کدام که بیشتر بود در همان فاکتور نهفته قرار میگیرد.
به عنوان مثال برای کمیت مستقل Cd که همان عنصر کادمیوم بود، این عنصر بهتر است در Latent Factor شماره 3 قرار گیرد. به دلیل اینکه اندازه اهمیت Cd در فاکتور نهفته شماره 3 از همه بیشتر و برابر با 0.779 است. به همین ترتیب ما بر مبنای جدول بالا، میتوانیم عناصر تشکیل دهنده هر فاکتور نهفته را به صورت زیر به دست بیاوریم.
-
- Latent Factor (1). Ni, Ba, Sr, Mg, Si, K
- Latent Factor (2). Mo, Al, Pb
- Latent Factor (3). Cd, Mn, Cu, Cr, B, Na, Ca, P
در ادامه نتایج نرمافزار، جداول مهم وزنها Weights و بارها Loadings دیده میشوند. اجازه دهید ابتدا از جدول بارها شروع کنیم. در تصویر زیر میتوانید آن را ببینید.
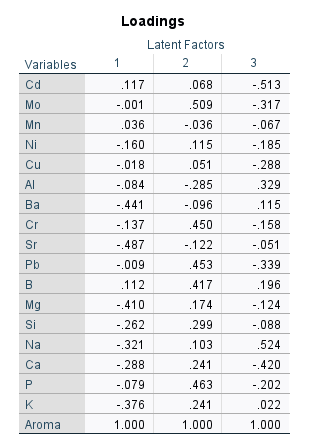
اعداد این جدول ضرایب رگرسیونی بین هر عنصر با فاکتور نهفته است. به این ترتیب بین به ازای هر Latent Factor یک رابطه خطی ایجاد میشود. به عنوان مثال برای Latent Factor (1) رابطه رگرسیونی زیر را خواهیم داشت.
$ \displaystyle 0.117Cd-0.001Mo+0.036Mn-160Ni-0.18Cu-0.084Al……$
بنابراین ضرایب جدول Loadings میتواند اندازه تاثیر هر عنصر در هر فاکتور نهفته را نشان دهد. حال سوال مهم این است که این رابطه رگرسیونی چه چیزی را نشان میدهد؟ یعنی Y آن یا همان کمیت وابسته آن چیست؟ پاسخ این است که این رابطه، اندازههایی به نام X-Score را بیان میکنند. X-Score در کنار Y-Score به عنوان نمرات فاکتور نهفته Latent Factor Scores نامیده میشوند. بعداً و بر روی فایل دیتا که از خروجیهای تحلیل PLS میباشد، در این زمینه بیشتر صحبت میکنیم.
به هر حال اعداد جدول Loadings که ضرایب رگرسیونی مدل بین عناصر و Latent Factor Scores هستند، اثر مثبت و یا منفی هر عنصر بر روی فاکتور نهفته را نشان میدهند. از آنجا که مطالعه ما دارای سه فاکتور نهفته است، بنابراین جدول Loadings نیز دارای سه ستون به ازای هر کدام از Latent Factorها میباشد.
با فهم جدول Loadings، درک جدول Weights نیز ساده خواهد بود. اعداد جدول وزنها، کوواریانس بین عناصر به عنوان کمیتهای مستقل با امتیاز رایحه به عنوان کمیت وابسته را نشان میدهند. این نتایج به تفکیک به ازای هر فاکتور نهفته به دست آمده است. در تصویر زیر آن را ببینید.
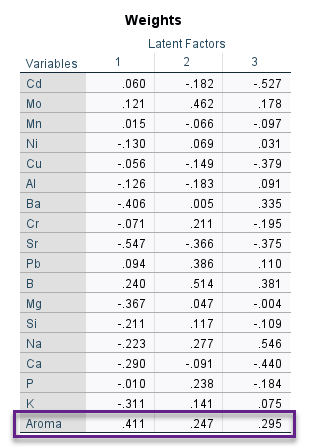
در این جدول سطر مربوط به کمیت وابسته یعنی Aroma که همان امتیاز رایحه را در این مثال نشان میداد، کارکردی مانند اعداد جدول Loadings دارد. به معنای اینکه ضریب رگرسیونی بین کمیت وابسته با اعداد Latent Factor Scores و به بیان دقیقتر Y-Score را نشان میدهد.
نکتهای که در این میان وجود دارد این است که معمولاً علامت مثبت و منفی عناصر در جداول Weights و Loadings مشابه با هم است. اگر در مواردی نیز تفاوت مشاهده شود در اعداد نزدیک به صفر است.
گرافها و نمودارهای PLS
Graphs & Plots
در ادامه نتایج و خروجیهای نرمافزار، نمودارها و گرافهای تحلیل رگرسیون حداقل مربعات جزئی به دست آمده است. ما در ادامه دربارهی این نمودارها توضیح میدهیم.
در ابتدا گراف اندازه اهمیت تجمعی Cumulative Variable Importance رسم شده است. این گراف نتیجه همان جدول Variable Importance in the Projection میباشد که در تحلیلهای قبل به آن اشاره شد. در تصویر زیر آن را ببینید.
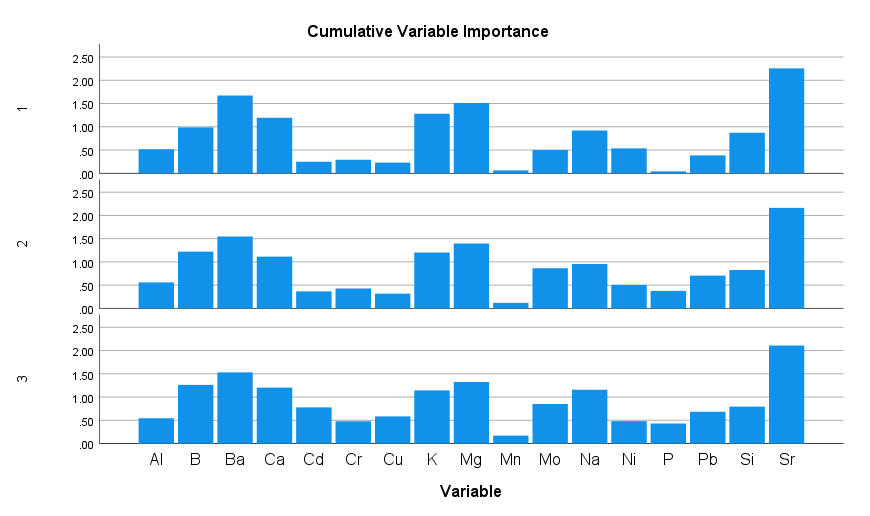
بر مبنای این گراف و جدول مربوط به آن میتوانیم اجزای تشکیل دهنده هر Latent Factor را تعیین کنیم. هر Variable در هر Latent Factor که اندازه اهمیت بیشتری داشته باشد، در همان فاکتور نهفته قرار میگیرد.
گراف دیگر نتایج با نام Regression Plot: Y-Scores vs. X-Scores قرار دارد که در تصویر زیر آمده است.
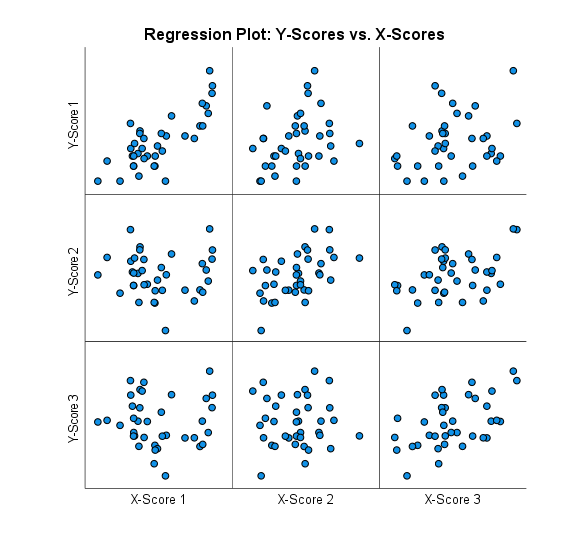
همانگونه که از نام این نمودار برمیآید، این یگ گراف پراکنش Scatter Plot و یا Regression Plot است. در محور عمودی Y-Score ها و در محور افقی نیز X-Score قرار گرفتهاند. از آنجا که ما سه Latent Factor داشتیم، بنابراین در اینجا نیز سه X-Score و Y-Score و در نتیجه 9 Regression Plot داریم.
هر X-Score به ازای Y-Score رسم شده است. نکته مهم این است که بهتر است X-Score به ازای Y-Score متناظر با خود دارای یک روند خطی (صعودی و یا نزولی) باشد و با Y-Score های دیگر فاقد روند قابل مشاهده. به عنوان مثال X-Score 1 که مربوط به فاکتور نهفته 1 است باید با Y-Score 1 رابطه خطی قابل مشاهده داشته باشد و با Y-Score 2 , 3 فاقد رابطه خطی باشد. این مطلب تقریباً در گراف بالا مشاهده میشود و بیانگر مناسب بودن مدل رگرسیون حداقل مربعات جزئی PLS برازش شده است.
به یاد داشته باشید ابتدای بحث عنوان کردیم یکی از دلایل استفاده از PLS وجود هم خطی بین Variable ها است. به این معنی که خود کمیتهای مستقل بر روی یکدیگر اثر میگذارند. به همین دلیل PLS کمیتهای مستقل را به اجزای فاکتورهای نهفته Latent Factor تبدیل میکند به گونهای که خود این فاکتورهای نهفته با یکدیگر هم خطی نداشته باشند. گراف زیر که به آن Scores گفته می شود، ابزاری است جهت قضاوت درباره هم خطی بین فاکتورهای نهفته. در تصویر زیر آن را ببینید.
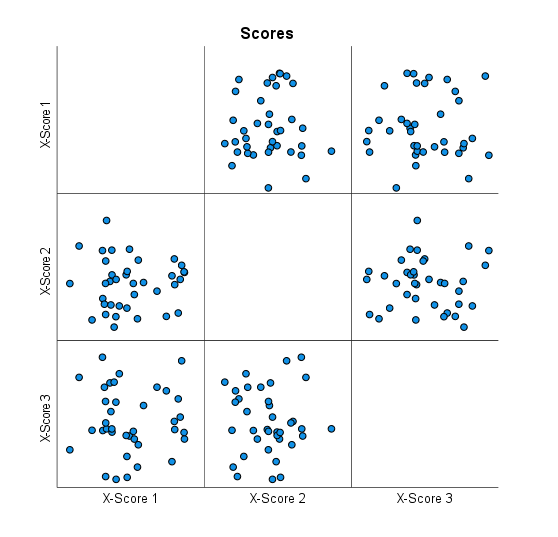
در این گراف که Regression Plot بین هر X-Score با X-Score دیگر رسم شده است، نمودار پراکنش بین آنها آمده است. چنانچه از PLS انتظار داریم که Latent Factor های غیرهم بسته برای ما پیدا کند، باید نمودارهای پراکنش بالا فاقد روند صعودی و یا نزولی باشند و تقریباً به صورت تصادفی قرار گرفته باشند. این نتیجهای است که ما میتوانیم در گراف بالا مشاهده کنیم. در واقع بین هر X-Score با X-Score دیگر، نمیتوانیم روند خاص صعودی و یا نزولی را مشاهده کنیم. این یافتهای خوب است و نشان میدهد مدل رگرسیون PLS ما در این مثال به خوبی کار میکند.
گرافهایی که تا به اینجا مشاهده کردیم مربوط به گزینه Individual Cases در تب Options از تنظیمات نرمافزار بود. در ادامه چند گراف مربوط به گزینه Latent Factors به دست آمده است. در گراف زیر مقادیر جدول Weights به صورت بردار، برای فاکتورهای نهفته 1 و 2 به دست آمده است. در تصویر زیر آن را مشاهده میکنید.
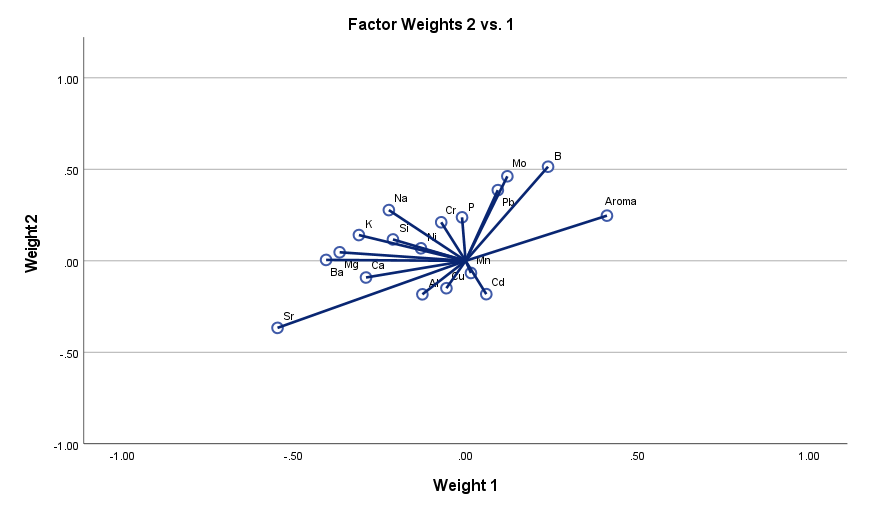
نکته مهم در این گرافها این است که هر خط یا همان بردار نشاندهنده یک عنصر است. البته برای کمیت وابسته Aroma نیز بردار رسم شده است. محور X در این نمودار عدد متناظر با هر کمیت در جدول Weights و برای فاکتور نهفته 1 است و محور Y، عدد متناظر با هر کمیت در جدول Weights و برای فاکتور نهفته 2. همه بردارها نیز از نقطه صفر رسم میشوند.
عناصری که هم X آنها و هم Y مثبت است، بیانگر رابطه مثبت بین آن عنصر با فاکتور نهفته شماره 1 و 2 است، مثل عنصر B. اگر هم X و هم Y نیز منفی باشد، مانند Sr بیانگر رابطه منفی آن عنصر با فاکتورهای نهفته شماره 1 و 2 است. به همین ترتیب برای بقیه عناصر با استفاده از گراف بالا میتوان نحوه اثرگزاری مثبت و یا منفی آن عنصر بر Latent Factor 1, 2 را به دست آورد.
نکته دیگر در این گرافها، طول خط بردار است. هر چقدر طول خط بلندتر باشد به معنای اثر بیشتر بر روی آن فاکتور نهفته است. مثلاً اثر عنصر Pb صرفنظر از مثبت یا منفی بودن آن کمتر از عنصر Mo است.
در ادامه سایر گرافهای Factor Weights رسم شده است. نمودارهای زیر مربوط به جدول وزنها در فاکتورهای نهفته 1 و 3 و همچنین فاکتورهای نهفته 2 و 3 است.
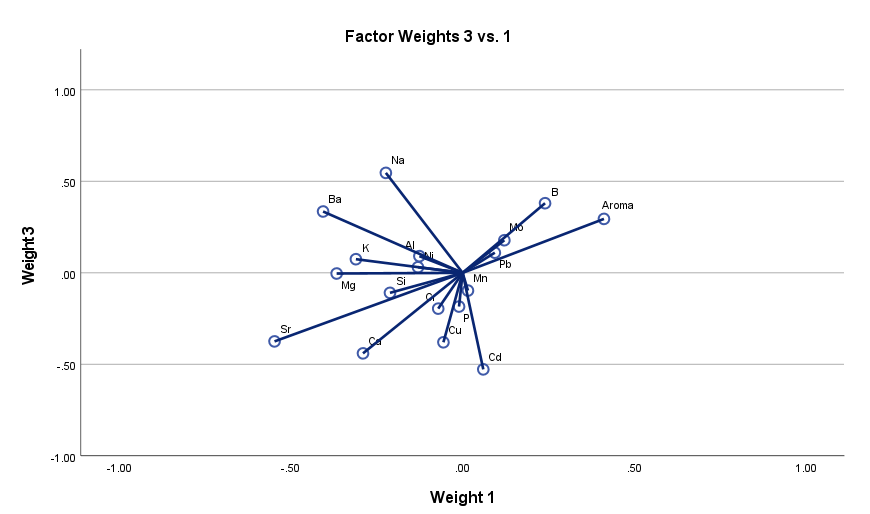
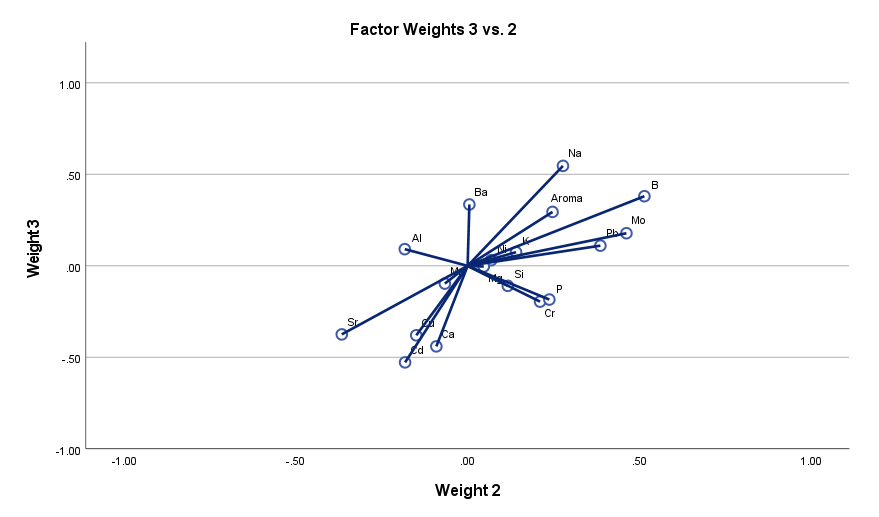
به عنوان مثال در نمودار بردار وزنها برای Latent Factor 2, 3 نتیجه میشود که بیشتر عناصر دارای تاثیر مثبت بر فاکتور نهفته 2 هستند، به دلیل اینکه در سمت راست و بزرگتر از صفر محور X قرار گرفتهاند.
دیتا خروجی PLS
Data
به خاطر داشته باشید در تب Options از پنجره تنظیمات نرمافزار، گزینههایی جهت به دست آوردن خروجیهای مربوط به مشاهدات Individual Cases، فاکتورهای نهفته Latent Factors و کمیتهای مستقل Independent Variables را انتخاب کردیم و برای هر یک نامی نیز انتخاب کردیم. در بخشهای قبلی درباره جداول و گرافهای مربوط به این خروجیها صحبت کردیم، در ادامه دربارهی فایلهای دیتا این نتایج توضیح میدهیم.
پس از انجام تحلیل رگرسیون حداقل مربعات جزئی با استفاده از نرمافزار SPSS، سه فایل دیتای جدید به اسامی همان نامهایی که در تب Options قرار دادیم و نوشتیم، ساخته میشود. من در ادامه هر یک را توضیح میدهم.
- Individual Data
در تصویر زیر میتوانید بخشی از فایل دیتا با نام Individual را مشاهده کنید.
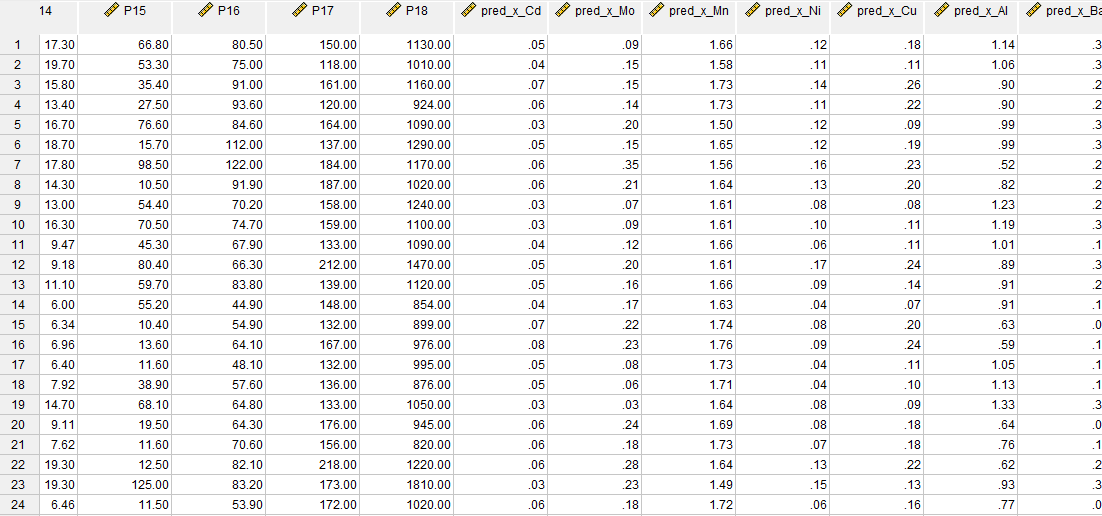
در این فایل ستونهای با نام P1 تا P18 همان اعداد اصلی مطالعه میباشند که یکبار دیگر تکرار شدهاند. P1 همان کمیت وابسته امتیاز رایحه است و P های دیگر، اعداد کمیتهای مستقل.
پس از آن ستونهای با نام pred_x_Cd تا pred_x_K و سپس pred_y_Aroma قرار گرفته است. این ستونها پیشبینی عددی بر مبنای مدل رگرسیون حداقل مربعات جزئی به ازای هر عنصر و همچنین کمیت وابسته امتیاز رایحه هستند. ستونهای بعدی با نام resid که مشاهده میکنند به معنای باقیماندهها یعنی اختلاف بین ستونهای اعداد واقعی P و ستونهای پیشبینی شده pred به ازای هر کدام از کمیتهای مستقل و وابسته هستند.
پس از آنها ستنونهای با اسامی scores_x_1 تا scores_y_3 قرار گرفتهاند. اینها اعداد مربوط به نمرات فاکتورهای نهفته به ازای هر کدام از Latent Factor ها هستند. سه تا X و سه تا Y، به دلیل اینکه ما در مطالعه خود سه فاکتور نهفته طراحی کردیم.
در پایان ستونهای D_Mod_X و D_Mod_Y دیده میشود. D_Mod_X که به آن Distance X نیز گفته میشود، نشان میدهد هر مشاهده با چه اندازه فاصلهای (عددی مثبت) از فضای x که به آن x-space گفته میشود، قرار گرفتهاند. این فواصل مشخص میکنند که مشاهدات تا چه اندازه با X-Score ها توصیف میشوند. هر چقدر این اندازهها کوچک باشند به معنای برازش بهتر مدل رگرسیونی PLS بر آن مشاهده است. بزرگ بودن این اعداد حتی میتواند بیانگر داده پرت outlier بودن آن مشاهده نسبت به مدل رگرسیونی حداقل مربعات جزئی تلقی شود.
به همین ترتیب D_Mod_Y نیز به عنوان Distance Y بیان میشوند. همان تعبیری که در بالا برای D_Mod_X داشتیم اینجا برای D_Mod_Y و نسبت به y-space و Y-Score برقرار است.
نکته نرمافزاری مانند Minitab هنگامی که تحلیل رگرسیون PLS انجام میدهد، نتایجی با نام اهرمها Leverages ارایه میدهد. البته SPSS چنین خروجی ندارد. اهرمها، مشاهدات با مقادیر x غیر معمول یا پرت را شناسایی میکنند. مشاهدات با اعداد Leverages بالا دارای x-score های دور از صفر هستند و میتوانند تأثیر زیادی بر ضرایب رگرسیونی داشته باشند. البته نقاط با اهرم بالا لزوماً در y-space پرت نیستند. در اینجا بیان میشود مشاهدات با مقادیر Leverages بیشتر از 2m / n را بررسی کنید، جایی که m = تعداد فاکتورهای نهفته و n = تعداد مشاهدات است.
- Latent Data
در تصویر زیر میتوانید فایل دیتا با نام Latent را مشاهده کنید.
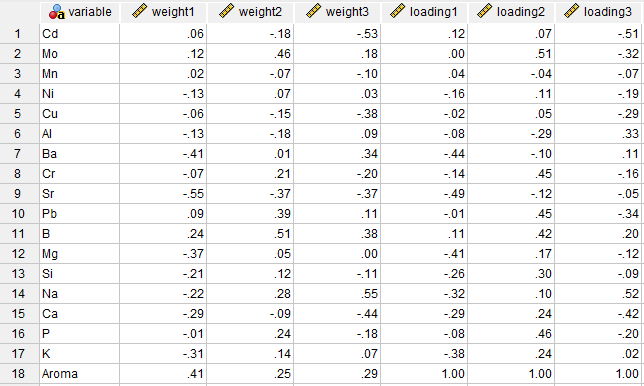
خیلی ساده باید بگوییم این فایل از دیتا و نتایج چیز خاصی ندارد و همان اندازههای عددی به دست آمده به ازای هر کدام از عناصر و کمیت وابسته در جدولهای Weights و Loadings است که بار دیگر اینجا و در قالب یک فایل دیتا آمده است.
- Independent Data
در تصویر زیر میتوانید فایل دیتا با نام Independent را مشاهده کنید.
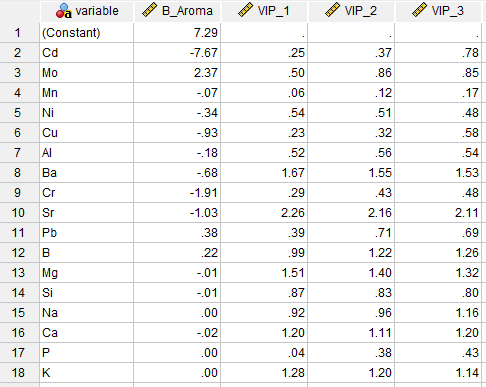
در این فایل دیتا، ستون با نام B_Aroma همان نتایج جدول Parameters است که در آن به محاسبه ضرایب رگرسیونی هر کمیت مستقل Independent Variable بر روی کمیت پاسخ، میپردازیم. ستونهای با نام VIP نیز هر کدام به بیان اندازه اهمیت هر عنصر بر روی کمیت وابسته و به ازای هر Latent Factor اشاره میکند. نتایج این ستونها را قبلاً در جدول Variable Importance in the Projection مشاهده کردیم.
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2022). Partial Least Squares regression using SPSS. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/partial-least-squares-regression-spss/.php
For example, if you viewed this guide on 12th January 2022, you would use the following reference
GraphPad Statistics (2022). Partial Least Squares regression using SPSS. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/partial-least-squares-regression-spss/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.


