مثال آموزشی Ordinary one-way ANOVA با گراف پد
همانگونه که میدانیم هنگامی که بخواهیم بیشتر از دو گروه را با یکدیگر مورد مقایسه قرار دهیم از تحلیلهای ANOVA استفاده میکنیم. نرمافزار گراف پد تحلیلهای ANOVA را در دو دسته Ordinary و Repeated Measure قرار میدهد. تحلیل Ordinary زمانی استفاده میشود که گروهها از یکدیگر مستقل باشند. در واقع این نوع آزمون تعمیم یافته آزمون T Test Unpaired است.
تحلیل Repeated Measure نیز به منظور مقایسه گروههای به هم وابسته و در زمانهای مختلف اندازهگیری شده، استفاده میشود. این نوع آزمون تعمیم یافته آزمون T Test Paired است.
ما در این آموزش قصد داریم درباره آزمونهای ANOVA از نوع Ordinary صحبت کنیم. تحلیل ANOVA از نوع Repeated Measure را میتوانید از اینجا مشاهده کنید. نرمافزار گراف پد، امکانات خوبی جهت انجام فرایند مقایسه بین گروهی چه به صورت ساده و یا پیشرفته، فراهم کرده است.
در مثال زیر با استفاده از نرمافزار گراف پد پریسم، به دنبال مقایسه بین چند گروه مستقل هستیم. در این مثال میخواهیم فرض برابری یا عدم برابری میانگین بین گروههای مختلف را آزمون کرده، مقدار احتمال آزمون را به دست آورده و از یک نمودار ساده جهت بیان تحلیل، استفاده کنیم.
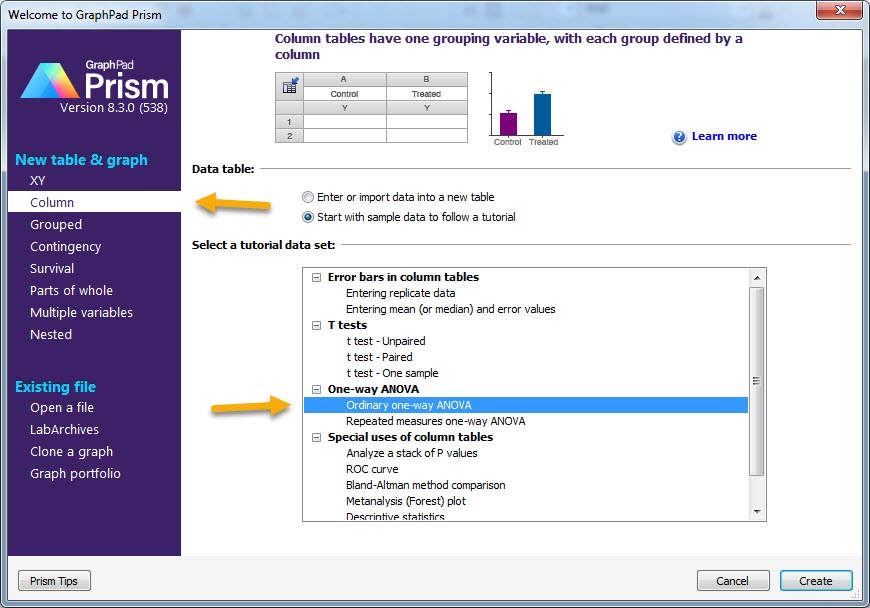
این مثال با نام Ordinary one-way ANOVA در دسته تحلیلهای Column و در بخش One-way ANOVA صفحه ورودی نرمافزار گراف پد قرار دارد. فایل مثال را میتوانید از اینجا دانلود کنید.
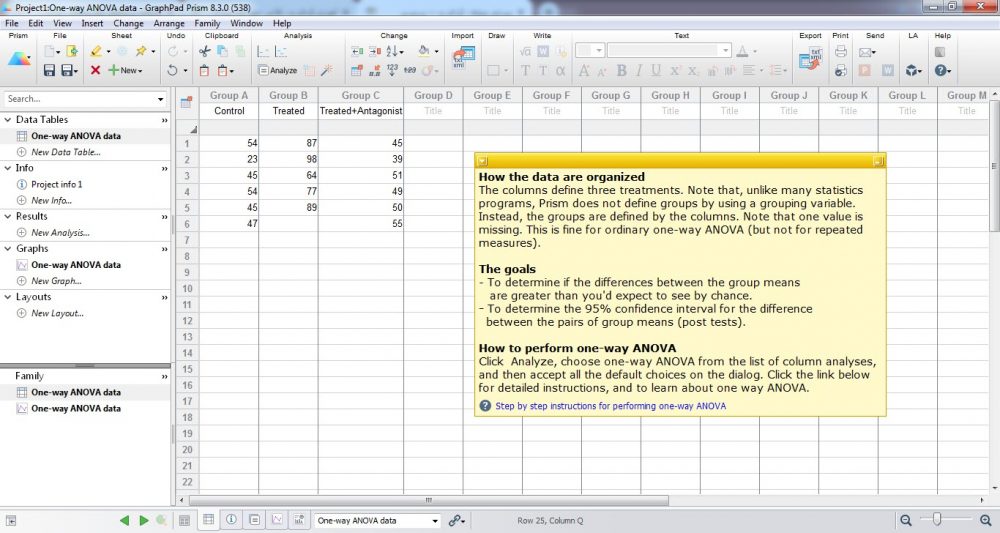
وقتی مثال را Create میکنیم با دادههای زیر روبهرو میشویم. همانگونه که مشاهده میکنید و در Note مثال نیز آمده است، میخواهیم سه درمان Treatments مختلف را که هر یک بر روی نمونههای متفاوت انجام شده است، با هم مقایسه کرده و به این سوال پاسخ دهیم که آیا اختلافی بین درمانهای مختلف وجود دارد یا خیر.
همچنین به دنبال یافتن فاصله اطمینان 95 درصد برای اختلاف بین میانگینها نیز هستیم. همانگونه که بارها بیان کردیم یکی از خوبیهای کار با گراف پد، بیان مسیر گام به گام تحلیل توسط نرمافزار در مثالهای آموزشی آن است.
در این مثال و همانگونه که در بخش How to perform one-way ANOVA از پنجره Note مشاهده میکنید، مراحل قدم به قدم انجام تحلیل آمده است.
ابتدا در بخش Graphs از پنجره سمت راست (Navigator Panel) میتوان انواع نمودارهای قابل رسم توسط نرمافزار را با کلیک بر روی شیت با نام one-way ANOVA مشاهده کرد. همانگونه که میدانید به خوبی میتوان انواع ویرایشهای دلخواه بر روی گراف به دست آمده را اعمال کرد.
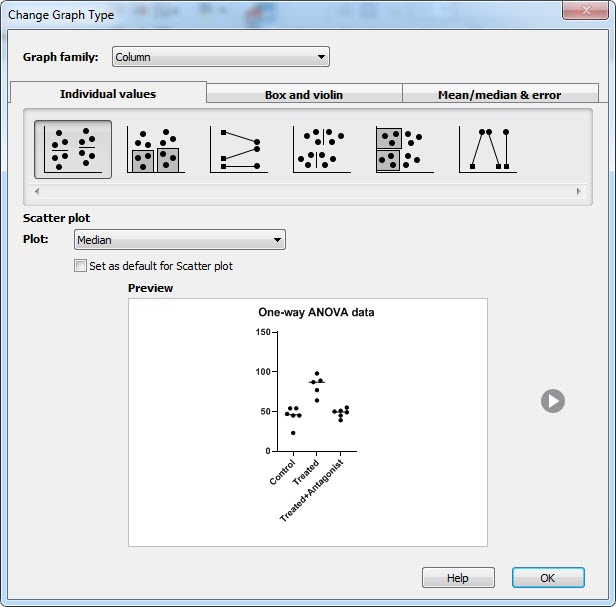
در اینجا در بخش Graph family و در کادر کشویی مقابل آن میتوان نوع نموداری را که میخواهیم رسم کنیم، انتخاب کنیم. از آنجا که در ابتدا این مثال در دسته تحلیلهای Column قرار داشت، بنابراین آن را به همان صورت Column قرار میدهیم.
پس از آن سه تب مختلف با نامهای Box and violin ،Individual values و Mean/median & error دیده میشود. بر روی هر کدام از تبها که کلیک کنیم، میتوان نمودارهای ستونی مرتبط با همان تب را مشاهده کرد.
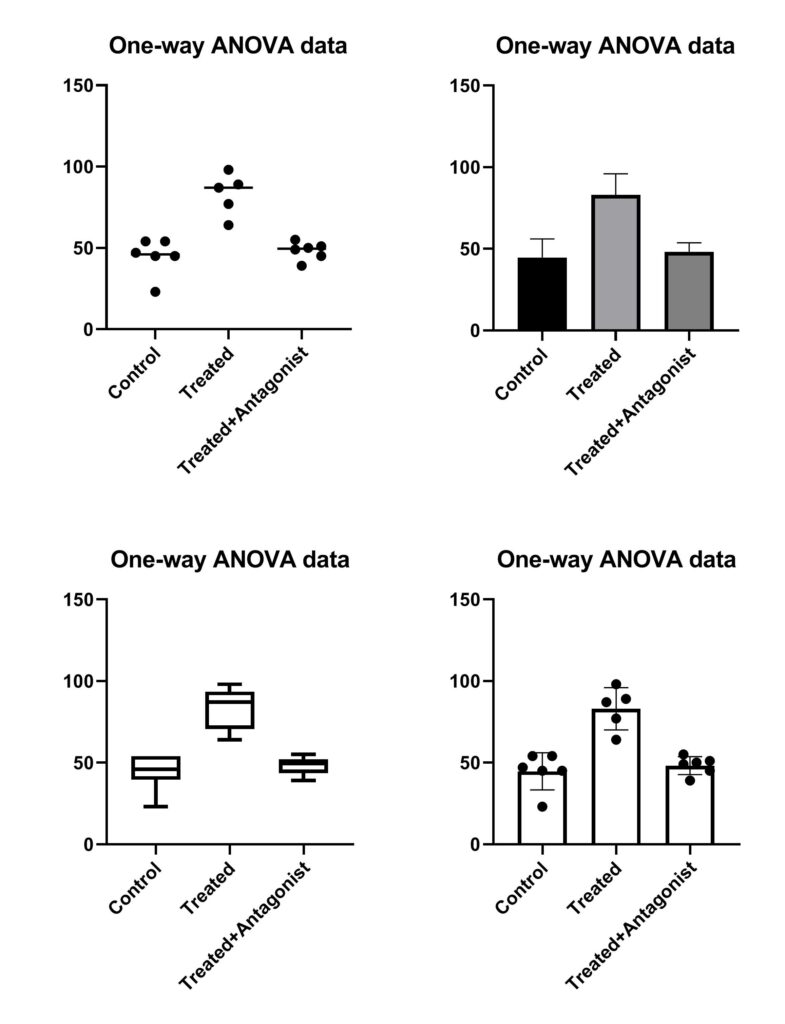
در تصاویر زیر، چندین گراف با استفاده از همین تبها بر روی دادههای مثال Ordinary one-way ANOVA رسم شده است. میتوانید خودتان نیز به سادگی امتحان کرده و این گرافها را به دست آورید. با استفاده از یک layout در گراف پد، این گرافها را در یک تصویر کنار هم قرار دادهایم.
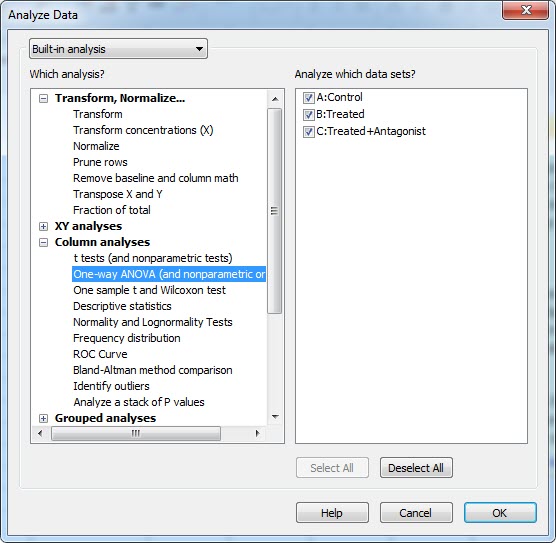
حال بیایید به تحلیل بین گروهها و مقایسه آنها با یکدیگر بپردازیم. از آنجا که میخواهیم میانگینهای چند نمونه مستقل (بیشتر از دو گروه) را با هم مقایسه کنیم، پس تحلیل ما Ordinary one-way ANOVA خواهد بود. جهت انجام این کار در شیت دادهها از منوی Analyze در بالای صفحه، گزینه One-way ANOVA and nonparametric or mixed را انتخاب میکنیم.
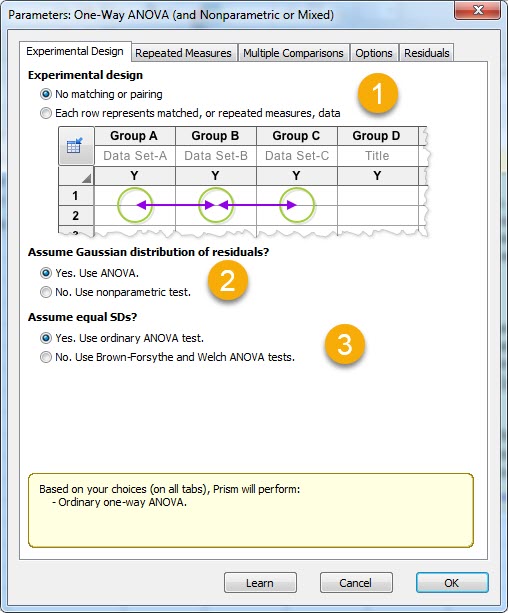
پنجره زیر با نام Parameters: One-way ANOVA and nonparametric or mixed برای ما باز میشود. در اینجا سه بخش انتخابی وجود دارد. در بخش Experimental design انتخاب میکنیم مطالعه ما Matching است یا خیر. اگر تحلیل ما از نوع Ordinary one-way ANOVA باشد یعنی گروهها از هم مستقل باشند ما گزینه No matching or pairing را انتخاب میکنیم. اگر مطالعه ما Repeated Measure one-way ANOVA باشد یعنی گروهها به هم وابسته باشند، گزینه بعدی را انتخاب میکنیم. در این زمینه میتوانید این لینک را ببینید.
در این مثال از آنجا که به دنبال مقایسه سه گروه مستقل هستیم، بنابراین گزینه No matching or pairing را انتخاب میکنیم. به فلشهایی که گراف پد نشان میدهد دقت کنید. فلشها نشان میدهند نماینده هر گروه یعنی میانگین آن با گروه دیگر مقایسه میشود.
در بخش Assume Gaussian distribution of residuals، نرمافزار درباره نرمال بودن یا نبودن توزیع باقیماندهها سوال میپرسد. از آنجا که ANOVA خود یک مدل خطی است بنابراین دارای باقیمانده است. اگر باقیماندهها نرمال باشند از آزمون پارامتری یعنی همان ANOVA استفاده میشود و اگر باقیماندهها غیر نرمال باشند از آزمون ناپارامتری استفاده میکند. بنابراین لازم است به منظور انتخاب صحیح در این بخش، آزمون نرمالیتی را بر روی باقیماندههای این مثال نیز انجام دهیم. در این زمینه در ادامه توضیحات بیشتری میدهیم.
اما در بخش Assume equal SDs به مقایسه واریانس (انحراف معیار) گروهها با یکدیگر میپردازد و بسته به اینکه در بخش قبلی، آزمون پارامتری را انتخاب کنیم یا آزمون ناپارامتری، با گزینههای متفاوتی روبهرو خواهیم بود.
اگر باقیماندهها نرمال باشند و در بخش Assume Gaussian distribution of residuals، گزینه آزمون پارامتری ANOVA انتخاب شود، همانند تصویر بالا Assume equal SDs میتواند شامل گزینههای بله واریانسها برابر هستند پس از آزمون Ordinary one-way ANOVA استفاده کن و گزینه خیر واریانسها برابر نیستند پس از آزمون Brown-Forsythe and Welch ANOVA استفاده کن، قرار گیرند.
همچنین اگر در بخش Assume Gaussian distribution of residuals آزمون ناپارامتری انتخاب شود، دیگر بخش Assume equal SDs را نخواهیم داشت. همانگونه که میدانید آزمون ناپارامتری در این حالت کروسکال-والیس kruskal-Wallis خواهد بود.
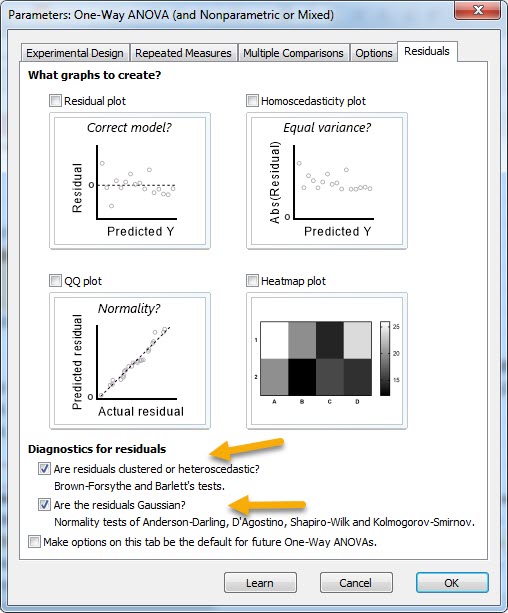
بنابراین انتخاب صحیح بین آزمون پارامتری و ناپارامتری جهت انجام فرایندهای بعدی تحلیل مهم است. از آنجا که هنوز نمیدانیم باقیماندهها نرمال هستند یا خیر، که براساس آن پارامتری یا ناپارامتری بودن آزمون مقایسه را انتخاب کنیم، پس قبل از هر تحلیلی، به تب Residuals میرویم. پنجره زیر برای ما باز خواهد شد.
در این تب و در بخش Diagnostics for residuals هر دو گزینه Are residuals clustered or heteroscedastic و Are the residuals Gaussian را انتخاب میکنیم. انتخاب Are residuals clustered or heteroscedastic جهت انجام آزمون همگنی واریانسها است و آزمون Are the residuals Gaussian جهت بررسی فرض نرمالیتی باقیماندهها استفاده میشود. انتخاب این گزینهها سبب میشود در شیت Result نرمافزار، نتایج آزمون همگنی واریانسها و همچنین نرمال بودن باقیماندهها، مشاهده شوند. پس از آن بر مبنای نتایج به دست آمده تصمیم میگیریم آیا انتخاب آزمون پارامتری ANOVA درست بوده است و یا باقیماندهها نرمال نیستند و باید از آزمون ناپارامتری کروسکال-والیس استفاده شود. همچنین اگر استفاده از آزمون پارامتری ANOVA صحیح است، واریانسها برابر هستند یا خیر.
در بخش Assume equal SDs نیز فعلاً همان گزینه پیشفرض نرمافزار یعنی Yes. Use Ordinary ANOVA test را انتخاب میکنیم. پس از مشاهده نتایج به دست آمده میتوانیم تصمیم بگیریم آیا واریانس گروهها برابر هستند و این انتخاب صحیح بوده است یا اینکه واریانسها برابر نیستند و باید گزینه No. Use Brown-Forsythe and Welch ANOVA tests انتخاب شود.
یک نکته دیگر نیز در این میان اهمیت دارد. چگونه میتوان گروهها را دوبهدو با یکدیگر مقایسه کرد؟ یعنی در این مثال Control را با Treated مقایسه کرد و همچنین Control با Treated+Antagonist مقایسه شود و اگر خواستیم یک مقایسه دوبهدو نیز بین Treated و Treated+Antagonist داشته باشیم.
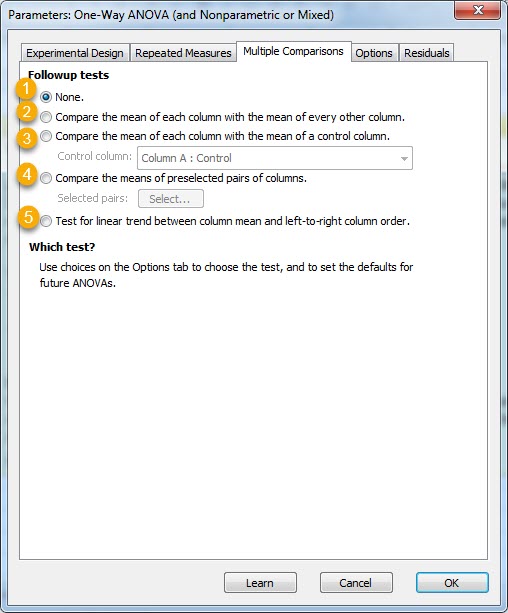
انجام این کار با تب Multiple Comparisons در همین پنجره Parameters: One-way ANOVA and nonparametric or mixed امکانپذیر است. پس بر روی این تب کلیک میکنیم، پنجره زیر باز خواهد شد.
در اینجا میتوانید پنج گزینه مشاهده کنید، ما آنها را به ترتیب بیان میکنیم.
1- None. خُب، با انتخاب این گزینه هیچ آزمون دوبهدویی انجام نمیشود. با این انتخاب فقط یک آزمون کلی ANOVA بین همه گروهها انجام میشود.
2- Compare the mean of each column with the mean of every other column. با انتخاب این گزینه میانگین هر گروه با گروه دیگر مقایسه میشود. به صورت متداول معمولاً این گزینه انتخاب میشود، زیرا کاملترین نوع مقایسه است.
3- Compare the mean of each column with the mean of a control column. با انتخاب این گزینه میتوان میانگین هر ستون را با یک ستون از قبل انتخاب شده که نقش کنترل را بازی میکند، مقایسه کرد. در کادر باز شده به سادگی میتوان این گروه که قرار است بقیه گروهها با آن مقایسه شوند را انتخاب کرد.
4- Compare the means of preselected pairs of columns. با انتخاب این گزینه میتوان فقط مقایسه را به دو گروه انتخاب شده تقلیل داد. این دو گروه را میتوان در باکس Select انتخاب کرد.
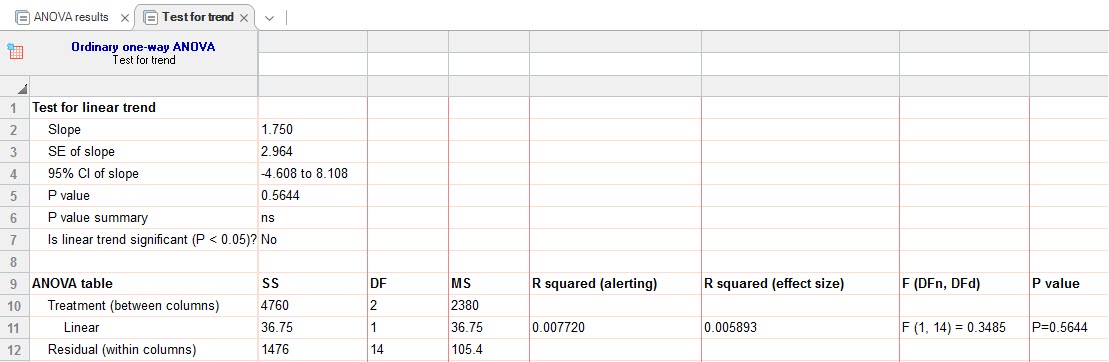
5- Test for linear trend between column mean and left-to-right column order. این گزینه کمتر به کار میآید، با این حال با انتخاب این گزینه آزمون وجود روند خطی بین میانگین ستونها انجام میشود. اگر این گزینه را انتخاب کنیم در شیت نتایج میتوانیم خروجی زیر را ببینیم.
این نتیجه نشان میدهد در میانگین ستونها روند خطی وجود ندارد (P-value = 0.5644).
ما در اینجا همان گزینه Compare the mean of each column with the mean of every other column را انتخاب میکنیم تا بتوانیم همه گروهها را با همدیگر مقایسه کنیم.
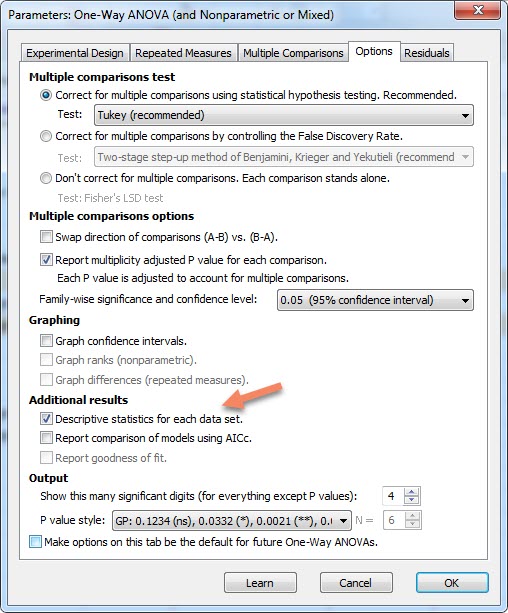
در اینجا خوب است به یک نکته دیگر نیز اشاره کنیم. به دست آوردن آمارههای توصیفی مانند میانگین، انحراف معیار و دامنه اعداد در هر گروه میتوانند یافتههای جالب توجهی باشند. به همین دلیل میتوان در تب Options از پنجره Parameters: One-way ANOVA and nonparametric or mixed و در کادر Additional results گزینه Descriptive statistics for each data set را انتخاب کرد. با انتخاب این گزینه میتوان در خروجی نتایج به دست آمده از گراف پد، انواع آمارههای توصیفی به ازای هر گروه را مشاهده کرد.
با دیگر تنظیمات کاری نداریم و OK میکنیم. نتایج در یک شیت جدید در بخش Results از پنجره سمت راست (Navigator Panel) با نام Ordinary one-way ANOVA of One-way ANOVA data ارایه میشود.
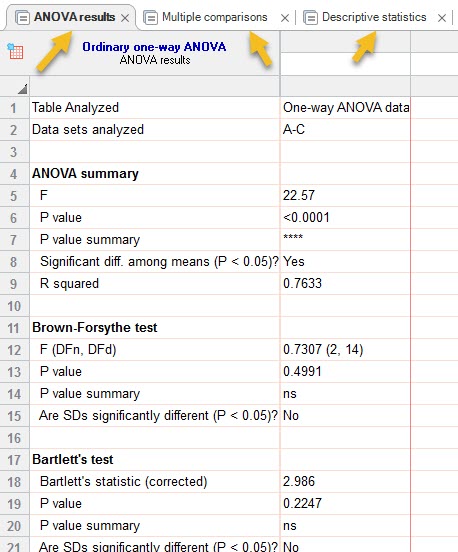
این شیت دارای سه زبانه است. یکی با نام ANOVA results که به ارایه تحلیل مقایسه کلی بین گروهها پرداخته است، یک زبانه با نام Multiple comparisons که به مقایسه دوبهدو بین گروهها پرداخته است. زبانه دیگر با نام Descriptive statistics به ارایه و بیان آمارههای توصیفی هر گروه اشاره دارد.
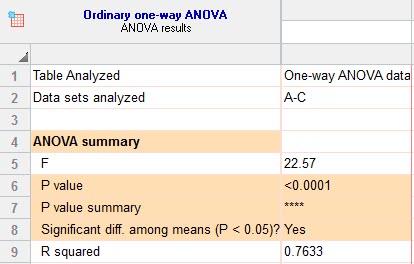
در ابتدا از تب ANOVA results شروع میکنیم. در بخش ANOVA summary و ANOVA table نتیجه مقایسه بین گروهها آمده است و نشان میدهد بین گروهها اختلاف معنادار وجود دارد (P value <0.0001). جدول زیر را مشاهده کنید.
خوب است در همین جا دربارهی ستارههای معناداری در نرمافزار گراف پد پریزم صحبت کنیم. در این نرمافزار با استفاده از ستارهها، قوت و شدت معناداری بیان میشود. در جدول زیر میتوانید مفهوم ستارههای معناداری را مشاهده کنید.
این جدول به معنای آن است که هر چه تعداد ستارهها افزایش یابد مقدار احتمال آزمون کمتر میشود.
چنانچه یادتان باشد در پنجره Parameters: One-way ANOVA and nonparametric or mixed و در بخش Assume Gaussian distribution of residuals درباره نرمال بودن یا نبودن توزیع باقیماندهها صحبت کردیم. حال در اینجا و در کادر Normality of residuals آزمون نرمالیتی باقیماندهها جهت انتخاب پارامتری یا ناپارامتری آزمون مقایسه بین گروهی، انجام شده است.
نرمافزار گراف پد بر مبنای چهار روش آزمون نرمالیتی را انجام میدهد، با این حال توصیه نرمافزار استفاده از روش D’Agostino-Pearson است. در این زمینه میتوانید لینک https://www.graphpad.com/guides/prism/8/statistics/stat_choosing_a_normality_test.htm را ببینید. روش متداول Kolmogorov-Smirnov نیز آمده است. همانگونه که مشاهده میکنید بر مبنای روش توصیهشدهی D’Agostino-Pearson توزیع باقیماندهها نرمال است. مقدار احتمال P-value نشان میدهد، در سطح معنیداری پنج درصد باقیماندهها نرمال هستند. بنابراین استفاده از روش پارامتری (یعنی همین آزمون Ordinary one-way ANOVA) صحیح است.
بنابراین در پنجره Parameters: One-way ANOVA and nonparametric or mixed و در بخش Assume Gaussian distribution of residuals با اطمینان میتوانیم گزینه تایید آزمونهای پارامتری را انتخاب کنیم.
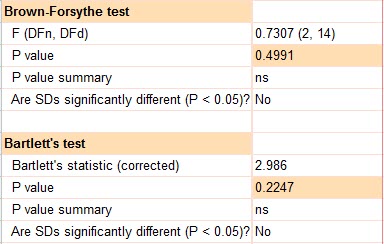
اما هنوز درباره برابری واریانسها (انحراف معیار) اطلاعی نداریم. در همین تب ANOVA results نتایج آزمون همگنی واریانسها آمده است.
همانگونه که در جدول بالا دیده میشود با استفاده از آزمونهای Brown-Forsythe و Bartlett’s بررسی همگنی واریانسها انجام شده است. نتیجه هر دو آزمون نشان میدهد واریانسها اختلاف معناداری با یکدیگر ندارند. بنابراین با اطمینان میتوانیم در بخش Assume equal SDs همان گزینه Yes. Use ordinary one way ANOVA را انتخاب کنیم.
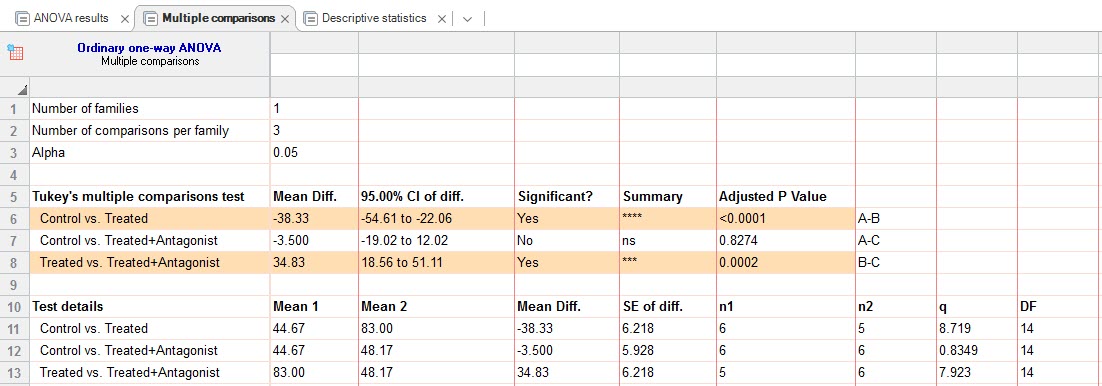
مواردی که در بالا مطرح کردیم دربارهی زبانه ANOVA results بود. مطلبی که همچنان باقی مانده درباره نحوه مقایسه دوبهدو بین گروهها است. این نتایج در زبانه Multiple comparisons آمده است. حال بیایید به توضیح آنها بپردازیم.
در ابتدا و همانگونه که مشاهده میکنید، مقایسههای دوگانه با استفاده از آزمون توکی Tukey انجام شده است. در این مقایسات هر گروه به صورت جداگانه با گروه دیگر مورد مقایسه قرار گرفته است. به عنوان مثال Control با Treated مقایسه شده و اختلاف بین آنها معنادار بوده است (P value <0.0001). با توجه به اینکه mean Diff منفی شده است، بنابراین این اختلاف به سمت کمتر بودن میانگین در گروه Control تعبیر میشود.
با این حال وقتی مقایسه ما بین دو گروه Control و Treated+Antagonist انجام میشود، بیانگر عدم اختلاف معنادار بین این دو گروه است (P value = 0.8274).
بررسی بین Treated و Treated+Antagonist نشان میدهد اختلاف بین این دو معنادار است (P value = 0.0002). در این حالت mean Diff مثبت است، به معنای آنکه اختلاف معنادار به سمت بیشتر بودن Treated نسبت به Treated+Antagonist است.
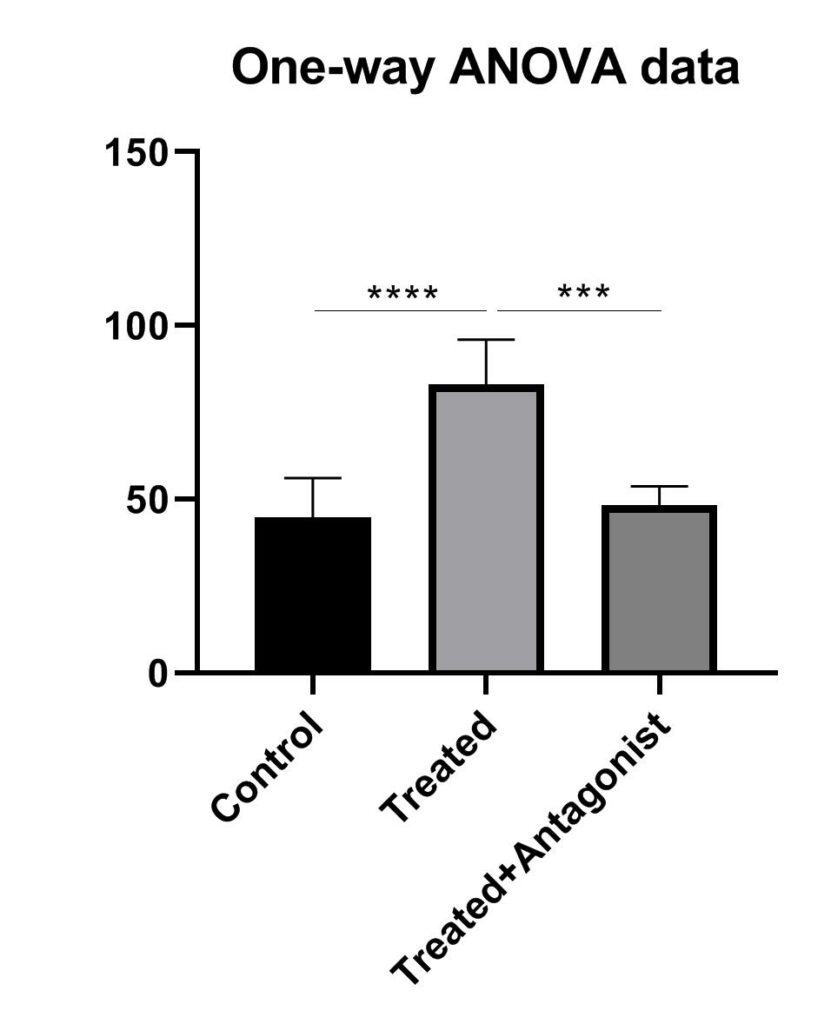
این موارد را میتوانیم به صورت یک نمودار ساده در شکل زیر نشان دهیم.
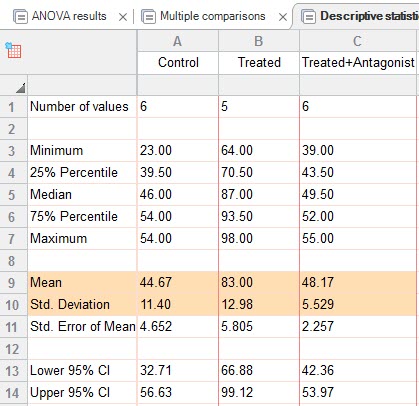
آنچه که در نهایت باقی میماند، مشاهده آمارههای توصیفی به دست آمده برای هر کدام از گروههای Treated ،Control و Treated+Antagonist است. این مطلب را میتوانیم در زبانه Descriptive statistics ببینیم.
میانگین، انحراف معیار و سایر آمارههای توصیفی برای هر ستون در جدول بالا آمده است.
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2020). Educational example Ordinary one-way ANOVA GraphPad Prism Software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/ordinary-one-way-anova/.php
For example, if you viewed this guide on 12th January 2022, you would use the following reference
GraphPad Statistics (2020). Educational example Ordinary one-way ANOVA GraphPad Prism Software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/ordinary-one-way-anova/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.