یافتن نقاط تاثیرگذار یا داده‌های موثر Influence Statistics در تحلیل رگرسیونی

توضیحات داده‌های موثر Influence Data برگرفته شده از کتاب روش های پیشرفته آماری و کاربردهای آن

 

داده‌های موثر هنگامی که در یک مدل رگرسیونی وارد می‌شوند تاثیری شدید بر روی ضرایب رگرسیونی خواهند داشت به نحوی‌که اگر آن‌ها را از معادله رگرسیونی کنار بگذاریم نتایج حاصل از برازش ضرایب رگرسیونی متحول خواهد شد. این وضعیت، در فرایند برازش مدل بر داده‌ها مطلوب نیست زیرا ما به دنبال یافتن مدلی هستیم که به اندازه‌ی عددی تعداد کمی از مشاهدات حساس نباشد و تمام نقاط کم و بیش به طور یکسان بر روی مدل اثرگذار باشند.

به عنوان مثال به داده‌های فایل Influence Statistics توجه کنید. فایل دیتای این مثال را می‌توانید از اینجا دریافت کنید. داده‌های این فایل مربوط به متوسط سن زنان در زمان ازدواج و میانگین تعداد فرزندان آن‌ها در 15 استان کشور می‌باشد. در شکل زیر نمودار پراکنش میان این دو کمیت رسم شده است. این کار با استفاده از نرم‌افزار SPSS انجام شده است.

 

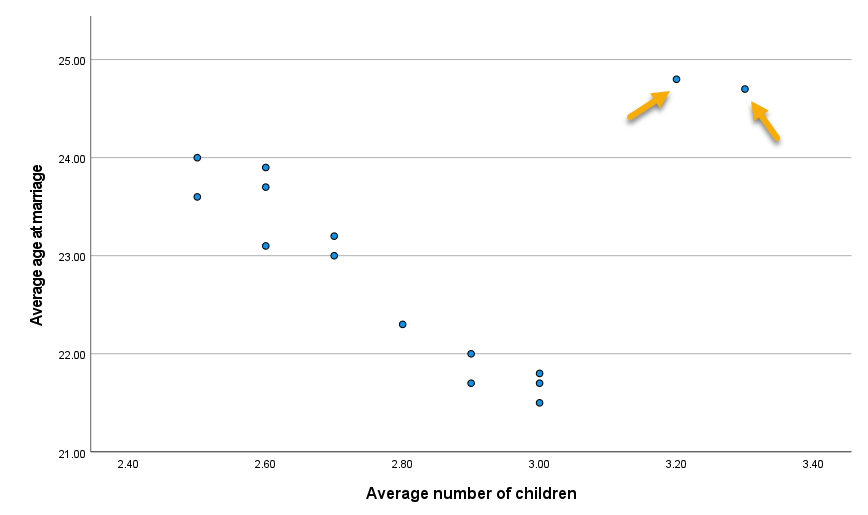
در دو استان، مشاهدات به دست آمده متفاوت از سایر استان‌ها می‌باشد. نتایج آن‌ها در بالا سمت راست دیده می‌شود. ما در این مثال به دنبال یافتن یک معادله رگرسیونی و ارتباط این دو کمیت با یکدیگر هستیم. سوال ما در این پژوهش این است که آیا هر چه میانگین سن ازدواج افزایش یافته، تعداد فرزندان کمتر شده است؟ در شکل زیر خط رگرسیون بدون وجود این دو استان و با در نظر گرفتن این دو استان به دست آمده است. این کار با استفاده از نرم‌افزار Minitab انجام شده است.

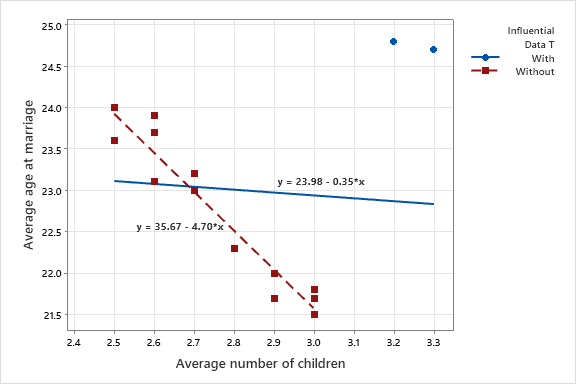
همان‌گونه که مشاهده می‌شود وجود این دو استان توانسته است خط رگرسیونی آبی رنگ را به سمت خود متمایل کند. به وضوح وجود دو مشاهده به عنوان داده‌های موثر، خط رگرسیونی را به سمت بالا متمایل کرده‌ است.

خط رگرسیونی قرمز رنگ که بدون در نظر گرفتن این دو استان به سایر داده‌ها برازش داده شده است، به خوبی توانسته است از بین نقاط بگذرد.

استفاده از تحلیل رگرسیون خطی نشان می‌دهد که اندازه ضریب زاویه و یا همان شیب خط و ضریب $ \displaystyle {{b}_{1}}$ برای خط شامل دو استان موثر، برابر با 0.347- و برای خط بدون این دو استان برابر با 4.699- به دست می‌آید که کاملاً با یکدیگر اختلاف دارند. در واقع معادلات رگرسیونی به صورت زیر خواهند بود.

$ \displaystyle \begin{array}{l}With\begin{array}{*{20}{c}} : & {} \end{array}\hat{y}=23.98-0.347x\\Without\begin{array}{*{20}{c}} : & {} \end{array}\hat{y}=35.67-4.699x\end{array}$

که در آن $ \displaystyle {\hat{y}}$ مقدار برازش شده برای متوسط سن زنان در زمان ازدواج و x میانگین تعداد فرزندان آن‌ها می‌باشد.

موضوعی که در این متن به آن می‌پردازیم این است که ما می‌توانیم یک یافته‌ی مهم دیگر نیز که به ما در درک و شناخت داده‌های موثر، مفید است به دست بیاوریم. با استفاده از نرم‌افزار می‌توانیم اندازه‌ی عوض شدن عرض از مبداء $ \displaystyle {{b}_{0}}$ و ضریب زاویه خط رگرسیون $ \displaystyle {{b}_{1}}$، به ازای حذف هر یک از مشاهدات را بیابیم. به معنای آن‌که دریابیم با حذف هر کدام از مشاهدات، اندازه‌ی عرض از مبداء و ضریب زاویه چقدر عوض می‌شود. با استفاده از این روش می‌توانیم داده‌های موثر Influence Data مدل رگرسیونی را به دست بیاوریم.

جهت انجام تحلیل رگرسیون خطی و البته بعد از آن به دست آوردن آماره‌های موثر Influence Statistics، از مسیر زیر در نرم‌افزار SPSS استفاده می‌کنیم.

Analyze → Regression → Linear

 

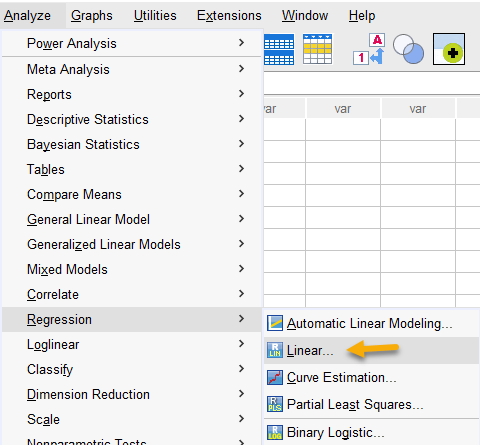
با رفتن به این مسیر، پنجره زیر با نام Linear Regression برای ما باز می‌شود. ما Age را در بخش Dependent و Children را در بخش Block یا Independent قرار می‌دهیم.

 

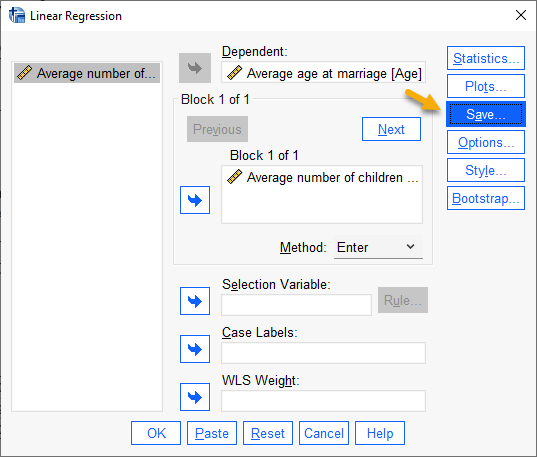
با استفاده از تب Save در این پنجره، می‌توانیم به یافتن اطلاعات و یافته‌هایی درباره‌ی آماره‌های موثر مطالعه دست پیدا کنیم.

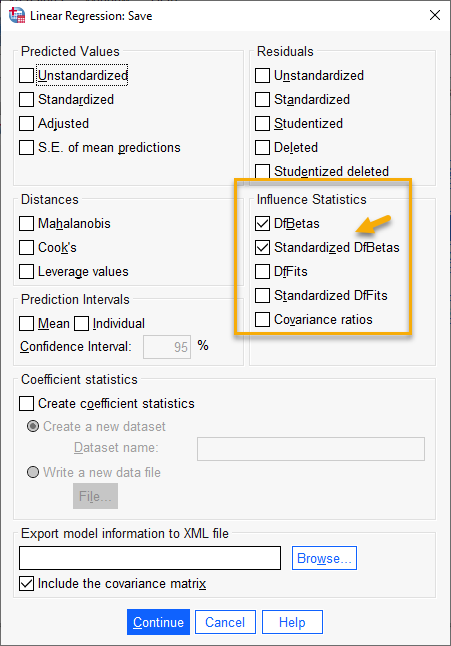
همان‌گونه که بیان کردیم، هدف ما در این متن به دست آوردن اطلاعات و یافته‌هایی درباره‌ی آماره‌های موثر مطالعه است. جهت انجام این کار در پنجره Linear Regression بر روی گزینه Save می‌زنیم و وارد پنجره Linear Regression Save می‌شویم.

 

در این پنجره کادری با نام Influence Statistics دیده می‌شود. گزینه DfBetas را انتخاب می‌کنیم.

با انتخاب این گزینه و انجام تحلیل رگرسیونی در فایل داده‌ها دو ستون داده به نام‌های DFB0_1 و DFB1_1 ایجاد می‌شود. داده‌های ستون DFB0_1 برای هر استان اندازه دگرگونی در عرض از مبداء به ازای حذف آن استان از مدل رگرسیونی و DFB1_1 اندازه دگرگونی در ضریب زاویه خط رگرسیونی به ازای حذف آن استان از مدل رگرسیونی را نشان می‌دهد.

بنابراین با استفاده از این روش قادر خواهیم بود که دریابیم، حذف هر کدام از استان‌ها، تا چه اندازه می‌تواند ضرایب مدل رگرسیونی یعنی $ \displaystyle {{b}_{0}}$ و $ \displaystyle {{b}_{1}}$، را کم یا زیاد کند.

هنگامی که در این پنجره Continue و سپس OK می‌کنیم، در فایل دیتا می‌توانیم ستون‌های جدید DFB0_1 و DFB1_1 را مشاهده کنیم. تصویر زیر را ببینید.

 

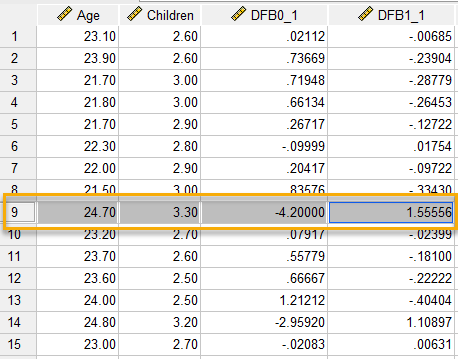
همان‌گونه که در تصویر بالا مشاهده می‌کنید، دو ستون جدید به نام‌های DFB0_1 و DFB1_1 به دیتا اضافه شده است. به عنوان مثال به سطر نهم نگاه کنید. DFB0_1 برای این سطر 4.2- و DFB1_1 برای این سطر 1.56 شده است. این یافته نشان می‌دهد که اگر سطر نهم را از این داده‌ها حذف کنیم و سپس با داده‌های باقیمانده یک مدل رگرسیونی جدید بر داده‌ها برازش دهیم، $ \displaystyle {{b}_{0}}$ و $ \displaystyle {{b}_{1}}$، این مدل جدید به ترتیب 4.2- و 1.56 واحد کاهش خواهد یافت.

در معادلات زیر می‌توانید، مدل رگرسیونی با بودن سطر نهم و بدون سطر نهم را مشاهده کنید.

$ \displaystyle \begin{array}{l}With\begin{array}{*{20}{c}} {} & {\left( {Row9} \right)} \end{array}\begin{array}{*{20}{c}} : & {} \end{array}\hat{y}=23.98-0.347x\\Without\begin{array}{*{20}{c}} {} & {\left( {Row9} \right)} \end{array}\begin{array}{*{20}{c}} : & {} \end{array}\hat{y}=28.179-1.903x\end{array}$

همان‌گونه که در معادلات بالا می‌بینید، ضریب ثابت مدل وقتی سطر نهم در مدل وجود دارد، برابر با 23.98 است. اما وقتی این سطر از دیتا حذف شود، ضریب ثابت برابر با 28.179 خواهد بود. بنابراین اختلاف آن‌ها برابر با 4.2- = 28.18 – 23.98 است.

به همین ترتیب ضریب رگرسیونی مدل وقتی سطر نهم در مدل وجود دارد، برابر با 0.347- است. اما وقتی این سطر از دیتا حذف شود، ضریب ثابت برابر با 1.903- خواهد بود. بنابراین اختلاف آن‌ها برابر با 1.56 = (1.903-) – 0.347- است.

یافتن نقاطی که تاثیر زیادی بر روی مدل رگرسیونی دارند توجه به این مقادیر و استاندارد شده‌ی آن‌ها است. به منظور یافتن اندازه‌های استاندارد شده‌ی این مقادیر در کادر Influence Statistics گزینه‌ی Standardized DfBetas را انتخاب کنید.

 

با انتخاب گزینه Standardized DfBetas، دو ستون جدید دیگر با نام‌های SDB0_1 و SDB1_1 در فایل دیتا ایجاد می‌شود. تصویر زیر را ببینید.

 

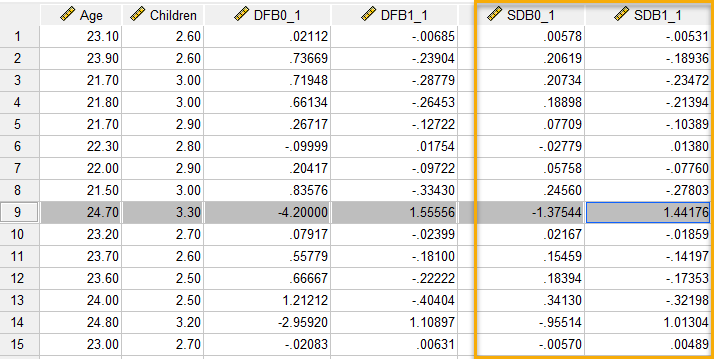
در استان‌هایی که اندازه دگرگونی‌های استاندارد شده‌ی آن بزرگ است، نتیجه می‌شود که حذف آن استان از مدل رگرسیونی اختلاف زیادی در ضرایب  $ \displaystyle {{b}_{0}}$ و $ \displaystyle {{b}_{1}}$، ایجاد می‌کند، لذا آن استان به عنوان یک داده‌ی موثر شناخته می‌شود. معمولاً مشاهداتی که اختلاف SDB0_1 و SDB1_1 آن‌ها بزرگتر از $ \displaystyle \frac{2}{{\sqrt{n}}}$ است (در این مثال $ \displaystyle \frac{2}{{\sqrt{{15}}}}=0.5164$)، داده‌ی موثر نامیده می‌شوند.

همان‌گونه که مشاهده می‌کنید در استان‌های شماره 9 و 14 اختلاف مقادیر $ \displaystyle {{b}_{0}}$ و $ \displaystyle {{b}_{1}}$ آن‌ها در اثر حذف هر یک از این دو استان در مدل رگرسیون از عدد 0.516 بزرگتر هستند و لذا این دو استان به عنوان داده‌های موثر در مطالعه شناخته می‌شوند.

سوال   سوال مهمی که در این مطرح می‌شود این است که اگر مشاهداتی را که بر روی نتایج تاثیر زیادی دارند و اصطلاحاً به آن‌ها داده‌ی موثر می‌گویند، یافتیم چه باید کنیم؟ پاسخ این است است که در ابتدا مطمئن شوید که این داده‌ها ناشی از خطاهای جمع‌آوری داده‌ها و ورود داده‌ها به نرم‌افزار نمی‌باشد. اگر چنین خطایی وجود دارد آن را اصلاح کنید. چنانچه مقدار مشاهدات صحیح بود، بررسی کنید آیا غیر معمول بودن نمونه مورد نظر تاثیری بر روی خط رگرسیون دارد. به عنوان مثال هنگامی که رابطه بین سن ازدواج و تعداد فرزندان را بررسی می‌کنید، ممکن است مواردی را بیابید که اندازه‌های عددی هر دو کمیت در آن‌ها بزرگ است. در این حالت یک توضیح ممکن است این باشد که با وجود این‌که دختران این استان دیر ازدواج می‌کنند اما ویژگی‌های باروری زنان این استان و یا رسومات اجتماعی خانوار‌های این استان تعداد فرزندان زیاد را می‌طلبد.

در این حالت می‌توانید مدل‌های رگرسیون جداگانه‌ای برای استان‌هایی که دارای این ویژگی و آن‌هایی که فاقد این ویژگی هستند، تشکیل دهید. یک راه‌حل دیگر آن است که نتایج آماری خود را در دو بخش یعنی با در نظر گرفتن داده‌های موثر و بدون در نظر گرفتن آن‌ها، ارایه دهید. کاری که نباید انجام دهید آن است که به طور اختیاری و بدون هیچ‌گونه توجیه علمی و منطقی این نقاط را به هر طریقی از مدل و مطالعه خود خارج کنید. به این نکته توجه کنید که داده‌های موثر بخشی از فرایند تحقیق شما و از جمله داده‌های واقعی تحقیق می‌باشد که به هیچ‌وجه نباید آن‌ها را حذف کرد.

 

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2022). Effective Influence Statistics data in regression analysis. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/influence-statistics/.php

For example, if you viewed this guide on 12^th January 2022, you would use the following reference

GraphPad Statistics (2022). Effective Influence Statistics data in regression analysis. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/influence-statistics/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.