رگرسیون خطی چندگانه سلسله مراتبی Hierarchical Multiple Linear Regression

 Hierarchical Multiple Linear Regression 

این تحلیل معمولاً به منظور کنترل آماری کمیت‌های خاص انجام می‌شود، تا ببینیم که آیا افزودن Variableها به چه اندازه توانایی مدل جهت پیش‌بینی درست را بهبود می‌بخشد. همچنین هدف دیگر ما از این تحلیل آماری، بررسی اثر تعدیل کننده یک یا چند کمیت دیگر است. به معنای این‌که آیا ورود یک یا چند Variable جدید در مدل، بر رابطه بین کمیت‌های مستقل و وابسته یعنی DV و IVها اثر می‌گذارد و یا فاقد اثرگزاری است.

رگرسیون سلسله مراتبی راهی است برای نشان دادن اینکه آیا کمیت‌های مورد علاقه شما پس از قرار گرفتن سایر کمیت‌ها در مدل، مقدار قابل توجهی از واریانس کمیت وابسته وابسته (منظور همان R Square است) را توضیح می‌دهند یا خیر. در این روش، چندین مدل رگرسیون را با اضافه کردن کمیت‌هایی به مدل قبلی در هر مرحله می‌سازید. مدل‌های بعدی همیشه شامل مدل‌های کوچکتر در مراحل قبلی می‌شوند. در بسیاری از موارد، هدف ما این است که تعیین کنیم آیا کمیت‌های جدید اضافه شده، بهبود قابل توجهی در R Square یعنی نسبت واریانس توضیح داده شده در DV توسط مدل رگرسیونی، نشان می‌دهند یا خیر.

به عنوان مثال، ممکن است بخواهید بدانید که آیا سن دانشجویان و تعداد ساعت‌های مطالعه با معدل آنها مرتبط است یا خیر. در اینجا می‌توانید از یک تحلیل رگرسیون خطی چندگانه با نام اختصاری (MLR) استفاده کنید تا ببینید آیا این کمیت‌ها (سن و ساعات مطالعه) معدل افراد را پیش‌بینی می‌کنند یا خیر. یعنی رابطه رگرسیونی زیر را به دست بیاورید.

Score =  b₀ + b₁ Age + b₂ Study hours

با این حال، اگر فکر می‌کنید که رابطه بین تعداد ساعات مطالعه و معدل برای دانشجویان جوان‌تر از دانشجویان مسن‌تر، قوی‌تر است، در این حالت می‌توانید از رگرسیون خطی سلسله مراتبی استفاده کنید.

ما در این متن با استفاده از نرم‌افزار SPSS به آموزش این مطلب خواهیم پرداخت. در این نرم‌افزار، مدل رگرسیون خطی سلسله مراتبی، با استفاده از ابزاری به نام Block اجرا می‌شود. از طریق این ابزار قادر خواهیم بود یک مدل رگرسیونی را که در آن مجموعه‌ای از پیش‌بینی کننده‌ها وجود دارد، در بلوک‌ها یا مراحل مختلف وارد مدل کنیم و سپس آزمایش کنم که آیا اضافه کردن هر بلوک، مدل را نسبت به بلوک‌های قبلی بهبود بخشیده است یا خیر. در ادامه درباره روش انجام کار و مسیر نرم‌افزار صحبت خواهیم کرد.

در مثال بالا، معدل Dependent Variable (DV) ما خواهد بود. بلوک اول، فقط دو کمیت پیش‌بینی‌کننده را شامل می‌شود (سن و ساعات مطالعه)، در بلوک بعدی کمیتی را اضافه می‌کنید که نشان‌دهنده تعامل و اثر متقابل بین سن و ساعات مطالعه به عنوان کمیت پیش‌بینی کننده سوم است. یعنی مدل زیر را به دست می‌آورید.

Score =  b₀ + b₁ Age + b₂ Study hour + b₃ Age * Study hours

اگر عبارت تعاملی (سن × ساعات مطالعه) از نظر آماری معنادار باشد و مدل را بهتر برازش کند (مثلاً R Square بالاتری داشته باشد) در این صورت می‌توانید نتیجه بگیرید که یک اثر تعدیل Moderation Effect وجود دارد.

مثال رگرسیون سلسله مراتبی

 Hierarchical Regression Example 

 در یک مطالعه بر روی 150 نفر شاخص‌های قلبی و عروقی افراد شامل crp ،chol و sbp اندازه‌گیری شده است. همچنین ما وزن افراد همراه با جنسیت و میزان فعالیت ورزشی و بدنی آن‌ها در طول شبانه روز را به دست آورده‌ایم. هدف ما در این مطالعه به دست آوردن ارتباط بین این Variable ها با شاخصی به نام Score است. در واقع در این مطالعه Score به عنوان Dependent Variable (DV) و کمیت‌های crp ،chol و sbp همراه با Gender ،Weight و Activity کمیت‌های مستقل Independent Variable (IV) را تشکیل می‌دهند.

فایل دیتای این مثال را می‌توانید از اینجا دریافت کنید. در تصویر زیر بخشی از داده‌های این مثال را مشاهده می‌کنید.

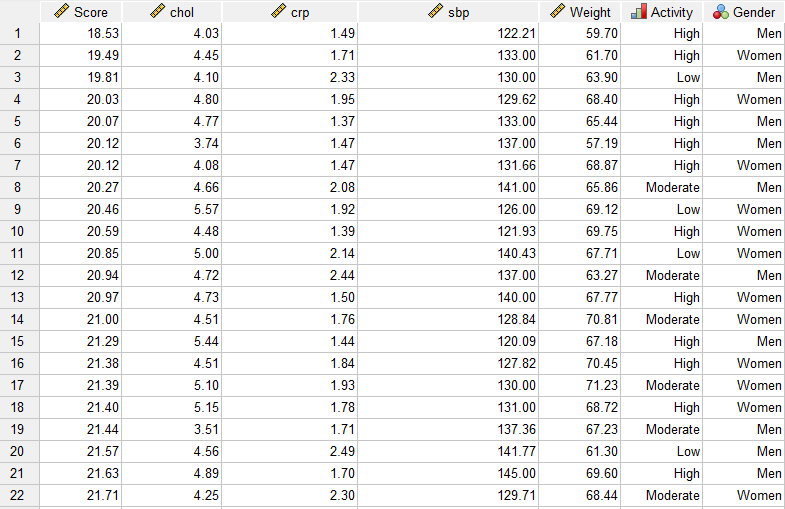
همان‌گونه که بیان کردیم در این مثال به دنبال این هستیم که ارتباط بین DV و IVها را به دست بیاوریم. این کار بهتر است در قالب یک مدل رگرسیونی خطی چندگانه که به اختصار آن را MLR می‌گوییم انجام شود. همچنین ما در پی این هستیم که تحلیل رگرسیونی خود را به صورت سلسله مراتبی Hierarchical انجام دهیم. یعنی یک مدل HMLR داشته باشیم.

با انجام این کار می‌توانیم کمیت‌های مستقل خود را نه به صورت یکجا و یک دفعه بلکه در قالب Block های مختلف وارد مدل کنیم. این کار سبب می‌شود بتوانیم نقش و جایگاه هر IV را در مدل به دست بیاوریم. همچنین می‌توانیم بررسی کنیم آیا کمیت‌ها و Variableهای دیگری نیز بر مدل اثر گزار است یا خیر، به عبارتی آیا اثر تعدیل‌کننده Moderating Effect وجود دارد یا نه.

در واقع هدف ما طراحی یک مدل رگرسیون خطی چندگانه، آن هم در چند گام و به صورت سلسله مراتبی است. هر کدام از آن‌ها را در ادامه بیان می‌کنیم.

در ابتدا می‌خواهیم مدل رگرسیون چندگانه شامل Score به عنوان کمیت وابسته و شاخص‌های قلبی و عروقی یعنی crp ،chol و sbp به عنوان کمیت‌های مستقل و اثرگزار بر Score را مورد بررسی قرار دهیم. در واقع به دنبال این هستیم که مدل رگرسیونی زیر را برازش دهیم.

Score =  b₀ + b₁ chol + b₂ crp + b₃ sbp

بر مبنای این مدل می‌خواهیم به دست بیاوریم کدام شاخص‌ها احیاناً بر Score اثرگزار معنادار است و ضریب تعیین مدل یا همان R Square چقدر است.

   در مرحله‌ی بعد می‌خواهیم اثر کمیت Weight را به عنوان تعدیل کننده Moderator مورد بررسی قرار دهیم. هدف ما این است که دریابیم آیا وزن می‌تواند به عنوان یک مداخله کننده، روی مدل رگرسیونی چندگانه شامل Score و شاخص‌های crp ،chol و sbp. اثرگزار باشد یا خیر. ورود Weight به مدل رگرسیونی تا چه اندازه می‌تواند R Square مدل را افزایش دهد. در واقع به دنبال این هستیم که مدل رگرسیونی زیر را برازش دهیم.

 Score =  b₀ + b₁ chol + b₂ crp + b₃ sbp + b₄ weight

نکته در ابتدا به این نکته دقت کنید که همواره مدل‌های مرتبه بالاتر شامل مدل‌های مرتبه پایین‌تر نیز می‌شوند. به عبارت ساده مدل گام دو همان مدل گام یک است که به آن Weight نیز اضافه شده است.

   ما در این مطالعه Variableهای دیگری نیز به نام جنسیت و فعالیت بدنی داریم. علاقمند هستیم در گام سوم مدل رگرسیون سلسله مراتبی خود، Variableهای Gender و Activity را نیز به عنوان تعدیل کننده‌های دیگر مورد بررسی قرار دهیم. هدف ما در این مرحله این است که بفهمیم جنسیت و فعالیت به عنوان مداخله کننده‌ها، آیا می‌توانند بر روی مدل رگرسیونی چندگانه شامل Score و شاخص‌های crp ،chol و sbp. هنگامی که وزن نیز به عنوان تعدیل کننده وارد مدل شده است، اثرگزار باشند یا خیر. همچنین میزان افزایش R Square مدل هنگام ورود جنسیت و فعالیت به مدل رگرسیونی را ارزیابی کنیم. به این ترتیب ما مدل رگرسیونی زیر را برازش می‌دهیم.

 Score =  b₀ + b₁ chol + b₂ crp + b₃ sbp + b₄ weight + b₅ Gender + b₆ Activity

حال در ادامه ما به دنبال طراحی و ساختن مدل رگرسیونی خطی چندگانه سلسله مراتبی HMLR که در بالا آن را توصیف کردیم، می‌باشیم.

طراحی مدل رگرسیونی سلسله مراتبی

 Designing a hierarchical regression model 

جهت طراحی و ساختن مدل HMLR که در بالا مراحل تئوری و اجرای آن را گام به گام نوشتیم، از مسیر زیر در نرم‌افزار SPSS استفاده می‌کنیم.

Analyze → Regression → Linear

با رفتن به این مسیر، پنجره زیر با نام Linear Regression برای ما باز می‌شود.

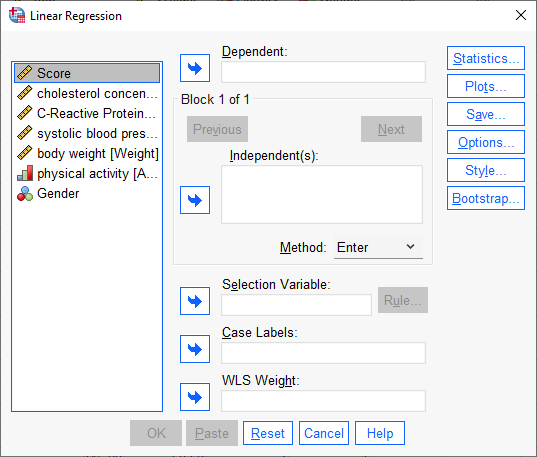
ما در اینجا می‌خواهیم به طراحی مدل رگرسیون سلسله مراتبی، همان‌گونه که در گام‌های 1، 2 و 3 بالا توضیح دادیم، بپردازیم. برای انجام این کار، مراحل زیر را پی می‌گیریم.

خب خیلی ساده، همان‌طور که بارها بیان کردیم Score به عنوان Dependent و کمیت وابسته در این مطالعه قرار دارد. بنابراین آن را در کادر Dependent قرار می‌دهیم.

گفتیم که می‌خواهیم در سه گام، رگرسیون سلسله مراتبی طراحی کنیم. به ازای هر گام باید یک بلوک Block داشته باشیم. بنابراین در نرم‌افزار SPSS آن‌ها را به ترتیب می‌سازیم.

در اینجا مدل 1 رگرسیونی خود را می‌سازیم. Independentها همان شاخص‌های crp ،chol و sbp هستند. بنابراین آن‌ها را به کادر Independent(s) انتقال می‌دهیم. تصویر زیر را ببینید.

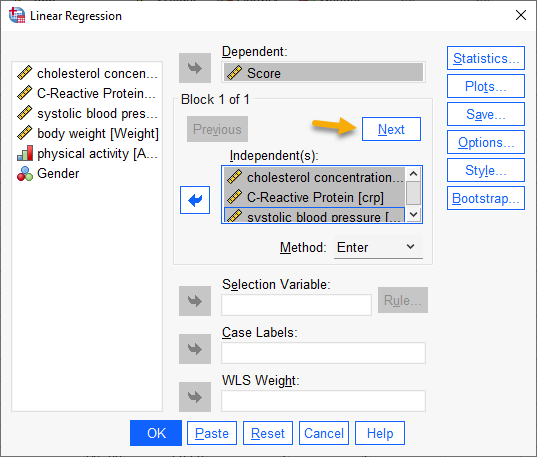
با انجام این کار گام و بلوک 1 مدل رگرسیون سلسله مراتبی برای ما ساخته می‌شود. همان‌گونه که بالاتر گفتیم، این مدل به صورت زیر است.

Score =  b₀ + b₁ chol + b₂ crp + b₃ sbp

حال باید گام 2 و بلوک 2 را در مدل سلسله مراتبی طراحی کنیم. برای انجام این کار، در همان بلوک 1 بر روی تب Next که با قرار گرفتن Independentها فعال شده است، کلیک کنید. با انجام این کار به پنجره زیر می‌روید.

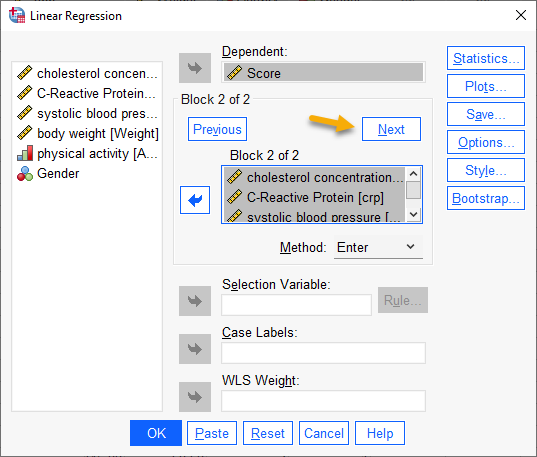
در این بلوک علاوه بر کمیت‌های مستقل مدل قبلی یعنی شاخص‌های crp ،chol و sbp، کمیت مستقل دیگر مدل 2 یعنی Weight نیز قرار می‌گیرد. همان‌گونه که بالاتر گفتیم هدف ما این است که بررسی کنیم آیا وزن می‌تواند به عنوان یک تعدیل کننده Moderator در مدل قرار گیرد یا خیر؟ ما در این بلوک مدل زیر را برازش می‌دهیم.

 Score =  b₀ + b₁ chol + b₂ crp + b₃ sbp + b₄ weight

حال باید گام 3 و بلوک 3 را در مدل سلسله مراتبی طراحی کنیم. برای انجام این کار، در بلوک 2 بر روی تب Next کلیک کنید. با انجام این کار به پنجره زیر می‌روید.

در این بلوک علاوه بر کمیت‌های مستقل مدل قبلی یعنی شاخص‌های crp ،chol و sbp، همراه با Moderator وزن، کمیت مستقل دیگر مدل 3 یعنی Gender و Activity نیز در بلوک 3 قرار می‌گیرد. ما در این مدل می‌خواهیم بررسی کنیم آیا جنسیت و فعالیت بدنی می‌توانند به عنوان تعدیل کننده‌ها در مدل قرار گیرند یا خیر؟ ما در این بلوک مدل زیر را برازش می‌دهیم.

 Score =  b₀ + b₁ chol + b₂ crp + b₃ sbp + b₄ weight + b₅ Gender + b₆ Activity

نکته هنگامی که در حال انجام رگرسیون سلسله مراتبی هستید، دقت کنید که در پنجره Linear Regression، بخش Method بر روی گزینه Enter قرار گرفته باشد.

خب، حال OK کنید تا بتوانیم نتایج و خروجی‌های نرم‌افزار را مشاهده کنیم. البته ما می‌توانستیم با استفاده از انواع تب‌ها و منوهایی که در پنجره رگرسیون خطی وجود دارد، نتایج بیشتری هم به دست بیاوریم. مثلاً فواصل اطمینان برای ضرایب رگرسیونی، آماره دوربین واتسن Durbin-Watson، آماره‌های توصیفی، ماتریس کوواریانس و یا پلات‌هایی مانند Normal Probability Plot و یا انواع گراف‌های مربوط به باقیمانده‌ها. با این حال در این متن کاری به آن‌ها نداریم و بیشتر می‌خواهیم بر روی رگرسیون سلسله مراتبی تمرکز کنیم.

خروجی‌ها و نتایج نرم‌افزار

 Output 

هنگامی که OK می‌کنیم، در پنجره Output نرم‌افزار SPSS، نتایج و جدول‌های زیر به دست می‌آید. ما در ادامه به تفکیک هر کدام از آن‌ها را توضیح می‌دهیم.

در ابتدای نتایج جدول Variables Entered/Removed دیده می‌شود. این جدول به بیان کمیت‌ها و Variableهای مستقل موجود در مدل و اضافه شده در هر گام و بلوک می‌پردازد.

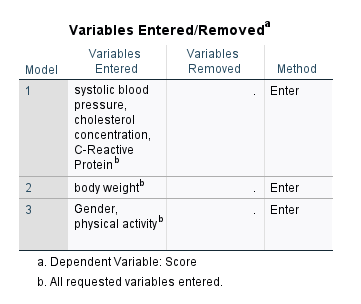
همان‌گونه که در جدول بالا دیده می‌شود، سه مدل در این مثال طراحی شده است. اینها همان بلوک‌های ما هستند که در تنظیمات پنجره Linear Regression آن‌ها را ساختیم.

• در مدل 1، Variableهای crp ،chol و sbp به مدل اضافه شده‌اند.
• در مدل 2، علاوه بر Variableهای موجود در مدل 1، Weight نیز به مدل رگرسیونی اضافه شده است.
• در مدل 3، علاوه بر Variableهای موجود در مدل 2، Gender و Activity نیز به مدل اضافه شده است.

جدول بعدی با نام Model Summary شامل همان چیزی است که در این متن، چندین بار به ان اشاره کردیم و آن R Square یا ضریب تعیین است. با استفاده از این آماره می‌توانیم دریابیم مدل رگرسیون با استفاده از IVهای خود به چه اندازه می‌تواند واریانس و پراکندگی DV را بیان کند. هر چقدر این عدد (که بین صفر و یک قرار دارد) به عدد یک نزدیکتر باشد، نشان‌دهنده بهتر بودن مدل رگرسیونی برازش شده است.

در جدول Model Summary بالا، R Square هر سه بلوک مربوط به مدل‌های رگرسیونی آمده است. R Square برای مدل 1 برابر با 0.298 شده است. با این حال عدد آن برای مدل 2 به شدت بالاتر و برابر با 0.591 است. اندازه اختلاف و در واقع بهبود مدل رگرسیونی 2 نسبت به 1، عدد بالایی است. رابطه زیر را ببینید.

Δ (1) = R Square (2) – R Square (1) = 0.591 – 0.298 = 0.293

این رابطه به معنای آن است که مدل 2 نسبت به مدل 1 به اندازه 0.293 واحد، بهبود پیدا کرده است. این بهبود عملکرد نتیجه اضافه شدن Weight به بلوک 2 در مدل رگرسیونی است. بنابراین تا اینجا به نظر می‌رسد وزن دارای یک اثرگزاری قوی بر Dependent است و می‌توان آن را یک تعدیل کننده یا میانجی Moderator در مدل رگرسیونی بین Score و شاخص‌های قلبی و عروقی در نظر گرفت. به این معنا که وزن افراد می‌تواند بر رابطه بین DV و IVها اثرگزار باشد.

در جدول Model Summary بالا، R Square برای مدل 3 برابر با 0.685 شده است. این عدد نشان می‌دهد اضافه شدن جنسیت و فعالیت بدنی می‌تواند مدل 2 را به اندازه 0.094 واحد بهبود دهد. رابطه زیر را ببینید.

Δ (2) = R Square (3) – R Square (2) = 0.685 – 0.591 = 0.094

این میزان اضافه شدن R Square در مدل 3 (یعنی 0.094 واحد) که در نتیجه وارد شدن Gender و Activity به بلوک 3 ایجاد شده است را در ادامه بیشتر بررسی خواهیم کرد.

نکته یک نکته واضح و تقریباً بدیهی در مدل‌های رگرسیونی این است که اضافه شدن یک یا چند X (که نام آن را Independent Variable می‌نامیم) به مدل رگسیونی، R Square را بالا می‌برد. در واقع رابطه و فرمول R Square که به صورت نسبت واریانس توضیح داده شده توسط مدل به واریانس کمیت وابسته تعریف می‌شود، به گونه‌ای است که مخرج کسر همواره ثابت است اما صورت کسر با اضافه شدن X ها افزایش می‌یابد. بنابراین در هر صورت وارد شدن Xهای با ربط یا بی‌ربط به مدل رگرسیونی به هر حال و در هر صورت R Square را افزایش می‌دهند. آن‌چه که برای ما اهمیت دارد، میزان و اندازه اضافه شدن R Square هنگام ورود X های جدید به مدل رگرسیونی است.

در نتایج مدل رگرسیون خطی، جدول آنالیز واریانس یا همان ANOVA وجود دارد. همان‌گونه که می‌دانیم نتایج این جدول به معنادار بودم مدل رگرسیونی برازش شده و ضرایب رگرسیونی به صورت کلی می‌پردازد. در ادامه نتایج این جدول بیان شده است. از آن‌جا که ما در حال کار بر روی یک مدل سلسله مراتبی با سه بلوک هستیم، بنابراین به ازای هر کدام از آن‌ها، جدول ANOVA جداگانه آمده است.

نتایج جدول بالا بیانگر معنادار بودن هر سه بلوک رگرسیونی است (P value < 0.001). این مطلب نشان می‌دهد هر سه مدل رگرسیونی برازش شده، مناسب بوده و ضرایب رگرسیونی آن‌ها حداقل در یک مورد معنادار است. جهت فهم بهتر و دقیق‌تر ضرایب رگرسیونی و بررسی جداگانه هر کدام از Independent Variable ها، جدول ضرایب رگرسیونی زیر را ببینید.

در جدول زیر با نام Coefficients ضرایب رگرسیونی به ازای هر کدام از مدل‌ها و بلوک‌ها آمده است. در ادامه بیشتر آن را توضیح می‌دهیم.

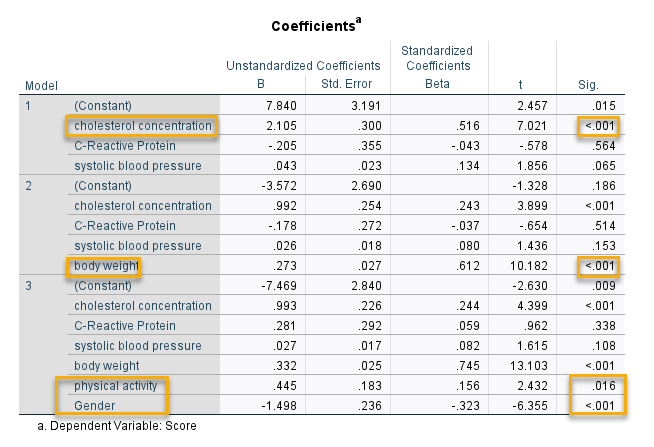
مدل 1. در مدل 1، chol معنادار و مثبت گزارش شده است. IV های دیگر یعنی crp و sbp در سطح پنج درصد معنادار به دست نیامدند. این مطلب نشان می‌دهد فقط chol دارای تاثیر مستقیم و معنادار بر Score است. معنادار شدن مدل رگرسیونی 1 در جدول ANOVA به دلیل معنادار شدن همین chol به دست آمده است. خاطرتان باشد بیان کردیم که R Square مدل در اینجا برابر با 0.298 (نزدیک به 30 درصد) است.

مدل 2. در مدل 2 که شامل همان Variable های مدل 1 به اضافه weight است، همچنان chol معنادار است. نکته با اهمیت این است که وزن نیز کاملاً معنادار و دارای ارتباط قوی و مثبا با Score به دست آمده است. ضریب رگرسیونی استاندارد شده آن برابر با 0.612 واحد است. قبلاً نشان دادیم که R Square این مدل برابر با 0.591 (حدود 59 درصد) است. این مقدار افزایش قابل توجه در R Square (0.293 واحد) به دلیل اضافه شدن یک کمیت کاملاً اثردار و معنادار (وزن) در مدل رگرسیونی است. به این ترتیب می‌توان Weight را به عنوان یک تعدیل‌کننده قوی که بر روی رابطه بین Score و شاخص‌های قلبی و عروقی اثرگزار است، شناخت و مورد بررسی قرار داد.

مدل 3. در این مدل و بخش آخر مدل رگرسیون چندگانه سلسله مراتبی، Variable های جنسیت و فعالیت بدنی اضافه شده است. R Square این مدل 0.685 (68.5 درصد) به دست آمده بود. این به معنای آن است که ورود کمیت‌های جنسیت و فعالیت بدنی توانسته است حدود 9 درصد، ضریب تعیین مدل سه را در مقایسه با مدل 2، بهبود بخشد. جدول ضرایب رگرسیونی بالا نشان می‌دهد فعالیت بدنی دارای تاثیر مثبت معنادار (P value = 0.016) و جنسیت (زنان) دارای تاثیر معنادار منفی (P value < 0.001) بر کمیت وابسته Score است. بنابراین در اینجا نیز نتیجه می‌گیریم که علاوه بر weight، جنسیت و فعالیت نیز به عنوان Moderator بر رابطه بین Score و شاخص‌های قلبی و عروقی موثر هستند.

در انتهای نتایج و خروجی‌های نرم‌افزار، جدول Excluded Variables دیده می‌شود. در این جدول کمیت‌هایی که در هر مرحله در مدل وجود ندارند و خارج شده‌اند، بیان شده است.

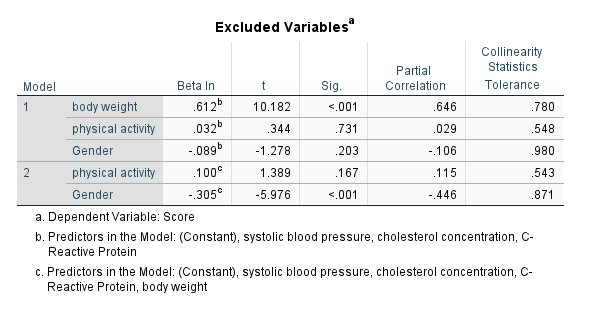
جدول Excluded Variables نشان می‌دهد در مدل 1، Variableهای وزن، جنسیت و فعالیت از مطالعه کنار رفته‌اند (البته این مطلب طبیعی است و ما در مدل 1 فقط شاخص‌های قلبی و عروقی را قرار دادیم) در مدل 2 نیز Variableهای فعالیت بدنی و جنسیت از مطالعه خارج شده‌اند. بیایید کمی درباره‌ی یافته‌های این جدول صحبت کنیم.

Beta In & t. اعداد این ستون در هر Variable مربوط به ضریب رگرسیونی استاندارد شده و آماره t مدلی هستند که از برازش Score به عنوان کمیت وابسته، شاخص‌های قلبی و عروقی به عنوان کمیت‌های مستقل و همان Variable، ایجاد می‌شود. به عنوان مثال عدد 0.032 برای Beta In و 0.344 برای t از جدول زیر به دست می‌آیند.

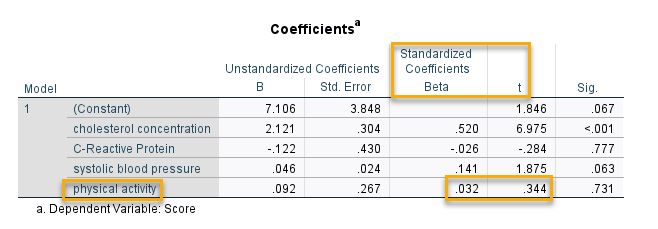
در این جدول ضرایب رگرسیونی مدلی آمده است که شامل Score به عنوان Dependent Variable و crp ،chol و sbp به عنوان Independent Variable هستند. علاوه بر آن physical activity نیز به عنوان یک Independent Variable وارد مدل شده است. ضریب رگرسیونی استاندارد شده و آماره t مربوط به physical activity همان Beta In & t جدول Excluded Variables است.

Partial Correlation. به آن ضریب همبستگی جزئی گفته می‌شود. اعدادی که در این ستون مشاهده می‌کنید، ضریب همبستگی جزئی بین آن Variable با کمیت وابسته Score است، در حالی که Independentهای مدل یعنی شاخص‌های قلبی و عروقی به عنوان کمیت‌های کنترل‌کننده قرار گرفته‌اند. به عنوان مثال عدد 0.646 مربوط به body weight صریب همبستگی جزئی بین body weight و Score را نشان می‌دهد. Sig سمت چپ آن نیز مقدار احتمال همان ضریب همبستگی جزئی است. در جدول زیر من ماتریس ضرایب همبستگی جزئی بین Score و Variableهای وزن، جنسیت و فعالیت را آورده‌ام.

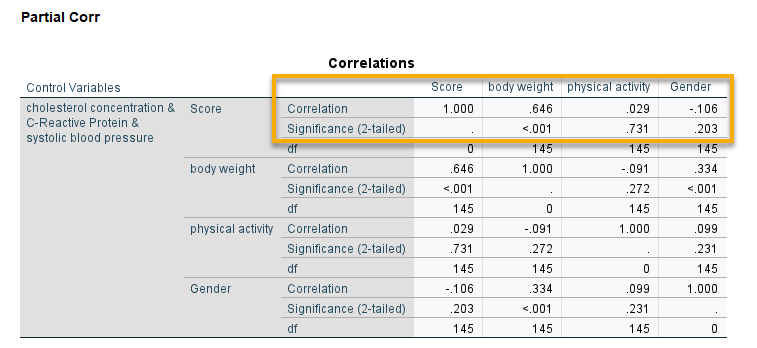
در کادری که مشخص کرده ام می‌توانید همان نتایج ستون Partial Correlation و Sig جدول Excluded Variables را ببینید.

Collinearity Statistics Tolerance. به آن هم‌خطی تطبیقی نیز گفته می‌شود. مفهوم آن‌ها جالب است. اصولاً هم خطی به بررسی وجود رابطه همبستگی بین Xهای مدل گفته می‌شود و وجود آن یک نقیصه و عیب برای مدل رگرسیونی برازش شده خواهد بود. برای فهم آن بیایید فرض کنیم می‌خواهیم بدانیم عدد 0.780 نوشته شده در ستون Collinearity Statistics Tolerance و برای body weight چیست و از کجا آمده است.

برای پاسخ بیایید یک مدل رگرسیونی بین body weight و سایر Independentهایی که همچنان در مدل حضور دارند (یعنی crp ،chol و sbp) ایجاد کنید. در این مدل، وزن به عنوان Dependent قرار می‌گیرد. حال جدول Model summary و به ویژه R Square آن را ببینید. من آن را برایتان آورده‌ام.

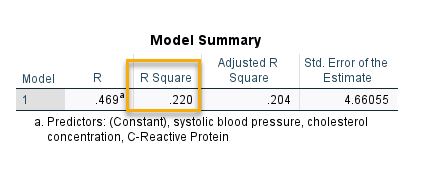
عدد R Square این مدل چقدر شده است؟ 0.220. حال عدد 0.780 بالا را که همخطی مربوط به وزن بود را ببینید. آن‌ها چه ارتباطی با هم دارند؟ 0.220 = 0.780 – 1

پاسخ این است که اعداد نوشته شده در ستون Collinearity Statistics Tolerance جدول Excluded Variables برای هر کدام از Variableها، همان یک منهای R Square مدل رگرسیونی بین آن Variable با سایر کمیت‌های موجود در مطالعه است. یعنی 0.780 همان یک منهای R Square مدل رگرسیونی بین body weight و crp ،chol و sbp است. هر چقدر این عدد به یک نزدیکتر باشد به معنای وجود همخطی ضعیف‌تر است و هر چقدر اعداد ستون Collinearity Statistics Tolerance به صفر نزدیکتر باشند به معنای وجود همخطی قوی‌تر خواهد بود.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2022). Hierarchical Multiple Linear Regression using SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/hierarchical-multiple-linear-regression-spss/.php

For example, if you viewed this guide on 12^th January 2022, you would use the following reference

GraphPad Statistics (2022). Hierarchical Multiple Linear Regression using SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/hierarchical-multiple-linear-regression-spss/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.