براورد منحنی Curve Estimation رگرسیونی در نرم افزار SPSS

*** توضیحات برگرفته شده از کتاب روش های پیشرفته آماری و کاربردهای آن***

 

مثلا برای مدل رگرسیون با یک کمیت مستقل، به جای تعریف مدل به صورت Y =  β₀ + β₁X₁+ ε که یک رابطه رگرسیونی خطی ساده است، مدلی به صورت زیر تعریف می‌کنیم.

Y =  β₀ + β₁ g(X)+ ε

به عنوان مثال می‌توانیم g(X) را به هر یک از صورت‌های زیر تعریف کنیم و مدل رگرسیون مربوطه را به دست آوریم.

g(X) = ln|X|  →  Y =  β₀ + β₁ ln |X|+ ε     (Logarithmic)           

g(X) =1⁄X →  Y =  β₀ + β₁ 1⁄X+ ε     (Inverse)           

g(X) =(X, X²) →  Y =  β₀ + β₁ X + β₂X²  + ε     (Quadratic)           

g(X) =(X, X², X³) →  Y =  β₀ + β₁ X + β₂X² + β₃X³  + ε     (Cubic)           

 

برایتان جالب خواهد بود که بگوییم ما تمام این مدل‌ها را مدل‌های رگرسیون خطی می‌نامیم. در واقع هر نوع تبدیلی که بر روی کمیت‌های مستقل انجام شود، یعنی تبدیل X به g(X) همچنان مدل را خطی نگه می‌دارد.

در حقیقت ما مدل‌هایی را غیرخطی می‌نامیم که پارامترها (و نه کمیت‌ها) به صورت غیرخطی در مدل رگرسیون حضور داشته باشند. برخی از مدل‌های رگرسیون غیرخطی در ادامه آمده است.

Y =  β₀ e^β1 X  + ε                    

Y =  β₀ X^β1  + ε                    

Y =  β₀ +  β₁^X  + ε                    

Y = (e^{β0 +  β1X} ⁄1+e^{β0 +  β1X})+ ε                    

در  این متن آموزشی ما به دنبال بین تبدیل X به g(X) هستیم. در واقع موضوع ما مدل‌های رگرسیون غیرخطی نیست، بلکه همان رگرسیون خطی است. با این حال ما می‌خواهیم X را به تابعی مانند g(X) تبدیل کنیم و سپس بین Y و g(X) مدل رگرسیون خطی به دست بیاوریم.

این کار را با استفاده از نرم‌افزار SPSS و بخش با نام Curve Estimation یا همان براورد منحنی، انجام خواهیم داد.

مسیر انجام این نوع تحلیل در نرم‌افزار SPSS به صورت زیر است.

 Analyze → Regression→ Curve Estimation

 

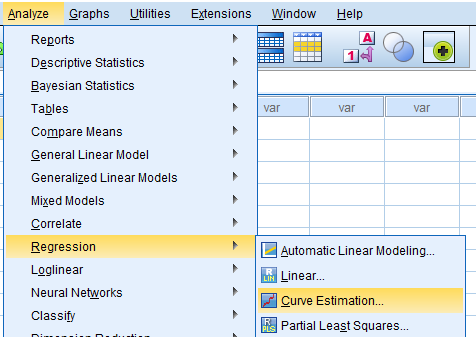
مثال براورد منحنی

 فایل مثال  از اینجا می‌توانید فایل Curve Estimation را دریافت و دانلود کنید.

در داده‌های فایل ISI & Research GDP، که به منظور تحلیل براورد منحنی در این مثال از آن استفاده می‌کنیم، سهم پژوهش از تولید ناخالص داخلی 19 کشور در برابر تعداد مقالات ISI این کشورها برحسب واحد هزار مقاله علمی، مورد بررسی قرار گرفته است. در پی آن هستیم که با توجه به سهم پژوهش در تولید ناخالص داخلی آن‌ها، ارتباطی میان این کمیت و تعداد مقالات نمایه شده‌ برقرار کنیم.

در تصویر زیر می‌توانید، فایل دیتا را مشاهده کنید.

 

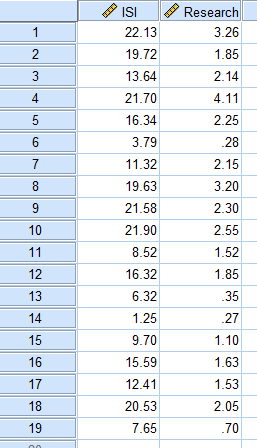
حال بیایید با استفاده از مسیر بالا، وارد پنجره Curve Estimation شویم. در تصویر زیر می‌توانید این پنجره را ببینید.

 

 

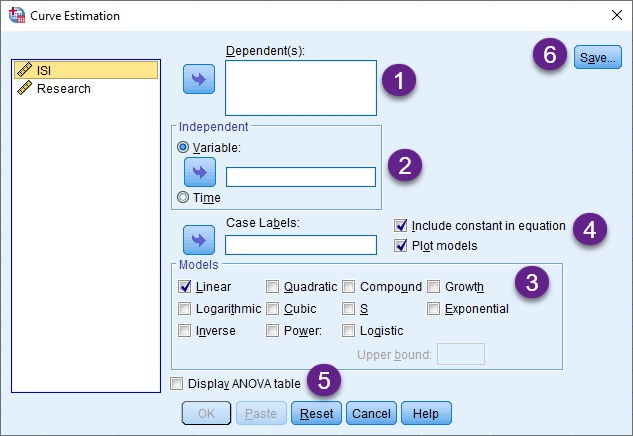
 1- Dependent(s) 

در این کادر، کمیت وابسته مدل رگرسیونی یا همان Y را قرار می‌دهیم. در این مثال ISI کمیت وابسته ما خواهد بود. نکته جالب توجه این است که می‌توان به تعداد بیشتر از یک Dependent Variable در این کادر قرار داد. البته نرم‌افزار به ازای هر کدام از آن‌ها برای ما یک مدل رگرسیونی جداگانه براورد می‌کند.

 Independent -2 

خیلی ساده در این کادر، Independent Variable یا همان X قرار می‌گیرد. نکته این است که در مسیر Curve Estimation فقط می‌توانیم به تعداد یک X قرار دهیم.

اگر مطالعه ما بررسی Dependent در طول زمان بود، گزینه Time را انتخاب می‌کنیم. با این کار ما دیگر کمیتی با نام X نخواهیم داشت و تایم یا T همان نقش X را در مدل رگرسیونی ما خواهد داشت. جالب توجه است، آیا این کار شما را به یاد سری‌های زمانی Time Series نمی‌اندازد؟ پاسخ مثبت است. سری زمانی نیز همین‌گونه است، بررسی یک Variable در طول زمان. پس خیلی ساده با همین گزینه Curve Estimation در نرم‌افزار SPSS می‌توانید یک مدل سری زمانی به دست بیاورید.

 3- Models 

در این کادر انواع تبدیل‌های g(X) که از آن نام بردیم، وجود دارد. با انتخاب هر کدام از آن‌ها (محدودیتی در تعداد انتخاب وجود ندارد.) مدل رگرسیون خطی بین Y و g(X) انتخاب شده، ایجاد می‌شود. مثلا اگر گزینه Inverse را انتخاب کنیم، X به وارون خود تبدیل می‌شود و مدل رگرسیونی ما به صورت زیر خواهد بود.

g(X) =1⁄X →  Y =  β₀ + β₁ 1⁄X+ ε          

 

 در ادامه فرمول و مدل رگرسیونی هر کدام از توابع موجود در این بخش آمده است. علامت * به معنای ضرب و ** به معنای توان است.

 Linear.  Y = b0 + (b1 * X)           

Logarithmic.  Y = b0 + (b1 * ln(X))          

 Inverse.  Y = b0 + (b1 / X)         

Quadratic.  Y = b0 + (b1 * X) + (b2 * X**2)        

Cubic.  Y = b0 + (b1 * X) + (b2 * X**2) + (b3 * X**3)        

 Power.  Y = b0 * (X**b1) or ln(Y) = ln(b0) + (b1 * ln(X))        

Compound.  Y = b0 * (b1**X) or ln(Y) = ln(b0) + (ln(b1) * X)       

 S-curve.  Y = e**(b0 + (b1/X)) or ln(Y) = b0 + (b1/X)       

 Logistic.  Y = 1 / (1/u + (b0 * (b1**X))) or ln(1/y-1/u) = ln (b0) + (ln(b1) * X) where u is the upper boundary value       

 Growth.  Y = e**(b0 + (b1 * X)) or ln(Y) = b0 + (b1 * X)      

 Exponential.  Y = b0 * (e**(b1 * X)) or ln(Y) = ln(b0) + (b1 * X)      

 

به این ترتیب ما می‌توانیم انواع تبدیل‌های X به تابعی از X را مشاهده کنیم. مدل رگرسیونی را برازش دهیم و سپس با مشاهده نتایج به دست آمده که در ادامه به آن می‌پردازیم، بهترین مدل رگرسیونی مبتنی بر g(X) را انتخاب کنیم.

 4- Constant & Plot 

با انتخاب گزینه‌های این بخش که البته به صورت پیش‌فرض در نرم‌افزار انتخاب شده‌اند، می‌توانیم ضرایب ثابت یا همان  β₀  را در مدل رگرسیونی خود داشته باشیم. همچنین می‌توانیم گراف و نمودار مدل رگرسیونی را مشاهده کنیم.

 5- ANOVA 

جنانجه علاقمند باشیم، جدول آنالیز واریانس مدل رگرسیونی خود را نیز مشاهده کنیم، این گزینه را انتخاب می‌کنیم.

 6- Save 

جنانجه تب save را بزنیم، وارد پنجره زیر می‌شویم

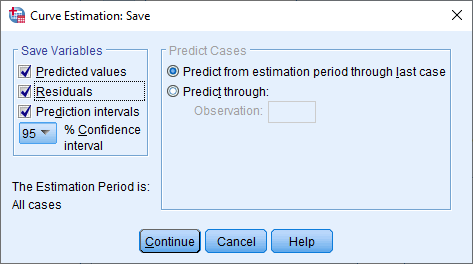
در این پنجره می‌توانیم گزینه‌های نمایش و به دست آوردن مقادیر پیش‌بینی شده، باقیمانده‌های مدل رگرسیونی انتخاب شده و فواصل اطمینان برای مقادیر پیش‌بینی شده را مشاهده کنیم. نتایج این بخش به عنوان ستون‌هایی جدید به فایل دیتا اضافه خواهد شد.

خب، حال بیایید بر روی داده‌های این مثال، چند تابع g(X) به صورت تصویر زیر انتخاب کنیم. ما ISI را در کادر Dependent(s) و Research را در کادر Independent قرار داده‌ایم.

 

 

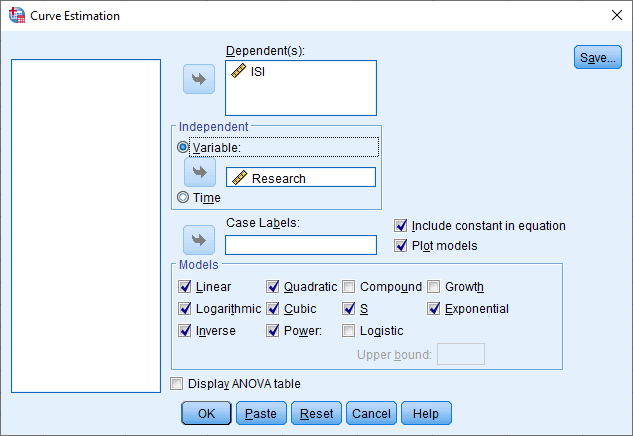
حال بیایید در ادامه نتایج به دست آمده را بررسی کنیم.

 

تحلیل نتایج

 Curve Estimation 

 

در ابتدا و در جدول زیر با نام Model Description اسامی کمیت‌های وابسته و مستقل و معادلات رگرسیونی مورد استفاده بیان شده است.

 

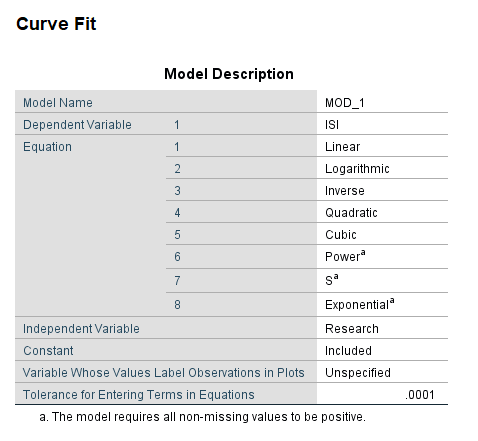
همان‌گونه که مشاهده می کنید، هشت مدل رگرسیونی برای این داده‌ها، به دست آورده‌ایم.

در جدول دیگر با نام Variable Processing Summary تعداد داده‌های مثبت، صفر و منفی و همچنین داده‌های گمشده به ازای هر کدام از کمیت‌های وابسته یا مستقل، مشخص شده است.

 

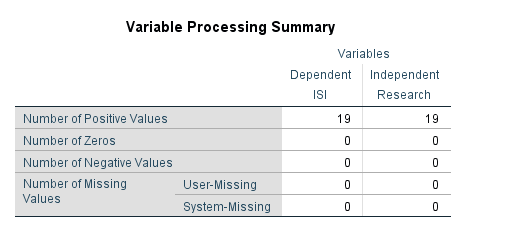
همان‌گونه که در جدول Variable Processing Summary می‌بینید، تعداد 19 داده مثبت هم در ISI و هم در Research وجود دارد.

جدول زیر با نام Model Summary and Parameter Estimates مهمترین بخش تحلیل براورد منحنی‌ها به حساب می‌آید.

 

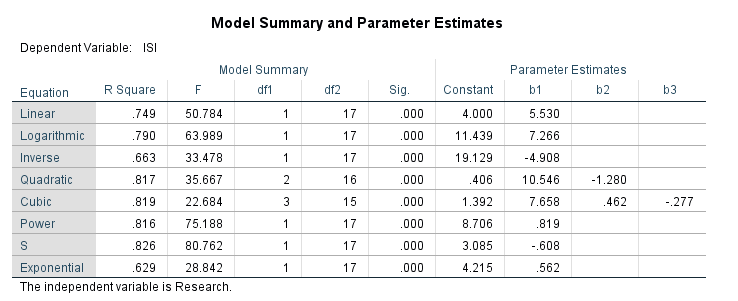
در این جدول ضریب تعیین R Square، مقدار احتمال معناداری مدل رگرسیونی Sig و ضرایب رگرسیونی براورد شده به ازای هر کدام از معادله‌های 8گانه انتخاب شده، به دست آمده است.

به عنوان مثال به دست می‌آید که معادله رگرسیون خطی ساده بین ISI و Research به صورت زیر است.

 Linear.  ISI = 4.0 + (5.53 * Research)           

اندازه R Square این مدل رگرسیونی نیز برابر با 0.749 به دست آمده است.

سوال

یک سوال مهم این است که خب، کدام یک از این مدل‌های رگرسیونی بهتر است؟

به منظور پاسخ به این سوال لازم است ابتدا ستون Sig را نگاه کنیم. هر کدام که معنادار بود مدل بهتری است. منظور از معناداری نیز این است که عدد ستون Sig از سطح معنی‌دااری که قبلاً در نظر گرفتیم و معمولاً برابر با 0.05 است، کمتر باشد.

در مرحله بعد و در بین مدل‌هایی که معنادار شده است، نگاه می‌کنیم که کدامیک ضریب تعیین یا همان R Square بالاتری دارد. هر کدام که بالاتر بود، آن معادله بهتر است.

خب، همان گونه که در جدول Model Summary and Parameter Estimates دیده می شود، برای تمام مدل‌ها اندازه عددی Sig < 0.001 شده است. پس همه معادله‌های رگرسیونی بین ISI و Research معنادار شده است. بنابراین دقت می‌کنیم که کدامیک از R Square ها از بقیه بزرگتر است.

مشاهده می‌شود که ضریب تعیین برای معادله با نام S از بقیه بزرگتر و برابر با 0.826 شده است. بنابراین می‌توانیم بگوییم این معادله از بقیه بهتر است.

رابطه آماری معادله S به صورت زیر است.

 S-curve.  Y = e**(b0 + (b1/X)) or ln(Y) = b0 + (b1/X)       

بنابراین رابطه رگرسیونی بین بین ISI و Research به صورت زیر در بهترین حالت خواهد بود.

 S-curve.  ln(ISI) = 3.085 – (0.608/Research)       

این رابطه بیان می‌کند که برای رسیدن به بهترین معادله بین ISI و Research، ابتدا از ISI، لگاریتم (Ln) بگیر و سپس Research را وارون کن. در پایان نیز بین Ln(ISI) و وارون Research رابطه رگرسیون خطی به دست بیاور.

در گراف زیر همه 8 مدل رگرسیونی به دست آمده بین ISI و Research رسم شده است. مدل S را نیز می‌توانید ببینید.

 

 

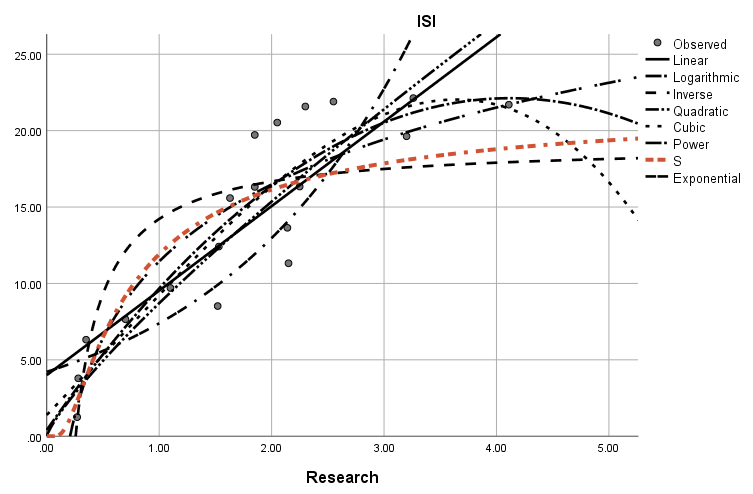
همچنین به صورت جداگانه در گراف زیر مدل S بیان شده است.

 

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2021). Curve Estimation Regression in SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/curve-estimation-spss/.php

For example, if you viewed this guide on 12^th January 2022, you would use the following reference

GraphPad Statistics (2021). Curve Estimation Regression in SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/curve-estimation-spss/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.