Binary Probit در مسیر Generalized Linear Models نرم‌افزار SPSS

 Probit Regression 

دریافت آموزش تحلیل‌های رگرسیون پروبیت با SPSS

شامل 65 دقیقه ویدئو، فایل‌های مثال، دیتا و نتایج نرم‌افزار SPSS

 

قبلاً و در لینک (رگرسیون لجستیک باینری Binary Logistic Regression در نرم‌افزار SPSS) به بیان مدل لجیت Logit در طراحی مدل رگرسیونی اشاره کردیم. در آن‌جا گفتیم که اگر کمیت وابسته ما یعنی Y دارای توزیع باینری باشد، یعنی صرفاً دو حالت بپذیرد، از مدل رگرسیون لجستیک استفاده می‌کنیم.

رگرسیون پروبیت که مدل پروبیت نیز نامیده می‌شود، همانند مدل لجیت، برای مدل‌سازی کمیت‌های وابسته Dependent Variable دوگانه یا باینری استفاده می‌شود. با این تفاوت که در در رگرسیون پروبیت، تابع توزیع نرمال استاندارد تجمعی برای مدل‌سازی استفاده می‌شود، یعنی فرض می‌کنیم

$ \displaystyle P\left( {Y=1|X} \right)=P\left( {Y=1|{{\beta }_{0}}+\beta X} \right)=\Phi \left( {{{\beta }_{0}}+\beta X} \right)$

به معنای اینکه برای به دست آوردن احتمال رخداد پیشامد مورد نظر (Y=1) از یک احتمال شرطی بر روی X ها استفاده می‌کنیم. این احتمال شرطی نیز به صورت یک مدل رگرسیونی با استفاده از توزیع نرمال تجمعی تعریف می‌شود.

نکته‌ای که در اینجا وجود دارد و بر مبنای آن می‌توانیم رابطه‌ای بین رگرسیون پروبیت و محاسبه چندک‌ها به دست بیاوریم این است که $ \displaystyle {{{\beta }_{0}}+\beta X}$ در واقع نقش همان چندک z را در تابع توزیع نرمال تجمعی، بازی می‌کنند. یعنی اگر رابطه زیر را داشته باشیم

$ \displaystyle \Phi \left( z \right)=P\left( {Z\le z} \right)\begin{array}{*{20}{c}} , & {Z\sim N\left( {0,1} \right)} \end{array}$

بنابراین می‌توانیم به سادگی رابطه زیر را بنویسیم.

$ \displaystyle \Phi \left( {{{\beta }_{0}}+\beta X} \right)=P\left( {Z\le {{\beta }_{0}}+\beta X} \right)\begin{array}{*{20}{c}} , & {Z\sim N\left( {0,1} \right)} \end{array}$

حال اگر ما بتوانیم X ای را بیابیم که احتمال بالا را برابر با یک عدد خاص مثلاً p به دست بیاورد، آن X همان چندک p خواهد بود. یعنی رابطه زیر برقرار است

$ \displaystyle \Phi \left( {{{\beta }_{0}}+\beta {{X}_{{p}}}} \right)=P\left( {Z\le {{\beta }_{0}}+\beta {{X}_{{p}}}} \right)=p$

ما از این روش جهت محاسبه LD50 یعنی میانه دوز کشنده در لینک (محاسبه LD50 با استفاده از رگرسیون پروبیت Probit Regression) استفاده کردیم.

همچنین در لینک (مدل رگرسیون پروبیت Probit Regression در نرم افزار SPSS) به آموزش رگرسیون پروبیت با استفاده از مسیر Regression → Probit پرداختیم.

در این مقاله قصد داریم با استفاده از ماژول Generalized Linear Models به بیان مثال و تحلیل با استفاده از مدل رگرسیون پروبیت، بپپردازیم. این مسیر به ما قابلیت‌های بیشتری جهت انجام تحلیل پروبیت ارایه می‌دهد، ضمن اینکه نحوه ورود داده‌ها و اطلاعات به نرم‌‌افزار نیز در آن ساده‌تر است.

مثال رگرسیون پروبیت باینری

 Example 

در یک مطالعه که بر روی 400 نفر انجام شده، نتایجی مانند قبولی در آزمون کارشناسی ارشد، معدل و نمره زبان و همچنین نوع دانشگاه آن‌ها (دولتی یا غیر دولتی) به دست آمده است.

هدف ما در این مطالعه این است که زابطه‌ای بین قبولی در آزمون ارشد با معدل، نمره زبان و نوع دانشگاه به دست بیاوریم. از آن‌جا که قبولی در آزمون، یک فرایند باینری (قبول یا رد) است، بنابراین از مدل رگرسیون پروبیت باینری استفاده می‌کنیم.

در تصویر زیر می‌توانید داده‌های این مثال را مشاهده کنید. علاقمند بودید فایل دیتا این مقاله را می‌توانید از اینجا Binary Probit دریافت کنید.

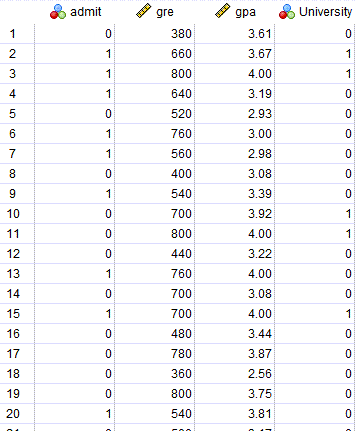
در این داده‌ها، ستون Admit=1 قبول شدن در آزمون کارشناسی ارشد را نشان می‌دهد. ستون‌های gpa و gre به ترتیب  معدل و نمره زبان دانشجویان و ستون University=1 نوع دانشگاه (دولتی) را بیان می‌کند

جهت به دست آوردن مدل رگرسیون پروبیت باینری در نرم‌افزار SPSS از مسیر زیر استفاده می‌کنیم.

Analyze → Generalized Linear Models → Generalized Linear Models 

تنظیمات نرم‌افزار در پروبیت باینری

 Setting 

هنگامی که به مسیر بالا در نرم‌افزار SPSS می‌رویم، پنجره زیر با نام Generalized Linear Models برای ما باز می‌شود.

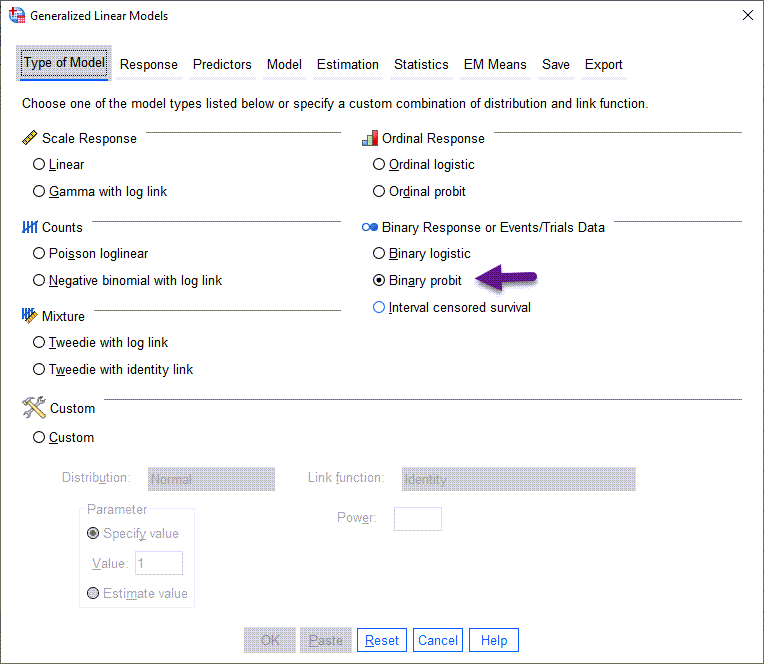
در این پنجره و از بخش Binary Response or Events/Trials Data گزینه Binary Probit را انتخاب می‌کنیم. در ادامه من درباره‌ی سایر تب‌های مورد نیاز در این پنجره صحبت می‌کنم.

بر روی تب  بزنید. وارد پنجره زیر می‌شوید.

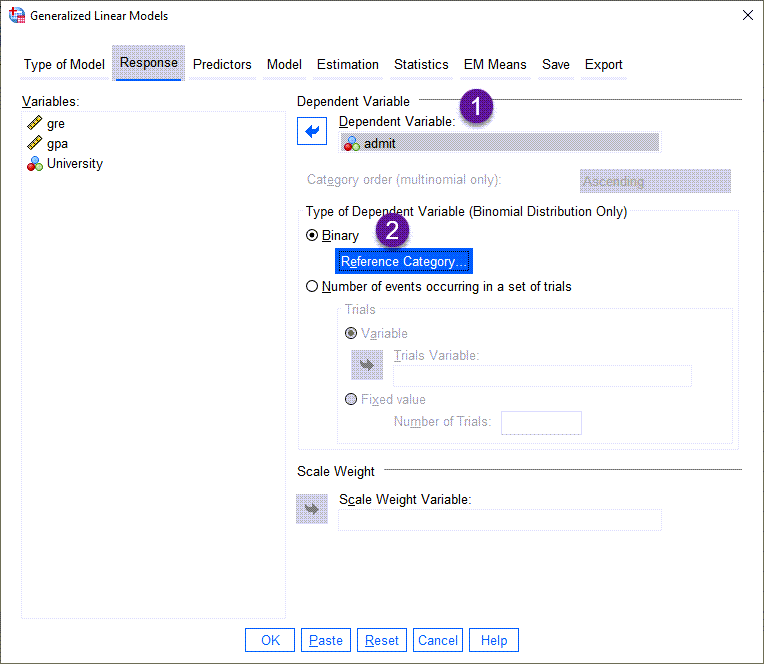
1. در این تب لازم است، کمیت پاسخ Response مدل رگرسیون باینری پروبیت، تعیین شود. از آن‌جا که ما می‌خواهیم زابطه بین قبولی در آزمون ارشد و سایر Xها را به دست بیاوریم، بنابراین Admit را در کادر Dependent Variable قرار می‌دهیم.
2. در بخش Type of Dependent Variable (Binomial Distribution Only) لازم است گروه رفرنس (یکی از کدهای صفر یعنی قبول نشدن در آزمون و یا کد یک به معنای قبول شدن در آزمون) را تعریف کنیم.

بر روی تب  می‌زنیم تا وارد پنجره زیر شویم.

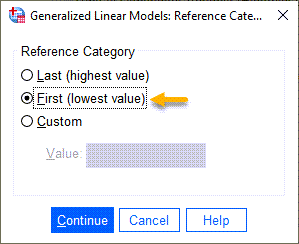
من در این مثال قصد دارم پیشامد مورد نظر خود را قبول شدن در آزمون قرار دهم. بنابراین رفرنس را کد صفر یعنی قبول نشدن قرار می‌دهم. برای انجام این کار گزینه First (lowest value) انتخاب می‌شود.

بر روی تب  بزنید. وارد پنجره زیر می‌شوید.

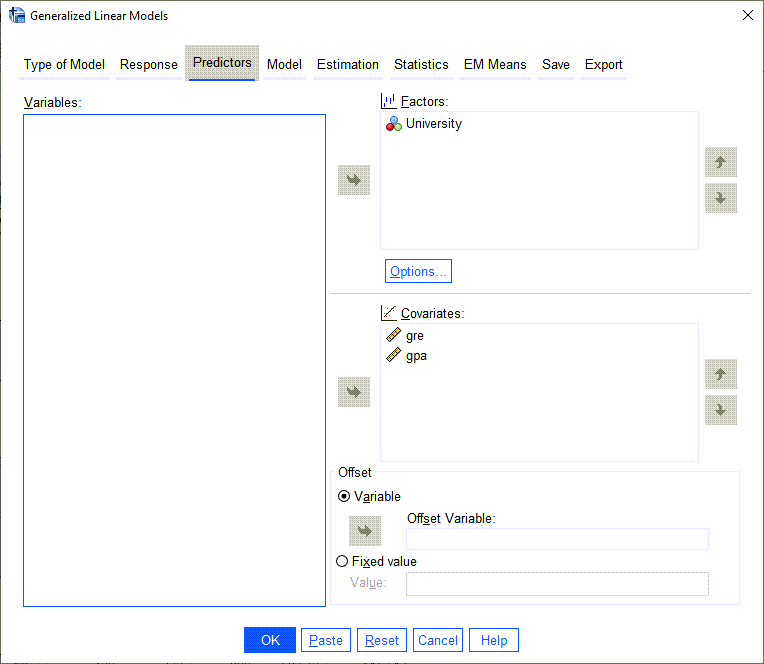
در تب Predictors لازم است X های مدل باینری پروبیت را به نرم‌افزار معرفی کنیم. معمولاً کمیت‌های اسمی و رتبه‌ای به عنوان Factor و کمیت‌های عددی Scale به عنوان Covariate در این مدل قرار می‌گیرند. ما هم در پنجره بالا همین کار را انجام دادیم. یعنی University که نشان‌دهنده نوع دانشگاه (دولتی یا غیردولتی) است در بخش Factors و gre و gpa در بخش Covariates قرار می‌گیرند.

در مرحله‌ی بعد بر روی تب  بزنید تا وارد پنجره زیر شوید.

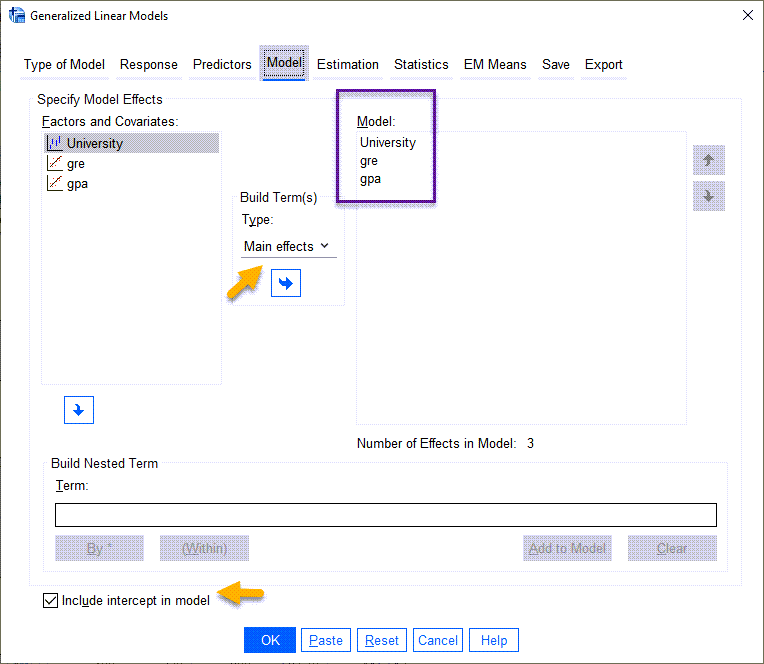
در این پنجره هر سه X مدل رگرسیون پروبیت باینری یعنی University، gpa و gre را در کادر Model قرار می‌دهیم.

همچنین صرفاً می‌خواهیم اثرات اصلی Main effects آن‌ها را به دست بیاوریم و با Interactionها مثلا اثر متقابل gpa*gre کاری نداریم. به همین دلیل در بخش Type گزینه Main effects را انتخاب می‌کنیم. تیک گزینه Include intercept in model را هم که به صورت پیش فرض نرم‌افزار SPSS قرار دارد، انتخاب می‌کنیم.

با سایر گزینه‌ها و تب‌های نرم‌افزار نیز کاری نداریم و OK می‌کنیم.

نتایج تحلیل پروبیت باینری

 Binary Probit Results 

در ابتدای نتایج و خروجی‌های نرم‌افزار SPSS جدول Model Information قرار دارد.

در این جدول بیان می‌شود که Dependent Variable مطالعه admit است. توزیع احتمال نیز به دلیل اینکه admit به صورت باینری (قبولی یا رد در آزمون) است، دوجمله‌ای Binomial تعریف می‌شود. همچنین از تابع رگرسیونی Probit استفاده کرده‌ایم.

در جدول Categorical Variable Information اطلاعات توصیفی شامل تعداد و درصد به ازای هر کدام از گزوه‌های کمیت‌های اسمی یعنی admit (که نقش Dependent Variable را دارد) و University (که نقش Factor را دارد) به دست آمده است.

به عنوان مثال نتایج جدول بالا نشان می‌دهد 127 نفر (31.8%) در آزمون قبول شده‌اند. 65 نفر (16.3%) نیز در دانشگاه دولتی تحصیل می‌کرده‌اند.

در جدول Continuous Variable Information آماره‌های توصیفی برای کمیت‌های پیوسته مطالعه یعنی gre و gpa به دست آمده است.

در جدول Goodness of Fit نتایجی مبنی بر نیکویی برازش به دست آمده است.

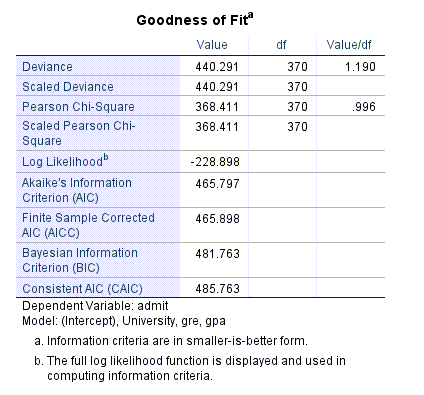
با نتایج جدول بالا چندان کاری نداریم. دلیل اصلی این مطلب این است که جدول بالا فاقد آزمون آماری و در نتیجه مقدار احتمال است که نرم‌افزار SPSS در ستونی با نام Sig نشان می‌دهد. در عوض جدول بعدی نتایج با نام Omnibus Test دارای آزمون آماری است. آن را ببینید.

در این جدول مدل برازش شده (در اینجا رگرسیون پروبیت باینری) با مدل فقط شامل ضریب ثابت (یعنی بدون هیچ‌کدام از Xها) مقایسه و آزمون شده است. نتیجه Omnibus Test نشان می‌دهد، مدل رگرسیونی برازش شده معنادار است. مفهوم این جمله این است که حداقل یکی از Xها دارای تاثیر معنادار بر قبولی در آزمون ارشد هستند.

در جدول بعدی با نام Tests of Model Effects تاثیر هر کدام از X ها به صورت جداگانه بر روی Y (قبولی در امتحان ارشد) آزمون شده‌اند. آن را ببینید.

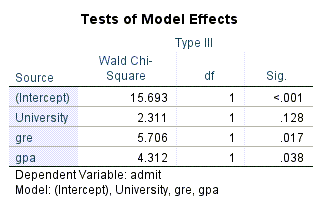
نتایج جدول بالا نشان می‌دهد نوع دانشگاه (دولتی یا غیردولتی) تاثیر معنادار بر Y ندارد (P-value=0.128). با این حال نمره زبان (P-value=0.017) و معدل دانشجو در مقطع لیسانس (P-value=0.038) دارای تاثیر معنادار بر قبولی در آزمون ارشد است.

جدول بعدی با نام Parameter Estimates در ادامه آمده است. تصویر آن را بینید.

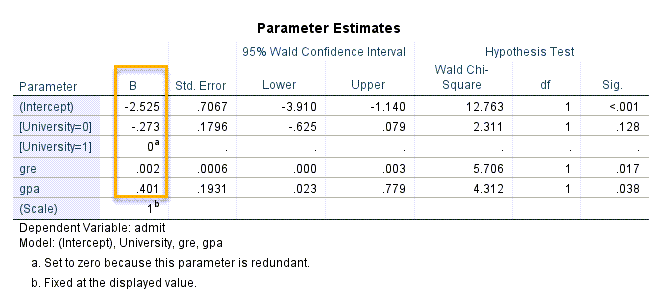
بر مبنای نتایج جدول بالا، مدل رگرسیون پروبیت، به صورت زیر خواهد بود.

$ \displaystyle P\left( {Y=1|X} \right)=\Phi \left( {{{\beta }_{0}}+{{\beta }_{1}}{{X}_{1}}+{{\beta }_{2}}{{X}_{2}}+{{\beta }_{3}}{{X}_{3}}} \right)=\Phi \left( {-2.525-0.273University+0.002gre+0.401gpa} \right)$

خوب است بدانیم که در این مدل منظور از P(Y=1) همان احتمال پیشامد (در این مثال قبولی در آزمون ارشد) مورد بررسی است که ما آن را به صورت یک مدل رگرسیون پروبیت، طراحی کردیم.

مثبت بودن ضریب رگرسیونی gpa (b=0.401)، بیانگر آن است که افزایش معدل دانشجویان، به افزایش احتمال پیشامد (قبولی در آزمون) منجر می‌شود. این نتیجه معنادار به دست می‌آید (P-value = 0.038).

یافته دیگر این است که gre نیز تاثیر معنادار و قوی بر قبولی در آزمون کارشناسی ارشد، در بین دانشجویان مورد بررسی دارد (b=0.002, P-value =0.017).

با این حال و همان‌گونه که قبلاً نیز گفتیم، نوع دانشگاه فاقد تاثیر معنادار بر قبولی در آزمون است. هر چند ضریب رگرسیونی آن منفی به دست آمده است (b=-0.273) و نشان می‌دهد دانشگاه غیر دولتی شانس قبولی کمتری نسبت به دانشگاه دولتی دارد.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2022). Binary Probit in the path of Generalized Linear Models of SPSS software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/binary-probit-generalized-linear-models-spss/.php

For example, if you viewed this guide on 12^th January 2022, you would use the following reference

GraphPad Statistics (2022). Binary Probit in the path of Generalized Linear Models of SPSS software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/binary-probit-generalized-linear-models-spss/.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.