مدل رگرسیون پروبیت Probit Regression در نرم افزار SPSS

 Probit Regression 

دریافت آموزش تحلیل‌های رگرسیون پروبیت با SPSS

شامل 65 دقیقه ویدئو، فایل‌های مثال، دیتا و نتایج نرم‌افزار SPSS

 

قبلاً و در لینک (رگرسیون لجستیک باینری Binary Logistic Regression در نرم‌افزار SPSS) به بیان مدل لجیت Logit در طراحی مدل رگرسیونی اشاره کردیم. در آن‌جا گفتیم که اگر کمیت وابسته ما یعنی Y دارای توزیع باینری باشد، یعنی صرفاً دو حالت بپذیرد، از مدل رگرسیون لجستیک استفاده می‌کنیم.

رگرسیون پروبیت که مدل پروبیت نیز نامیده می‌شود، همانند مدل لجیت، برای مدل‌سازی کمیت‌های وابسته Dependent Variable دوگانه یا باینری استفاده می‌شود. با این تفاوت که در در رگرسیون پروبیت، تابع توزیع نرمال استاندارد تجمعی برای مدل‌سازی استفاده می‌شود، یعنی فرض می‌کنیم

$ \displaystyle P\left( {Y=1|X} \right)=P\left( {Y=1|{{\beta }_{0}}+\beta X} \right)=\Phi \left( {{{\beta }_{0}}+\beta X} \right)$

به معنای اینکه برای به دست آوردن احتمال رخداد پیشامد مورد نظر (Y=1) از یک احتمال شرطی بر روی X ها استفاده می‌کنیم. این احتمال شرطی نیز به صورت یک مدل رگرسیونی با استفاده از توزیع نرمال تجمعی تعریف می‌شود.

نکته‌ای که در اینجا وجود دارد و بر مبنای آن می‌توانیم رابطه‌ای بین رگرسیون پروبیت و محاسبه چندک‌ها به دست بیاوریم این است که $ \displaystyle {{{\beta }_{0}}+\beta X}$ در واقع نقش همان چندک z را در تابع توزیع نرمال تجمعی، بازی می‌کنند. یعنی اگر رابطه زیر را داشته باشیم

$ \displaystyle \Phi \left( z \right)=P\left( {Z\le z} \right)\begin{array}{*{20}{c}} , & {Z\sim N\left( {0,1} \right)} \end{array}$

بنابراین می‌توانیم به سادگی رابطه زیر را بنویسیم.

$ \displaystyle \Phi \left( {{{\beta }_{0}}+\beta X} \right)=P\left( {Z\le {{\beta }_{0}}+\beta X} \right)\begin{array}{*{20}{c}} , & {Z\sim N\left( {0,1} \right)} \end{array}$

حال اگر ما بتوانیم X ای را بیابیم که احتمال بالا را برابر با یک عدد خاص مثلاً p به دست بیاورد، آن X همان چندک p خواهد بود. یعنی رابطه زیر برقرار است

$ \displaystyle \Phi \left( {{{\beta }_{0}}+\beta {{X}_{{p}}}} \right)=P\left( {Z\le {{\beta }_{0}}+\beta {{X}_{{p}}}} \right)=p$

ما از این روش جهت محاسبه LD50 یعنی میانه دوز کشنده در لینک (محاسبه LD50 با استفاده از رگرسیون پروبیت Probit Regression) استفاده کردیم.

در ادامه با استفاده از نرم‌افزار SPSS به بیان مثال و تحلیل با استفاده از مدل رگرسیون پروبیت، می‌پردازیم.

مثال رگرسیون پروبیت

 Example 

در یک مطالعه تعداد دانشجویان گروه آمار 17 دانشگاه به دست آمده است. همچنین تعداد افراد قبول شده در آزمون کارشناسی ارشد، همراه با میانگین معدل و نمره زبان دانشجویان، به ازای هر دانشگاه بیان شده است.

هدف ما در این مطالعه این است که رابطه‌ای بین قبولی در آزمون ارشد با معدل و نمره زبان به دست بیاوریم. از آن‌جا که تعداد کل دانشجویان هر گروه را در اختیار داریم و همچنین قبولی در آزمون، یک فرایند باینری (قبول یا رد) است، بنابراین از مدل رگرسیون پروبیت استفاده می‌کنیم.

همچنین محقق در این مطالعه به دنبال یافتن معدلی است که بر مبنای آن بتوان گفت، 50 درصد دانشجویان با داشتن آن معدل می‌توانند در آزمون ارشد، قبول شوند.

در تصویر زیر می‌توانید داده‌های این مثال را مشاهده کنید. فایل دیتا این مقاله را می‌توانید از اینجا Probit Regression دریافت کنید.

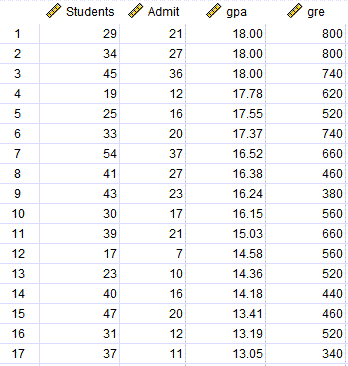
در این داده‌ها، ستون Students تعداد دانشجویان در هر دانشگاه را نشان می‌دهد. Admit تعداد دانشجویان قبول شده در آزمون کارشناسی ارشد است. همچنین ستون‌های gpa و gre به ترتیب میانگین معدل و نمره زبان دانشجویان در همان دانشگاه را نشان می‌دهد.

جهت به دست آوردن مدل رگرسیون پروبیت در نرم‌افزار SPSS از مسیر زیر استفاده می‌کنیم.

Analyze → Regression → Probit 

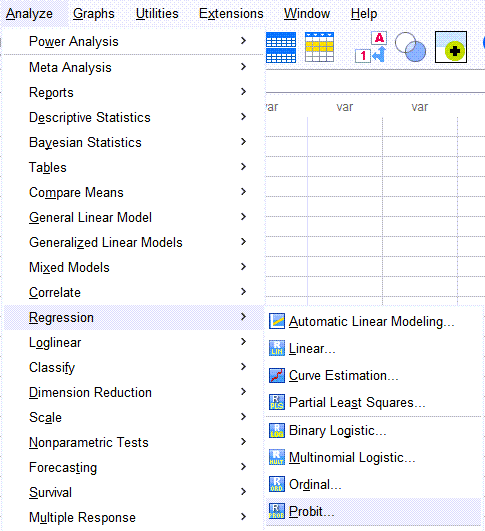
تنظیمات نرم‌افزار در مدل پروبیت

 Setting 

هنگامی که به مسیر بالا در نرم‌افزار SPSS می‌رویم، پنجره زیر با نام Probit Analysis برای ما باز می‌شود.

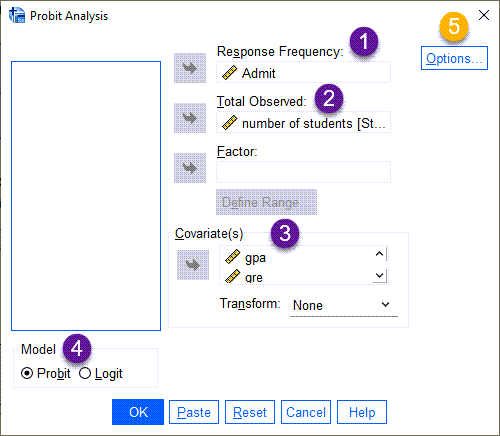
من هر کدام از بخش‌ها را با شماره قرار داده‌ام. به ترتیب هر یک را توضیح می‌دهم.

1. در بخش Response Frequency همان ستون Admit که تعداد افراد قبول شده در آزمون ارشد را نشان می‌داد، قرار می‌دهیم.
2. Total Observed تعداد آزمایش‌ها (تعداد دانشجویان) در هر دانشگاه را از ما می‌خواهد. بنابراین ستون Students را انتخاب می‌کنیم.
3. Covariate و X این مطالعه، همان نمرات gpa و gre است. بنابراین آن‌ها را در کادر Covariate قرار می‌دهیم. چنانچه علاقمند باشیم به جای کار کردن با X، با Log X کار کنیم، از کادر Transform گزینه Loge base 10 یا Natural log را انتخاب می‌کنیم. این کار اختیاری است.
4. در بخش Model، گزینه Probit را انتخاب می‌کنیم. Logit مدل دیگری است که بر مبنای تابع توزیع دوجمله‌ای Binomial کار می‌کند.
5. بر روی تب بزنید. وارد پنجره زیر می‌شوید.

در پنجره Probit Analysis Options تب‌ها و گزینه‌های مختلفی وجود دارد، بر مبنای آن‌ها خروجی و نتایج تحلیل پروبیت به دست می‌آید. به آن‌ها در این مرحله کاری نداریم و پیش‌فرض‌های نرم افزار را می‌پذیریم.

صرفاً بیان می‌کنیم که در برخی مطالعات پیشنهاد می شود عدد Significance level for use of heterogeneity factor بر روی 0.05 قرار گیرد. باید عنوان شود که این انتخاب، تاثیری بر روی نتایج و داده‌ها ندارد و فقط در خروجی‌های نتایج، عدد قرار گرفته مبنای قضاوت خواهد بود. در این زمینه به هنگام مشاهده خروجی‌ها و جداول، بیشتر صحبت خواهیم کرد. البته در این مرحله، این گزینه غیرفعال است.

نتایج تحلیل پروبیت

 Probit Results 

در ابتدای نتایج و خروجی‌های نرم‌افزار SPSS جدول Parameter Estimates آمده است. تصویر آن را در ادامه می‌بینید.

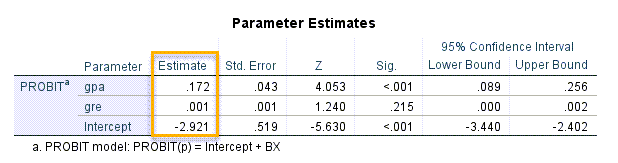
بر مبنای نتایج جدول بالا، مدل رگرسیون پروبیت، به صورت زیر خواهد بود.

$ \displaystyle P\left( {Y=1|X} \right)=\Phi \left( {{{\beta }_{0}}+{{\beta }_{1}}X} \right)=\Phi \left( {-2.921+0.172gpa+0.001gre} \right)$

خوب است بدانیم که در این مدل منظور از P(Y=1) همان احتمال پیشامد (در این مثال قبولی در آزمون ارشد) مورد بررسی است که ما آن را به صورت یک مدل رگرسیون پروبیت، طراحی کردیم.

مثبت بودن ضریب رگرسیونی gpa (b=0.172)، بیانگر آن است که افزایش معدل دانشجویان، به افزایش احتمال پیشامد (قبولی در آزمون) منجر می‌شود. این نتیجه معنادار به دست می‌آید (P-value < 0.001).

یافته دیگر این است که gre تاثیر معنادار و قوی بر قبولی در آزمون کارشناسی ارشد، در بین دانشجویان مورد بررسی ندارد (b=0.001, P-value =0.215).

جدول دیگر نتایج با نام Chi-Square Tests آمده است. آن را ببینید.

نتیجه به دست آمده نشان می‌دهد فرضیه مناسب بودن مدل رگرسیون پروبیت، تایید می‌شود (P-value=0.647).

جدول دیگر نتایج با نام Cell Counts and Residuals دیده می‌شود.

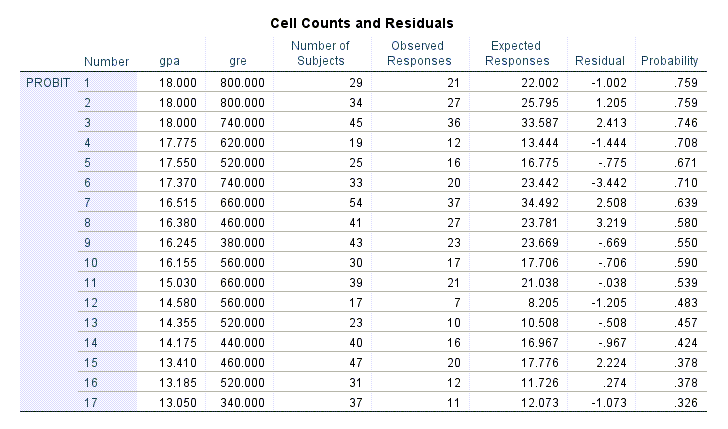
در این جدول 17 سطر (همان 17 دانشگاه مورد بررسی) آمده است. این نتایج از همان داده‌های وارد شده در نرم‌افزار به سادگی به دست می‌آیند. نتایج شامل داده‌های gpa و gre همراه با تعداد دانشجویان و تعداد قبولی‌ها به ازای هر دانشگاه می‌باشد.

ستون Expected Responses تعداد پاسخ‌ها (قبولی‌ها) بر مبنای مدل رگرسیون پروبیت را براورد کرده است. به عنوان مثال در دانشگاه هفتم که تعداد 54 دانشجو داشته و از بین آن‌ها 37 نفر قبول شده است. مدل رگرسیونی پیش بینی می‌کند تعداد قبولی‌ها 34.492 نفر است. بنابراین خطای پیش بینی که در ستون Residual آمده است برابر با 2.508 خواهد بود.

در نهایت ستون Probability وجود دارد. اعداد این ستون که بیانگر احتمال وقوع پیشامد (قبولی) در هر دانشگاه است و از تقسیم ستون Expected Responses بر تعداد دانشجویان (ستون Number of Subjects) به دست می‌آیند.

بالاتر بیان کردیم که محقق در این مطالعه به دنبال یافتن معدلی است که بر مبنای آن بتوان گفت، 50 درصد دانشجویان با داشتن آن معدل می‌توانند در آزمون ارشد، قبول شوند. در واقع ما می‌خواهیم Xای برای معدل پیدا کنیم که تابع توزیع تجمعی نرمال را برابر با 0.5 به دست بیاورد.

برای انجام این کار بار دیگر به پنجره Probit Analysis می‌رویم و تنظیمات زیر را قرار می‌دهیم.

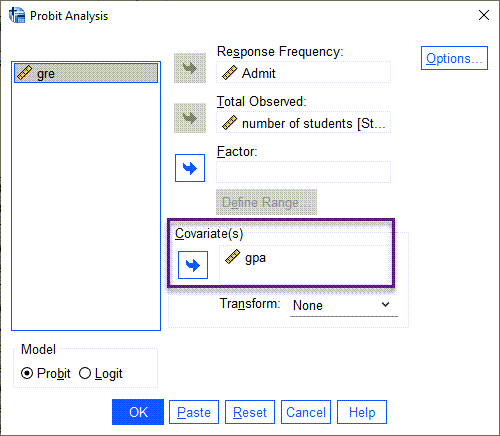
در کادر Covariate فقط gpa را قرار می‌دهیم. با انجام این کادر در تب Options گزینه Fiducial confidence intervals فعال شده است. در تصویر زیر آن را ببینید.

این گزینه به ما کمک می‌کند تا بتوانیم علاوه بر مشاهده احتمال تجمعی رخداد پیشامد به ازای هر X (معدل دانشجویان)، فواصل اطمینان X را هم ببینیم.

با Continue و سپس OK کردن، نتایج و خروجی‌های تحلیل پروبیت به دست می‌آید. برخی از نتایج مانند جداول قبلی است (البته با اعداد متفاوت). به همین دلیل درباره آن‌ها دیگر صحبت نمی‌کنیم و بر روی جدولی با نام Confidence Limits تمرکز می‌کنیم.

آنچه به دنبال آن هستیم، یعنی محاسبه X50 در نتایج این جدول آمده است. آن را ببینید.

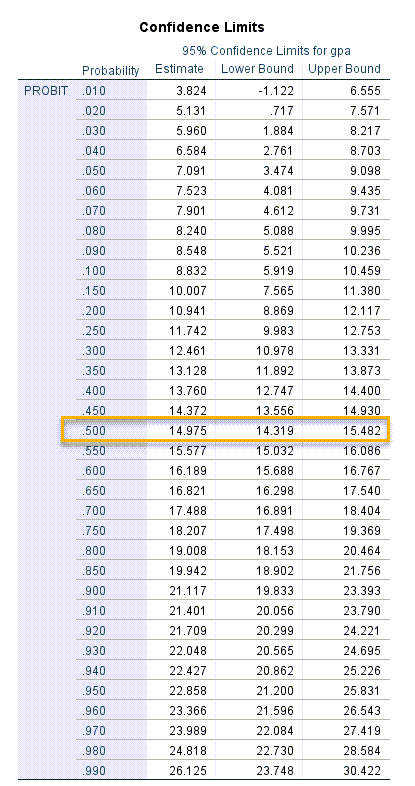
در این جدول و در ستون Probability احتمال رخداد پیشامد مورد نظر یعنی قبولی در آزمون، به ازای هر X خاص (نمره gpa) به دست آمده است. همان‌گونه که مشاهده می‌کنید عدد متناظر برای رسیدن به احتمال تجمعی 50 درصد موفقیت در آزمون، رسیدن به عدد معدل 14.975 است. فاصله اطمینان 95 درصد برای X50 نیز به صورت (15.482 ,14.319) به دست می‌آید.

خوب است این نکته را هم بدانیم که اعداد ستون Probability می‌توانند XF (F به معنای معدل صدک F) را هم برای ما براورد کنند. به عنوان مثال ما اگر بخواهیم X70 یعنی معدل مورد نیاز برای احتمال قبولی 70 درصد را به دست بیاوریم، به سادگی می‌توانیم عدد Estimate متناظر با آن را مشاهده کنیم. این عدد برابر با 17.488 خواهد بود. به این معنا که برای قبولی با احتمال 70 درصد به معدلی حود 17.49 نیاز است.

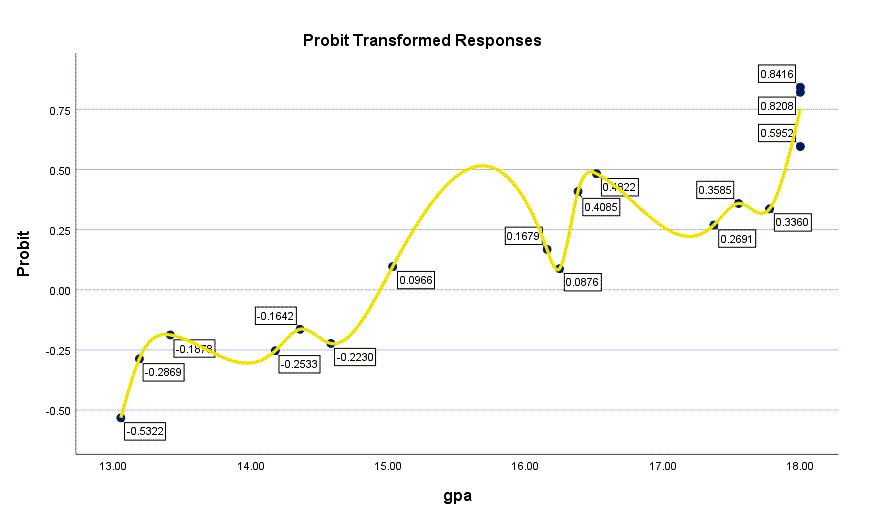
در نهایت و در انتهای نتایج نرم افزار SPSS، می‌توان گراف نمرات gpa در برابر پروبیت مدل رگرسیونی را به دست آورد.

عدد نوشته شده برای هر نمره gpa در واقع همان عدد به دست آمده از مدل رگرسیون خطی $ \displaystyle {{b}_{0}}+{{b}_{1}}{{x}_{{gpa}}}=-3.124+0.209{{x}_{{gpa}}}$ می‌باشد. از این اعداد لازم است $ Phi $ یعنی تابع توزیع تجمعی نرمال گرفته شود تا احتمال وقوع پیشامد به ازای هر دوز به دست بیاید. چنانچه به یاد داشته باشید ما این اعداد را در ستون Probability جدول Cell Counts and Residuals بیان کردیم.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2022). Probit Regression in SPSS Software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/probit-regression-spss.php

For example, if you viewed this guide on 12^th January 2022, you would use the following reference

GraphPad Statistics (2022). Probit Regression in SPSS Software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/probit-regression-spss.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.