محاسبه LD50 با استفاده از رگرسیون پروبیت Probit Regression در نرم افزار SPSS
Median Lethal Dose
LD (گاهی اوقات آن را LC نیز مینامیم) مخفف عبارت Lethal Dose ( و یا Lethal Concentration) بیانگر دوز کشنده است و به همین ترتیب LD50 مقدار دوزی است که به یکباره داده میشود و باعث مرگ 50 درصد گروهی از حیوانات آزمایش میشود. LD50 یکی از راههای اندازهگیری پتانسیل مسمومیت کوتاه مدت (سمیت حاد) یک ماده میباشد. بنابراین میتوانیم LD50 را به عنوان میانه دوز کشنده نامگزاری کنیم.
من در این مقاله به دنبال این هستم که بتوانیم با استفاده از نرمافزار SPSS و رگرسیون پروبیت Probit Regression به محاسبه LD50 بپردازم. در ابتدا توضیح کوتاهی درباره مدل رگرسیون پروبیت، ببینیم.
رگرسیون پروبیت
Probit Regression
همگی ما با یک مدل رگرسیون خطی که به صورت زیر تعریف میشود، آشنا هستیم.
$ \displaystyle y={{b}_{0}}+{{b}_{1}}{{x}_{1}}+{{b}_{2}}{{x}_{2}}+….+{{b}_{k}}{{x}_{k}}$
قبلاً و در لینک (رگرسیون لجستیک باینری Binary Logistic Regression در نرمافزار SPSS) به بیان مدل لجیت Logit در طراحی مدل رگرسیونی اشاره کردیم. در آنجا گفتیم که اگر کمیت وابسته ما یعنی Y دارای توزیع باینری باشد، یعنی صرفاً دو حالت بپذیرد، از مدل رگرسیون لجستیک استفاده میکنیم.
رگرسیون پروبیت که مدل پروبیت نیز نامیده میشود، همانند مدل لجیت، برای مدلسازی کمیتهای وابسته Dependent Variable دوگانه یا باینری استفاده میشود. با این تفاوت که در در رگرسیون پروبیت، تابع توزیع نرمال استاندارد تجمعی برای مدلسازی استفاده میشود، یعنی فرض میکنیم
$ \displaystyle P\left( {Y=1|X} \right)=P\left( {Y=1|{{\beta }_{0}}+\beta X} \right)=\Phi \left( {{{\beta }_{0}}+\beta X} \right)$
به معنای اینکه برای به دست آوردن احتمال رخداد پیشامد مورد نظر (Y=1) از یک احتمال شرطی بر روی X ها استفاده میکنیم. این احتمال شرطی نیز به صورت یک مدل رگرسیونی با استفاده از توزیع نرمال تجمعی تعریف میشود.
نکتهای که در اینجا وجود دارد و بر مبنای آن میتوانیم رابطهای بین رگرسیون پروبیت و محاسبه LD50 به دست بیاوریم این است که $ \displaystyle {{{\beta }_{0}}+\beta X}$ در واقع نقش همان چندک z را در تابع توزیع نرمال تجمعی، بازی میکنند. یعنی اگر رابطه زیر را داشته باشیم
$ \displaystyle \Phi \left( z \right)=P\left( {Z\le z} \right)\begin{array}{*{20}{c}} , & {Z\sim N\left( {0,1} \right)} \end{array}$
بنابراین میتوانیم به سادگی رابطه زیر را بنویسیم.
$ \displaystyle \Phi \left( {{{\beta }_{0}}+\beta X} \right)=P\left( {Z\le {{\beta }_{0}}+\beta X} \right)\begin{array}{*{20}{c}} , & {Z\sim N\left( {0,1} \right)} \end{array}$
حال اگر ما بتوانیم X ای را بیابیم که احتمال بالا را برابر با 0.5 و یا 50 درصد به دست بیاورد، آن X همان LD50 خواهد بود. یعنی رابطه زیر برقرار است
$ \displaystyle \Phi \left( {{{\beta }_{0}}+\beta {{X}_{{LD50}}}} \right)=P\left( {Z\le {{\beta }_{0}}+\beta {{X}_{{LD50}}}} \right)=0.5$
در ادامه با استفاده از نرمافزار SPSS به بیان مثال و نحوه به دست آوردن LD50 با استفاده از مدل رگرسیون پروبیت، میپردازیم.
مثال یافتن LD50 با رگرسیون پروبیت
Example
مطالعهای درباره اینکه یک نوع ماهی چگونه میتواند در معرض دوزهای فزاینده فلز سنگین (روی) زنده بماند، انجام شده است. مقاله منتشر شده مربوط به این مطالعه را میتوانید از اینجا (Lethal Influence of Zinc Exposure to Clarias gariepinus) دریافت کنید.
در تصویر زیر میتوانید دادههای این مثال را مشاهده کنید. این دادهها از جدول 2 مقاله بالا به دست آمده است و اثرات قرار گرفتن در معرض روی را بر روی ماهی پس از 96 ساعت نشان می دهد. فایل دیتا این مقاله را میتوانید از اینجا Probit Regression LD50 دریافت کنید.
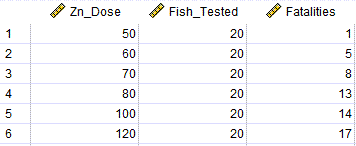
در این دادهها، ستون Zn Dose میزان دوز فلز روی را بر حسب (mg/l) نشان میدهد. Fish Tested تعداد ماهیهای مورد بررسی در هر دوز که برابر با 20 ماهی است، بیان میکند. همچنین ستون Fatalities تعداد ماهیهای از بین رفته در هر مرحله دوز را آورده است. به عنوان مثال در دوز (mg/l) 100 که تعداد 20 ماهی آزمون شده، 14 ماهی از بین رفته است.
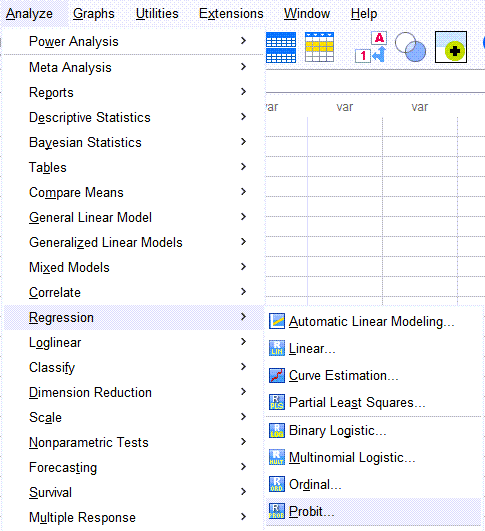
هدف من در این مثال این است که مدل رگرسیون پروبیت را بر این دادهها برازش داده و همچنین مقدار LD50 یعنی همان میانه دوز کشنده را به دست بیاوریم. برای انجام این کار در نرمافزار SPSS از مسیر زیر استفاده میکنیم.
Analyze → Regression → Probit
تنظیمات نرمافزار در مدل پروبیت
Setting
هنگامی که به مسیر بالا در نرمافزار SPSS میرویم، پنجره زیر با نام Probit Analysis برای ما باز میشود.
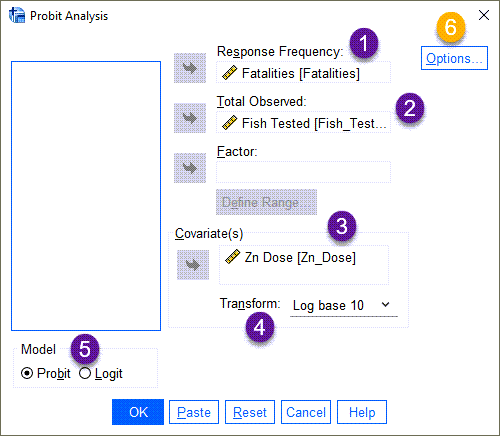
من هر کدام از بخشها را با شماره قرار دادهام. به ترتیب هر یک را توضیح میدهم.
- در بخش Response Frequency همان ستون Fatalities که تعداد ماهیهای از بین رفته در هر مرحله دوز را نشان میداد، قرار میدهیم.
- Total Observed تعداد آزمایشها (تعداد ماهیها) در هر دوز را از ما میخواهد. بنابراین ستون Fish Tested را انتخاب میکنیم.
- Covariate و X این مطالعه، همان دوزها است. بنابراین Zn Dose در کادر Covariate قرار میگیرد.
- چنانچه علاقمند باشیم به جای کار کردن با X، با Log X کار کنیم، از کادر Transform گزینه Loge base 10 را انتخاب میکنیم. این کار اختیاری است.
- در بخش Model، گزینه Probit را انتخاب میکنیم. Logit مدل دیگری است که بر مبنای تابع توزیع دوجملهای Binomial کار میکند.
- بر روی تب
 بزنید. وارد پنجره زیر میشوید.
بزنید. وارد پنجره زیر میشوید.
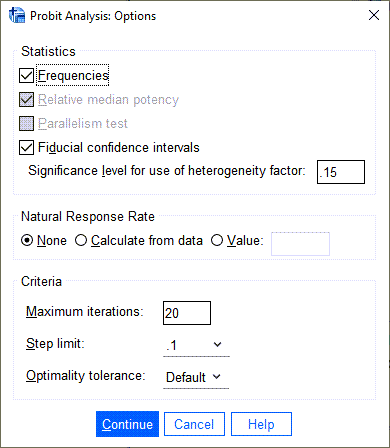
در پنجره Probit Analysis Options تبها و گزینههای مختلفی وجود دارد، بر مبنای آنها خروجی و نتایج تحلیل پروبیت به دست میآید. به آنها در این مرحله کاری نداریم و پیشفرضهای نرم افزار را میپذیریم.
صرفاً بیان میکنیم که در برخی مطالعات پیشنهاد می شود عدد Significance level for use of heterogeneity factor بر روی 0.05 قرار گیرد. باید عنوان شود که این انتخاب، تاثیری بر روی نتایج و دادهها ندارد و فقط در خروجیهای نتایج، عدد قرار گرفته مبنای قضاوت خواهد بود. در این زمینه به هنگام مشاهده خروجیها و جداول، بیشتر صحبت خواهیم کرد.
نتایج تحلیل پروبیت
Probit Results
در ابتدای نتایج و خروجیهای نرمافزار SPSS جدول Parameter Estimates آمده است. تصویر آن را در ادامه میبینید.
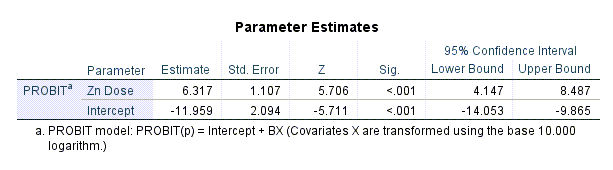
بر مبنای نتایج جدول بالا، مدل رگرسیون پروبیت، به صورت زیر خواهد بود.
$ \displaystyle P\left( {Y=1|X} \right)=\Phi \left( {{{\beta }_{0}}+{{\beta }_{1}}X} \right)=\Phi \left( {-11.96+6.32Zn\_Dose} \right)$
خوب است بدانیم که در این مدل منظور از P(Y=1) همان احتمال پیشامد (در این مثال مرگ ماهیها) مورد بررسی است که ما آن را به صورت یک مدل رگرسیون پروبیت، طراحی کردیم.
مثبت بودن ضریب رگرسیونی X یعنی همان میزان دوز فلز روی (b=6.32)، بیانگر آن است که افزایش میزان دوز، به افزایش احتمال پیشامد (مرگ ماهیها) منجر میشود. این نتیجه معنادار به دست میآید (P-value < 0.001).
جدول دیگر نتایج با نام Chi-Square Tests آمده است. آن را ببینید.

در این جدول آزمون مناسب بودن مدل رگرسیونی برازش شده، انجام شده است. در متن نوشته شده زیر جدول همان عدد 0.15 تب Options که در تنظیمات نرمافزار از ان نام بردیم، آمده است.
نتیجه به دست آمده نشان میدهد از آنجا که مقدار احتمال آزمون (P-value=0.647) بزرگتز از 0.15 است، بنابراین فرضیه مناسب بودن مدل رگرسیون پروبیت، تایید میشود و بیان میکنیم از آنجایی که سطح معنیداری بیشتر از 0.15 است، هیچ عامل ناهمگنی در محاسبه حدود اطمینان، وجود ندارد.
جدول دیگر نتایج با نام Cell Counts and Residuals دیده میشود.
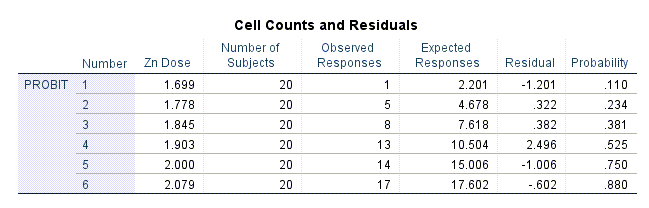
در این جدول لگاریتم دوزها به همراه تعداد آزمایشها در هر دوز و تعداد مرگهای مشاهده شده آمده است. این نتایج از همان دادههای وارد شده در نرمافزار به سادگی به دست میآیند.
ستون Expected Responses تعداد پاسخها (مرگها) بر مبنای مدل رگرسیون پروبیت را براورد کرده است. به عنوان مثال در دوز (mg/l) 80 که لگاریتم آن 1.903 شده، 13 ماهی از بین رفته است. مدل رگرسیونی پیش بینی میکند تعداد ماهیهای از بین رفته 10.504 است. بنابراین خطای پیش بینی که در ستون Residual آمده است برابر با 2.496 خواهد بود.
در نهایت ستون Probability وجود دارد. اعداد این ستون که بیانگر احتمال وقوع پیشامد (مرگ) در هر دوز است، از تقسیم ستون Expected Responses بر تعداد ماهیها (20) به دست میآیند.
- Confidence Limits
آنچه به دنبال آن هستیم، یعنی محاسبه LD50 در نتایج این جدول آمده است. آن را ببینید.
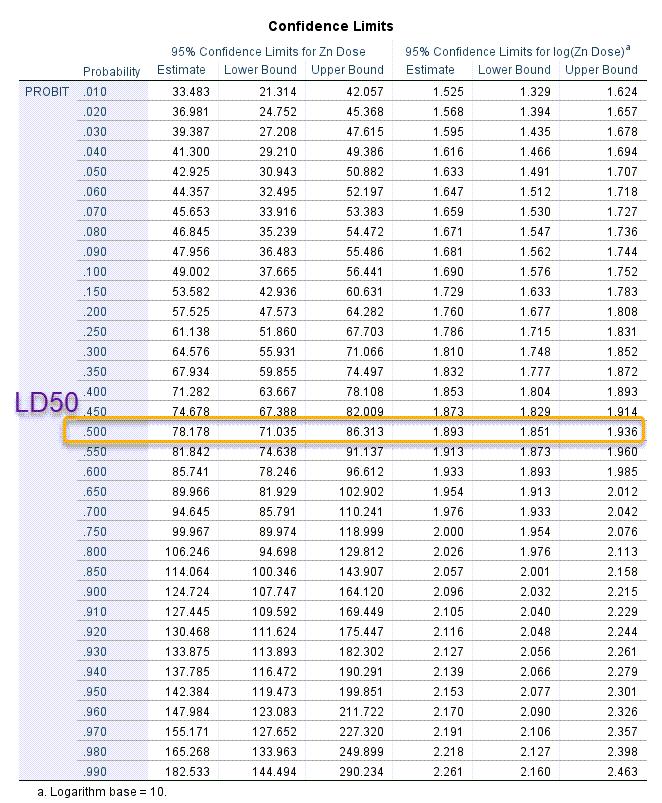
در این جدول و در ستون Probability احتمال رخداد پیشامد مورد نظر یعنی مرگر ماهیها به ازای هر X خاص (دوز فلز روی) به دست آمده است. یکبار دیگر بیایید تعریف LD50 را به یاد بیاوریم.
گفتیم که LD50 میزان دوزی است که سبب مرگ 50 درصد نمونهها میشود. بنابراین در جدول بالا کافی است احتمال 0.50 را پیدا کنیم. عدد ستون Estimate که بیانگر دوز (X) مورد نیاز برای رسیدن به احتمال متناظر با آن است، همان LD50 مورد نظر ما است. بنابراین در این مثال LD50 برابر با (mg/l) 78.178 خواهد بود. فاصله اطمینان 95 درصد برای LD50 نیز به صورت (86.313 ,71.305) به دست میآید.
علاقمند بودید، در جدول بالا میتوان نتایج برای لگاریتم دوزها و به همچنین برای Log LD50 را ببینید. اگر بخواهیم مدل پروبیت برای LD50 به دست آمده را بنویسیم، رابطه زیر را خواهیم داشت.
$ \displaystyle \Phi \left( {{{\beta }_{0}}+{{\beta }_{1}}{{X}_{{LD50}}}} \right)=\Phi \left( {-11.959+6.317{{X}_{{LD50}}}} \right)=\Phi \left( {-11.959+\left( {6.317\times 1.893} \right)} \right)=0.5$
از آنجا که مدل رگرسیونی بر مبنای لگاریتم دوزها به دست آمده است، بنابراین در رابطه بالا نیز لگاریتم LD50 آمده است.
خوب است این نکته را هم بدانیم که اعداد ستون Probability میتوانند LDF (F به معنای دوز کشنده صدک F) را هم برای ما براورد کنند. به عنوان مثال ما اگر بخواهیم LF90 یعنی دوزی که 90 درصد نمونهها را از بین میبرد، را به دست بیاوریم، به سادگی میتوانیم عدد Estimate متناظر با آن را مشاهده کنیم. این عدد برابر با (mg/l) 124.724 خواهد بود. به این معنا که استفاده از دوز حدود 125 واحد فلز روی میتواند حدود 90 درصد ماهیها را از بین ببرد.
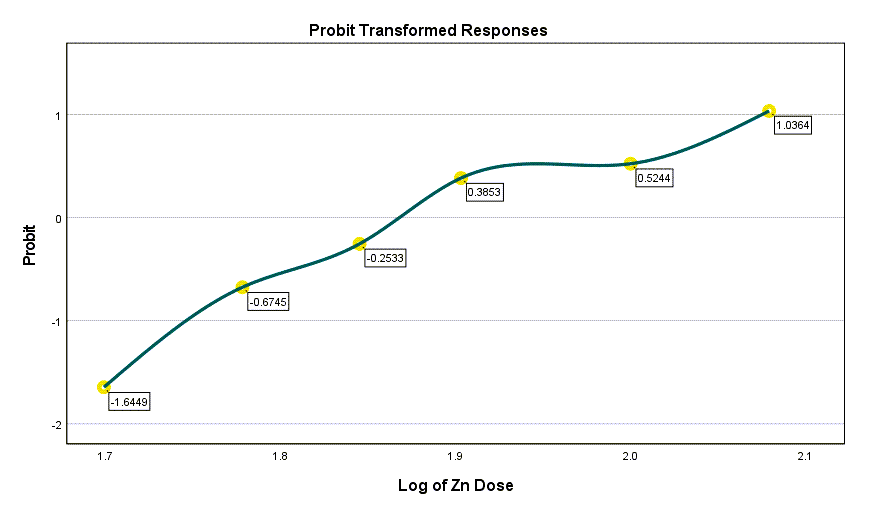
در نهایت و در انتهای نتایج نرم افزار SPSS، میتوان گراف لگاریتم دوز در برابر پروبیت مدل رگرسیونی را به دست آورد.
عدد نوشته شده برای هر دوز در واقع همان عدد به دست آمده از مدل رگرسیون خطی $ \displaystyle {{\beta }_{0}}+{{\beta }_{1}}LogX=-11.959+6.317LogX$ میباشد. از این اعداد لازم است $ \displaystyle \Phi $ یعنی تابع توزیع تجمعی نرمال گرفته شود تا احتمال وقوع پیشامد به ازای هر دوز به دست بیاید. چنانچه به یاد داشته باشید ما این اعداد را در ستون Probability جدول Cell Counts and Residuals بیان کردیم.
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2022). Calculation of LD50 using Probit Regression in SPSS Software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/ld50-probit-regression-spss.php
For example, if you viewed this guide on 12th January 2022, you would use the following reference
GraphPad Statistics (2022). Calculation of LD50 using Probit Regression in SPSS Software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/ld50-probit-regression-spss.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.


