رگرسیون چندک Quantile Regression در نرم افزار SPSS

Quantile Regression

همگی ما با یک مدل رگرسیون خطی که به صورت زیر تعریف می‌شود، آشنا هستیم.

$ \displaystyle y={{b}_{0}}+{{b}_{1}}{{x}_{1}}+{{b}_{2}}{{x}_{2}}+….+{{b}_{k}}{{x}_{k}}$

در لینک (رگرسیون خطی Linear Regression در نرم‌افزار SPSS) می‌توانید آموزش طراحی مدل رگرسیون خطی را مشاهده کنید.

آنچه در این مدل اهمیت دارد و مبنای کار ما در بیان رگرسیون چندک Quantile Regression قرار می‌گیرد این است که رابطه رگرسیونی

$ \displaystyle Y=X\beta +\varepsilon $

که در آن $ \displaystyle \beta $ ضرایب رگرسیونی و $ \displaystyle \varepsilon $ جمله خطا است، جهت براورد پارامترهای رگرسیونی، به عبارت زیر تبدیل می‌شود.

$ \displaystyle E\left( Y \right)=\hat{Y}=Xb$

نکته بسیار مهمی که در این‌جا وجود دارد این است که ما با استفاده از Xها و ضرایب رگرسیونی آن‌ها، به براورد و پیش بینی میانگین $ \displaystyle E\left( Y \right)$ کمیت پاسخ می‌پردازیم.

با این حال، در بسیاری از شرایط، ما بیشتر به میانه یا یک کمیت دلخواه از کمیت پاسخ علاقه‌مند هستیم. این مطلب اساس استفاده از رگرسیون چندک، قرار دارد. یعنی این‌که به جای براورد و پیش‌بینی میانگین کمیت پاسخ، به براورد چندک Quantile دلخواه از Y ها بپردازیم. از این رو به این مدل‌ها، رگرسیون چندک گفته می‌شود.

مدل رگرسیونی چندک به صورت زیر بیان می‌شود.

$ \displaystyle {{Q}_{q}}\left( {y|x} \right)=X{{\beta }_{q}}={{\beta }_{{0q}}}+{{\beta }_{{1q}}}{{X}_{1}}+{{\beta }_{{2q}}}{{X}_{2}}+….+{{\beta }_{{kq}}}{{X}_{k}}+\varepsilon $

ما در این مدل رگرسیونی می‌خواهیم با استفاده از X ها به براورد چندک qام، کمیت پاسخ Y بپردازیم. همان‌گونه که می‌دانیم اگر q=0.5 باشد، در این صورت مدل رگرسیونی ما به براورد میانه Y می‌پردازد.

قبل از اینکه به آموزش این نوع مدل‌ها در نرم‌افزار SPSS بپردازیم، به بیان موارد استفاده از رگرسیون چندک می‌پردازیم.

موارد استفاده از Quantile Regression

When to Use Quantile Regression?

استفاده از رگرسیون چندک در برخی موارد انجام می‌شود. در ادامه چند مورد و زمان استفاده از رگرسیون چندک، بیان شده است. آن‌ها را مرور می‌کنیم.

1. هنگامی که پیش فرض‌های رگرسیون خطی رد شود. به عنوان مثال واریانس خطاها، ثابت نباشند. در این لینک پیش‌فرض‌های تحلیل رگرسیون خطی را ببینید.

2. زمانی که در داده‌های خود یک یا چند عدد پرت Outlier Data دارید.

3. وقتی می‌خواهید به پیش‌بینی میانه یک کمیت در یک مجموعه داده بپردازید.

4. هنگامی که می‌خواهید به مقایسه چندک خاص مثلاً میانه یک کمیت وابسته، در بین چند گروه بپردازید.

4. وقتی خطاهای مدل رگرسیونی از کوچک و بزرگ شدن X و Y تاثیر می‌پذیرد. به بیان دیگر خطاها به کمیت‌های مستقل و وابسته رگرسیونی، متصل و مرتبط باشند.

5. زمانی که باقیمانده‌های مدل رگرسیون خطی، غیرنرمال باشند.

رگرسیون چندک، رابطه بین مجموعه‌ای از کمیت‌های پیش‌بینی‌کننده یا مستقل و صدک‌های خاص یا چندک‌های یک کمیت وابسته، (معمولاً میانه) را برازش می‌کند. مزیت اصلی رگرسیون چندک نسبت به رگرسیون حداقل مربعات معمولی Ordinary Least Squares Regression (OLS) به صورت زیر است.

رگرسیون چندک هیچ پیش فرضی در مورد توزیع کمیت وابسته ایجاد نمی‌کند.

رگرسیون چندک تمایل دارد در برابر تاثیر مشاهدات پرت Outlying Observations مقاومت کند.

رگرسیون چندک به طور گسترده برای تحقیقات در صنایعی مانند اکولوژی، بهداشت و درمان و اقتصاد مالی استفاده می‌شود.

به عنوان مثال، گراف زیر را ببینید. این یک گراف با داده‌های فرضی است که موارد کاربرد رگرسیون چندک را به خوبی نشان می‌دهد.

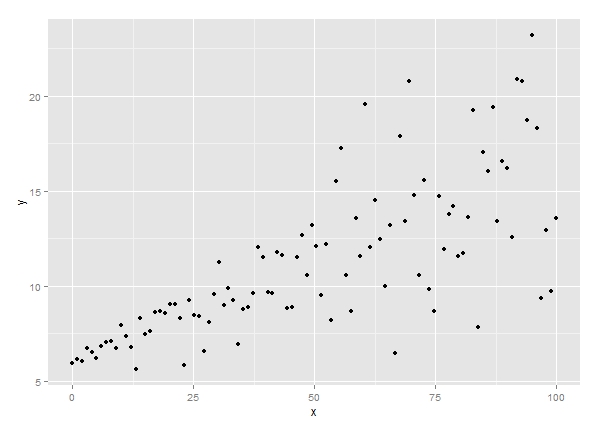
همان‌گونه که در این گراف می‌بینید با بزرگ شدن X‌ها، کمیت Y متنوع‌تر و گسترده‌تر می‌شود. این مطلب یکی از فرض‌های اصلی در انجام رگرسیون خطی یعنی باقیمانده‌های نرمال با واریانس ثابت را نقض می‌کند. در این گراف، واریانس خطاها به X بستگی دارد. در این مثال استفاده از رگرسیون خطی، اطلاع زیادی از نحوه رابطه بین X و Y در اختیار ما قرار نمی‌دهد.

در گراف زیر نتیجه رگرسیون خطی برازش شده بر این داده‌ها به همراه فواصل اطمینان خط رگرسیونی را ببینید.

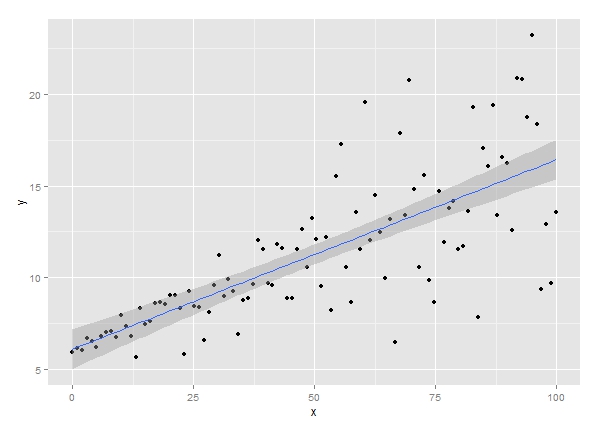
مدل رگرسیون خطی برازش شده بر داده‌های بالا، هنگامی که X کوچک است، به خوبی کار می‌کند، اما با افزایش X از میزان مناسب بودن مدل رگرسیونی کاسته می‌شود. در واقع پراکندگی داده‌ها انقدر زیاد می‌شود که مدل رگرسیون خطی پاسخگو نخواهد بود و از نقاط کمی رد می‌شود.

به عنوان مثال در همین گراف بالا اگر بخواهیم میانگین Y را هنگامی که X = 75 است براورد کنیم (یعنی کاری که در رگرسیون خطی انجام می‌دهیم، برازش میانگین Y به ازای X خاص) خط رگرسیونی و حتی فواصل اطمینان آن، با خطای زیادی همراه خواهند بود.

این مطلب که در گراف بالا نشان داده شده است، از دلایل استفاده از نوع دیگری رگرسیون را برای ما معرفی می‌کند. به معنای اینکه به جای پیش‌بینی میانگین Y، به پیش‌بینی آماره دیگری از جمله چندک‌های Y (به ویژه میانه) بپردازیم.

حال به گراف زیر نگاه کنید. در اینجا X در برابر صدک 90 کمیت Y رسم شده است.

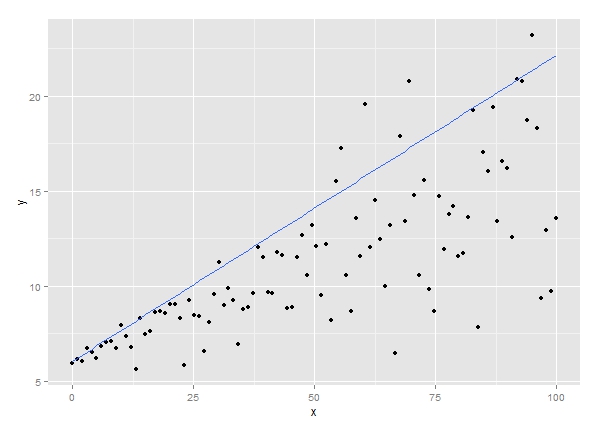
در گراف بالا یک رگرسیون چندک برای quantile = 0.90 اجرا کرده و سپس خط برازش رگرسیونی رسم شده است. می‌بینیم که پراکندگی در مورد خط رسم شده نسبتاً یکنواخت است. به نظر می‌رسد می‌توانیم براوردهای مناسبی از چندک 0.90 برای افزایش مقادیر X ارایه دهیم.

در ادامه با استفاده از نرم‌افزار SPSS به بیان مثال و تحلیل با استفاده از مدل رگرسیون چندک، می‌پردازیم.

مثال رگرسیون چندک

Example

یک محقق می‌خواهد مدل‌های رگرسیون چندک بسازد و رابطه بین چندک‌های شرطی (چارک اول q=0.25، میانه q=0.5 و چارک سوم q=0.75) هزینه‌های پزشکی به عنوان کمیت وابسته و پیش‌بینی‌کننده‌های سن، وضعیت سلامت و بیمه تکمیلی را ایجاد کند. اگر چه این موضوع ضروری نیست و به رگرسیون چندک نیز ارتباطی ندارد، با این حال هزینه‌های پزشکی به صورت لاگ تبدیل شده‌اند.

در تصویر زیر می‌توانید داده‌های این مثال را مشاهده کنید. فایل دیتا این مقاله را می‌توانید از اینجا Quantile Regression دریافت کنید.

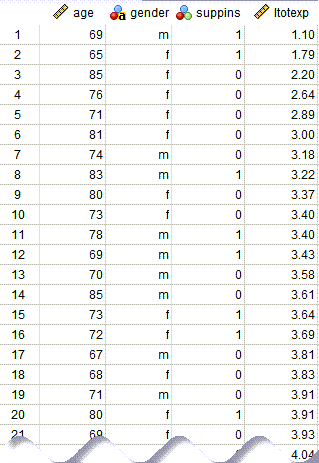
داده‌های مثال رگرسیون چندک Quantile Regression

در این داده‌ها، ستون suppins و کد 1، داشتن بیمه تکمیلی را نشان می‌دهد. ltotexp نیز همان لگاریتم هزینه‌های پزشکی است.

جهت به دست آوردن مدل رگرسیون چندک در نرم‌افزار SPSS از مسیر زیر استفاده می‌کنیم.

Analyze → Regression → Quantile

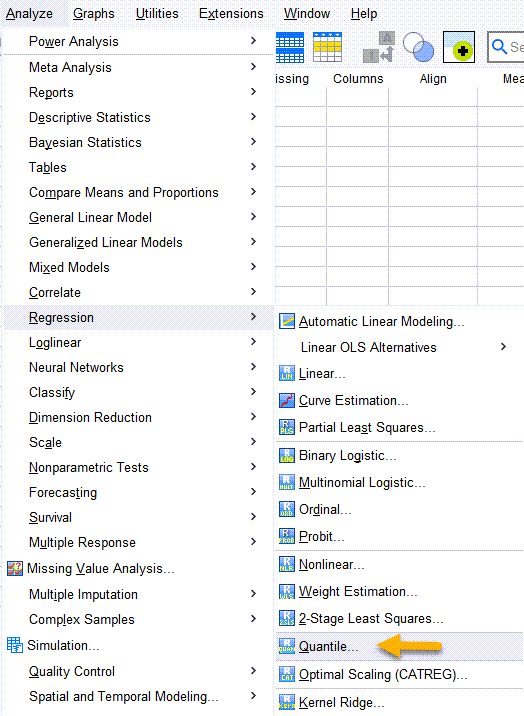
مسیر انجام تحلیل رگرسیون چندک در نرم افزار SPSS

تنظیمات نرم‌افزار در مدل Quantile

Setting

هنگامی که به مسیر بالا در نرم‌افزار SPSS می‌رویم، پنجره زیر با نام Quantile Analysis برای ما باز می‌شود.

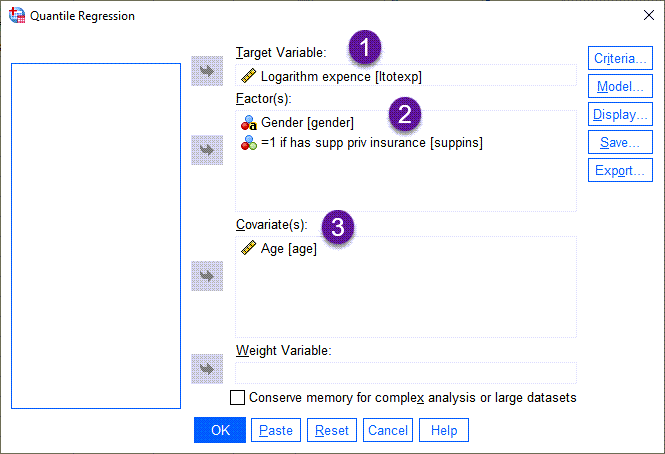
من هر کدام از بخش‌ها را با شماره قرار داده‌ام. به ترتیب هر یک را توضیح می‌دهم.

در بخش Target Variable همان ستون ltotexp که هزینه‌های پزشکی است و کمیت وابسته مطالعه را نشان می‌دهد، قرار می‌دهیم.
در بخش Factor(s) کمیت‌های جنسیت و داشتن بیمه تکمیلی که به صورت Variableهای اسمی هستند، قرار می‌گیرد.
Covariate و X این مطالعه، همان سن افراد است. بنابراین آن را در کادر Covariate قرار می‌دهیم. اگر مطالعه‌ای بیشتر از یک X‌ داشته باشد نیز ایرادی ندارد و در همین بخش قرار می‌گیرد.

Criteria

از آنجا که می‌خواهیم رابطه رگرسیونی بین چندک‌های شرطی (چارک اول q=0.25، میانه q=0.5 و چارک سوم q=0.75) هزینه‌های پزشکی و سن، وضعیت سلامت و بیمه تکمیلی را به دست بیاوریم، بنابراین بر روی تب بزنید. وارد پنجره زیر می‌شوید.

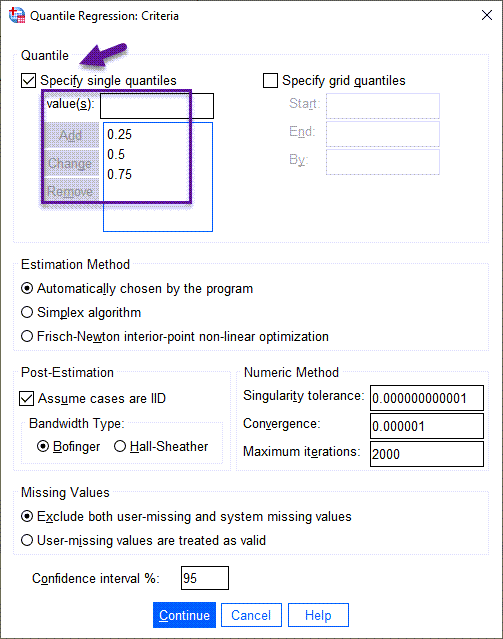
در پنجره Quantile Analysis Criteria گزینه Specify single quantiles را انتخاب کنید. از آن‌جا که می‌خواهیم چارک اول، میانه و چارک سوم را بررسی کنیم، بنابراین اعداد 0.25 و 0.5 و 0.75 را اضافه می‌کنیم.

با بقیه تنظیمات این پنجره کاری نداریم. یک نکته هم اینکه اگر بخواهیم برای یک محدوده و رنجی از چندک‌ها، رگرسیون به دست بیاوریم از گزینه Specify grid quantiles استفاده می‌کنیم.

Display

بر روی تب بزنید. در این پنجره می‌توانید علاوه بر خروجی‌ها و نتایجی که نرم‌افزار به صورت پیش‌فرض در رگرسیون چندک ارایه می‌دهد، یافته‌های بیشتری نیز داشته باشیم.

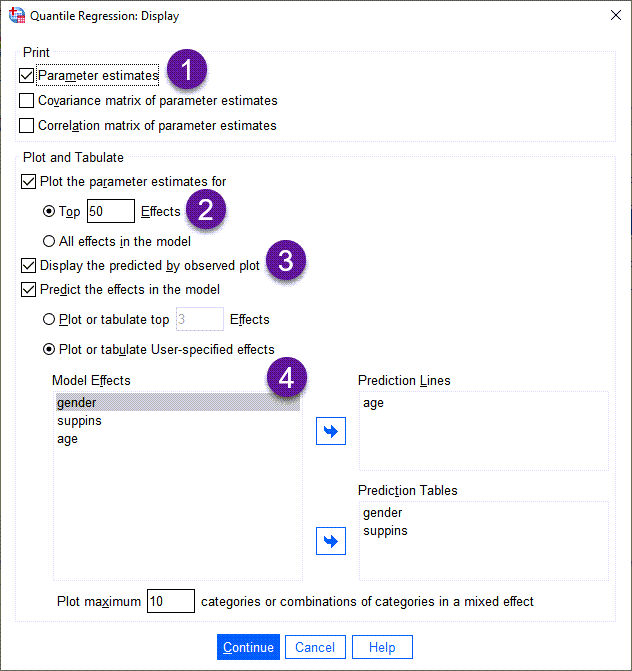
من هر کدام از بخش‌ها را با شماره قرار داده‌ام. به ترتیب هر یک را توضیح می‌دهم.

ابتدا گزینه Parameter estimates را انتخاب می‌کنیم. این کار باعث می‌شود ضرایب رگرسیونی مدل چندک برای ما نمایش داده شود.
در بخش Plot and Tabulate گزینه Plot of the Estimated Parameters را انتخاب می‌کنیم. این کار سبب می‌شود، گراف‌هایی با همین نام در خروجی نتایج، نشان داده شوند. بعداً و به هنگام بیان نتایج، بیشتر درباره‌ی آن‌ها صحبت می‌کنیم.
گزینه Display the predicted by observed plot را انتخاب می‌کنیم.
گزینه Plot or tabulate User-specified effects را انتخاب می‌کنیم. در Prediction Lines کمیت age و در Prediction Tables کمیت‌های gender و suppins را قرار می‌دهیم.

Save

بر روی تب بزنید. وارد پنجره زیر می‌شوید.

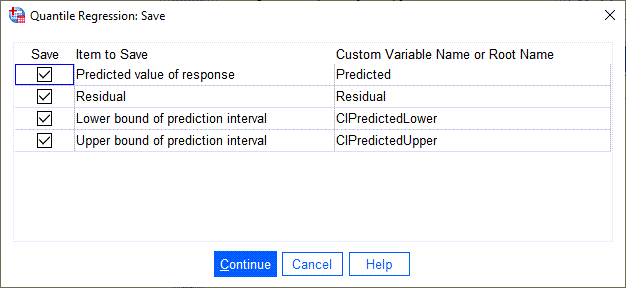
با انتخاب گزینه‌های این پنجره، ستون‌های جدیدی به فایل دیتا اضافه خواهند شد. این ستون‌‌ها اطلاعات بیشتری درباره‌ی مقادیر پاسخ پیش‌بینی شده و فواصل اطمینان آن به همراه باقیمانده‌های مدل رگرسیونی، نشان خواهند داد.

نتایج تحلیل رگرسیون چندک

Quantile Results

در ابتدای نتایج و خروجی‌های نرم‌افزار SPSS جدول Model Quality آمده است. تصویر آن را در ادامه می‌بینید.

از آنجا که از نرم‌افزار خواسته‌ایم برای چارک اول، میانه و چارک سوم هزینه‌های پزشکی، مدل رگرسیونی به آورد، بنابراین جدول Model Quality نیز برای این qها، آماره‌های مناسب بودن مدل یعنی شبه ضریب تعیین Pseudo R Squared و میانگین مطلق خطا Mean Absolute Error (MAE) را به دست آورده است.

همان‌گونه که می‌دانیم ضریب تعیین اندازه‌ای است که میزان پراکندگی‌های توضیح داده شده Y توسط X ها را بیان می‌کند. این عدد هر چقدر به یک نزدیکتر باشد، نشان‌دهنده بهتر بودن مدل است. میانگین مطلق خطا هم که به سادگی از رابطه $ \displaystyle MAE=\frac{{\sum\limits_{{i=1}}^{n}{{\left| {{{e}_{i}}} \right|}}}}{n}$ به دست می‌آید.

جدول Parameter Estimates by Different Quantiles در ادامه آمده است.

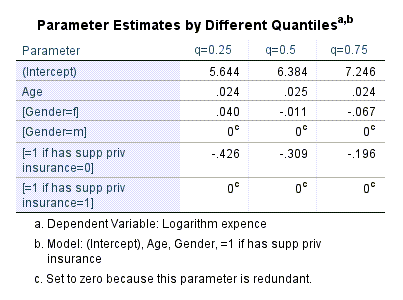
در این جدول ضرایب رگرسیونی مدل چندک به ازای هر کدام از qهای انتخابی، به دست آمده است. به عنوان مثال نتایج به دست آمده در جدول بالا نشان می‌دهد سن یک عامل تاثیرگزار مثبت بر هزینه‌های پزشکی است به این معنا که افزایش سن سبب افزایش هزینه‌های پزشکی می‌شود.

برای چارک اول یعنی q=0.25 زنان هزینه‌ةای پزشکی بیشتری پرداخت می‌کنند اما برای میانه و چارک سوم q=0.75 مردان هزینه‌های پزشکی بیشتری دارند.

در هر سه چارک نیز نداشتن بیمه‌های تکمیلی یعنی کد insurance=0 منجر به کمتر بودن هزینه‌های پزشکی شده است. این نتیجه را می‌توان از منفی بودن ضرایب رگرسیونی به دست آورد.

جدول Parameter Estimates نتایج بیشتری درباره رابطه بین X و Y در اختیار ما قرار می‌دهد. به عنوان مثال جدول براورد پارامترهای رگرسیون چندک برای میانه، نمایش داده شده است.

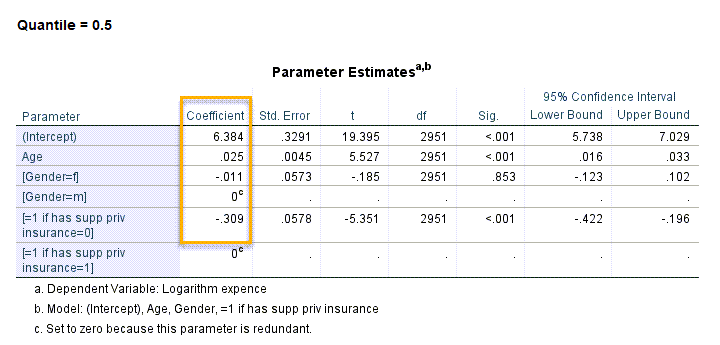
جدول Parameter Estimates برای میانه q=0.5

همان‌گونه که در این جدول مشاهده می‌کنید سن، مرد بودن و داشتن بیمه تکمیلی سبب افزایش میانه هزینه‌های پزشکی شده است. در این بین تاثیر سن و بیمه‌های تکمیلی، معنادار به دست می‌آید. اما جنسیت تاثیر معنادار ندارد (P-value=0.853). مقادیر احتمال و فواصل اطمینان 95 درصد برای ضرایب رگرسیونی را می‌توانید در جدول بالا مشاهده کنید.

در ادامه‌ی خروجی‌های نرم‌افزار، گراف‌هایی با عنوان Plot of the Estimated Parameters رسم شده است.

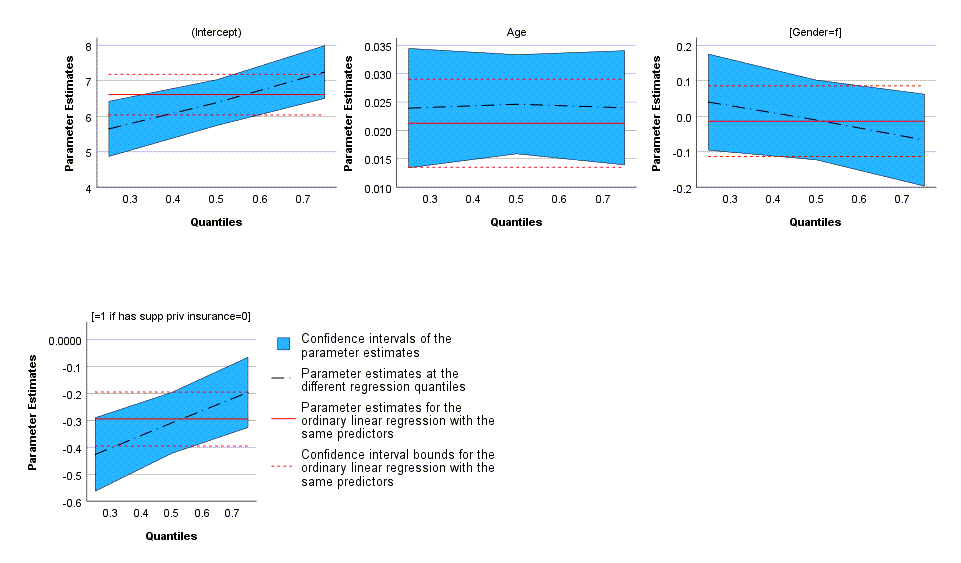
در این گراف‌ها به ازای هر کدام از Xهای مدل، ضرایب رگرسیون خطی معمولی همراه با فواصل اطمینان آن‌ها رسم شده است. خط قرمز و نقطه چین‌های قرمز رنگ را ببینید. چنانچه دقت کنید این خطوط ثابت و مستقیم هستند و به چندک‌ها Quantiles ذبطی ندارند.

به همین ترتیب ضرایب رگرسیونی در یک مدل چندک نیز به ازای هر کدام از Xها رسم شده است. این ضرایب وابسته به چندک‌ها هستند و با خط نقطه چین سیاه رنگ مشخص شده‌اند. همان‌گونه که می‌بینید این خطوط با کم یا زیاد شدن اعداد چندک در محور افقی، بالا یا پایین می‌روند.

به عنوان مثال برای جنسیت زنان، با افزایش چندک هزینه‌های پزشکی، تاثیر ضریب رگرسیونی f (زنان) کاهش پیدا می‌کند و برای q>0.5 حتی منفی نیز می‌شود.

این موضوع برای افرادی که فاقد بیمه تکمیلی هستند insurance=0 در گراف بالا آمده است. به این معنا که با افزایش چندک‌ها، تاثیر منفی عدم داشتن بیمه تکمیلی، کاهش پیدا می‌کند. البته همچنان منفی باقی می‌ماند و ضریب بتا بیمه، برای همه چندک‌ها منفی است.

سن نیز یک تاثیر تقریباً ثابت به ازای همه چندک‌های هزینه‌های پزشکی دارد و با افزایش و کاهش چندک‌ها، چندان بالا و پایین نمی‌شود.

یک نکته دیگر در این گراف‌ها، نواحی رنگی آبی است. این نواحی در واقع همان فواصل اطمینان برای ضرایب رگرسیونی مدل چندک هستند. آن‌ها کاملاً به خطوط نقطه چین سیاه، یعنی ضرایب رگرسیونی چندک وابسته هستند و از روی آن‌ها ساخته می‌شوند.

فهم و دقت در گراف‌های Estimated Parameters بسیار مهم است و آن‌ها را می‌توان از مهمترین خروجی‌های نرم‌افزار SPSS در تحلیل‌های Quantile Regression دانست.

معمولاً خطوط پیش‌بینی برای کمیت‌های کمکی Covariates ترسیم می‌شوند و جداول پیش‌بینی prediction tables برای فاکتورها ایجاد می‌شوند. در این مثال، Covariate همان Age است و فاکتورها gender و suppins در نظر گرفته شده‌اند.

در گراف زیر خطوط پیش‌بینی Prediction Lines برای سن، رسم شده است.

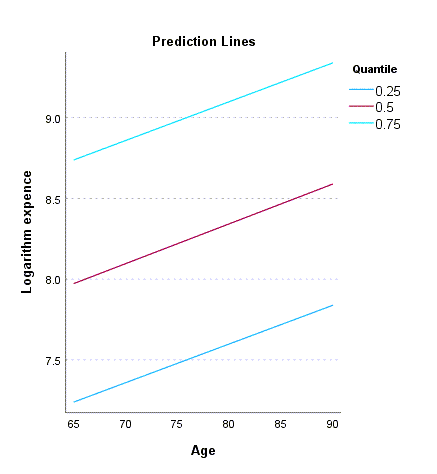
در این نمودار سن در برابر هزینه‌های پزشکی به ازای هر کدام از qهای انتخابی رسم شده است. همان‌گونه که از جدول Parameter Estimates by Different Quantiles نیز به دست آمد، ضرایب رگرسیونی برای همه چندک‌های انتخابی مثبت است. بنابراین خطوط پیش‌بینی در نمودار بالا صعودی به دست می‌آیند. به این مفهوم که افزایش سن، افزایش هزینه‌های پزشکی را در بر دارد.

به همین ترتیب در ادامه خروجی‌های نرم‌افزار، جداول پیش‌بینی prediction tables برای فاکتورهای مطالعه یعنی جنسیت و بیمه تکمیلی به دست آمده است.

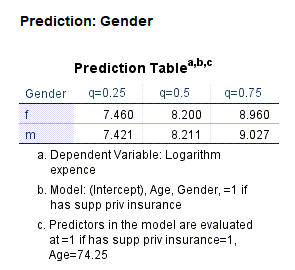
جدول پیش‌بینی بالا که برای فاکتور جنسیت به دست آمده است، برای هر کدام از چارک‌های اول، سوم و میانه و به تفکیک جنسیت، هزینه پزشکی مورد نیاز را پیش‌بینی کرده است. به عنوان مثال هزینه پزشکی میانه برای مردان 8.21 واحد و برای زنان 8.20 واحد به دست می‌آید.

نکته خوب است همین جا به یک نکته مهم اشاره کنیم. ما معمولاً عادت داریم به منظور مقایسه میانه در بین دو گروه مستقل از آزمون‌های ناپارامتری مانند من-ویتنی Mann-Whitney استفاده کنیم. صرفنظر از درست یا غلط بودن این موضوع، استفاده از یک رگرسیون چندک (میانه) کاربرد بسیار بهتری می‌تواند داشته باشد. به این مفهوم که بررسی کنیم آیا ضریب رگرسیونی (حاصل از مدل رگرسیون میانه) فاکتور گروه معنادار است یا خیر. اگر معنادار بود به این نتیجه می‌رسیم که میانه دو گروه با یکدیگر اختلاف معنادار دارد و اگر آن ضریب رگرسیونی معنادار ندارد، نتیجه می‌شود که میانه دو گروه با یکدیگر اختلاف معنادار ندارد.

به عنوان مثال در این مطالعه ما به این نتیجه می‌رسیم که میانه هزینه‌های پزشکی در مردان و زنان با یکدیگر اختلاف معنادار ندارد (بدون استفاده از آزمون ناپارامتری من-ویتنی). دلیل این مطلب نیز این است که در جدول Parameter Estimates ضریب رگرسیونی gender معنادار به دست نیامده است (P-value=0.853).

به همین ترتیب در خروجی‌های SPSS، جدول پیش بینی برای فاکتور بیمه تکمیلی نیز به دست آمده است. در تصویر زیر آن را ببینید.

در جدول پیش بینی بالا که برای بیمه‌های تکمیلی به دست آمده است، به ازای هر کدام از چارک‌های اول، سوم و میانه و به تفکیک داشتن یا نداشتن بیمه تکمیلی، هزینه پزشکی مورد نیاز را پیش‌بینی کرده است. به عنوان مثال هزینه پزشکی میانه برای افرادی که بیمه دارند 8.20 واحد و برای افرادی که بیمه ندارند 7.89 واحد به دست آمده است.

با توجه به نکته بالا، بیایید به یک سوال پاسخ دهید. آیا میانه هزینه‌های پزشکی برای افراد دارای بیمه و فاقد بیمه، با یکدیگر اختلاف معنادار دارد؟

پاسخ را می‌توانید با استفاده از جدول Parameter Estimates که برای q=0.5 به دست آمده، بیابید.

در پایان خروجی‌های نرم‌افزار، گراف Predicted by Observed رسم شده است. آن را ببینید.

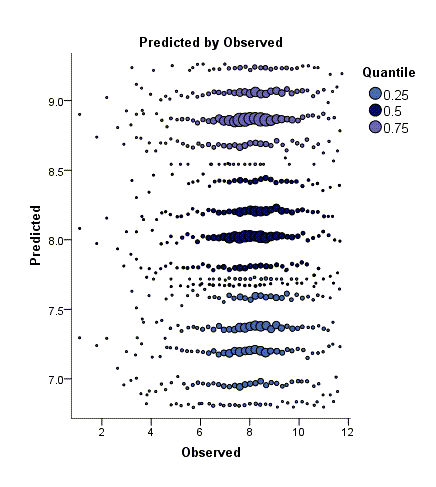
در این نمودار، مقادیر مشاهده شده Observed (محور افقی) هزینه‌های پزشکی در برابر مقادیر پیش‌بینی شده Predicted (محور عمودی) بر مبنای مدل رگرسیونی چندک، به دست آمده است. نتایج برحسب همان چندک‌های انتخابی ما، رسم شده است.

به خاطر داشته باشید ما در تب از نرم‌افزار خواستیم اطلاعات بیشتری درباره‌ی مقادیر پاسخ پیش‌بینی شده و فواصل اطمینان آن به همراه باقیمانده‌های مدل رگرسیونی، در اختیار ما قرار دهد. این نتایج در پنجره دیتا Data View قرار دارد. در تصویر زیر آن‌ها را ببینید.

Data View و اضافه شدن ستون‌های جدید پس از تحلیل رگرسیون چندک

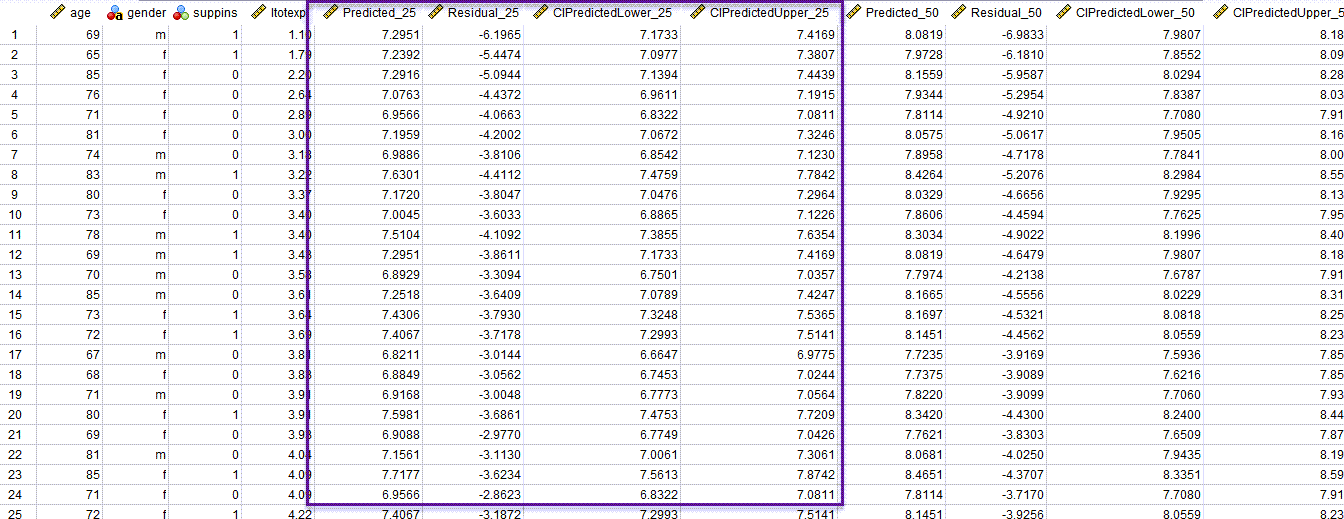
به عنوان مثال من در تصویر بالا، نتایج مربوط به q=0.25 را مشخص کرده‌ام. در این کادر، چهار ستون دیده می‌شود. یک ستون با نام Predicted_25 که عدد پیش‌بینی شده برای چارک اول هزینه‌های پزشکی به ازای هر فرد است. به عنوان مثال در سطر اول، عدد این ستون برابر با 7.2951 شده است. این عدد نشان می‌دهد، بر مبنای مدل رگرسیونی چندک، پیش‌بینی می‌شود، فرد سطر اول هزینه‌ای برابر با 7.2951 واحد پرداخت کند.

در ستون بعدی با نام Residual_25 مقدار خطای مدل به دست آمده است. خطای مدل از رابطه اختلاف بین مقدار واقعی و مقدار پیش بینی شده به دست می‌آید. این عدد برای فرد سطر اول برابر با -6.1965 به دست آمده است.

در ستون‌های بعدی با نام‌های CIPredictedLower_25 و CIPredictedUpper_25 به ترتیب کران پایین و کران بالای پیش بینی چارک اول هزینه‌های پزشکی، به دست آمده است. به عنوان مثال این اعداد برای فرد سطر اول به ترتیب برابر با 7.4169 و 8.0819 شده است.

در این مقاله به بیان و کاربرد مدل رگرسیون چندک Quantile Regression پرداختیم. براورد پارامترهای مدل، جداول آماری و گراف‌های به دست آمده در نرم‌افزار نیز در این مقاله توضیح داده شده است.

چگونه به این مقاله رفرنس دهیم

GraphPad Statistics (2022). Quantile Regression in SPSS Software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/Quantile-Regression-spss.php

For example, if you viewed this guide on 12^th January 2022, you would use the following reference

GraphPad Statistics (2022). Quantile Regression in SPSS Software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/Quantile-Regression-spss.php

ارایه خدمات تحلیل و مشاوره آماری

گراف پد برای شما خدمات مشاوره و انجام انواع تحلیل‌های آماری را ارایه می‌دهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.

سبد خرید