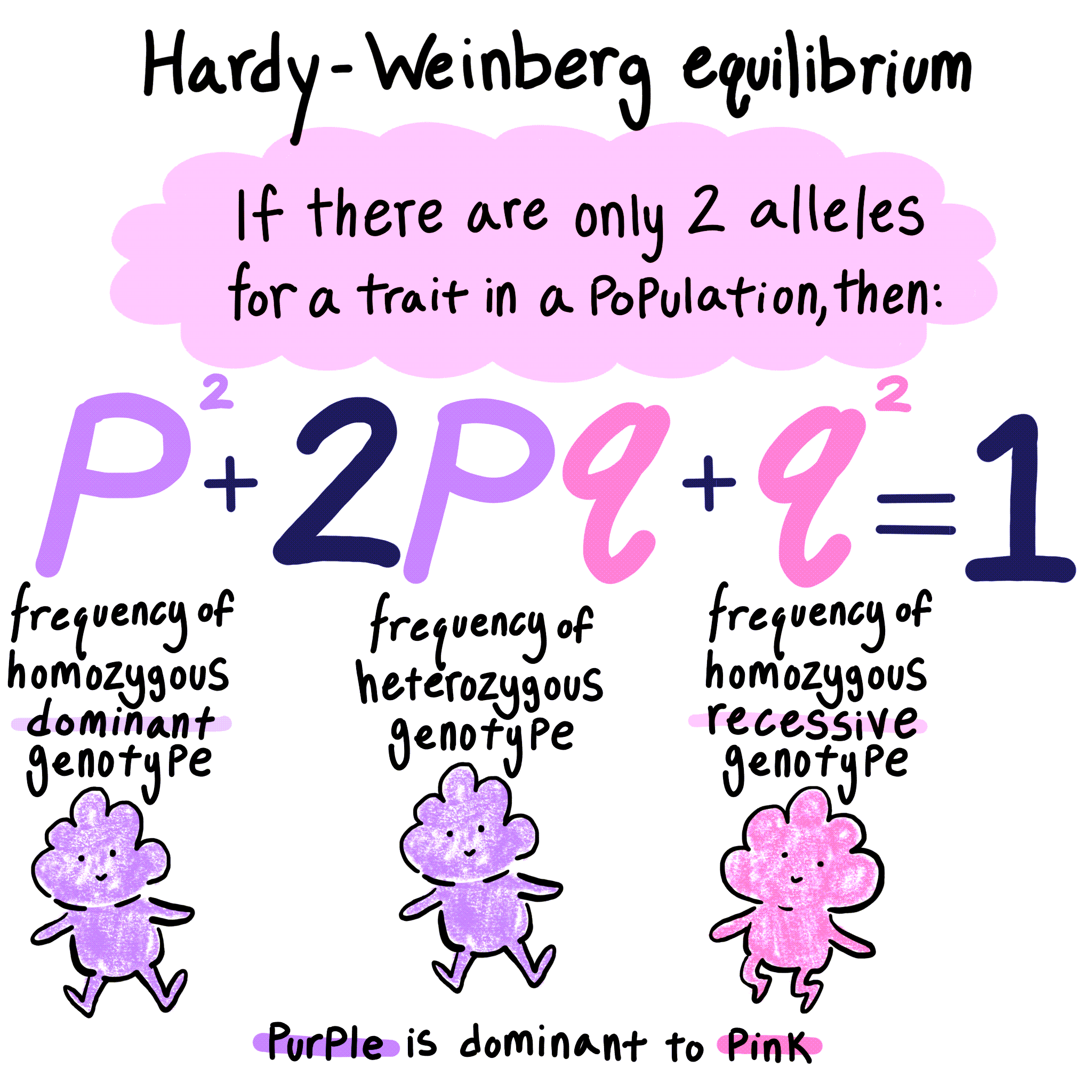طراحی نرمافزار تعادل هاردی وینبرگ
قانون تعادل هاردی وینبرگ (Hardy-Weinberg Equilibrium) که نتیجه مطالعات یک ریاضیدان انگلیسی و یک فیزیکدان آلمانی در سال 1908 است، بیان میکند فراوانی اللها و ژنوتیپ در یک جمعیت از نسلی به نسل دیگر در صورتی که عوامل مختل کننده از جمله جهش، انتخاب طبیعی، شارش ژن و جفت گیری غیرتصادفی رخ ندهد، در تعادل است و ثابت میماند. این قانون کاربرد فراوان در ژنتیک جمعیت دارد.
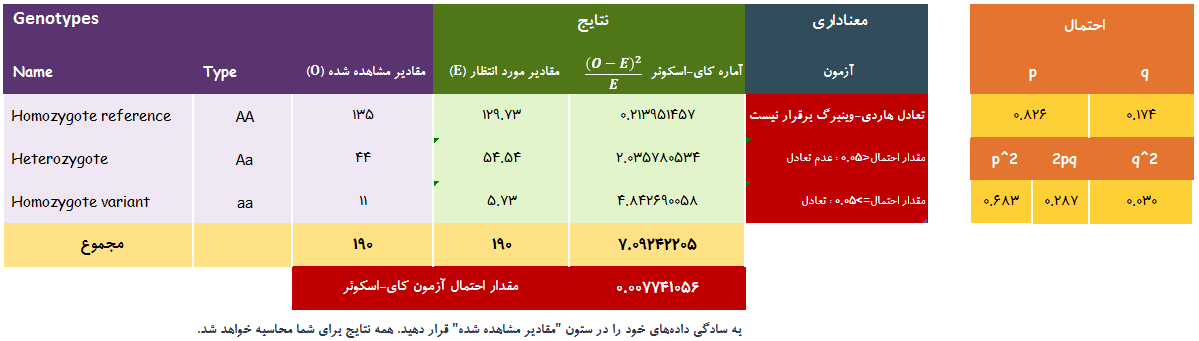
گراف پد برای اولین بار در کشور به طراحی نرمافزار تعادل هاردی-وینبرگ در دو فرمت فارسی و انگلیسی پرداخته است. به سادگی میتوانید نرمافزار را دریافت کرده و با وارد کردن اعداد مقاله و تحقیق خود، نتایج را به صورت کامل دریافت کنید. در ادامه همین صفحه چگونگی کار با نرمافزار در یک مثال آموزشی آمده است.