آنالیز واریانس یک طرفه One-way ANOVA با SPSS
آنالیز واریانس Analysis of Variance یا همان ANOVA یکی از مهمترین تحلیلهای آماری شناخته میشود.
در این نوشتار ما قصد داریم درباره آنالیز واریانس یک طرفه صحبت کنیم. این تحلیل هنگامی مورد استفاده قرار میگیرد که بخواهیم اعداد و اندازههای یک کمیت وابسته Dependent Variable را در بین گروههای مستقل یک فاکتور Factor مورد مقایسه قرار دهیم.
در شکل زیر میتوانید نحوه طراحی آنالیز واریانس یک طرفه را مشاهده کنید.
سوال
چرا میگوییم آنالیز واریانس یک طرفه؟
پاسخ ساده است. هنگامی که یک کمیت وابسته Dependent Variable با نام اختصاری D1 و تنها یک Factor با نام اختصاری F1 داشته باشیم، مطالعه ما از نوع آنالیز واریانس یک طرفه، خواهد بود.
در این متن، تحلیل آنالیز واریانس یک طرفه با استفاده از دو مسیر جداگانه و دو منوی متفاوت نرمافزار SPSS انجام خواهد شد. هر دو راهکار نتایج مشابهی خواهد داشت. یکی از این مسیرها استفاده از منوی Compare Means و دیگری روشهای با نام مدل خطی عام General Linear Model و یا همان GLM است. توصیه ما استفاده از تحلیلهای GLM است. در ادامه به هر دو روش خواهیم پرداخت.
نکته
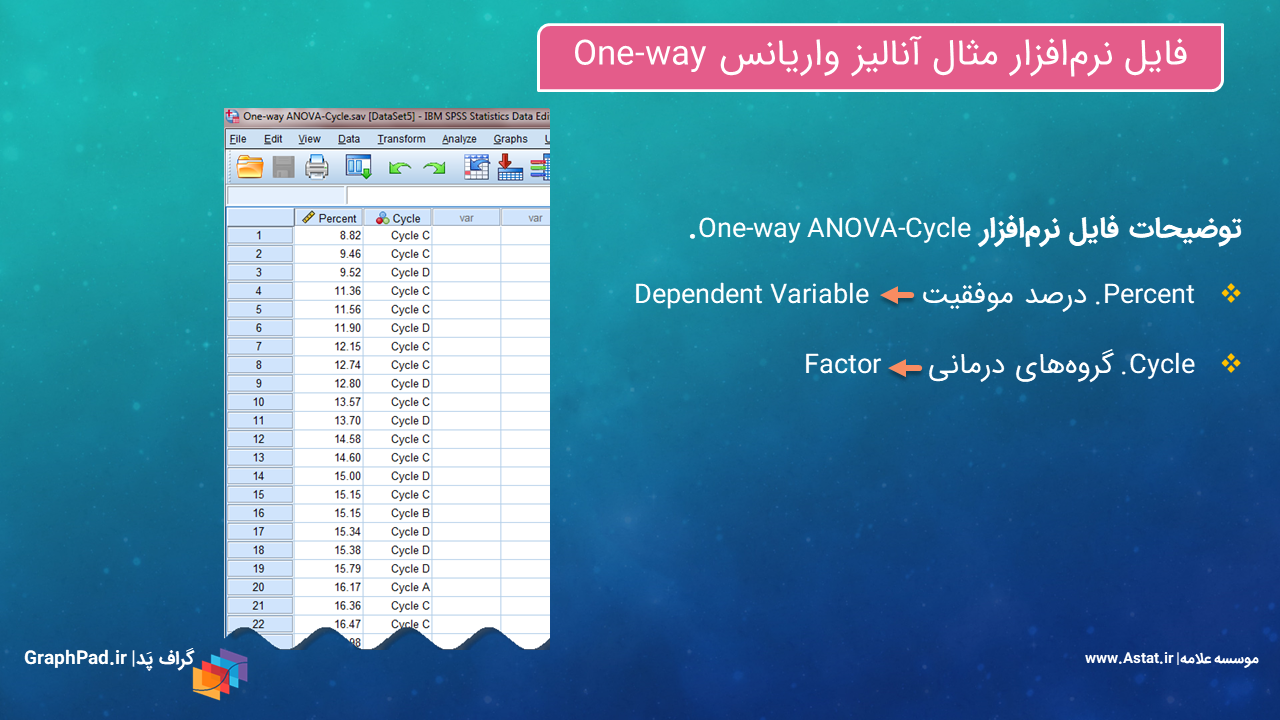
فایل دیتا و خروجی نرمافزار مثال را میتوانید از اینجا دانلود کنید. در تصویر زیر نیز توضیحاتی درباره فایل مثال آمده است.
همانگونه که در تصویر بالا مشاهده میکنید، میخواهیم درصد موفقیت را که در اینجا Dependent Variable به حساب میآید، در بین گروهها و سیکلهای مختلف درمان که Factor نامیده میشود، مورد مقایسه قرار دهیم.
به نحوه ورود دادهها به نرمافزار SPSS دقت کنید. در یک ستون با نام Percent، همه اعداد درصد موفقیت زیر هم نوشته میشود. Measure این ستون از نوع Scale است و همانگونه که بیان کردیم قرار است نقش Dependent Variable را بازی کند.
در ستون دیگر که در این مثال با نام Cycle است، به ازای هر درصد موفقیت، گروه درمانی آن آمده است. Measure این ستون میتواند از نوع Ordinal و یا Nominal باشد. این ستون نقش Factor را در یک مطالعه ANOVA خواهد داشت.
حال بیایید به ارایه و انجام One-way ANOVA جهت بررسی دادهها بپردازیم. در ابتدا جهت آنالیز واریانس یک طرفه، روش Compare Means را بیان میکنیم.
روش تحلیل ۱
One-way ANOVA with Compare Means
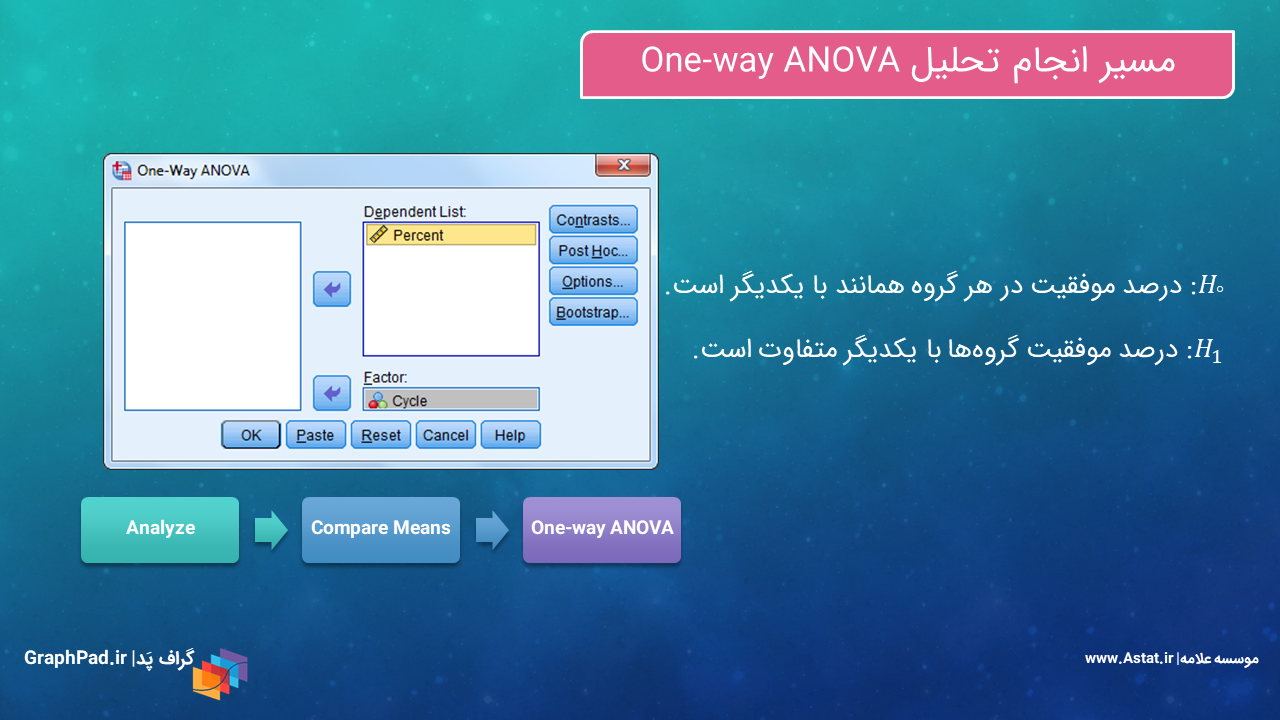
در تصویر زیر میتوانید فرضیات صفر و مقابل و همچنین مسیر آنالیز واریانس یک طرفه آن هم با استفاده از روش Compare Means را مشاهده کنید.
در تحلیل آنالیز واریانس یک طرفه، فرض صفر، برابری میانگین Dependent Variable در بین سطوح مختلف Factor است. در این مثال، فرض صفر به معنای این است که میانگین درصد موفقیت سیکلهای مختلف درمان با یکدیگر برابر است.
به همین ترتیب در تحلیل آنالیز واریانس یک طرفه، فرض مقابل، عدم برابری و وجود اختلاف میانگین Dependent Variable در بین سطوح مختلف Factor است. در این مثال، فرض مقابل به معنای این است که میانگین درصد موفقیت سیکلهای مختلف درمان با یکدیگر متفاوت است.
مسیر انجام آنالیز واریانس یک طرفه نیز هنگامی که میخواهیم از روش Compare Means استفاده کنیم، به صورت زیر خواهد بود.
مسیر نرمافزار
Analyze → Compare Means → One-way ANOVA
با رفتن به این مسیر، پنجره با نام One-Way ANOVA باز میشود. Percent را در کادر Dependent Variable و Cycle را در کادر Factor قرار میدهیم.
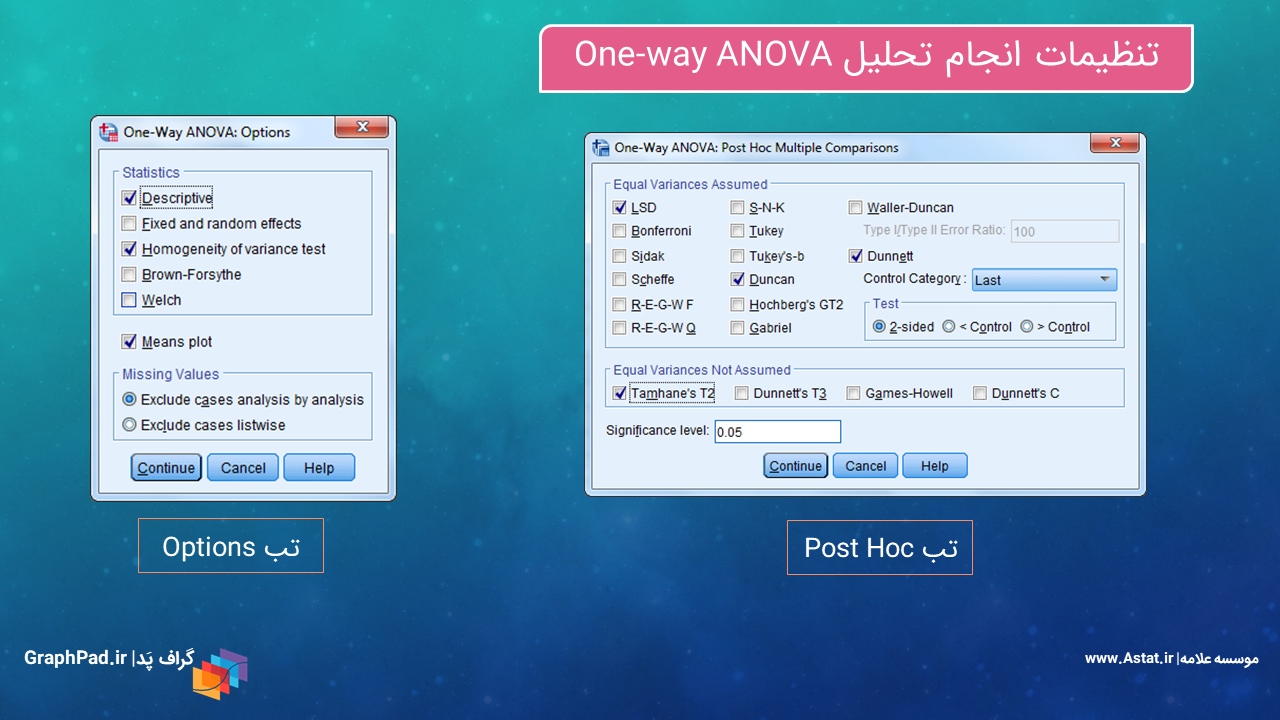
همچنین در تب Post Hoc و Options میتوانیم تنظیمات دلخواه خود را انتخاب کنیم. در تب Post Hoc انواع مقایسههای دوگانه بین گروههای مختلف Factor مشاهده میشود. با استفاده از این تب میتوانیم درصد موفقیت را بین هر دو سیکل دلخواه، با هم مقایسه کنیم. در تب Options نیز آمارههای توصیفی، آزمون همگنی واریانسها و رسم پلات میانگینها، قابل نمایش و انتخاب است.
حال OK میکنیم. در فایل Output نرمافزار SPSS نتایج و خروجیهای زیر به دست میآید. به ترتیب آنها را بیان میکنیم.
در جدول زیر که حاصل انتخاب گزینه Descriptive از تب Options است، انواع آمارههای توصیفی درصد موفقیت به ازای هر کدام از سیکلهای درمانی آمده است.
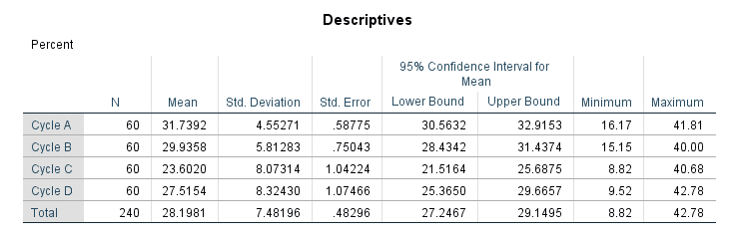
به عنوان مثال Cycle A دارای میانگین موفقیت ۳۱.۷۴ و انحراف معیار ۴.۵۵ است. نتایج مربوط به سایر سیکلها را نیز میتوانید مشاهده کنید.
آزمون همگنی واریانسها که در اینجا با نام لوین Levene انجام شده است، یافته دیگری است که به دلیل انتخاب گزینه Homogeneity of variance test در تب Options، به دست آمده است. این آزمون بررسی میکند که آیا واریانس درصد موفقیت گروههای مختلف Factor و در اینجا یعنی سیکلهای درمانی، با یکدیگر برابر هستند یا خیر.
در جدول زیر از خروجیهای نرمافزار SPSS میتوانید نتایج آزمون همگنی واریانسها را مشاهده کنید.
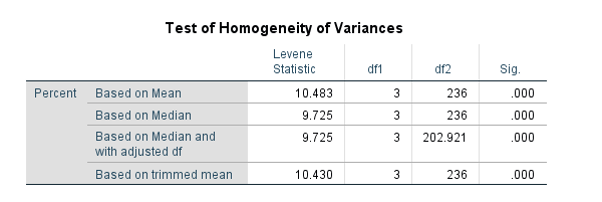
نتیجه به دست آمده بیانگر عدم همگن بودن واریانس درصد موفقیت در سیکلهای مختلف درمانی است (P-value < 0.001).
آزمون آنالیز واریانس بین گروهی و درون گروهی، عمومیترین نتیجه در انجام هر ANOVA به حساب میآید. در جدول زیر نتایج آن را مشاهده میکنید.
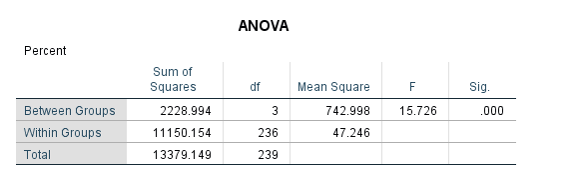
مجموع و میانگین مربعات،آماره F و مقدار احتمال P value آنالیز واریانس یک طرفه در این جدول بیان شده است. نتیجه به دست آمده به وضوح نشان میدهد درصد موفقیت بین گروههای Factor (سیکلهای درمانی) اختلاف معنادار وجود دارد (P-value < 0.001).
انجام مقایسههای جفتی بین هر کدام از گروههای Factor با یکدیگر، یافته مهمی است که در جدول زیر با نام Multiple Comparisons آمده است. این جدول به دلیل انتخاب گزینههای مختلف در تب Post Hoc به دست آمده است. به عنوان مثال ما آزمونهای LSD، Duncan، Dunnett و Tamhane’s T2 را انتخاب کرده بودیم.
نتایج جدول Multiple Comparisons به خوبی مقایسه بین سیکلهای درمانی را انجام داده است.
این مطلب که از کدام آزمون استفاده کنیم، بیشتر به این نتیجه برمیگردد که در آزمون لوین، همگنی واریانسها تایید شده است یا رد. از آنجا که در این مثال فرض همگن بودن واریانس درصد موفقیت در سیکلهای درمانی رد شده است، پس بهترین آزمون، گزینههای بخش پایینی تب Post Hoc است که مربوط به موارد رد فرضیه همگنی واریانسها است. آنها را میتوانید ببینید.

بنابراین در این مثال نتایج Multiple Comparisons مربوط به آزمون Tamhane’s T2 دقیقتر خواهد بود.
بر مبنای آزمون Tamhane’s T2 به دست میآوریم که درصد موفقیت سیکلهای درمانی A و B اختلاف معناداری با یکدیگر ندارند (P-value = 0.315). به همین ترتیب در سیکل B و D نیز تفاوت معنادار مشاهده نمیشود (P-value = 0.343). در سطح معناداری پنج درصد نیز بین درصد موفقیت سیکلهای C و D اختلاف معنادار دیده نمیشود (P-value = 0.059). با این حال با اغماض و یا بالا بردن اندک سطح معناداری، میتوان به وجود اختلاف در بین سیکلهای C و D اشاره کرد.
در آزمون دانکن Duncan نیز که نتایج آن را مشاهده میکنید، گروههای مختلف Factor در چند زیرمجموعه Subset قرار میگیرند. گروههای قرار گرفته در هر زیرمجموعه با هم اختلاف معنادار ندارند اما با گروههای سایر زیرمجموعهها اختلاف معنادار دارند.
در پایان نتایج، نمودار خطی میانگین درصد موفقیت به ازای هر گروه دیده میشود. این پلات به دلیل انتخاب گزینه Means plot در تب Options به دست آمده است.

همانگونه که مشاهده میکنید، سیکل C دارای کمترین میزان درصد موفقیت، نسبت به سایر سیکلهای درمانی است. با استفاده از آزمون دانکن به دست آوردیم که درصد موفقیت در این سیکل با سایر گروهها اختلاف معنادار دارد. سیکل A نیز با میانگین موفقیت 31.7 درصد، دارای بالاترین نتیجه عملکرد است.
خب، تا اینجا ما برای بیان آنالیز واریانس یک طرفه یا همان One-way ANOVA از روش Compare Means استفاده کردیم. در ابتدای بحث از روش دیگری با نام General Linear Models نام بردیم و بیان کردیم که این روش نسبت به Compare Means ارجحیت دارد. در ادامه روش GLM یا همان مدل خطی عام را مطرح میکنیم.
روش تحلیل ۲
General Linear Model , Univariate
مسیر انجام آنالیز واریانس یک طرفه نیز هنگامی که میخواهیم از روش General Linear Model استفاده کنیم، به صورت زیر خواهد بود.
مسیر نرمافزار
Analyze → General Linear Model → Univariate
در شکل زیر مسیر و نحوه قرار گرفتن ستون دادهها در نرمافزار SPSS جهت انجام آنالیز واریانس یک طرفه با استفاده از Univariate روش GLM آمده است.

با رفتن به این مسیر، پنجره با نام Univariate باز میشود. Percent را در کادر Dependent Variable و Cycle را در کادر Fixed Factor قرار میدهیم.
خوب است در همین جا این نکته را بیان کنیم که چنانچه در کادر Fixed Factor ستون و Variable دیگری نیز قرار بگیرد، آنگاه مطالعه ما آنالیز واریانس دوطرفه Two-way ANOVA خواهد بود. این مطلب را از این جهت بیان کردیم که یک مطالعه از نوع آنالیز واریانس دوطرفه نیز با استفاده از همین منوی Univariate انجام میشود. در نوشتههای بعدی به این بحث خواهیم پرداخت.
در پنجره Univariate تبهای مختلفی دیده میشود. در تب Post Hoc انواع مقایسههای دوگانه بین گروههای مختلف Factor مشاهده میشود. این بخش همانند روش Compare Means است که در بالا به آن اشاره کردیم. با استفاده از این تب میتوانیم درصد موفقیت را بین هر دو سیکل دلخواه، مقایسه کنیم. در تصویر زیر میتوانید انواع آزمونهای مقایسهای چندگانه برای میانگینهای مشاهده شده را ببینید.

به عنوان مثال آزمونهای بونفرونی Bonferroni و Tamhane’d T2 را انتخاب کردهایم.
در تب EM Means میتوانیم میانگینهای حاشیهای به ازای هر کدام از گروههای Factor را به دست آوریم. با انتخاب گزینه Compare main effects این میانگینهای حاشیهای قابل مقایسه با همدیگر هستند.
به همین ترتیب در تب Options آمارههای توصیفی، اندازه اثر effect size و توان power آزمون به همراه آزمونهای همگنی واریانسها را انتخاب میکنیم.
در تصویر زیر تنظیمات مربوط به تب EM Means و Options آمده است.

حال OK میکنیم. در فایل Output نرمافزار SPSS نتایج و خروجیهای زیر به دست میآید. به ترتیب آنها را بیان میکنیم. در تصویر زیر سه جدول ابتدایی نتایج را میتوانید مشاهده کنید.

در جدول Between-Subjects Factors اسامی گروههای Factor و تعداد هر گروه که برابر با ۶۰ مورد است، بیان شده است.
در جدول زیر که حاصل انتخاب گزینه Descriptive Statistics از تب Options است، انواع آمارههای توصیفی درصد موفقیت به ازای هر کدام از سیکلهای درمانی آمده است.
همچنین در جدول Levene’s Test of Equality of Error Variances آزمون لوین به منظور بررسی همگن بودن واریانس باقیماندههای مدل، آمده است. به این کلمه مدل دقت کنید. یک سوال دقیق میتواند این باشد،
سوال
کدام مدل؟ مگر ما قصد مقایسه Dependent Variable در سطوح مختلف Factor را نداریم؟ خب، این موضوع یک مبحث مقایسهای است و مدل یک موضوع رگرسیونی و ارتباط سنجی. این دو چه ارتباطی با هم دارند و چگونه میتوان از یک بررسی مقایسهای به مباحث مدلبندی و رگرسیونی رسید؟
موارد بالا سوالات بسیار دقیقی است و ما سعی میکنیم در ادامه به آنها پاسخ دهیم.
فعلاَ قدم به قدم پیش میرویم و اکنون در موضوع آزمون لوین و همگن بودن واریانس باقیماندهها هستیم. دربارهی اینکه با چه مدلی نیز روبهرو هستیم در ادامه توضیح خواهیم داد. به هر حال نتیجه آزمون لوین بیانگر عدم همگن بودن واریانس باقیماندههای مدل است (P-value < 0.001).
یادتان باشد در بالا و در روش Compare Means نیز به این نتیجه رسیدیم. رد شدن فرضیه همگنی واریانسها به ما در نحوه استفاده از آزمونهای Multiple Comparisons کمک خواهد کرد.
حال بیایید به بررسی نتایج جدول مهم Tests of Between-Subjects Effects بپردازیم. در شکل زیر برخی از توضیحات جدول آمده است. در ادامه بیشتر به آن میپردازیم.

در جداول Tests of Between-Subjects Effects آزمون معناداری فاکتورها، اثرات اصلی آنها Main Effect و در صورت وجود، اثرات متقابل Interaction Effect فاکتورها بررسی میشود. در این مثال و از آنجا که ما به موضوع آنالیز واریانس یک طرفه پرداختهایم، تنها یک Factor با نام Cycle داریم و اثر متقابل وجود دارد. در نوشتههای بعدی که به بررسی آنالیز واریانسهای چندگانه خواهیم پرداخت، به اثرات اصلی نیز اشاره خواهیم کرد.
نتیجه به دست آمده از جدول Tests of Between-Subjects Effects بالا بیانگر وجود تاثیر معنادار فاکتور Cycle بر Dependent Variable درصد موفقیت است (P-value < 0.001). اندازه اثر این فاکتور بر Dependent Variable برابر با ۰.۱۶۷ به دست میآید. توضیح اینکه Partial Eta Squared عددی بین صفر تا یک است و مقادیر نزدیک به یک آن نشاندهنده تاثیر بیشتر آن فاکتور بر کمیت پاسخ است.
ستونی نیز با نام Observed Power مشاهده میشود. این ستون که از آن با نام توان مشاهده شده نیز نام برده میشود، بیانگر میزان درستی رد فرض صفر است. همانگونه که میدانیم فرض صفر به معنای عدم معناداری و عدم تاثیرگزاری فاکتور بر روی کمیت پاسخ است. پس رد این فرضیه یعنی پذیرش معناداری و اثرگزاری. حال Observed Power بررسی میکند که رد این فرضیه چقدر درست است. توان نیز عددی بین صفر تا یک است و مقادیر نزدیک به یک به معنای درست بودن رد فرض صفر است.
در این مثال Observed Power برابر با یک به دست آمده است. به وضوح این عدد به معنای درست بودن رد فرض عدم معناداری و پذیرش معناداری است. به یک نکته اگر دقت کنید این است که Observed Power و Sig در خلاف جهت یکدیگر قرار دارند. یعنی اگر Sig بالا باشد، Power پایین به دست میآید و اگر Sig پایین باشد، Power بالا به دست میآید
در پایین جدول نیز متنی به صورت R Squared = .167 (Adjusted R Squared = .156) دیده میشود. چنانچه با مباحث رگرسیونی آشنا باشید این همان ضریب تعیین R Squared مدل رگرسیونی است. عدد ضریب تعیین نشان میدهد مدل به دست آمده چقدر میتواند کمیت پاسخ را توضیح دهد. در این مثال به معنای اینکه مدل شامل اثر اصلی Cycle چقدر میتواند Dependent Variable و یا همان درصد موفقیت را توضیح دهد. عدد برابر با ۰.۱۶۷ شده است. اگر دقت کنید این عدد همان عدد Partial Eta Squared در این مثال است. این مطلب نیز واضح است زیرا در این مدل فقط یک اثر اصلی داشتهایم و مطالعه ما آنالیز واریانس یک طرفه بوده است.
در بالا سوالی با عنوان کدام مدل؟ پرسیدیم و در اینجا داریم از مدل حرف میزنیم. خوب است حال به پاسخ این سوال بپردازیم و درباره مدل موجود در آنالیز واریانس یک طرفه هنگامی که از روش مدل خطی عام یعنی General Linear Model صحبت کنیم.
در ابتدا تصویر زیر را مشاهده کنید. در این تصویر مدل آماری One-way ANOVA هنگامی که از روش Univariate, GLM استفاده میکنیم، آمده است.
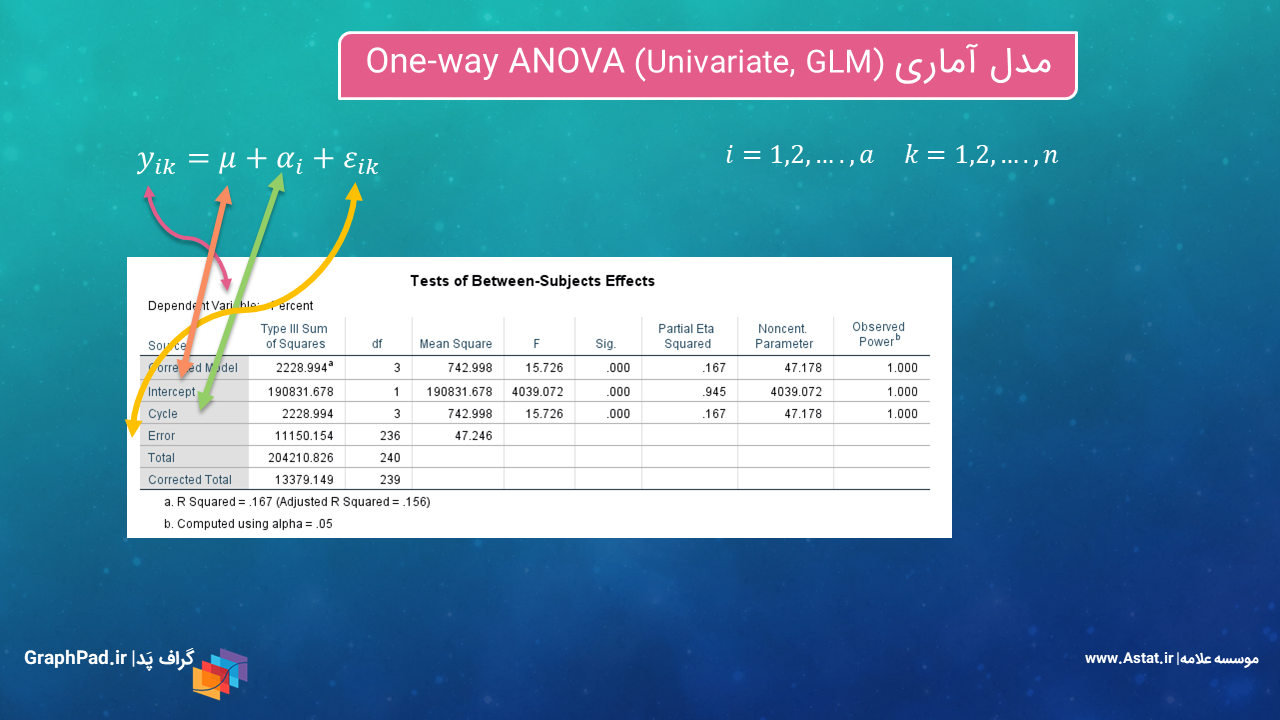
در واقع مدل خطی آنالیز واریانس یک طرفه به صورت زیر است.
yik = µ + αi + εik
در این مدل همانند همه مدلهای آماری دیگر میخواهیم با استفاده از یکسری کمیت مستقل Independent Variable اندازههای کمیت وابسته Dependent Variable را به دست بیاوریم و میزان تاثیر کمیتهای مستقل بر وابسته را مورد ارزیابی قرار دهیم.
در مدل بالا y همان کمیت وابسته Dependent Variable است که در این مثال درصد موفقیت بیان شده است. منظور از اندیس i گروه iام Factor و منظور از اندیس k نفر kام مورد بررسی است. مثلاَ وقتی مینویسیم y۱۵ یعنی درصد موفقیت نفر پنجم سیکل درمانی ۱ یا همان سیکل درمانی A.
بیایید برای فهم این مدل از μ شروع کنیم. همانگونه که در شکل بالا نشان داده شده است μ همان Intercept یا اثر ثابت مدل است. μ نشاندهنده این است که بدون در نظر گرفتن نوع سیکل درمانی، درصد موفقیت درمان چقدر خواهد بود. در جدول Tests of Between-Subjects Effects آزمون وجود اثر معنادار μ بر درصد موفقیت انجام شده است (P-value < 0.001). اندازه اثر μ نیز مقدار بالایی گزارش شده است (۰.۹۴۵ = η2).
اما αi چیست؟ α به معنای Factor مورد بررسی (در این مثال سیکل درمان) در مدل خطی است. . اندیس i هم بیانگر شماره و نوع سیکل درمان است. مثلاَ α۱ یعنی سیکل A و یا α۳ یعنی سیکل C.
در واقع در مدل خطی تحلیل واریانس یک طرفه، به دنبال پاسخ به این سوال هستیم که آیا α و یا همان Factor بر y یا همان کمیت وابسته Dependent Variable تاثیر معنادار دارد یا خیر.
به کلمه تاثیر دقت کنید. ما در آنالیز واریانس به دنبال مقایسه گروههای مختلف با یکدیگر هستیم. اگر دقت کرده باشید، در روش ابتدایی که در همین متن توضیح دادیم، نام آن Compare Means و مقایسه میانگینها بود. اما در روش General Linear Model میخواهیم به بررسی تاثیر Factor بر Dependent Variable بپردازیم.
این دو یعنی مقایسه گروههای Factor با یکدیگر در روش Compare Means و بررسی تاثیر Factor بر روی کمیت وابسته در روش GLM ، در امتداد و راستای یکدیگر هستند. در واقع هنگامی که بررسی میکنیم آیا Factor بر y اثر معنادار دارد یا خیر، به معنای این مفهوم است که آیا رفتار و عملکرد گروههای مختلف Factor در بررسی y با یکدیگر متفاوت است یا خیر.
به همین دلیل است که ANOVA در یک جا به مفهوم مقایسه بین گروههای Factor با یکدیگر است و در جای دیگر به معنای بررسی وجود تاثیر گروهها بر کمیت وابسته. چنانچه وجود این تاثیر، تایید شود به معنای این است که رفتار گروهها با یکدیگر متفاوت بوده و اگر وجود تاثیر، تایید نشود به معنای این است که رفتار گروهها با همدیگر همانند است.
مدل GLM همانند هر مدل آماری دیگری دارای خطا و باقیمانده است. در εik بخش خطا بیان شده است. در جدول Tests of Between-Subjects Effects نتایج این بخش با نام Error قرار میگیرد.
سطرهای دیگری نیز در جدول Tests of Between-Subjects Effects دیده میشود. در تصویر زیر درباره ارتباط بین این سطرها با مدل آماری GLM صحبت خواهیم کرد.
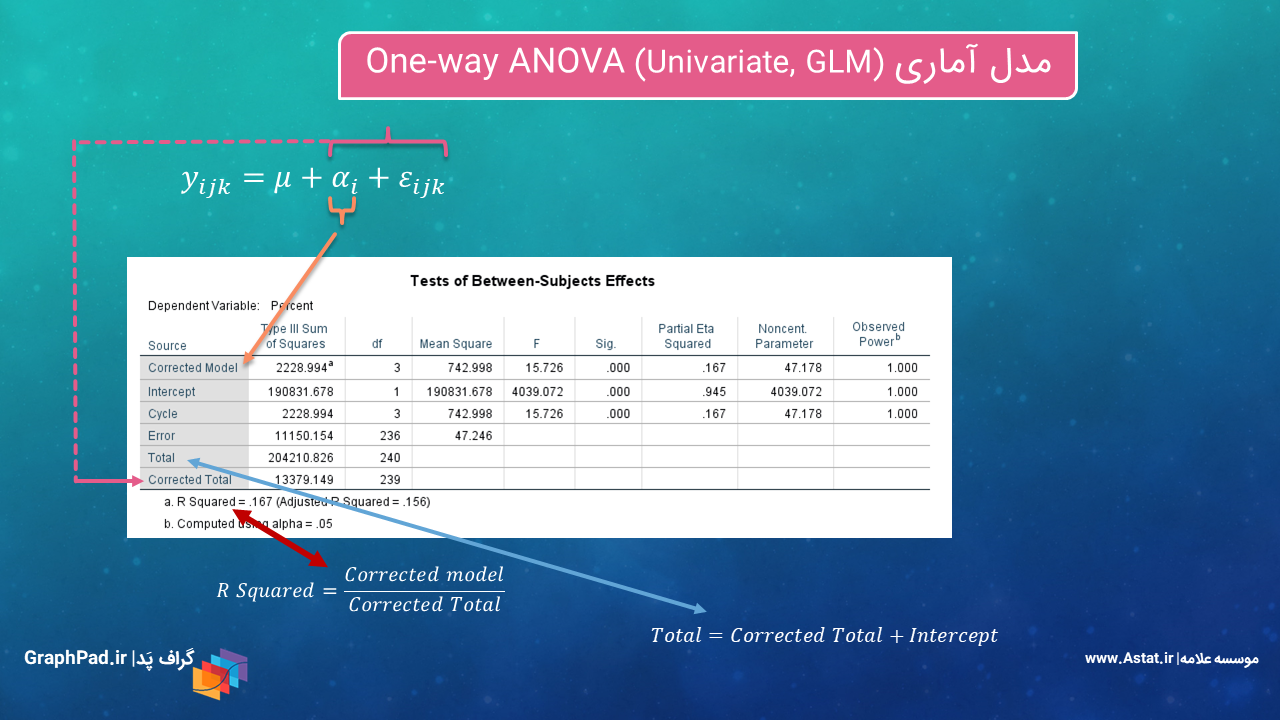
سطر Corrected Model یا مدل اصلاحشده، به فاکنورهای موجود در مدل اشاره میکند. از آنجا که این مثال ما آنالیز واریانس یک طرفه است، فقط یک فاکتور داشتیم که با نام Cycle در دادهها نامگزاری شده بود و در مدل با علامت αi آن را نشان دادیم. اگر در جدول Tests of Between-Subjects Effects دقت کنید، مقدار همه آمارههای Corrected Model مانند مجموع و میانگین مربعات، درجه آزادی، مقدار احتمال، اندازه اثر و توان، برابر با آمارههای فاکتور Cycle است. همانگونه نیز که گفتیم این مطلب طبیعی است زیرا فقط یک فاکتور در مدل One-Way ANOVA وجود دارد.
مجموع Corrected Model که در اینجا همان αi است و εik با نام Corrected Total نامیده میشود. چنانچه مجموع مربعات آنها را با هم جمع کتید به همان عدد مجموع مربعات Corrected Total میرسید.
سطر Total نیز به وضوح به مجموع Corrected Total (که خودش مجموع Corrected Model و Error بود) و Intercept اشاره میکند. در واقع مجموع مربعات Total ترکیب مجموع مربعات همه اجزای مدل شامل، اثر ثابت با نام μ، فاکتورهای موجود در مدل که در این مثال فقط αi بود و جمله خطا با نام εik است.
به همین ترتیب R Squared یا ضریب تعیین که آن را میزان توضیح مدل توسط فاکتورها مینامیم، به صورت Corrected Model نقسیم بر Corrected Total تعریف میکنیم. واضح است هر چقدر R Squared بیشتر باشد به معنای توضیح بهتر و بیشتر کمیت وابسته Dependent Variable (در این مثال درصد موفقیت) توسط فاکتورهای مدل است. برای بیشتر بودن ضریب تعیین باید جمله خطا و یا همان Error که در محرج فرمول ضریب تعیین قرار میگیرد باید کمتر باشد.
تا اینجا سعی کردم درباره تمام اجزا و محتویات جدول Tests of Between-Subjects Effects به دلیل اهمیت آن بپردازم. در تصویر زیر نتایج این جدول بار دیگر آمده است.
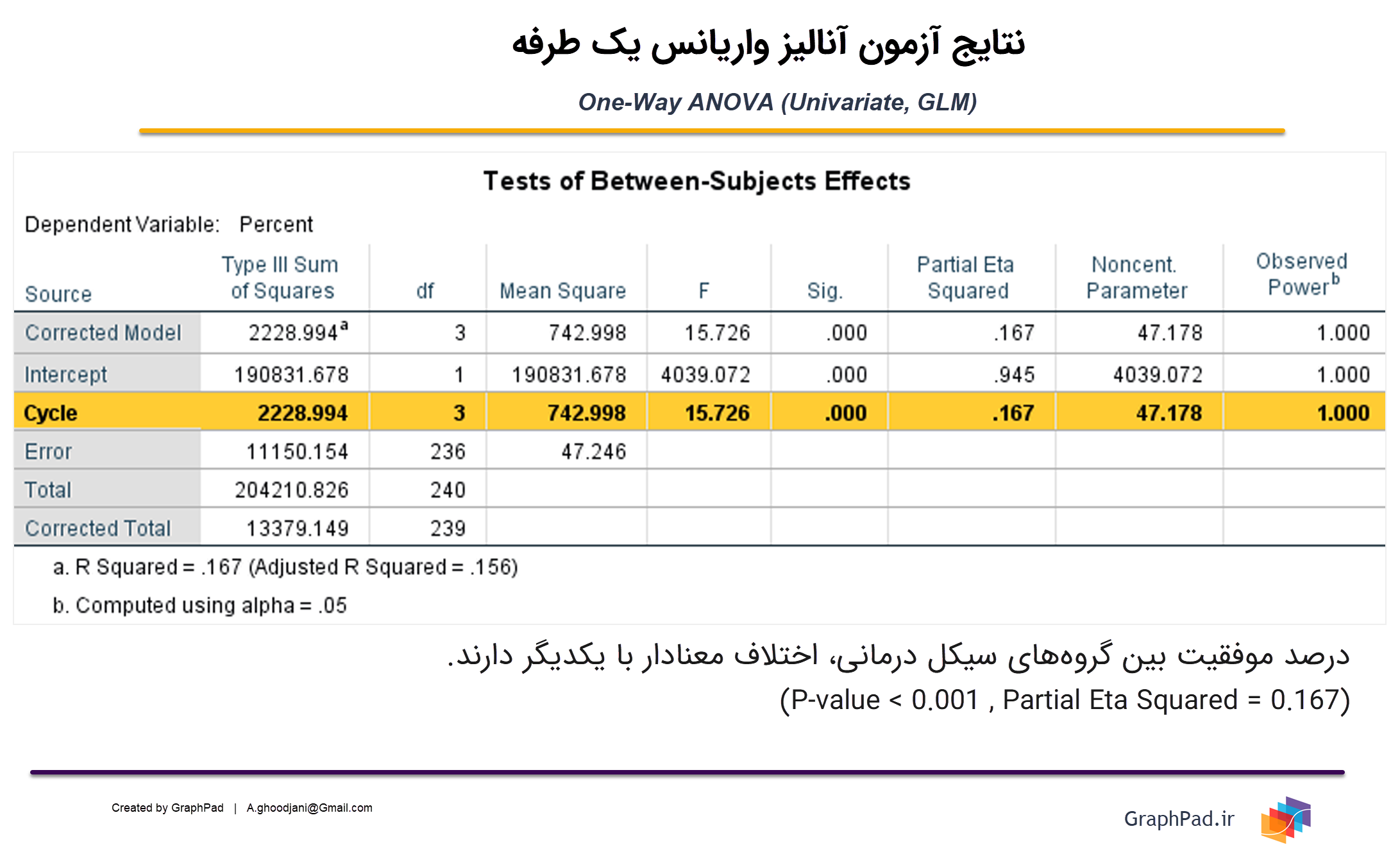
در ادامه درباره سایر خروجیهای نرمافزار در تحلیل One-way ANOVA (Univariate, GLM) صحبت میکنیم.
یادتان باشد در تنظیمات نرمافزار و در تب EM Means به دنبال آن بودیم که میانگینهای حاشیهای هر کدام از گروههای Factor را به دست آوریم. همچنین با انتخاب گزینه Compare main effects میانگینهای حاشیهای گروهها را با یکدیگر مقایسه کنیم. منظور از حاشیهای نیز این است که آمارههای توصیفی یک Factor را برحسب Factor دیگر به دست بیاوریم.
حال در ادامه خروجیهای نرمافزار، نتایج مربوط به تنظیمات تب EM Means آمده است.
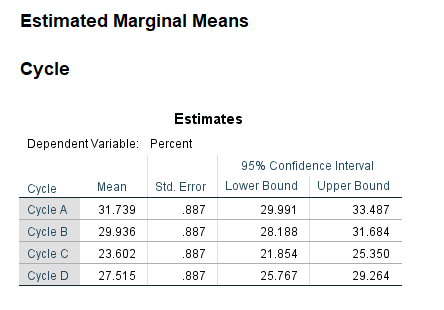
در این جدول آمارههای توصیفی حاشیهای Marginal مانند میانگین، خطای معیار و فواصل اطمینان ۹۵٪ برای درصد موفقیت به ازای هر کدام از سیکلها آمده است. به این نکته توجه کنید که از آنجا که تنها یک فاکتور داریم (مطالعه ما One-Way ANOVA است) میانگینهای حاشیهای برابر با میانگینهای حسابی است.
در تب EM Means با انتخاب گزینه Compare main effects از نرمافزار خواستیم که میانگینهای حاشیهای گروهها را نیز با یکدیگر مقایسه کند. این کار با استفاده از آزمون LSD انجام شده است. نتایج آن را میتوانید در شکل زیر مشاهده کنید.
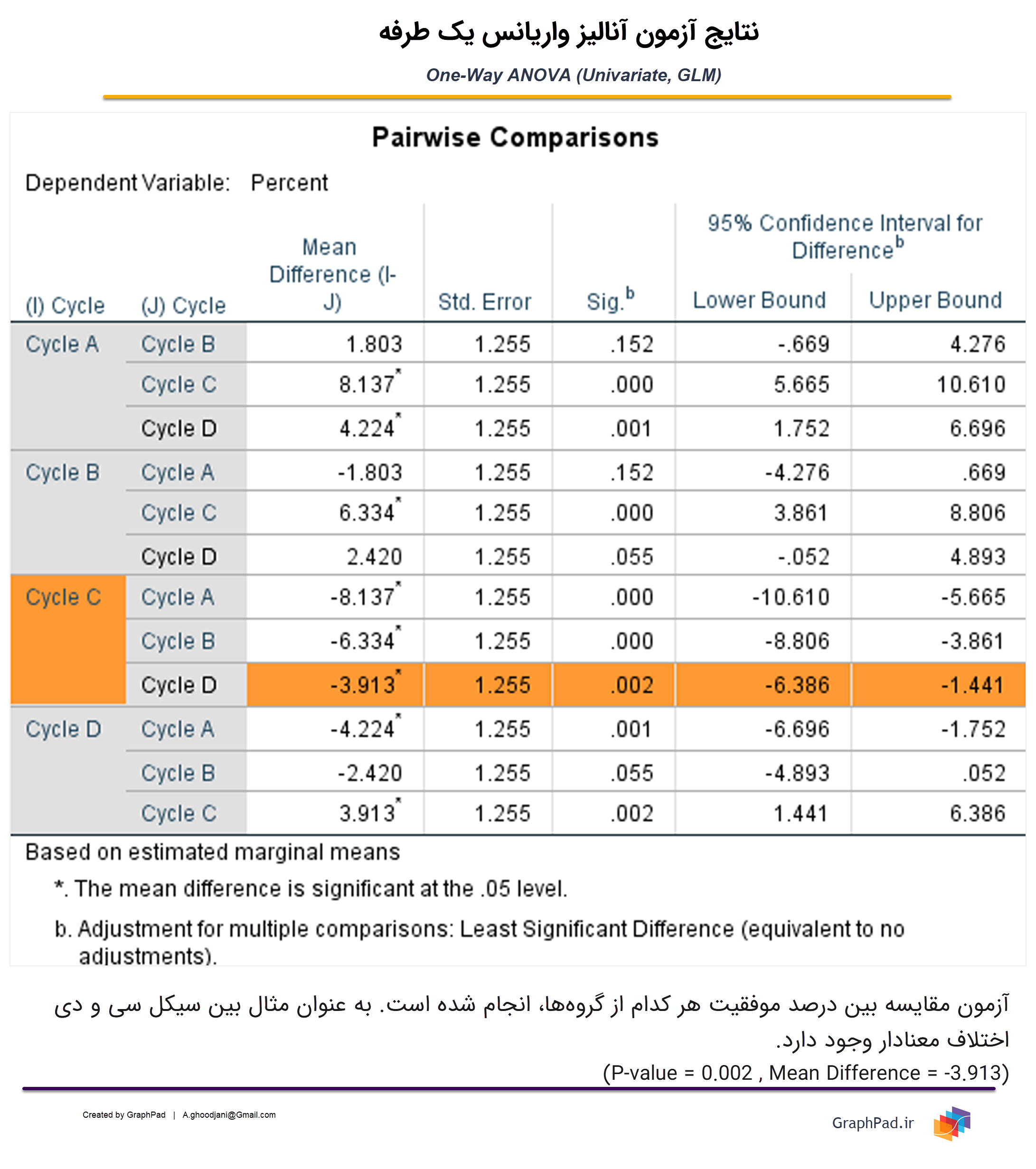
در جدول Pairwise Comparisons بالا که به مقایسه دو به دو میانگینهای حاشیهای گروههای مختلف فاکتور با یکدیگر پرداخته است، معناداری یا عدم معناداری این اختلافها به دست آمده است.
در ادامه خروجیهای نرمافزار جدول دیگری با نام Univariate Tests دیده میشود.

در این جدول دو سطر با نامهای Contrast و Error وجود دارد. منظور از Error همان جمله خطا در مدل خطی آنالیز واریانس یک طرفه است که در متنهای بالاتر به آن اشاره شد. چنانچه دقت کتید آمارههای مربوط به این سطر دقیقاَ برابر با آمارههای سطر Error در جدول Tests of Between-Subjects Effects است.
سطر Contrast نیز به فاکتورهای موجود در مدل خطی اشاره میکند. همانگونه که قبلاَ نیز گفتیم از آنجا که مثال ما آنالیز واریانس یک طرفه است بنابراین در اینجا فقط یک فاکتور با نام Cycle داریم. بنابراین آمارهها و نتایج مربوط به Contrast دقیقاَ برابر با نتایج سطر Cycle و همچنین Corrected Model است. در بالا نیز درباره این نتایج صحبت کردیم که بار دیگر تکرار نمیکنیم. تنها نکته اینکه از آنجا که ما در خروجیهای بخش Estimated Marginal Means هستیم، این نتایج و جدولها به همان دادههای میانگینهای حاشیهای مربوط است.
در تنظیمات انجام One-way ANOVA و در تب Post Hoc به عنوان مثال آزمونهای بونفرونی Bonferroni و Tamhane’d T2 را انتخاب کردیم. همانگونه که میدانیم با استفاده از این آزمونها میتوانیم به مقایسه دو به دو درصد موفقیت در بین گروههای Factor بپردازیم.
در ادامه خروجیهای نرمافزار SPSS نتایج مربوط به این تنظیمات با نام Multiple Comparisons آمده است. به این نکته نیز توجه کنید که نتایج این بخش بر روی میانگینهای حسابی خود گروهها است و مانند بخش قبل بر مبنای میانگینهای حاشیهای نیست. البته بار دیگر این نکته را تاکید میکنم، به دلیل اینکه مثال ما آنالیز واریانس یک طرفه است، بنابراین میانگینهای حاشیهای با میانگینهای حسابی برابر است.
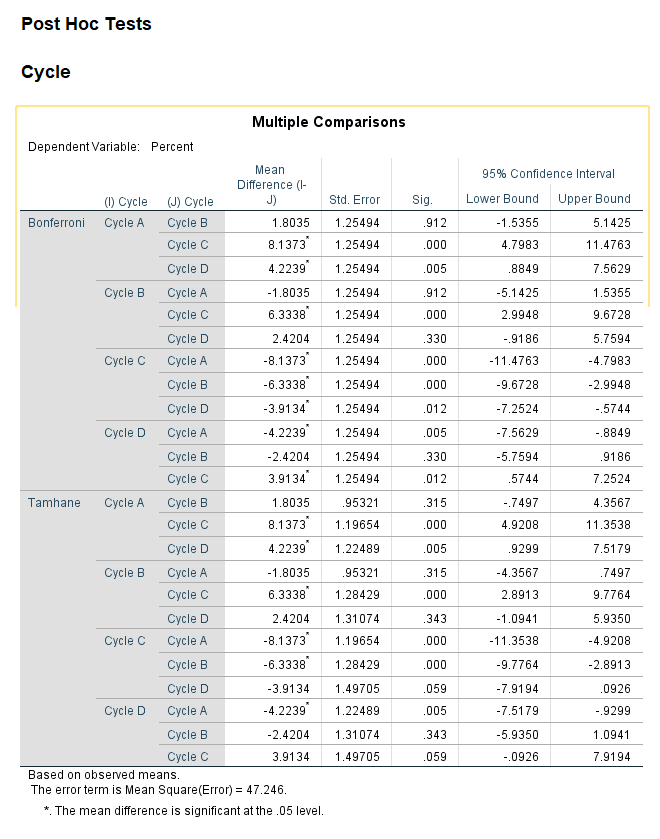
پاسخ به این سوال که از کدام آزمون بهتر است استفاده کنیم، در نتیجه جدول Levene’s Test of Equality of Error Variances یا همان آزمون لوین به منظور بررسی همگن بودن واریانس باقیماندههای مدل، قرار دارد. از آنجا که فرض همگنی واریانسها رد شده است بنابراین استفاده از آزمونهای بر مبنای رد فرضیه همگنی واریانسها در اولویت قرار دارد. از آنجا که آزمون Tamhane’d T2 بر مبنای رد فرضیه همگنی است، پس نتایج آن دقیقتر از نتایج آزمون بونفرونی خواهد بود.
خب، این هم از توضیحات روش آنالیز واریانس یک طرفه که با استفاده از روش Compare Means و General Linear Model , Univariate در نرم افزار SPSS به آن پرداختیم.
چگونه به این مقاله رفرنس دهیم
GraphPad Statistics (2020). One-way ANOVA with SPSS Software. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://graphpad.ir/general-linear-models-univariate-one-way-anova-spss/.php
For example, if you viewed this guide on 12th January 2022, you would use the following reference
GraphPad Statistics (2020). One-way ANOVA with SPSS Software. Statistical tutorials and software guides. Retrieved January, 12, 2022, from https://graphpad.ir/general-linear-models-univariate-one-way-anova-spss/.php
ارایه خدمات تحلیل و مشاوره آماری
گراف پد برای شما خدمات مشاوره و انجام انواع تحلیلهای آماری را ارایه میدهد. جهت دریافت نکات بیشتر بهتر است با ما تماس بگیرید.